基于乘客需求数据的定制商务班车站点选址方法

孙悦, 宋瑞，邱果

(北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

定制商务班车(customized business bus, CBB)的概念源于定制公交(subscription bus)，定制公交是根据乘客个性化需求，以多人共用车辆的形式设定线路，为出行起终点、出行时间、服务水平需求相似的人群提供量身定制的客运服务方式[1]。定制商务班车是依托互联网平台，由乘客在平台上提交通勤出行需求，运营方根据这些需求设计乘客上下班线路，并利用平台招募乘客、预订座位、在线支付的一种公交服务方式[2]。定制商务班车既继承了定制公交对乘客需求进行聚合的基本特征，同时又依托互联网平台，服务对象更集中于通勤乘客。

在常规公交站点选址问题的研究上，国内外学者已取得了较多的成果。叶英杰[3]把空间co-location模式挖掘技术应用在城市公交站点选址分布的研究当中。Saka[4]得出公交站点站间距的最优设置可以通过最小化公交车服务数量降低运营成本。Chien等[5]以总费用效益函数最小为目标优化了公交站点的数量和布局。Ziari等[6]提出了一种优化公交站点选址问题的新方法，并对总出行时间、选取速度等参数进行了灵敏度分析。Alonso等[7]研究了在不同拥挤程度网络的条件下，用双层优化模型求解公交站点的最佳位置。上层目标效益函数为社会费用最小，下层包括方式划分分配模型。Moura等[8]用两阶段模型分析了公交车站的最优位置，第一阶段以网络的社会费用最低为目标，从战略层面确定公交站点宏观的位置；第二阶段以公交服务的运营速度最大为目标，从战术层面获取特定线路站点的微观位置。

定制商务班车的站点选址问题是根据出行需求中乘客的居住点、工作点的地理位置，结合基础道路网等情况，对停靠站点进行选址的过程[1]。郭戎格[9]依据公交IC卡数据，运用OD站点识别算法等手段进行乘客出行空间特征分析研究。邹彦雯[1]通过改进K-means聚类算法，提出了IKCBB聚类算法用于对定制商务班车的站点选址问题进行求解。Kim等[10]在对站点选址的研究中建立了以乘客总出行距离最短和均衡每位乘客出行距离的班车站点设置模型。Shaffiei等[11]在一般的车辆路径问题中引入时间成本的概念，对原有站点进行合并或者加入新的站点。Cipriani等[12]分析了罗马市为代表的大型城市公交站点布设问题，开发了一种解决多对多的乘客出行需求的新算法。Nikolic等[13]将基于群体智慧的蜂群算法用于解决定制公交站点规划的组合优化问题。

不同于常规公交，定制商务班车更加重视对乘客需求数据的搜集、处理与分析。但现有研究使用的聚类算法较单一，主要以改进的K-means算法为主，而K-means算法需要提前指定聚类组号且无法规避噪声点的影响，聚类质量较差。同时，现有的研究对于如何在完成初步聚类后结合周围区位和出行条件因地制宜地进行选址探讨不多，研究的实践性不强。

为更好地解决定制商务班车选址问题，本文采用了基于密度的带有噪声的空间聚类(density-based spatial clustering of applications with noise, DBSCAN)算法来规避噪声点的影响和进行聚类组别的指定，同时为了体现定制商务班车精细化服务的特征，引入精细化指标指导聚类迭代，并结合区位和节点重要度思想对站点选址做出改进，增加了研究的实践性。

1 DBSCAN算法

1.1 相关定义

在DBSCAN算法中[14]，任意样本点N的ε邻域指以该点为中心，半径为Eps的区域，即图中以任意点为圆心，以长度为Eps的实线箭头为半径绘制得到的各种圆圈，如图1所示。

图1 DBSCAN算法概念Fig. 1 DBSCAN algorithm concept diagram

若样本点M的ε邻域内包含的样本点数大于等于最小包含点个数minPts, 则M为核心点。图1是以minPts=3来绘制的，图中以圆点为圆心的圆圈所包含的样本点数均达到这一阈值，所以图中圆点均为核心点。

图中五边形点和三角形点均为非核心点，其ε邻域包含的样本点数均未达到minPts的个数要求。其中五边形点为边界点，三角形点为噪声点，二者的区别方式取决于该点是否能从核心点密度可达。密度可达是DBSCAN算法用于说明样本间紧密联系程度的概念，由密度直达的概念引出。

密度直达如图中点Q与点M的关系所示，点Q位于点M的ε邻域内，而点M是核心点，所以点Q从点M密度直达，在图中用虚线箭头表示。而点M位于点P的ε邻域内，所以，点M从点P密度直达。因此点Q和点P以点M为桥梁建立了联系，这种联系在DBSCAN算法中被称为密度可达。

密度可达的关系如图中O、U、V、R所示，由于U、V之间密度直达，因而点R可从点O密度可达，而此时U、V都为核心点，故密度可达可以进行传递，点S从点O密度可达，故点R和点S密度相连。

在站点选址问题的实际应用中，扫描半径可代表行人距离定制商务班车的步行路径，最小包含点个数可代表满足定制商务班车的上车人数，密度直达点代表满足定制商务班车设站要求的一群乘客，而密度可达点表示这一类乘客的步行距离较近，可以视为集群分布。

1.2 DBSCAN聚类算法的流程

已知Dw为D中未被聚类点的集合，k为聚类别数，初始状态下令Dw=D，k=0, DBSCAN算法的主要执行步骤[15]可描述为：

步骤1：任意选择Dw中的一个点xj。若xj为非核心点，则执行步骤2；若xj为核心点，则执行步骤3。

步骤2: 将xj标记为噪声点，并从集合Dw中删除xj，注意此处仅在集合Dw中删除xj，xj仍在集合D中，仍可被其他核心点扫描到并划分到相应类簇。

步骤3：令k=k+1，确定D中所有与xj密度可达的点，并把xj及其密度可达点划分到类Ck中，并将Ck中的点从集合Dw中删除。

步骤4：若Dw中仍存在点未进行考察，则重复执行步骤1～3，直到Dw中的点被考察完毕为止。

由此可见，DBSCAN算法通过计算样本点间的紧密联系程度，找到密度相连点的最大集合并将其划分为一类，不同的密度相连集合构成了最终的聚类结果[16]。因此，DBSCAN算法能够识别噪声点，有效地防止了离散程度较大的样本点对聚类结果的影响。同时DBSCAN算法根据密度相连关系自动生成类别，可以根据数据特征生成类别而不需要指定聚类数，对数据的适应性强。但如果数据的密度分布较不均匀，聚类间距较大时，DBSCAN算法的聚类质量会显著降低。DBSCAN算法的聚类参数Eps及minPts往往根据经验选取，如果选择不合理对整体的聚类效果影响很大。由于定制商务班车的选址需要输出建议选址地点，这就要求DBSCAN算法不仅要输出类簇划分，还要生成聚类中心，这是基本的DBSCAN聚类算法不具备的。

2 改进的DBSCAN算法

2.1 改进的DBSCAN算法设计

2.1.1 精细化程度的衡量

基本的DBSCAN聚类算法可根据样本集合中各样本点的距离来进行划分，距离的度量采用欧氏距离的方式，因而该算法可以根据给定的聚类参数Eps和minPts确定聚类个数而不需要提前指定所需的聚类数。但在定制商务班车选址问题的实际应用中，聚类所得的各类簇包含的样本点个数不同，所处的城市区位不尽相同，有的类簇包含的样本点数量多且分布较广，出行客流量较大，需要进一步甄别出行需求，增设站点贯彻定制商务班车精细化服务的理念[17]。而有的类簇包含的样本点数量少且分布集中，出行客流量较少，本着节约成本的原则不需要再进一步设站。鉴于此，本文在基本DBSCAN聚类算法的基础上提出了类簇精细化判别步骤，根据类簇内样本点离散程度、类簇间客流的出行量和出行距离计算精细服务指数，对各类簇的精细化程度进行判断并分而治之。

2.1.1.1 类簇内离散程度分析

在对划分的类簇进行相应的公交站设置时，如果类簇内的样本点间距较远，证明其对应的乘客对上车站点的要求彼此距离较大，站点设置较少会增大乘客的步行距离，无法体现定制商务班车门对门服务的优势，因而有对类簇进行精细化划分的需要。为了衡量类簇的离散程度，采用误差平方和作为标准测度函数，使所获得的聚类本身尽可能地紧凑，而各聚类尽可能地分开。采用的误差平方和具体定义如下：

(1)

式中：αSSECp为类簇Cp中任意需求点到其他需求点的误差平方和的最大值；xj为类簇Cp中的任意需求点；cpcen为类簇Cp的质心；‖·‖为欧氏距离。

2.1.1.2 类簇间重要度分析

在城市区位理论中，若一个小区到其他小区的客流出行量较大，出行距离较短，证明该小区的区位重要度高，往往对应着大型商业圈，居民区等，而这些区域正是定制商务班车服务的起始点，因此能够正确地识别区位重要度对设置定制商务班车站点有十分重要的意义[18]。本文引入区位重要度的理念，将类簇视为区位重要度中的单元小区，根据各类簇间的客流量和出行距离分别计算类簇的重要度并进行比较，优先对区位重要度较高的类簇进行精细化服务。

在计算类簇重要度时，对于DBSCAN算法得到的类簇集，计算各类簇间客流量矩阵A：

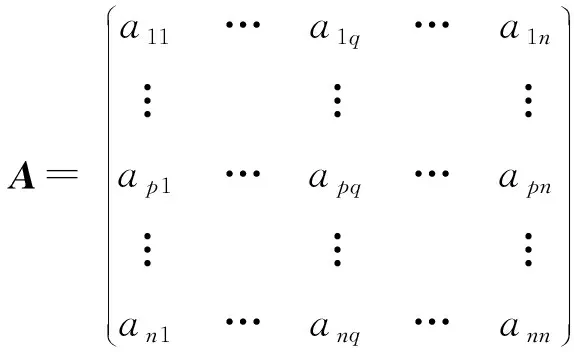
(2)

其中，apq为类簇Cp至类簇Cq的乘客出行量。

将各类簇的质心设置为类簇内样本点的坐标平均值，并建立各类簇间的出行距离矩阵B：

(3)

其中，bpq为类簇Cp至类簇Cq质心之间的距离。考虑类簇间客流强度和出行距离对类簇重要度的影响，类簇间客流量越大，出行距离越短，则该类簇重要度越高，得出类簇重要度的计算公式如下：

(4)

对上述两个指标进行量纲的统一，得出精细化服务指标为：

χ=αSSECp+ωβCIMPCp，

(5)

其中，ω为量纲统一系数，因类簇重要度为整数，而类簇内离散程度为小数，该系数设置不影响结果，得出的量纲统一系数是为了方便计算。

2.1.2 聚类参数Eps和minPts的选择

根据2.1.1可知，对于精细化服务指数较高的类簇，需要利用DBSCAN算法对其进行进一步聚类，而初始聚类的参数Eps和minPts已经不适用精细化聚类的要求[19]。在定制商务班车发展尚不成熟的条件下，根据经验改变聚类参数可能会出现较大误差。同时统一改变聚类参数，将其作为精细化聚类的全局变量无法体现定制商务班车因地制宜的特点。因此，本文提出利用最大最小值距离法(maximum and minimum distance, MMD)[20]，根据数据特征自适应更新聚类参数，得到最适用于该类簇更新的聚类参数。

聚类参数Eps和minPts的更新方式为：针对待精细化的类簇Cu,分别计算其任意两个样本间的距离，得到样本距离集合ECu：

ECu=(e1,e2,…,em,…)

。

(6)

统计集合中ECu中最小最大距离值min(ECu),max(ECu)，将其差值max(ECu)-min(ECu)划分为z个不同的取值区间，考察每一区间包含的样本对数，并构建统计量HCu:

(7)

其中，lz为第z个区间内包含的样本对数。找到包含最多样本对数的区间号h，则类簇Cu对应的更新后的Eps的参数值为第h个区间对应样本距离的中心值，该中心值的计算方法为：

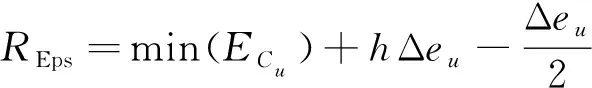
(8)

其中，Δeu=[max(ECu)-min(ECu)]/z。更新后的minPts的值则为类簇Cu中所有样本在更新后的ε邻域内包含的样本量的最大值。

2.1.2 聚类中心计算与站点选址

聚类得到的各类簇经过精细化衡量之后，通过自适应调整聚类参数进行进一步聚类，最终使得全部类簇不需要再进行精细化，此时得到的类簇即为可进行选址依据的类簇。而基本的DBSCAN算法不能生成聚类中心，传统的聚类算法对于聚类中心的计算主要以欧氏距离最小为依据[21]。

传统的公交站点选址方法主要是根据交通部门划分的线路，在城市道路实地考察，偏重问卷调查和实地访问，最后汇总市民意见，根据需求呼声最大的确定线路建设方案[22]。定制商务班车根据乘客个性化需求，通过集合这些需求的共同点，以多人共用交通工具的形式设定线路，是为出行起讫点、出行时间、服务水平需求相似的人群提供量身定制的客运服务方式，具有定点、定时、定车、定人等特点和“一人一座、一站直达、线路灵活”等优势。在国内，定制商务班车具有服务范围大、乘客规模相对较小、线路设计灵活、需求响应迅速、按需而设、乘客黏度较高等特点。因此，在定制商务班车的站点选址过程中，要尽可能地选择有利于大站开行，道路条件优良，有利于发挥定制商务班车速度快、质量高的地点，因而在选址过程中应该考虑公交专用道、公交快线的远近。同时由于轨道交通站点附近客流疏散能力较强，可以作为定制公交站点选址的参考。

所以，本文引入节点重要度的思想，将不需精确化的类簇中的样本点作为备选节点，建立网络拓扑结构指标，对各节点的重要度进行评价作为选址的依据。

类簇Cv内样本点j的网络拓扑结构指标值为：

δWTj=ρ×fjr+ρ×fjb+γ×fjz,

(9)

式中，fjr为样本点j连接轨道线路的边数；fjb为样本点j连接BRT公交快线的边数；fjz为样本点j连接的城市道路可用于公交专用道的车道数；ρ、φ、γ分别为fjr,fjb,fjz的权重系数，可通过专家咨询法和层次分析法来确定，本文建议ρ=1,φ=0.8,γ=0.5。

类簇Cv内样本点j的节点重要度为：

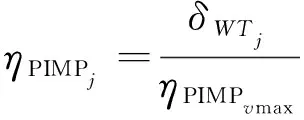
(10)

式中，ηPIMPvmax为类簇Cv内所有样本点重要度的最大值。类簇内各节点的重要度为接下来的选址提供了依据，对各样本点的重要度进行评级，重要度越低的样本点赋予较大的惩罚系数，使其在聚类过程中有较大的距离，不易被选中，惩罚系数指标如表1所示。

表1 距离惩罚系数指标

计算类簇内各样本点间的距离集合，得到任一样本点到其他样本点的距离中位数并通过距离惩罚系数换算成选址距离，比较各样本点的选址距离，选址距离最短的即为选址点。

2.2 改进的DBSCAN算法流程

改进的DBSCAN算法流程如图2所示。

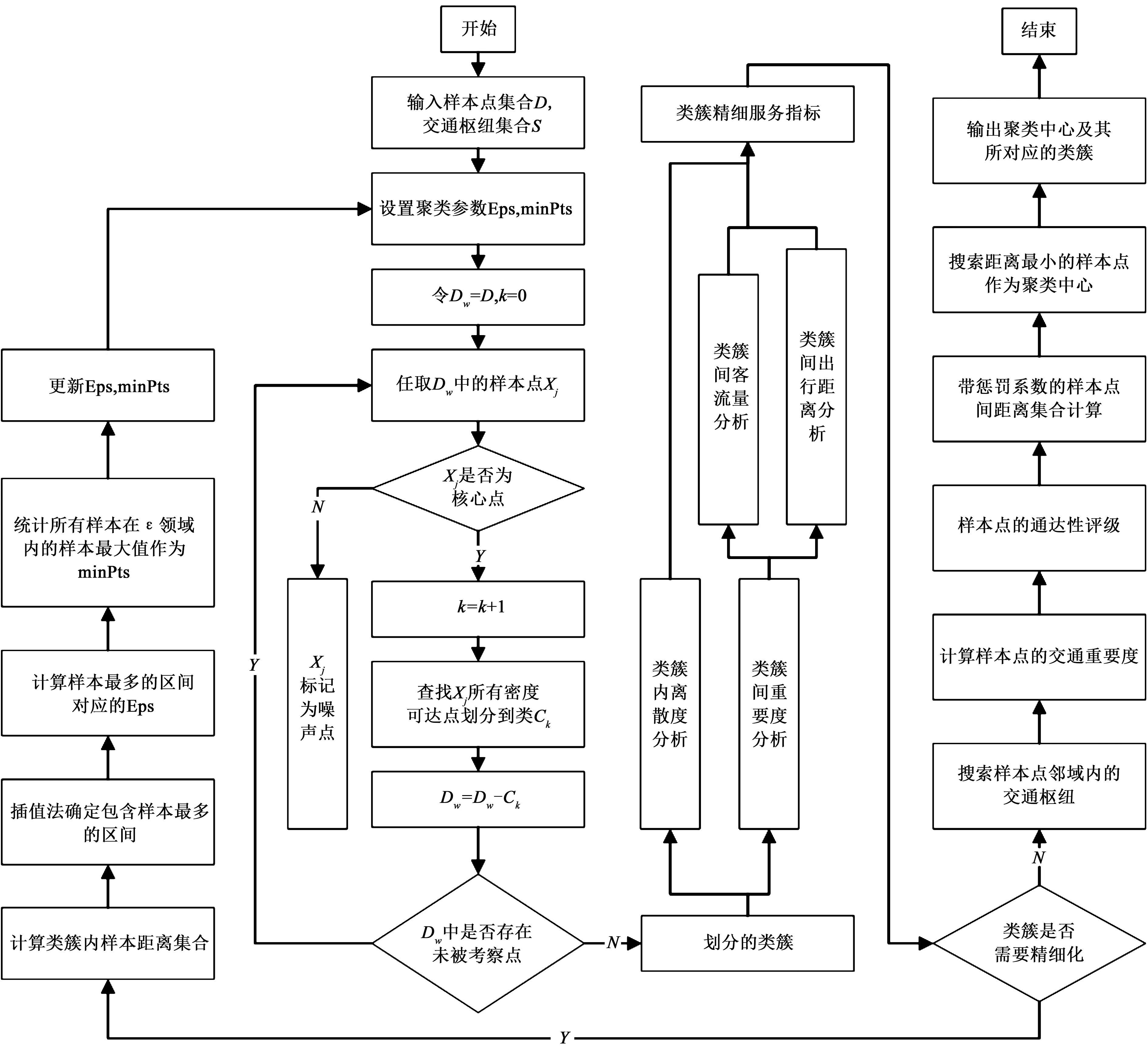
图2 改进的DBSCAN算法流程Fig. 2 Improved DBSCAN algorithm flow

输入：乘客出行需求调查样本点集合D，公交站、地铁站等交通枢纽分布集合S。

输出：基于乘客需求数据的定制商务班车站点建议选址坐标。

步骤1：初始化未访问样本点集合Dw=D,类簇序号k=0，待精细化簇集合Djx=∅，类簇划分集合Crc=∅。

步骤2：根据类簇序号k设置并更新其对应的聚类参数Eps和minPts，k=0时，依据站点布设经验设置初始参数Eps=10, minPts=1000。

步骤3：任意选择Dw中的一个点xj。若xj为非核心点，则执行步骤4；若xj为核心点，则执行步骤5。

步骤4：将xj标记为噪声点，并从集合Dw中删除。

步骤5：令k=k+1，确定D中所有与xj密度可达的点，并把xj及其密度可达点划分到类Ck中，并将Ck中的点从集合Dw中删除。

步骤6：若Dw=∅，则输出类簇划分的结果Crc={C1,C2,…,Ck}, 否则转到步骤3。

步骤7：对于划分得到的任意类簇Cq∈Crc，依据2.1.1节计算其精细化服务指标。

步骤8：若该类簇的精细化服务指标达标，则将其归入Cjx，更新簇Crc=Crc-Cjx。

步骤9：若Cjx=∅，则转入步骤11,否则对Cjx内任意类簇Cu根据2.1.2的方法计算并更新其对应的Eps和minPts，转入步骤2。

步骤11：对Crc内的各类簇Cv，根据2.1.3的理论计算并输出其建议选址位置。

3 案例分析

3.1 出行需求数据分析与处理

本文通过北京市定制商务班车电子商务平台，采集到了从2016年1月到2016年7月共计1 701条定制商务班车乘客出行需求数据。鉴于站点选址要在乘客出行点位置分布的基础上进行自适应聚类，因此，从基础数据中提取乘客出行需求中的出发地和到达地两项数据，通过筛选整理得到如表2所示的定制商务班车乘客出行地址统计表。

表2 定制商务班车乘客需求点统计表

由表2可见，采集到的乘客信息主要是地址的描述，在进行分析时需要将其转变为地理坐标数据。因此，需要利用大批量地址经纬度解析转换工具XGeocoding进行解析，得到每个出行需求的经纬度坐标。基于得到的坐标，将乘客的出行需求点绘制成分布图如图3所示。

图3中底图为北京市路网分布图，从图中可以直观地看到乘客出行需求在市区的分布情况：大部分的乘客需求位于六环以内，且越靠近城区需求点越密集。由于北京市的路网呈环形放射状，一些从市中心延伸出来的主干路的沿线也有较多的需求分布，这些需求随着路网的走向在空间呈条形分布，离散程度较大，不利于聚类的进行。还有一小部分需求点位于京郊区县，这些需求点与主城区的节点群间隔很大，进行聚类时也应注意排除这些节点的影响。

3.2 聚类分析与精细化衡量

在对需求数据的空间特征进行简单的分析后，结合站点规划理论[23]和定制商务班车的服务经验[24]，确定定制商务班车粗略选址的条件为满足周边半径1 000 m区域大于10人次的出行需求。故设置初始聚类参数Eps=1 000，minPts=10，运行DBSCAN算法进行初始聚类，得到的类簇分布如图4所示。

图3 北京市需求点分布Fig. 3 Distribution ofdemand point in Beijing

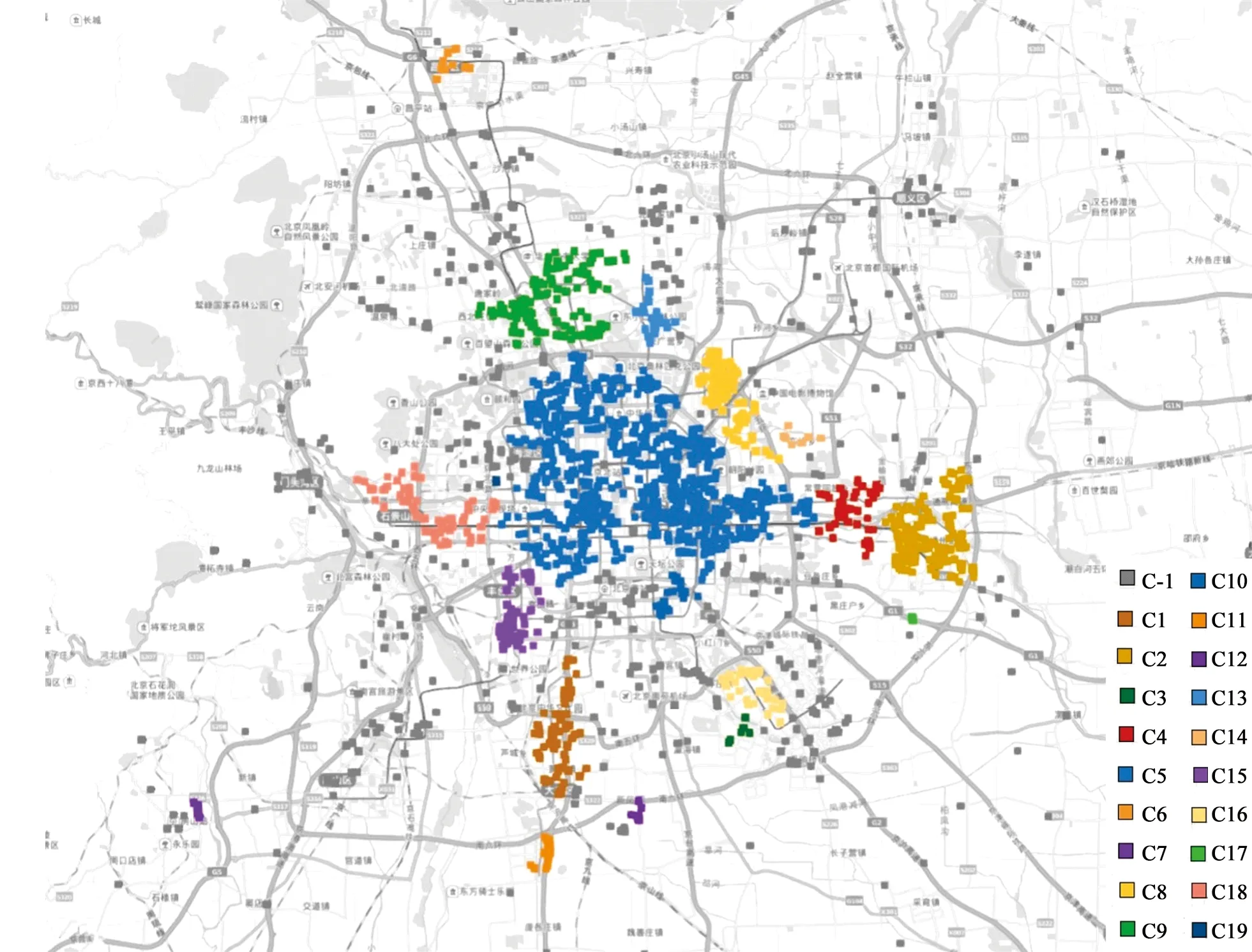
图4 带噪声点的分类结果Fig.4 Classification results with noise points

由图4可见，DBSCAN算法自动识别并排除了噪声点的影响，将剩下的需求点依据数据特征自动划分为19个类簇组。通过对比图3和图4，我们可以看到大部分分布于京郊区县且离散程度很大的节点都被识别成为噪声点，剩下来的节点大多位于中心城区且分布较为稠密，这证明DBSCAN算法能有效规避数据离散程度过大点的影响，并且能够较合理地进行类簇划分，是需求点聚类的理想选择。但同时也可以看出，以图中类簇C5为代表的一些类簇组位于三四环核心区域，乘客需求多且分布广，以图中类簇C1为代表的一些类簇组分布狭长，乘客步行时间长。在这两类地区，定制商务班车有必要进一步增设站点，提供精细化服务。

为了识别出需要增设站点的类簇，依据2.1.1论述的方法计算各类簇的精细化服务指数，结果如表3所示。

表3 各类簇精细化程度指标

根据定制商务班车服务理论[25]，本文取精细化服务判别的阈值为0.5。由表3中可看出，需要进一步增设站点的类簇组号为C1、C3、C5、C8、C9、C15、C16，这与图4中分布在城市中心圈或者分布狭长的类簇相吻合。在这些类簇中，由于类簇C3的需求点过少，为节约建设资源，暂不考虑对其进行精细化聚类。由此得出，最终待精细化聚类的类簇组号为C1、C5、C8、C9、C15、C16。

根据前述理论可知，待精细化的类簇需要DBSCAN算法根据其自身数据特点更新聚类参数Eps和minpts,根据2.1.2节的思想，计算各区间的Eps和minPts，得到的结果如表4所示。

表4 更新的各类簇聚类参数值

利用得到的聚类参数重新控制DBSCAN算法进行聚类，并将得到的结果进行精细化衡量，直到所有类簇不再需要精细化为止。

3.3 类簇聚类中心确定与对比

得到的类簇需要结合节点重要度和区位重要度计算聚类中心，在第一次聚类得到的类簇组C1，经二次聚类后得到了6个组，经过精确化指标检验，不需再进行进一步聚类，下面选取C1组精细化聚类得到的最终类簇中的第4组(即为C1-4组)为例计算聚类中心，组内各需求点分布如图5所示。

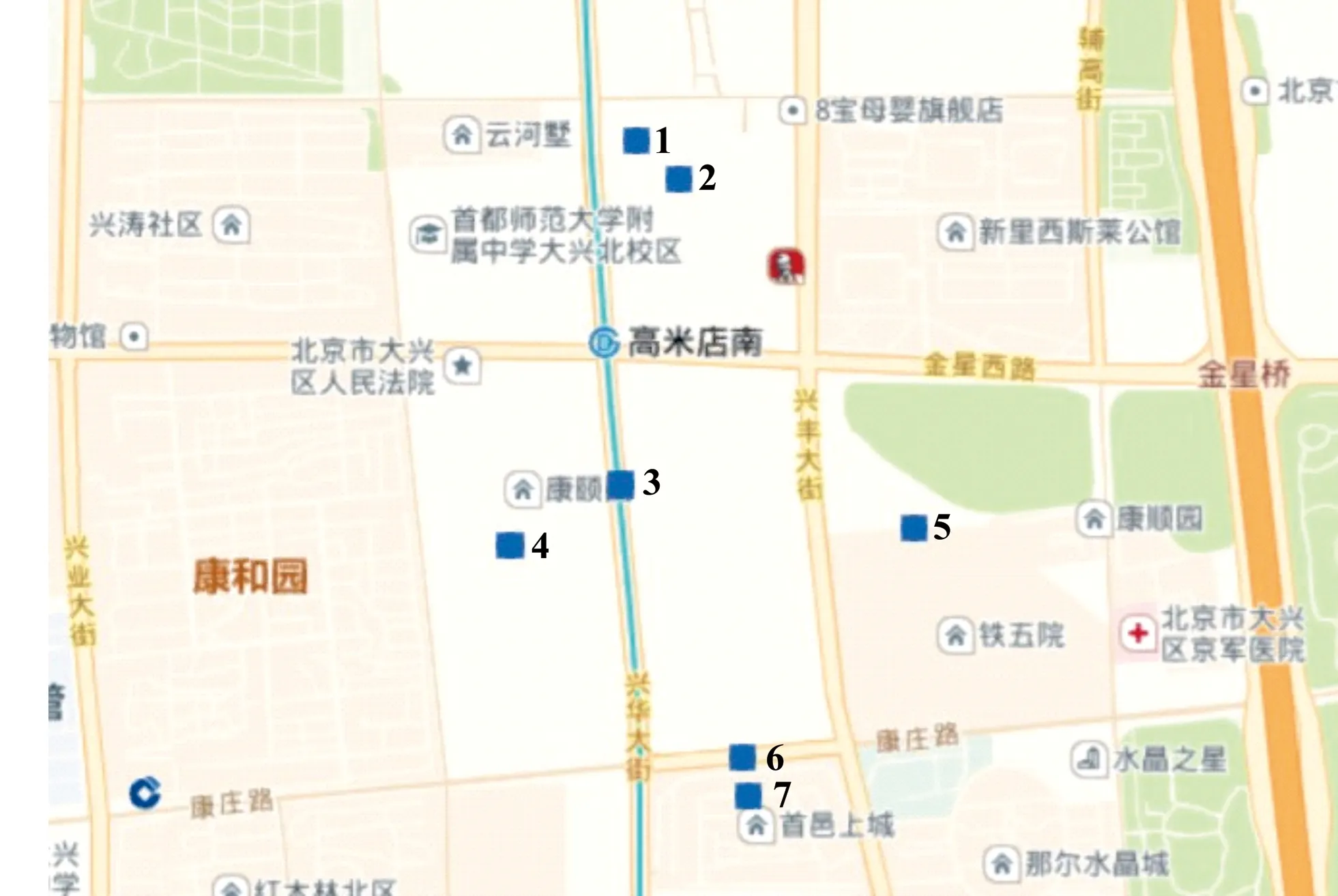
图5 C1-4组聚类节点分布情况Fig.5 Distribution of cluster nodes in C1-4 Group

根据各需求点周围的交通枢纽分布情况，结合2.1.3的思想计算类簇内各样本点的节点重要度，并据此得出节点层级及其对应的惩罚系数，对样本点间的实际距离结合惩罚系数换算，各样本点的距离中位数如表5所示。

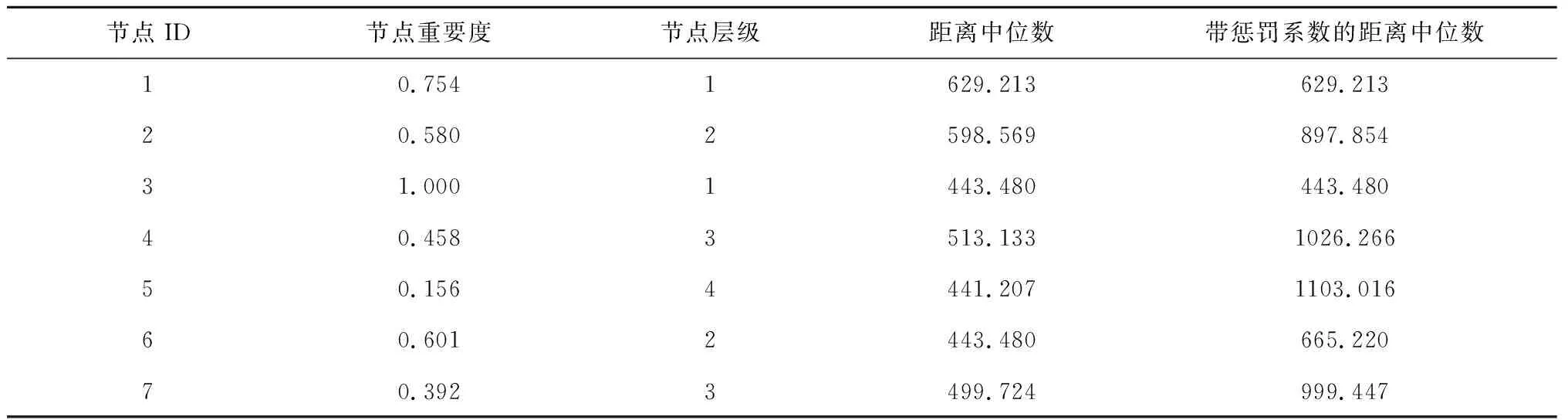
表5 组内各样本点距离中位数

由表5可知，样本点3与其他样本点间的距离经惩罚系数换算之后最小，因而可以确定样本点3为类簇C1-4的聚类中心。根据以上结果，得出待精确化组的最终的聚类各点坐标如表6所示。

表6 改进的DBSCAN最终聚类结果

聚类中心分布如图6所示，由图中可看到，考虑节点重要度的各类簇的聚类中心点都分布在主要交通干路上。

利用K-means算法聚类，将得到的中心与改进的DBSCAN算法得到的聚类中心进行对比，结果如图7所示。图7中较大的点代表利用K-means算法得到的聚类中心，较小的点代表利用改进的DBSCAN算法得到的聚类中心。由图中可见，改进的DBSCAN算法能够有效地规避噪声点的影响，所选取的聚类中心更趋向于需求点稠密的中心区域，该算法能够依据类簇的数据分布和区位特征调整聚类中心的个数，需求点多且分散的集群分配了较多的备选站点，同时这些备选站点自身也分布于交通通达性较高的地点，能够充分利用周围的交通资源，便于缩短乘客的换乘时间和步行距离，有利于公交网络的构建。

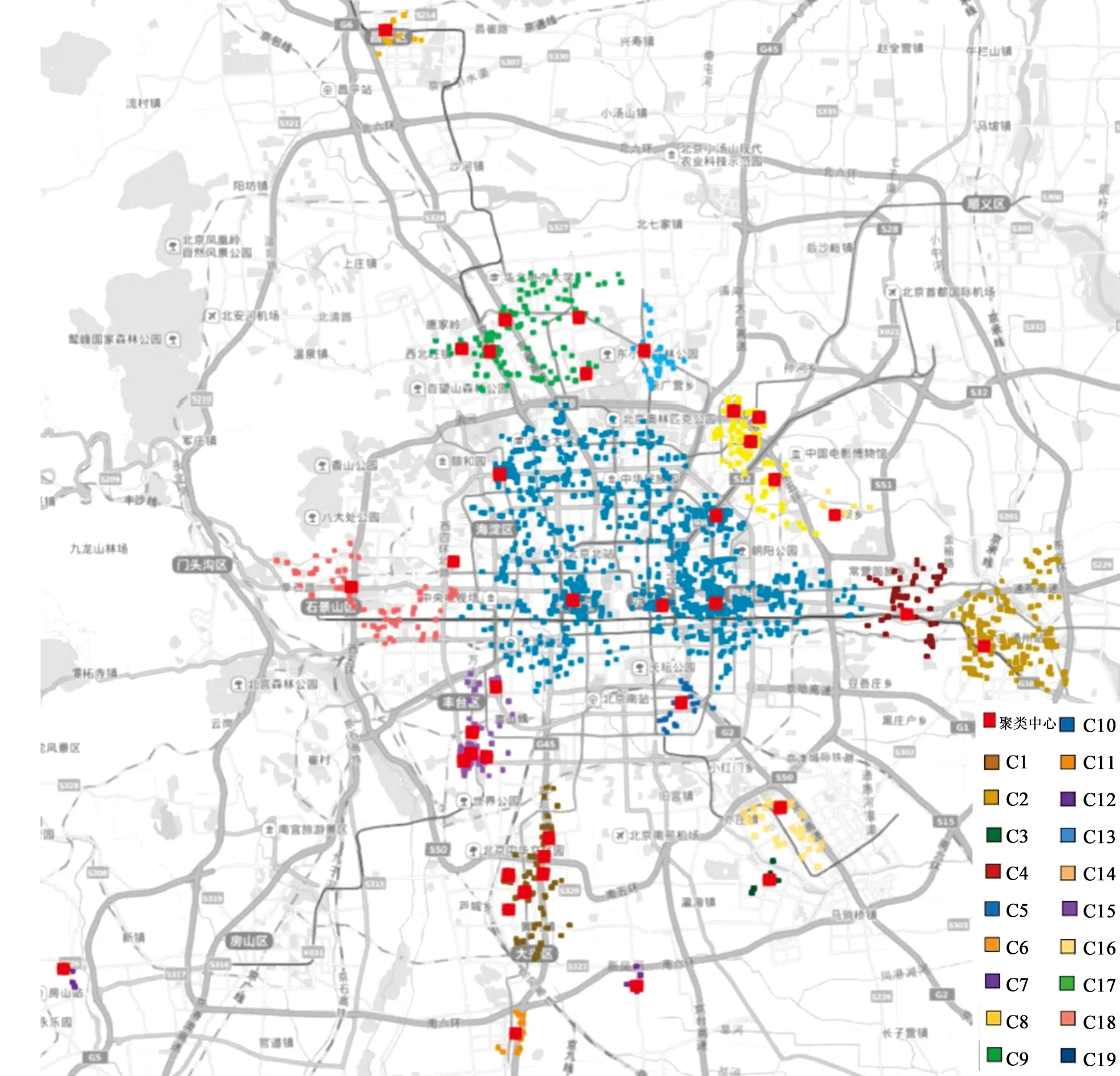
图6 改进的DBSCAN聚类中心分布情况Fig.6 Improved DBSCAN cluster center distribution

图7 两种算法所得的聚类中心对比Fig.7 Comparison of cluster centersfrom two algorithms

4 结语

本文对DBSCAN算法的优缺点进行了研究，分析了聚类参数质量对聚类结果的影响，提出了DBSCAN算法动态选择方法，同时结合区位重要度分析，考虑各类簇至其他类簇的空间距离和类簇间的客流强度，确定相关类簇是否需要进一步精细化，其布局结论可以保证类簇和其他分区之间具有较好的可达性以及实现类簇客流来源的极大化。在聚类中心的确定中，考虑到城市建成区难以满足公交枢纽建设用地要求，所以在有限满足类簇内需求点的出行，根据区域节点重要度确定枢纽布局方案，提高了站点选址的实用性。本文提出的算法减轻了对聚类参数的依赖，同时改进了聚类中心的选择。在对基本的DBSCAN算法进行改进、增加其功能的同时，可能使得算法计算聚类中心的时间较长，下一步的研究可以对算法进行进一步优化，争取在实现功能的同时减少算法运算时间，使其能更快地完成站点选址的目标。