多元化解题方法在高中数学函数题型中的应用

刘天乐

摘要：我们所学的高中数学的函数是初中函数的延伸，其变量关系更加复杂。思路清晰是数学解题的一个重要因素，有了正确的解题思路，题目就已经解决一半了，达到事半功倍的效果。同样解题思路应该具有灵活性，如果限制在一定框架内，人的思维就会变得僵化，无法快速地分析题目，找出解答的办法。所以在解答题目时要开放思维，才能让解题方式变得多元化。基于此，笔者对高中函数作了一个简要的概述，并在此基础上从四个常见的主要方法来探析多元化解题方法在高中函数题型中的应用，仅供参考。

关键词：高中数学 函数 解题方法 应用

一、引言

数学是我们学习过程中最重视的学科之一，不仅是因为它的实用性强，更是因为数学本身的灵活与难度。其中，函数是高中数学最重要的内容之一，学习难度也相当大，将多元化的解题方法应用到函数题目中不仅能减轻学习函数的难度，有助于提高学习热情和效率。多元化的解题方法，在增强同学们学习的创新型、自主性方面有着重要的作用。对于一般的函数题目用一般方法即可解决，但是在面对拔高型函数题目时，多元化、灵活的解题方法就显得尤为重要。本文以高中数学函数习题为例，对多元化的解题方法进行了详细的研究与分析，达到提升同学们学习效率的作用。

二、多元化解题方法在高中数学函数题型中的应用

（一）数形结合法

每一道题目的图像里都蕴藏着一定的数量关系，图像能将数量关系直观地表现出来，所以在解决数学问题时，常常将数的问题转化成直观的图形来观察，赋予几何意义，同样性的条件也可以转化为数去思考，分析其中的代数意义。如此将数与形巧妙融合去解决数学问题，就是数形结合法。而函数则是集图像和几何于一身，表达式由几何表示，同时又具有图像这一特征，两者紧密结合，所以数形结合法被十分普遍地运用到函数问题中。例如在解决三角函数问题时，一般利用数形结合法来解决与三角函数单调区间或三角函数值大小等问题。

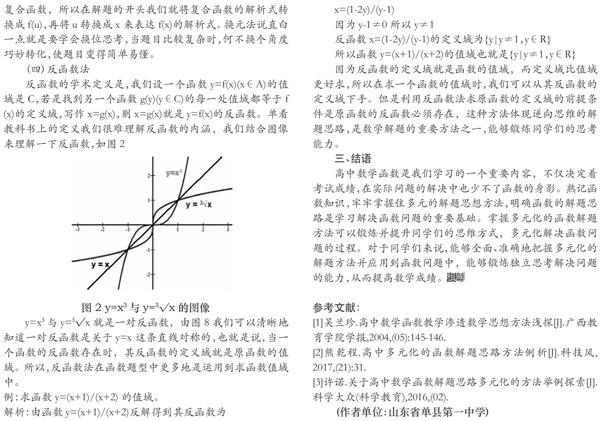
因为反函数的定义域就是函數的值域，而定义域比值域更好求，所以在求一个函数的值域时，我们可以从其反函数的定义域下手。但是利用反函数法求原函数的定义域的前提条件是原函数的反函数必须存在，这种方法体现逆向思维的解题思路，是数学解题的重要方法之一，能够锻炼同学们的思考能力。

三、结语

高中数学函数是我们学习的一个重要内容，不仅决定着考试成绩，在实际问题的解决中也少不了函数的身影。熟记函数知识，牢牢掌握住多元的解题思想方法，明确函数的解题思路是学习解决函数问题的重要基础。掌握多元化的函数解题方法可以锻炼并提升同学们的思维方式，多元化解决函数问题的过程。对于同学们来说，能够全面、准确地把握多元化的解题方法并应用到函数问题中，能够锻炼独立思考解决问题的能力，从而提高数学成绩。

参考文献：

[1]吴兰珍.高中数学函数教学渗透数学思想方法浅探[J].广西教育学院学报，2004，（05）：145-146.

[2]熊乾程.高中多元化的函数解题思路方法例析[J].科技风，2017，（21）：31.

[3]许诺.关于高中数学函数解题思路多元化的方法举例探索[J].科学大众（科学教育），2016，（02）.

（作者单位：山东省单县第一中学）