深埋地下人员密集场所电梯与楼梯协同疏散的电梯运行参数研究
2019-02-22李田生邓建国秦焰宏牟玉斌秦学思
李田生,邓建国,秦焰宏,骆 骊,牟玉斌,秦学思
(1.重庆城市综合交通枢纽开发投资有限公司,重庆 400015; 2.西南交通大学地球科学与环境工程学院,四川 成都 611756)
随着经济社会的高速发展,城市核心区域各类深埋地下人员密集场所不断涌现,如我国各大城市的地下城市综合交通枢纽、地铁换乘站和地下商场等。例如以重庆市沙坪坝综合交通枢纽(以下简称“沙坪坝枢纽”)为例,其地下共有7层,地下埋深为36.5 m,高峰时段人员达14 238人,若不考虑人员上行疏散过程中疲劳度的影响,人员整体疏散时间超过0.6 h,若考虑人员疏散疲劳度的影响,人员整体疏散时间将超过1.2 h。深埋地下空间的特性使得火灾条件下排烟排热效果差、火灾扑救难度大,故而传统的楼梯疏散已经难以满足人员整体安全疏散的需求,因此探索地下深埋人员密集场所电梯与楼梯协同疏散的可行性以及协同疏散的策略已成为国际上人员安全疏散领域的又一大热点问题。
目前国外学者针对电梯疏散的研究工作取得了一些成果。在国外,20世纪中叶,一些学者就开始了超高层建筑利用电梯疏散问题的研究工作[1];1974年,Bazjanac[2-3]提出了火灾时考虑另一个安全出口疏散的思路,同时对紧急情况下电梯疏散的性能进行了分析;20世纪80年代,Klote[4-6]研究了电梯辅助老弱病残等群体疏散的可行性,并总结出标准公式克服疏散时可能出现的活塞效应;20世纪90年代,Klote等[7-8]在研究利用电梯进行人员疏散可行性的基础上,提出了电梯紧急疏散系统(EEES)的概念;20世纪90年代,ASME、NFPA、NIST举行了一系列电梯疏散的学术会议[9],在美国“9·11”事件之后,NIST于2008举行了“Rethinking Egress”会议,探讨了电梯疏散的优点;2015年,Shin[10]提出了用作自动喷水灭火系统和智能手机辅助疏散系统的电梯系统的撤离指导;2016年,Andree等[11]通过虚拟现实(VR)实验,研究了出口选择和高层建筑电梯疏散的等待时间。
在国内,许多学者围绕电梯疏散的可行性也开展了大量研究。如胡传平等[12]和宋文华等[13]针对高层建筑疏散的困境,采用数值模拟方法对比研究了采用楼梯和电梯进行疏散的有效性,并搜集现有成功采用电梯疏散的案例,进而阐明了楼梯与电梯协同疏散的可行性;陈辉等[14]针对高层建筑火灾安全学的发展提出了“安全核”疏散体系的概念;张虎南[15]研究指出超高层建筑避难层应设置安全疏散电梯;胡传平等[12]利用电梯疏散ELVAC模型,研究了电梯数量、人员分布等对电梯疏散的影响;朱惠军[16]分析了采用高速穿梭电梯作为辅助疏散的新型疏散体系的可行性;李钊等[17]研究了Evacnet模型下的电梯疏散时间和电梯疏散效率的变化规律。
综上可见,国内外学者围绕电梯疏散进行了大量的研究,但是针对深埋地下人员密集场所电梯与楼梯协同疏散的研究还较缺乏。因此,为了探索城市核心区深埋地下人员密集场所电梯与楼梯协同疏散的可行性和最优的电梯运行参数,本文以重庆沙坪坝地下综合交通枢纽为研究对象,利用Pathfinder疏散软件建立了沙坪坝地下综合交通枢纽人员疏散模型,研究了134种疏散场景下电梯运行参数对疏散时间的影响规律,并在此基础上给出了该地下综合交通枢纽电梯与楼梯协同疏散过程中电梯运行参数的最优建议取值,以为深埋地下人员密集场所电梯与楼梯协同疏散设计提供技术支撑。
1 疏散场景及模型参数设置
1. 1 疏散场景设置
重庆沙坪坝地下综合交通枢纽工程总建筑面积约 75万m2,其中地上约 51万m2,地下约 24万m2;地下7层布置有商业、公交车站、出租车站、换乘系统和地下停车场,地上布置了5栋超高层办公写字楼、1栋高层酒店、1栋高层办公写字楼。为了探索该深埋地下人员密集场所楼梯与电梯协同疏散过程中电梯运行参数对疏散时间的影响,考虑到模型中最不利情况下约有14 238人,为了方便模拟,忽略了负四层及以上楼层人员采用电梯疏散的方案,只考虑了3种人员疏散方案,方案一、方案二和方案三分别为:负七层的人员采用电梯疏散,负六层至负一层的人员采用楼梯疏散;负七层和负六层的人员采用电梯疏散,负五层至负一层的人员采用楼梯疏散;负七层至负五层的人员采用电梯疏散,负四层到负一层的人员采用楼梯疏散。取电梯运行参数为Pathfinder软件默认值,模拟得到3种人员疏散方案下的疏散时间分别为2 293.4 s、2 098.3 s和2 892.6 s。由此可见,所选方案中采用方案二进行人员疏散时所用的疏散时间最少,故以该方案来模拟电梯与楼梯协同疏散可相对节省模拟所用的时间。在此基础上,本次模拟设置的疏散场景如下:
(1) 疏散场景A:电梯加速度改变,不变的电梯运行参数为:电梯荷载取13人,电梯额定最大速度取5 m/s,电梯开关门时间取7 s,共有11种疏散场景,见表1。

表1 疏散场景A:电梯加速度改变,其他电梯运行参数恒定
(2) 疏散场景B:电梯开关门时间改变,不变的电梯运行参数为:电梯荷载取13人,电梯额定最大速度取5 m/s,电梯加速度取1.2 m/s2,共有8种疏散场景,见表2。

表2 疏散场景B:电梯开关门时间改变,其他电梯运行参数恒定
(3) 疏散场景C:电梯荷载和电梯额定最大速度改变,不变的电梯运行参数为:电梯开关门时间取7 s,电梯加速度取1.2 m/s2,共有35种疏散场景,见表3。

表3 疏散场景C:电梯荷载和电梯额定最大速度改变,其他电梯运行参数恒定
(4) 疏散场景D:电梯荷载和电梯加速度改变,不变的电梯运行参数为:电梯开关门时间取7 s,电梯额定最大速度取5 m/s,共有35种疏散场景,见表4。

表4 疏散场景D:电梯荷载和电梯加速度改变,其他电梯运行参数恒定
(5) 疏散场景E:电梯额定最大速度和电梯加速度改变,不变的电梯运行参数为:电梯开关门时间取7 s,电梯荷载取12人,共有25种疏散场景,见表5。
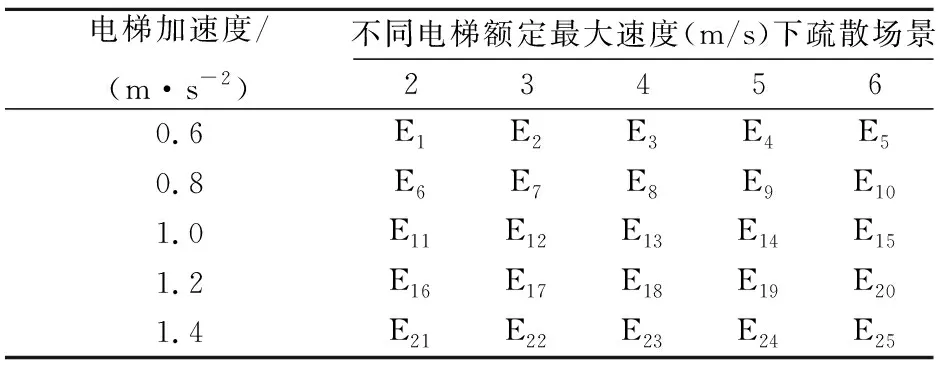
表5 疏散场景E:电梯额定最大速度和电梯加速度改变,其他电梯运行参数恒定
(6) 疏散场景F:电梯额定最大速度改变,不变的电梯运行参数为:电梯荷载取13人,电梯开关门时间取7 s,电梯加速度取1.2 m/s2,共有11种疏散场景,见表6。
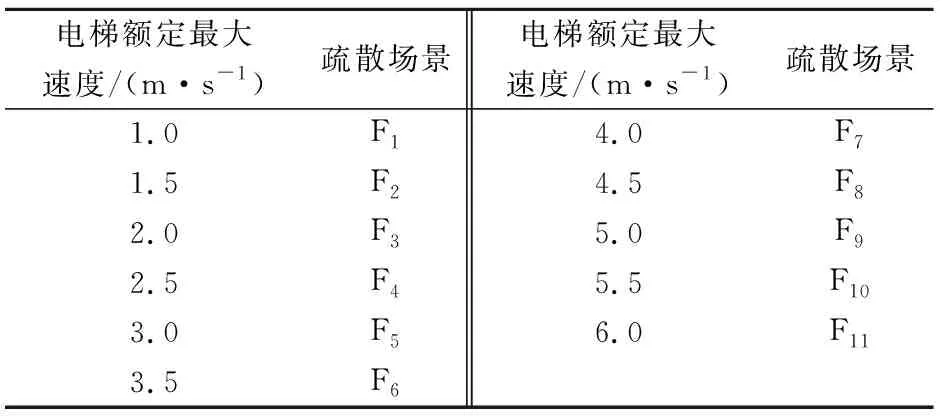
表6 疏散场景F:电梯额定最大速度改变,其他电梯运行参数恒定
(7) 疏散场景G:电梯荷载改变,不变的电梯运行参数为:电梯额定最大速度取5 m/s,电梯开关门时间取7 s,电梯加速度取1.2 m/s2,共有9种疏散场景,见表7。

表7 疏散场景G:电梯荷载改变,其他电梯运行参数恒定
1. 2 人员参数设置
《重庆沙坪坝铁路枢纽综合改造工程性能化防火设计》报告中对高峰人流量进行了计算,计算公式为:人员数量=高峰每小时人数×超高峰系数×停留时间(min)÷60。根据该报告中的计算结果,在最不利情况下沙坪坝地下综合交通枢纽的人数为14 238人,根据前述的负七层和负六层的人员采用电梯疏散,其余楼层的人员采用楼梯疏散的疏散方案(即方案二),高峰时负七层和负六层各有3 659人和1 848人,故电梯承担疏散人员的总负荷为5 507人。该建筑各场所具体疏散的人员数量见表8。

表8 建筑各场所疏散的人员数量(人)
沙坪坝地下综合交通枢纽内的人员可分为成年男士、成年女士、儿童和老人4种类型,根据其使用功能,其人员类型组成可参照国际上通用的一般公共建筑场所推荐的数值比例设置。其中,站房候车区、站台层以及出站区内人员类型的构成为:成年男士和成年女士各占40%,老人和儿童各占10%;各功能房间内人员类型的构成为:成年男士占60%,成年女士占40%。
根据Chen等[18]关于人员长距离上行疏散研究得出的结论:在拥挤条件下,人员在每个楼层的平均上行速度保持约为0.5±0.04 m/s的相对恒定值。因此,考虑疲劳度的条件下模型中所有人员的初始上行疏散速度均取0.5 m/s。
1. 3 电梯参数设置
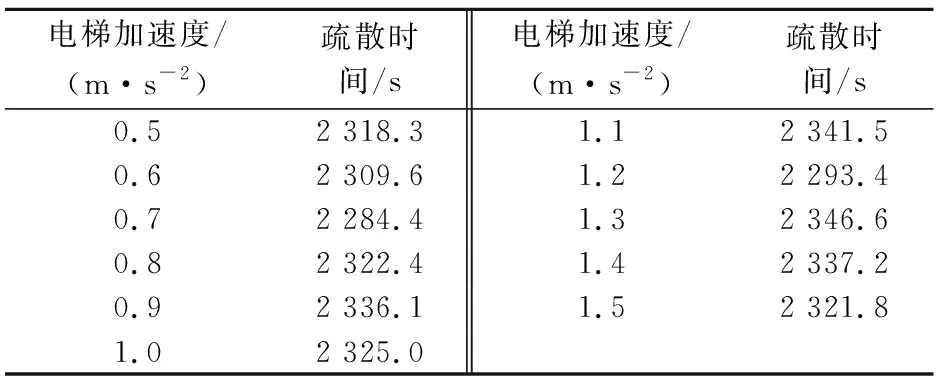
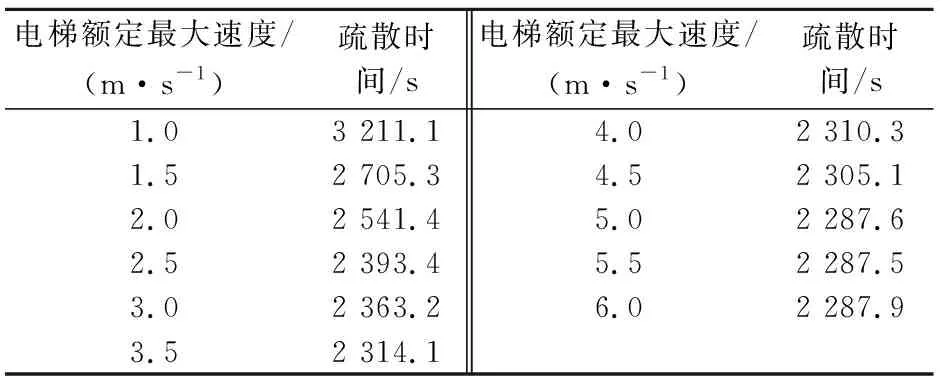
电梯运行参数的设定本文根据《电梯技术条件》(GB/T 10058—2009)[19]标准中的规定:当电梯额定最大速度为0 m/s 为了得出电梯运行参数对疏散时间的影响程度,本文采用控制变量法,分别模拟得到不同疏散场景A、B、F和G下电梯加速度、电梯开关门时间、电梯额定最大速度和电梯荷载与疏散时间的关系,详见表9至表12。 表9 电梯加速度与疏散时间的关系 表10 电梯开关门时间与疏散时间的关系 表11 电梯额定最大速度与疏散时间的关系 表12 电梯荷载与疏散时间的关系 根据表9至表12,利用SPSS软件分别对这4个电梯运行参数与疏散时间进行了相关性分析,得到显著性水平为0.01时的相关系数分别为0.001、0.997、-0.889和-0.775。由此可见,电梯荷载、电梯额定最大速度和电梯开关门时间与疏散时间的相关性较大,而电梯加速度与疏散时间的相关性很小,这可能是由于对于深埋地下仅有7层的沙坪坝地下综合交通枢纽,不同电梯加速度下电梯疏散到地面所用的时间相差不大所致。因此,电梯运行参数对疏散时间的影响程度从大到小的排序为:电梯开关门时间>电梯额定最大速度>电梯荷载>电梯加速度。 根据疏散场景B,本文模拟得到的电梯开关门时间与疏散时间的关系曲线,见图1。 图1 电梯开关门时间与疏散时间的关系曲线Fig.1 Relationship curve between door opening-and-closing time of elevator and evacuation time 由图1可见,电梯开关门时间与疏散时间基本成正比关系,说明电梯的开关门时间越短,越有利于人员疏散。尽管电梯开关门时间越短电梯总的人员疏散时间也越少,但如果电梯开关门时间太短,候梯人员在进入电梯时可能会造成夹伤等事故,也会严重阻碍电梯的疏散效率,增加额外的电梯疏散时间。因此,电梯开关门时间要在保证人员能够安全进出电梯的情况下尽可能地取最大值。根据《电梯技术条件》(GB/T 10058—2009)[19]标准中的规定,对于门的形式为中分自动门的电梯,开门宽度不大于800 mm时,电梯开关门时间应不大于3.2 s,结合沙坪坝地下综合交通枢纽的实际情况,建议最优电梯开关门时间取为3 s。 在疏散场景C、D、E下,本次模拟得到的电梯运行参数与疏散时间的关系曲线,见图2、图3和图4。 图2 不同电梯荷载下电梯额定最大速度与疏散时间的关系曲线Fig.2 Relationship curve between elevator speeds and evacuation time under different elevator loads 图3 不同电梯加速度下电梯额定最大速度与疏散时间的关系曲线Fig.3 Relationship curve between elevator speed and evac-uation time under different elevator accelerations 图4 不同电梯加速度下电梯荷载与疏散时间的关系曲线Fig.4 Relationship curve between elevator load and evacuation time under different elevator accelerations 由图2可见,在电梯荷载一定时,疏散时间随着电梯额定最大速度的变化曲线先下降,直至电梯额定最大速度达到约5 m/s后,疏散时间趋于一个稳定值不再变化;当电梯荷载增加时,疏散时间随着电梯额定最大速度的变化曲线分布较为稀疏,当电梯荷载达到约14人时,电梯荷载的变化对电梯额定最大速度与疏散时间关系的影响不大,该曲线整体的变化趋势是电梯荷载越大,电梯额定最大速度越大,疏散时间会越短。 由图3可见,当电梯加速度一定时,疏散时间随着电梯额定最大速度的变化曲线先下降,直至电梯额定最大速度达到约5 m/s后,疏散时间趋于一个稳定值不再变化;当电梯额定最大速度在1~5 m/s之间时,不同电梯加速度下的疏散时间最多相差300 s;当电梯额定最大速度达到约5 m/s后,不同电梯加速度下疏散时间基本相同,疏散时间随着电梯额定最大速度的变化曲线分布较为密集,该曲线整体的变化趋势是电梯加速度越大,电梯额定最大速度也越大,疏散时间会越短。 由图4可见,在电梯加速度改变时,疏散时间随着电梯荷载的变化曲线先下降,直至电梯荷载达到约14人后,疏散时间趋于一个稳定值不再变化;在误差允许的范围内,不同电梯加速度下疏散时间随着电梯荷载的变化曲线分布基本重合,这说明电梯加速度增大时,疏散时间随着电梯荷载变化的规律是不变的,且疏散时间的大小只与电梯荷载有关。 对比图2、图3和图4可见,电梯荷载和电梯额定最大速度对疏散时间的协同影响最大,电梯加速度和电梯额定最大速度对疏散时间的协同影响较小,电梯加速度和电梯荷载对疏散时间的协同影响最小。 综上分析可见,对沙坪坝地下综合交通枢纽人员疏散模型中的电梯运行参数,建议选取电梯荷载为14人、电梯额定最大速度为5 m/s、电梯加速度取软件默认的值为1.2 m/s2、电梯开关门时间为3 s,此为最优电梯运行参数。 本文利用Pathfinder软件建立了沙坪坝地下综合交通枢纽电梯与楼梯协同疏散人员疏散模型,研究了不同疏散场景下电梯运行参数对疏散时间的影响规律,主要得出以下结论: (1) 对于沙坪坝地下综合交通枢纽人员疏散模型而言,电梯运行参数对疏散时间的影响程度从大到小的排序为:电梯开关门时间、电梯额定最大速度、电梯荷载和电梯加速度。其中,电梯加速度对疏散时间几乎没有影响;在保证人员能够正常进出电梯的条件下,电梯开关门时间越短,疏散时间越少;电梯荷载越大,疏散时间越少;电梯额定最大速度越大,疏散时间越少。 (2) 根据电梯运行参数与疏散时间的关系曲线,可以得到疏散时间y与电梯开关门时间x1、电梯荷载x2和电梯额定最大速度x3的数学关系式如下: y=57.607×x1+2 083.6 (3) 电梯荷载和电梯额定速度对疏散时间的协同影响最大;电梯加速度和电梯速度对疏散时间的协同影响较小;电梯加速度和电梯荷载对疏散时间的协同影响最小。因此,建议沙坪坝地下综合交通枢纽中最优电梯运行参数的取值如下:电梯荷载为14人,电梯额定最大速度为5 m/s,电梯加速度为1.2 m/s2,电梯开关门时间为3 s。2 模拟结果与分析
2. 1 电梯运行参数对疏散时间的影响程度分析


2. 2 最优电梯运行参数分析




3 结 论

