基于混沌粒子群与Taylor算法的协同定位算法研究

康 婷，魏胜非

(东北师范大学物理学院，吉林长春 130024)

0 引言

在无线传感器网络应用中，节点的位置信息非常重要，按照是否需要测量节点间的距离或角度，将无线传感器网络节点定位方式分为2种，距离相关和距离无关。距离相关的定位算法主要有利用信号到达时间差[1]、接收信号强度[2]、信号到达时间[3]、信号到达角度[4]等信息测量相邻节点距离，这些算法定位精度相对较高[5]。

本文选择TDOA(time difference of arrival)定位方法，其核心是通过测量从未知节点发出的无线信号传播到已知坐标信息的多个信标节点之间的时间差来确定未知节点的位置。无线信号在传输时易受到很多因素影响，例如多径效应、远近效应和非视距传播等，致使TDOA测量值存在误差，所以转换成求解TDOA测量值构成的非线性双曲线方程组的问题[6]。目前有很多种求解的方法，如Fang算法[7]、Taylor算法[8]、PSO算法[9]等。

针对Taylor算法定位时存在受初值影响的情况，本文提出一种混沌粒子群与Taylor算法协同定位的方式：首先用混沌粒子群算法求解TDOA方程组，获得一个精度较高的未知节点的估计坐标值，然后将这个估计值作为Taylor算法的初值来迭代运算，最后完成对未知节点的坐标估计。

1 基于TDOA的节点定位方法

(1)

式中：c为电波传播速度；di,1为TDOA测量值；cni,1为测量时加入的噪声。

未知节点到信标节点之间的距离由以下公式计算可得：

所以

(2)

可以得到

ΔR=Ri-R1+cN=

(3)

当M≥3时，采用极大似然法求解未知节点坐标，由于Ri,1服从高斯分布，满足均值为Ri-R1、方差为α2，因此似然函数为

(4)

求当似然函数的值最大时，所得到的坐标值，等价于求解

即

(x,y)=arg{min[(ΔR-Ri+R1)T(ΔR-Ri+R1)]}

(5)

当此非线性函数方程值最小时，得到未知节点的估计值，若用解析法去求解会非常困难。因此，本文采用混沌粒子群算法求解，得到未知节点的初始坐标估计值。

2 W-CLSPSO算法

2.1 标准粒子群算法

PSO[11]算法是一种集群智能方法，它的提出是因为受到了鸟群捕食行为的启发，利用群体间的竞争与协作从而找到全局最优解，该算法容易实现，并具有快速的搜索能力。迭代时，粒子更新自己的位置和速度是通过跟踪个体极值pi,j和群体极值pg,j，更新方式如下：

vi,j(t+1)=w×vi,j(t)+c1×r1×[pi,j-xi,j(t)]+
c2×r2×[pg,j-xi,j(t)]

(6)

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(7)

式中：c1和c2为学习因子；r1和r2为0到1之间均匀分布的随机数；w为惯性权重。

粒子群优化算法的主要优点是容易工程实现，计算简便，但也有明显的缺点，容易陷入局部极值点、进化后期收敛速度慢、定位精度低等。

2.2 基于线性权重递减的混沌粒子群优化算法(W-CLSPSO)

为克服标准PSO这些缺点，将混沌的思想引入到粒子群算法[12]当中，本文选择Logistic混沌系统：

Zn+1=μZn(1-Zn)

(8)

式中μ为控制变量。

当μ值一定后，随机给定一个初始值Z0∈[0,1]就可以迭代出一个时间序列Z1，Z2，Z3，…。

由于混沌运动具有遍历性，因此混沌粒子群算法主要利用这个特性，以目前粒子群搜索到的最优位置为基础，产生一个混沌序列，把这个混沌序列中的最优位置粒子替代当前粒子群中任意一个粒子的位置[13]。

在粒子群算法中，惯性权重w对算法的挖掘能力和搜索能力有一定的控制能力。文献[14]通过实验证明，w随算法迭代次数线性减小时，算法具有很强的收敛性。

消费价格包括出口价格和分销成本，其中pj(φ)表示以本国货币表示的出口价格，τj表示本国出口到目的地j的冰山成本，εj表示本国与目的地j名义汇率[注]本文采用间接标价法，即εj越大说明本国货币相对于目的地(国)的货币升值。，λ表示企业参与垂直专业化程度，0≤λ≤1。假设产品质量越高则产品的分销成本越高，ηj表示目的地j的实际分销成本，wj表示出口目j的地的工资。代表性家庭对产品φ的需求为：

(9)

式中：wmax为初始惯性权重；wmin为终止惯性权重；t为当前迭代次数；tmax为最大迭代次数。

算法[15]步骤如下：

步骤1：对各个参数进行初始化设置。学习因子c1和c2，种群规模N，惯性权重wmax和wmin，混沌寻优的次数和进化的次数。

步骤2：随机产生粒子数为N的种群。

步骤3：利用式(6)、式(7)、式(9)更新粒子的位置、速度和权重。

步骤4：运用混沌对最优位置Pg=(pg1,pg2,pg3,…，pgD)进行优化。Logistic方程(8)的定义域为[0，1]，将Pgi(i=1,2,…，D)映射到此定义域中，其中：

Zi=(Pgi-ai)/(bi-ai),i=1,2,…,D

式中：ai和bi为第i维变量的取值范围。

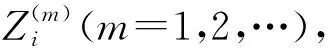
步骤5：从当前的种群中随机挑选出一个粒子用得到的最优解p*来代替。

3 Taylor算法

Taylor算法是一种递归算法，它将初始位置代入到算法，通过求解TDOA测量误差的局部最小二乘(LS)来改进。这种算法首先在未知节点的估计位置对其泰勒级数展开，对展开式中的二阶以上分量可以忽略不计，那么就有如下方程式：

h=GΔ+ε

(10)

式中：

Ri(i=1,2,…,M)为各个信标节点与未知节点的距离。式(10)的加权最小二乘解为

Δ=[ΔxΔy]T=(GTQ-1G)-1GTQ-1h

(11)

式中Q为测量值的协方差矩阵。

Taylor算法迭代循环的过程如下：首先选择ε当门限，用来判断是否可以结束此次迭代，然后通过比较迭代次数是否大于预先设定好的迭代次数，决定是否结束迭代，如果迭代结束，则此时的[x+Δx,y+Δy]将作为未知节点的坐标值。

4 W-CLSPSP/Taylor协同定位

Taylor算法是一种需要给定一个初值进行泰勒级数展开的算法，假如节点的真实值和估计值差距很大，将会导致算法不容易收敛，定位精度就会较低。所以使用W-CLSPSO初步估计未知节点的坐标，这样就保证了Taylor算法的初值具有了一定的精度，然后利用Taylor算法迭代计算，使得最终获得的坐标值具备较高的精度。

5 仿真结果及分析

为验证算法的有效性，用Matlab仿真平台对算法进行仿真，设节点分布在2 m×2 m的正方形区域内，在该区域部署6个节点，5个锚节点坐标分别为(0，0)，(0，2)，(2，0) ，(2，2)，(1，1)；1个作为未知节点，其真实坐标为(0.6，1.6)，单位是m。

算法初始化参数设置为：粒子群个数为20，学习因子c1=c2=1.494 45，最大迭代次数为500，其中标准PSO中w=0.7，CLSPSO中w=0.7，W-CLSPSO中wmax=0.9，wmin=0.4，Taylor算法的门限为ε=0.002，初始估计坐标为(0.6,1.6)，最大迭代次数30。节点测距时加入一个噪声N×randn，此噪声服从正态分布，单位是m。3种粒子群算法的收敛图如图1所示。

图1 算法收敛图

与标准PSO和CLSPSO算法相比，W-CLSPSO算法大约经过100次迭代，就可以达到满意的解，说明该算法定位速度很快。

在相同条件下，对标准PSO、CLSPSO、W-CLSPSO 3种算法在不同噪声下进行200次坐标估计，求平均估计坐标(x,y)，如表1所示，其RMSE=[(x-x0)2+(y-y0)2]1/2，如图2所示。

表1 PSO、CLSPSO、W-CLSPSO 3种算法的估计坐标

m

图2 PSO、CLSPSO、W-CLSPSO3种算法估计坐标的均方差比较

通过表1和图2可以看出，当噪声指数在0.1 m以下时，3种算法的RMSE值差别很小，在噪声指数N增大的过程中，W-CLSPSO算法的RMSE比PSO和CLSPSO算法都要小，实验表明，W-CLSPSO算法相比于其他两种算法，具有更好的定位精度和收敛性。

在相同条件下对Fang算法、Taylor算法和W-CLSPSO以及W-CLSPSO/Taylor协同算法在不同噪声下进行200次坐标估计，求平均估计坐标(x,y)，如表2所示，RMSE如图3所示。

表2 Fang、Taylor、W-CLSPSO、W-CLSPSO/Taylor4种算法的估计坐标 m

图3 Fang、Taylor、W-CLSPSO、W-CLSPSO/Taylor4种算法坐标估计的均方差比较

通过表2和图3可以看出，当噪声指数在0.15 m以下时，4种算法的RMSE值差别很小，在噪声指数N从0.15 m增大的过程中，W-CLSPSO/Taylor算法的RMSE明显小于其他3种算法，实验表明，W-CLSPSO/Taylor算法对坐标估计具有较高的精度。

6 结束语

在无线传感器网络中，针对TDOA定位方式，Taylor算法容易受初值影响较大致使节点定位精度低、后期不容易收敛等缺陷，提出了一种W-CLSPSO与Taylor算法协同定位的方式。经实验表明，W-CLSPSO/Taylor算法与其他定位算法相比拥有其明显的优势，极大提高了定位精度和全局搜索能力，为无线传感器网络的定位问题提供良好的参考价值。