基于零相位数字带通滤波的旋转机械不平衡量提取方法

荣 锋，黄 晨，郭翠娟，董攀浩

(1.天津工业大学电子与信息工程学院,天津 300387;2.天津工业大学，天津市光电检测技术与系统重点实验室,天津 300387)

0 引言

由于转子材质不均，形状不对称等因素，旋转机械在运行中通常会产生不平衡现象，导致机械振动、磨损，降低使用寿命[1]。为了消除这种情况，必须对转子实施动平衡[2]。动平衡操作即在适当的角度添加相应配重以抵消不平衡，但前提是要精确地获取不平衡的相位和幅值，即不平衡量。如何准确获取不平衡量是动平衡成功与否的关键。

由于转子不平衡产生的振动响应与转速同频，因此，通常同时采集转速和振动信号，以转速信号作为参考来获取与之同频的振动信号，然后通过各种分析方法提取不平衡量。目前，不平衡量的提取方法主要有时域提取法、频域提取法以及时频分析法。时域提取法主要采用硬件转速跟踪滤波法[3-4]，陶利民等[3]提出采用开关电容窄带通跟踪滤波电路提取不平衡信号，该方法具有转速跟踪滤波性能良好的特性，但需要专门的硬件滤波电路支持；频域提取法主要采用FFT基频提取法[5-7]，胡庆翰等[6]提出采用FFT实现高精度提取不平衡振动信号，但必须对信号整周期采样才能获取准确相位[5,7-8]，由于转速波动是客观存在的[3-4]，所以信号整周期采样实现困难；时频分析法是以经验模态分解理论[9-11]为基础提取不平衡量的方法，虽然同时适用于平稳和非平稳信号，但存在实现过程过于复杂，操作不够简单等问题。

基于以上方法的不足，本文提出一种基于零相位数字带通滤波的旋转机械不平衡量提取方法，该方法属于时域提取法，既不需要专门的硬件跟踪滤波电路，也不必对信号整周期采样，操作简单、容易实现。同步采集转速和振动信号，首先对振动信号零相位滤波，无相位差地滤出与转速同频的不平衡信号，然后由转速脉冲信号标定不平衡信号初相位，最后计算多周期不平衡相位、幅值的算术平均值，即可得到不平衡量信息。

1 方法原理

1.1 零相位滤波器原理

通常，无论是模拟滤波器还是数字滤波器，对信号进行时域滤波后都会引起相位的偏移，零相位滤波是为了解决此种问题的一种数字滤波技术。通过该技术构建的零相位滤波器，其系统函数的相位响应为零，即信号通过该滤波器后，不会产生相位变化[12-15]。对于滤波后需要保持信号相位的信号处理过程，零相位滤波无疑提供了一种绝佳的解决方法。

零相位滤波器实现的方法[12]是：首先按需求设计相应的数字滤波器，设输入的数字信号序列为x(n)，输入序列x(n)先按顺序滤波(Forward filter)，然后将滤波结果y1(n)翻转后得到序列y2(n)，再次通过滤波器(Reverse filter)，将滤波结果y3(n)翻转后(Reverse)输出，即得到精确的无相位失真的输出信号y(n)。滤波原理如下：

y1(n)=x(n)*h(n)

(1)

y2(n)=y1(N-1-n)

(2)

y3(n)=y2(n)*h(n)

(3)

y(n)=y3(N-1-n)

(4)

滤波过程对应的傅里叶变换的频域表达式为：

Y1(ejω)=X(ejω)H(ejω)

(5)

Y2(ejω)=e-jω(N-1)Y1(e-jω)

(6)

Y3(ejω)=Y3(ejω)H(ejω)

(7)

Y(ejω)=e-jω(N-1)Y3(e-jω)

(8)

由式(5)～式(8)整理得：

Y(ejω)=X(ejω)|H(ejω)|2

(9)

由式(9)可知，滤波输出Y(ejω)与输入X(ejω)之间只有幅度增益关系，在全频带不存在相移。所以理论上零相位滤波器可实现无相位失真滤波。然而滤波过程中序列需要时域上翻转，且客观上时间不可倒流，故该滤波器不具有物理可实现性，所以它只能通过数字滤波器来实现。

1.2 零相位数字带通滤波提取不平衡量方法原理

转子不平衡振动信号是与转速同频的振动信号，是单频的正弦波信号，不平衡量位于振动信号的峰值点处。为了获取不平衡量，本文提出一种零相位数字带通滤波提取不平衡量方法。首先，在稳定转速下同步采集转速、振动信号，根据转速数据计算平均转速；然后构建中心频率为转频的零相位带通滤波器，无相位差地滤出不平衡振动信号，由于振动信号与转速信号时间上同步，即具有相位一致性，故可将转速脉冲最低点作为初相位点标定不平衡振动信号，之后计算不平衡振动信号各周期峰值点的相位和幅值；最后，通过计算相位和幅值的算数平均值，即可得到最终的不平衡量。

本方法的总体流程图如图1所示。

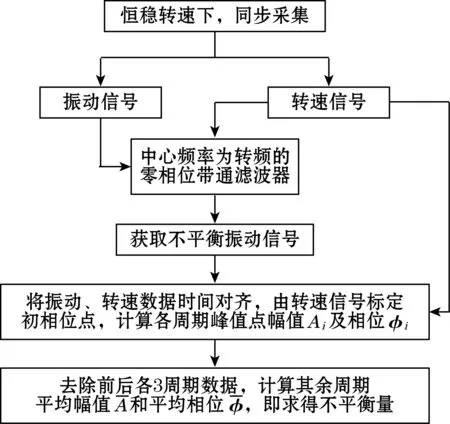
图1 总体流程图

具体实现的关键步骤如下：

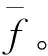
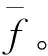
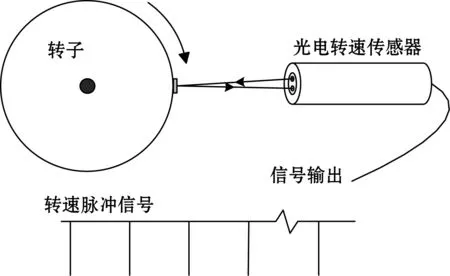
图2 光电转速传感器原理示意图

数字滤波器分为无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)2种，在设计滤波器时需根据其特性择优选择。IIR滤波器保留模拟滤波器的的优点，幅频特性好，但存在相位失真；FIR滤波器相频特性较好，可以实现线性相位，但在相同指标下阶数比IIR高得多。IIR滤波器具有优良的幅值滤波特性，零相位滤波器可以完美弥补IIR滤波器相位失真的不足，结合二者优势滤波能得到更准确的不平衡幅值和相位，故使用IIR滤波器构建零相位滤波器。而IIR中的巴特沃斯型滤波器通带平坦幅度最大，能更真实地滤出原信号的幅值信息，选用巴特沃斯型滤波器作为本方法的原型滤波器。

因为在实际信号采集中，不可避免地夹杂转频信号高次谐波频率及噪声信号的干扰，所以带通滤波器的带宽应尽量窄，本方法的滤波器带宽设置为1/5倍的信号频率，零相位数字带通滤波器采用三阶巴特沃斯带通滤波器。

(3)将振动信号通过滤波器，得到与转速同频的不平衡信号，然后将其与转速信号时间对齐，求取不平衡信号波形各周期的不平衡量。图3为各周期不平衡量计算方法示意图。

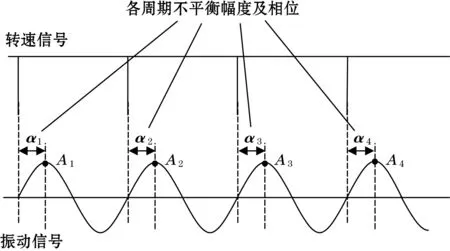
图3 各周期不平衡量计算方法示意图

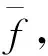
(10)

再获得第i周期峰值的幅度Ai，即得到了不平衡信号在该周期的不平衡量信息。

(4)最后求取各周期不平衡量的算数平均值，得到最终的不平衡量。

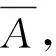
(11)

(12)

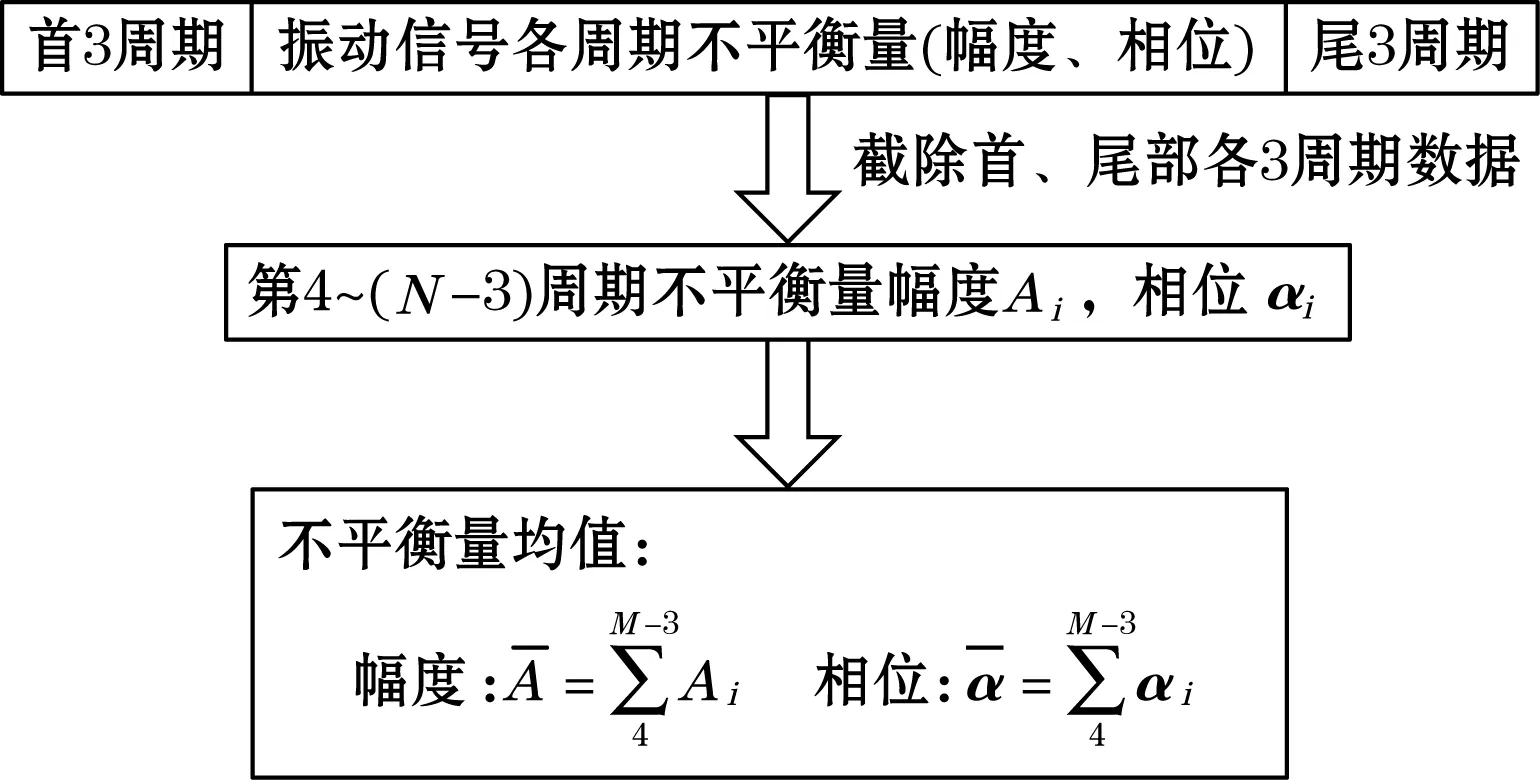
图4 计算不平衡量算术平均值流程图

本方法不需要对信号进行整周期采样，但在计算平均转速和不平衡量时需要多个周期的波形数据，设采样时间为T，不平衡信号周期T0，二者需满足T≥7T0(T⊂R+)，即至少有一个周期的有效数据。综合计算量和运算时间考虑，采样时间T的范围设定为12T0≤T≤26T0(T⊂R+)。

2 仿真

2.1 零相位滤波器仿真

零相位滤波器能够实现信号无相位差滤波。为了验证零相位滤波器效果，设计普通IIR低通滤波器和零相位IIR低通滤波器进行对比仿真实验。

使用的仿真信号为叠加了随机噪声的单频信号，信号频率为20 Hz，初相位为0°。信号的解析表达式为：x(t)=sin(40πt)+0.1×randn(1,N)。信号采样率为1 024 Hz，采样点数1 024点。设计采用三阶IIR低通滤波器，通带截止频率设置为30 Hz。将仿真信号依次输入普通IIR低通滤波器和零相位IIR低通滤波器，由图5的滤波结果对比图可以看出，通过普通IIR低通输出信号产生明显的相位偏移，而通过零相位IIR低通滤波器的输出信号与原始信号波形重合，没有相位偏移，证明零相位滤波器可以实现无相位差滤波。

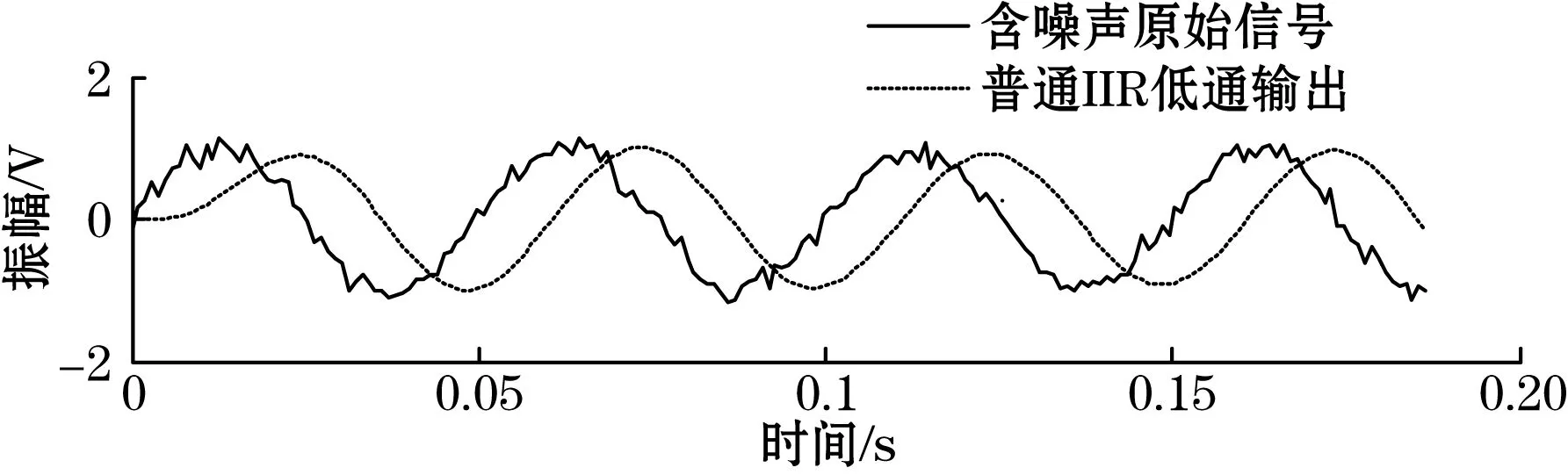
(a)普通IIR滤波器输出

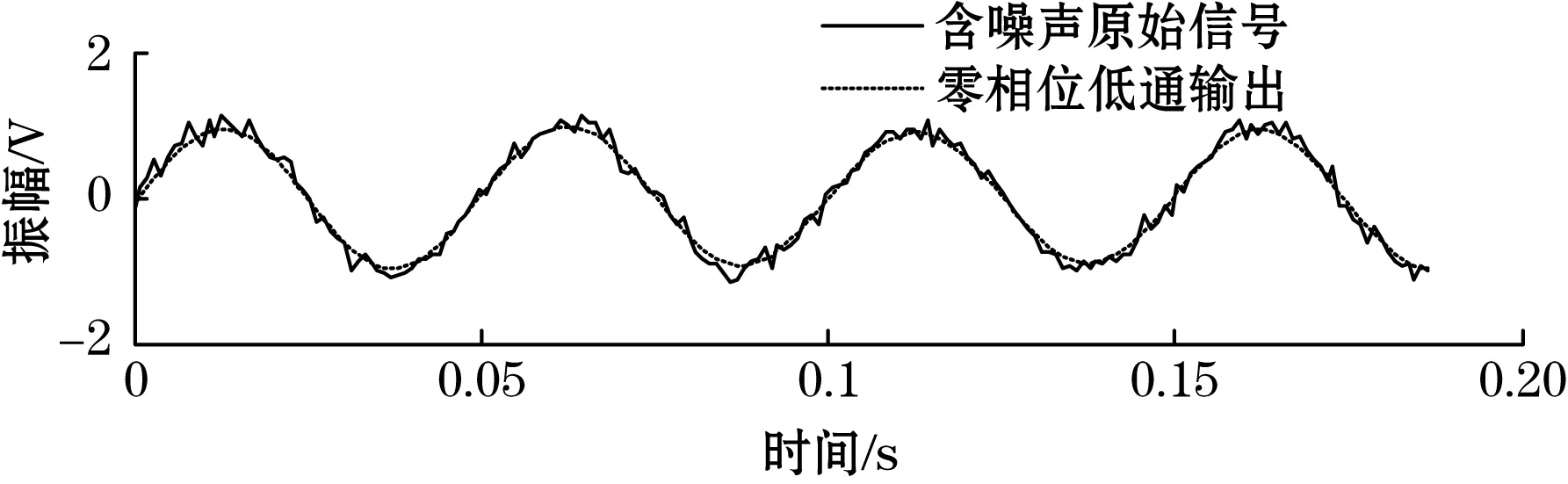
(b)零相位IIR滤波器输出图5 滤波结果对比图

2.2 本文方法仿真

为了验证本文提出方法提取不平衡量的效果，构造了仿真信号进行仿真试验。仿真转速信号脉冲方向向下，频率为20 Hz，幅值为5 V，起始脉冲相位为0°。仿真不平衡振动信号频率为20 Hz，初相位为180°，幅值为1 V。考虑到振动信号采集时包含其他频率分量和噪声干扰，仿真振动信号中叠加40、200 Hz谐波信号及随机噪声作为干扰信号，振动信号解析表达式为

sin(40πt+π)+sin(80πt)+0.5×sin(400πt)+
0.2×randn(1,N)

不平衡量位于不平衡信号峰值点处，不平衡振动相位=振动初相位(180°)+90°=270°，不平衡幅值为1 V。

本方法能够实现非整周期采样信号的不平衡量提取。信号的采样率设置为10 240，采样周期点数为10 000点。信号整周期点数为10 240/20=512点，采样周期与信号周期比值为10 000/512=19.53，为非整周期采样。

本方法的仿真结果如图6所示。结果表明，本方法可以很好地提取叠加信号中的不平衡信号，准确定位不平衡量。获取的不平衡相位为270.468 8°，幅值1.003 7 V。相位误差0.468 8°，幅值误差为0.003 7，不平衡量提取效果比较理想，证明方法的有效性。

(a)振动信号(仿真)

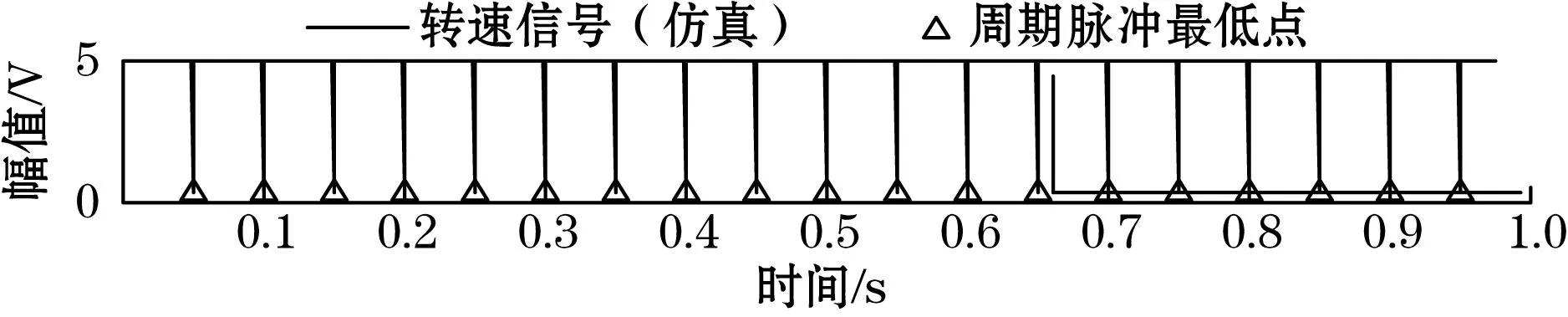
(b)转速信号(仿真)

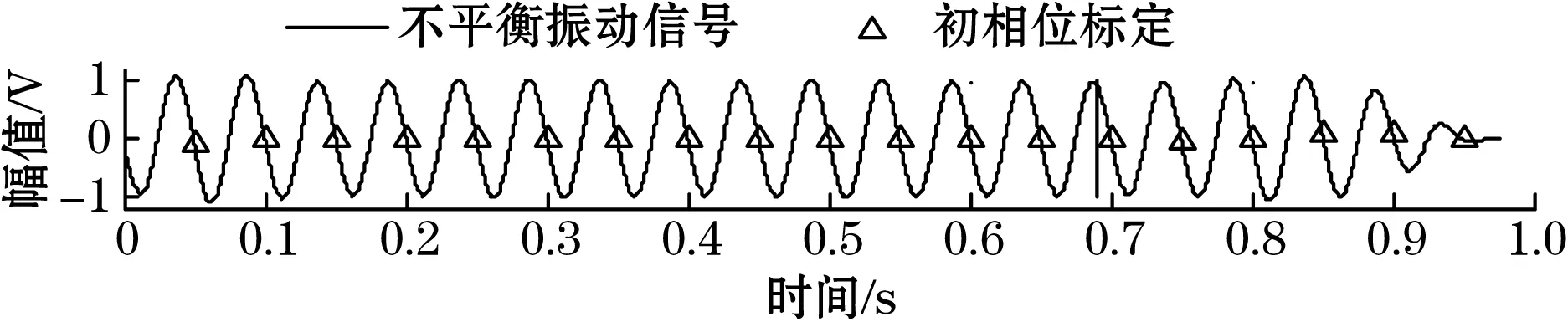
(c)滤波后不平衡振动信号

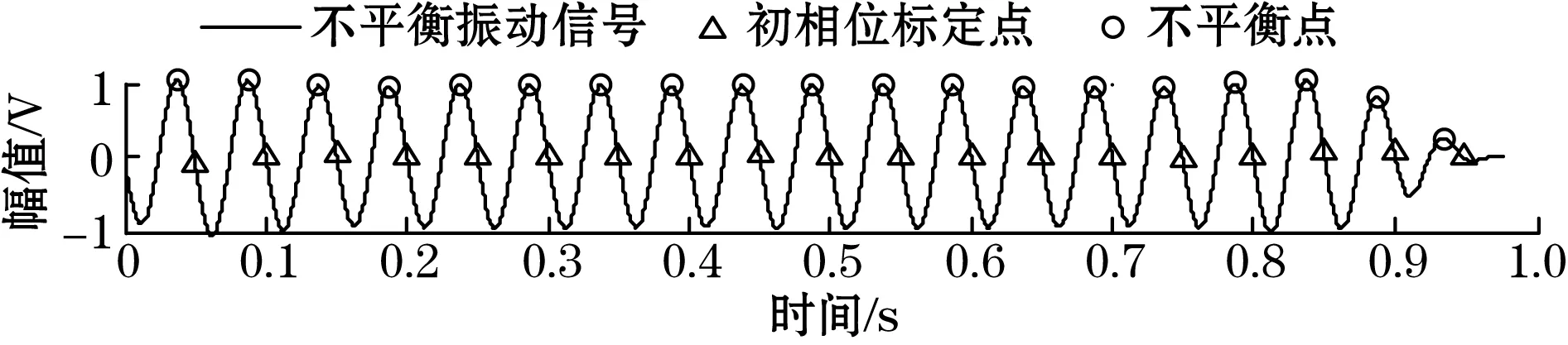
(d)不平衡量：相位为270.468 8°，幅值为1.003 7 V图6 仿真信号不平衡量提取

本方法可以实现对信号非整周期采样下，不平衡幅值和相位的精确提取。如图7所示，对采样周期与信号周期比值在19.5～20范围内进行了不平衡量仿真提取试验，仿真结果表明：FFT提取法只有在周期比为20，即信号整周期采样下才能准确获取幅值和相位信息，非整周期采样下得到的不平衡幅值和相位信息失真严重，且随着周期比偏离整周期数越大，失真程度越高。幅度失真最大超过30%，相位失真最大超过80°，而本方法在整周期、非整周期采样下均能准确、稳定地提取不平衡幅值和相位。

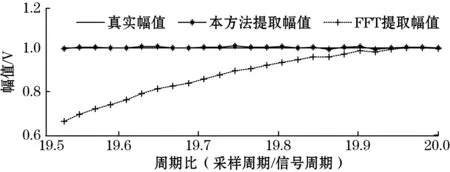
(a)幅值提取对比图

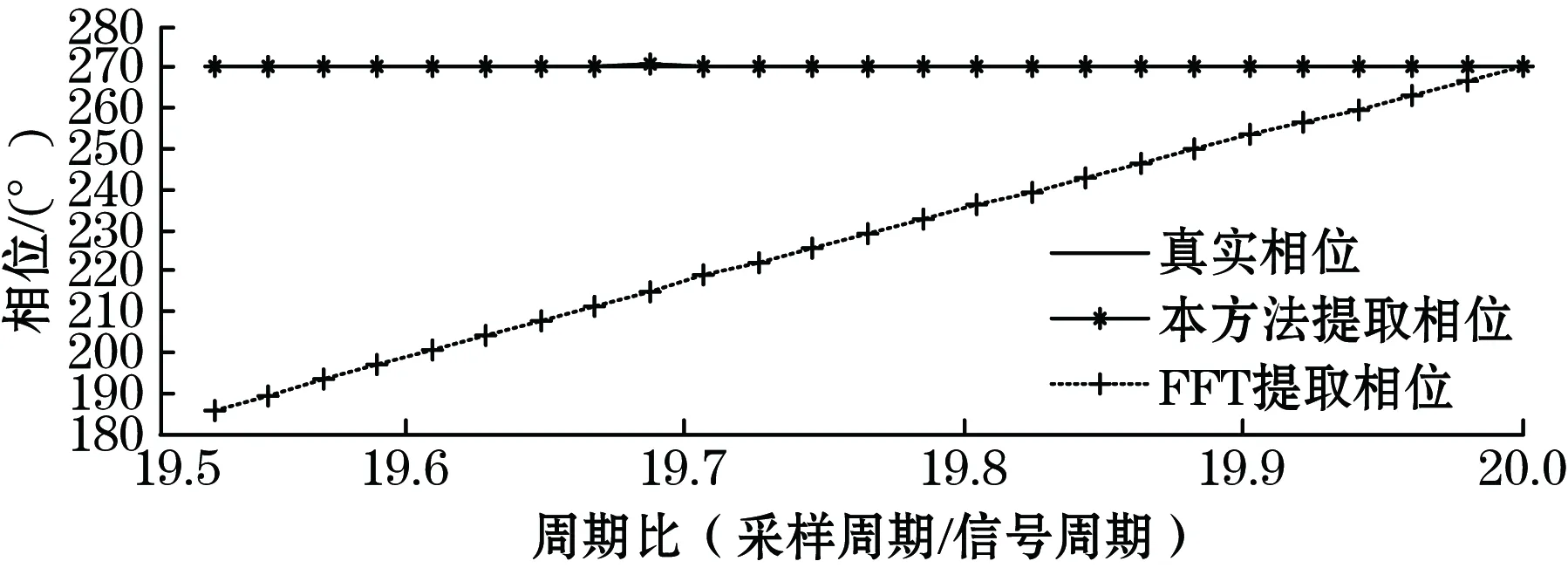
(b)相位提取对比图图7 FFT与本方法提取效果对比图

3 实测信号验证与分析

为了验证本方法用于转子动平衡的实际效果，在机械转子实验平台进行了不平衡量提取试验并进行了单面动平衡校正。实施过程如下：振动信号测量采用加速度振动传感器，转速信号测量采用光电式转速传感器，将光电转速传感器的反光标签处作为相位零点，测量转速设定为1 140 r/min。信号采样率为10 240 Hz，采样点数为10 000点，采样周期-信号周期比为18.55，为非整周期采样，动平衡操作流程为：

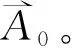
(a)振动信号(实测)

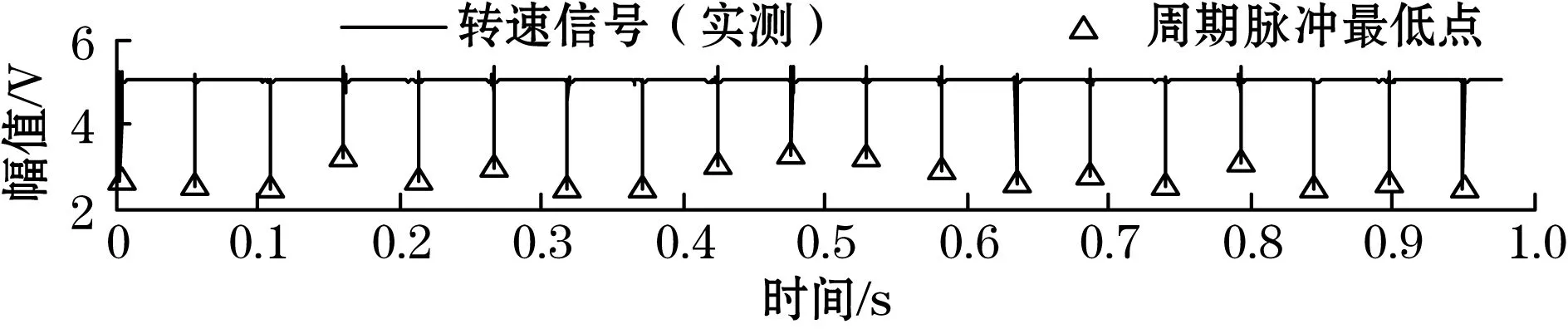
(b)转速信号(实测)

(c)滤波后不平衡信号

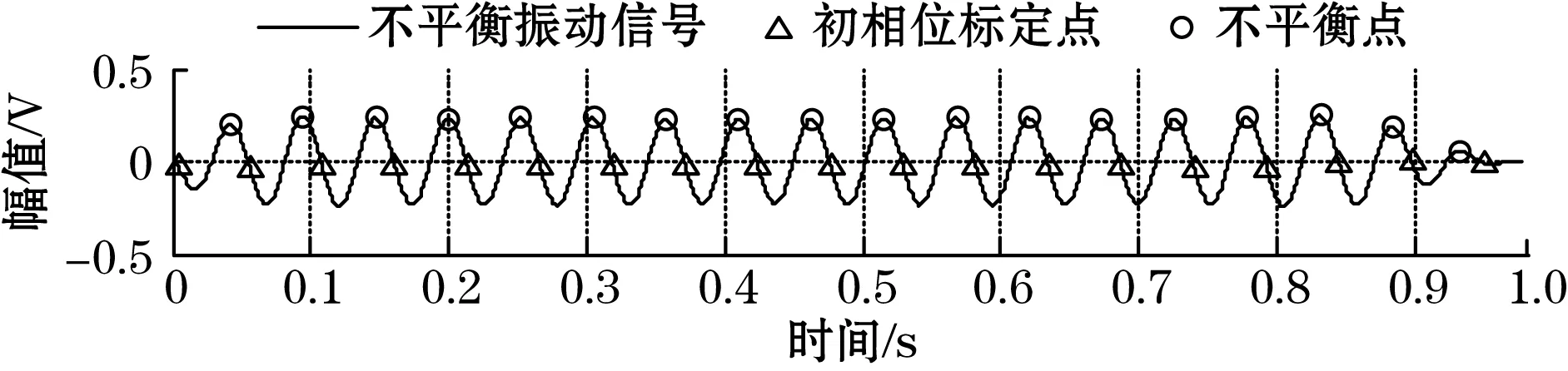
(d)不平衡量：相位为269.058 6°,幅值为0.233 54 V图8 实测信号原始不平衡量

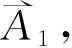
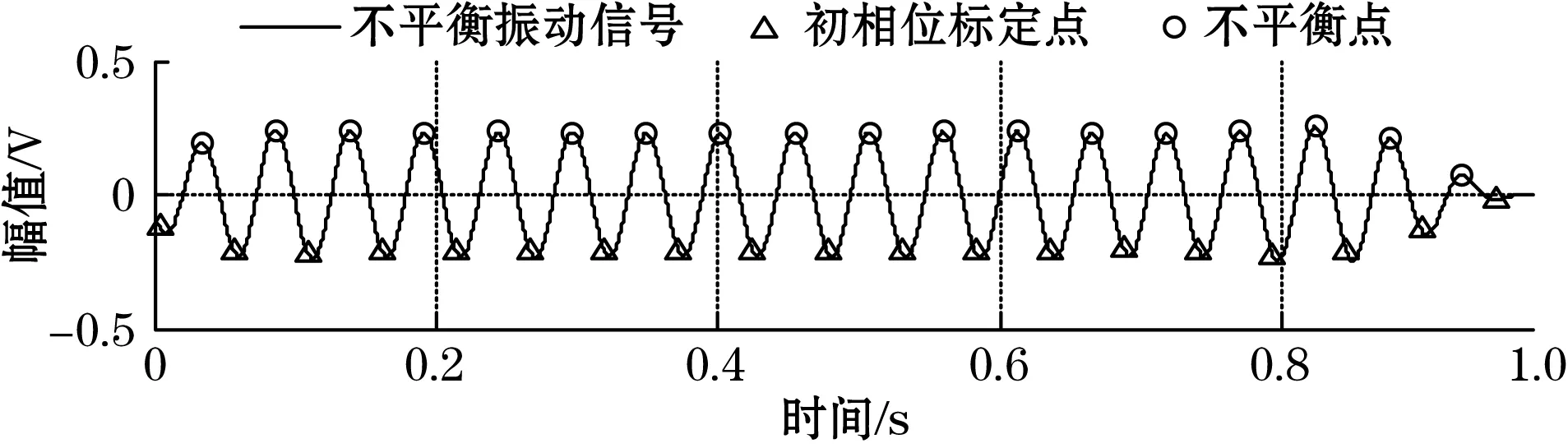
不平衡量：相位为210.807 8°,幅值为0.233 72 V图9 实测信号加试重不平衡量

(13)

将本方法提取的不平衡量代入公式计算得到原始不平衡质量为5.842 3 g，不平衡相位为269.058 6°，引起原始不平衡振动的真实质量为6 g，角度为270°，所以不平衡质量误差为0.157 7 g，相位误差为0.941 9°。

(3)第三次，根据不平衡量的计算得到的质量值对转子在相反的角度进行质量补偿后，测量剩余不平衡量，如图10所示，不平衡角度为24.414 4°，幅值下降至0.033 216 V。动平衡效率达到85.78%，有效消除了大部分的原始不平衡振动量。

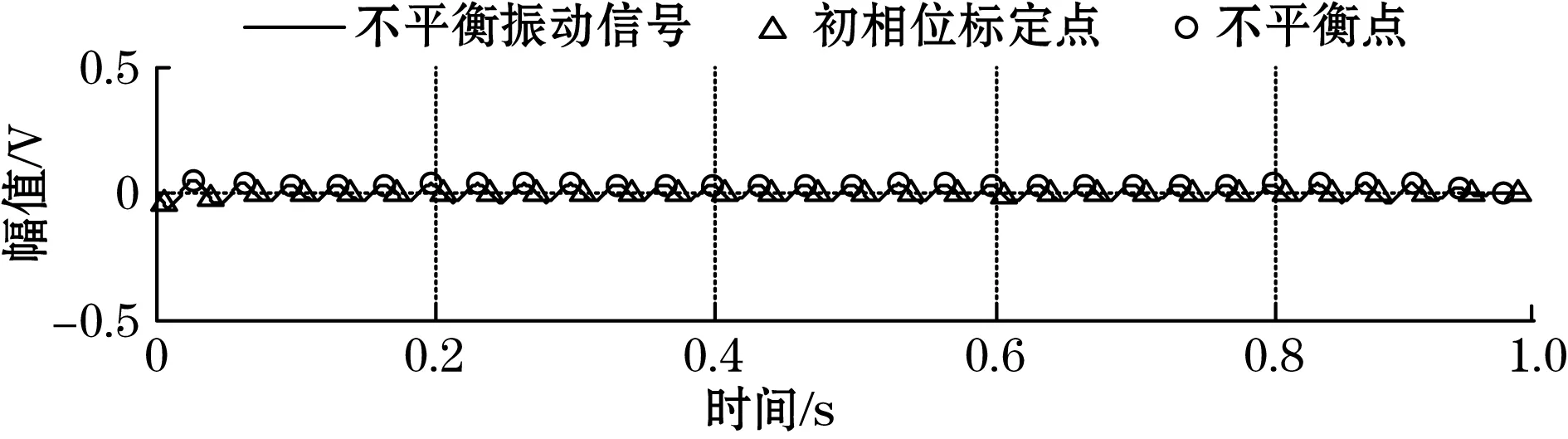
不平衡量：相位为24.414 4°,幅值为0.033 216 V图10 动平衡后剩余不平衡量

在转速范围600～4 800 r/min下，设置不平衡量为相位270°，共了进行8次动平衡实验，相位提取曲线如图11所示，可以看出，采用本方法提取的不平衡相位误差较小，误差在2°以内，提取的相位稳定度好。

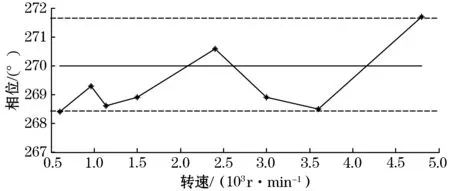
图11 不同转速下不平衡相位提取折线图

实施单面动平衡校正后，平衡结果如表1所示。实测结果表明：采用本方法提取的不平衡量在进行动平衡后，平衡效率大于80%。综合来看，本方法提取不平衡量稳定性好，准确度高，具有较高的工程实用价值。

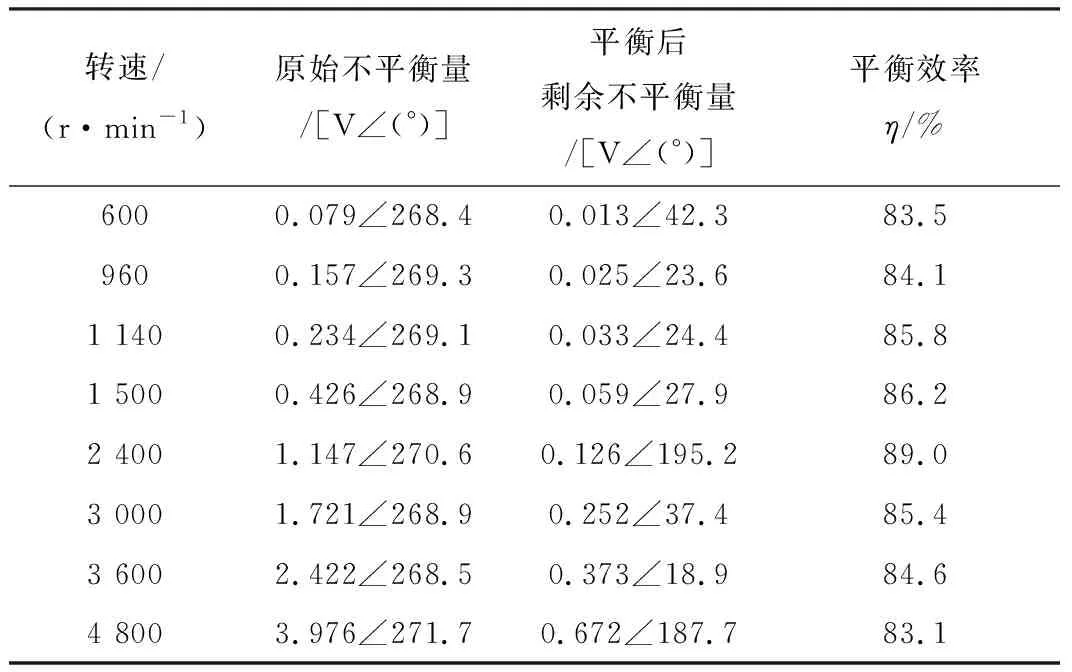
表1 本方法不同转速下的动平衡效果

4 结束语

本文针对FFT频谱法难以从非整周期采样的信号中提取转子不平衡量的问题，提出了一种基于零相位数字带通滤波的旋转机械不平衡量提取方法。本方法的优点为：

(1)采用零相位数字滤波器，无需专门的硬件跟踪滤波电路即可实现转速跟踪滤波；

(2)克服了传统FFT基频提取法提取相位时需要对信号整周期采样的限制，能够在非整周期采样下准确提取旋转机械不平衡量；

(3)本方法原理简单，容易实现。

实测结果表明：采用本方法提取的转子不平衡量定位准确，相位提取误差小于2°，提取的不平衡量对转子实施动平衡校正后平衡效果显著，转子剩余不平衡量较小，平衡效率大于80%，重复性能较好，可以实现高精度的动平衡测量。拓展了零相位滤波在转子动平衡领域的应用，具有较高的工程实用价值。