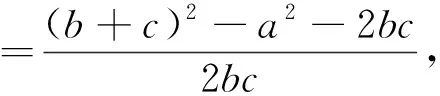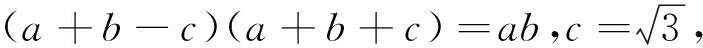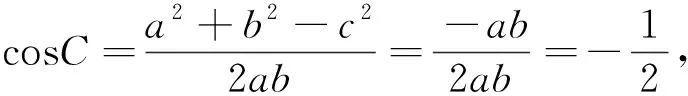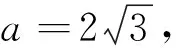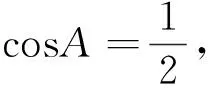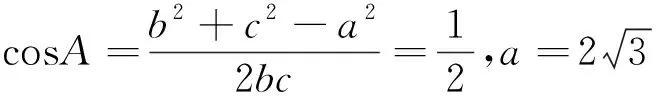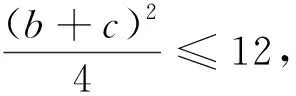余弦定理 不得不知的奥秘
2019-02-21
福建省德化第一中学 (邮编:362500)

1 乘法公式价值高,模型构造威力显
观察角A的余弦公式,发现分子为b2+c2-a2,变形可得(b+c)2-a2-2bc,由此可利用乘法公式设计构造出平方差公式,再变形构造出余弦公式.命题者不仅可以考查学生是否能够熟练掌握公式,还可考查学生变形构造公式的能力.
例1已知:在△ABC,角A、B、C所对的边分别为a、b、c,(sinB+sinC-sinA)(sinB+sinC+sinA)=sinBsinC,求角A的余弦值?
解析利用正弦定理将角转化为边可得:(b+c-a)(b+c+a)=bc.
利用平方差公式可得:(b+c)2-a2=bc即b2+c2-a2=-bc.
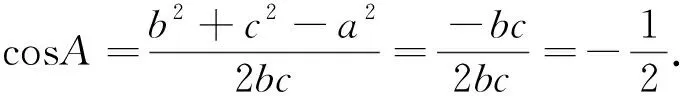
2 平方关系真给力,夹角范围确定易
观察角A的余弦公式,发现分子为b2+c2-a2,比较分子与0的大小,可得:
当b2+c2>a2时,cosA>0,此时角A为锐角;
当b2+c2=a2时,cosA=0,此时角A为直角;
当b2+c2 命题者不仅可以利用三边平方的大小关系来判断角的范围,还可进一步用来确定三角形的形状. 例2在非等边△ABC中,角A、B、C所对的边分别为a、b、c,a为最大边,如果sin2(B+C) 解析由于sin(B+C)=sin(π-A)=sinA, 所以sin2(B+C) 由正弦得:a2 又因为△ABC非等边,且a为最大边,所以A>60°, 则有60° (1)求cosB; (2)若a+c=6,三角形的面积为2,求b. (四)在国内产能过剩的情况下,中国光伏“走出去”的步伐将进一步加快,以产融结合、厂商租赁等模式将产能向西方国家以及“一带一路”沿线国家转移,将成为中国未来光伏产业持续健康发展的现实选择。 所以sinB=4(1-cosB), 又sin2B+cos2B=1, 整理得17cos2B-32cosB+15=0, 解得b2=4,即b=2. (2)当三角形的周长为6,求其面积. (2)由于三角形的周长为6,且b=2,所以 例5△ABC内角A、B、C所对的边分别为a、b、c,已知三角形的两边a、b为一元二次方程的x2-3x+1=0的两个根且夹角C为60o,求三角形的周长. 解析由a、b为一元二次方程的x2-3x+1=0的两个根,可得a+b=3,ab=1, 解析由(a+b-c)(a+b+c)=ab,得(a+b)2-c2=ab,则有a2+b2-3=-ab, 即3-ab=a2+b2. 由基本不等式可得:3-ab=a2+b2≥2ab,得ab≤1(当且仅当a=b取等号). 当ab取得最大值1时, (1)求角A; 得2sinCcosA=sin(A+B)=sin(π-C)=sinC, 利用余弦定理丰富的内涵为命题者提供各种各样的设计思路,学生也可从命题设计的思路来对定理的学习与研究,丰富自已的解题经验和发展自已的思维.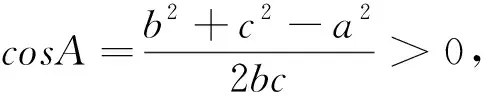
3 周长面积“影子”现,相互依存和谐见
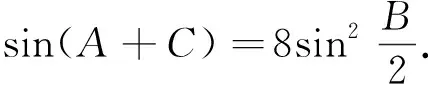
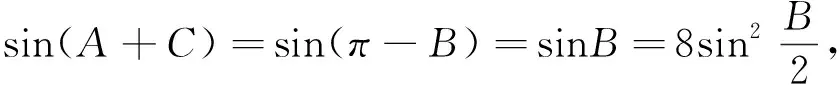
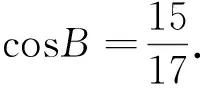
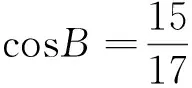
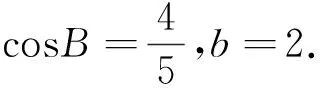
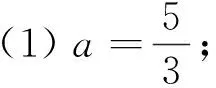
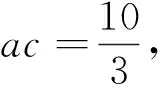
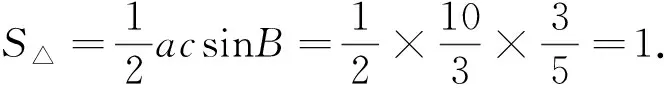
4 和、积合作有情意,两根关系来设计
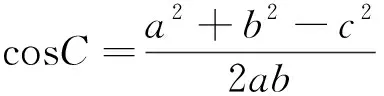
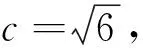
5 加法乘法巧联系,最值获取最省力