基于动态等效刚度的平面柔性铰链建模与分析

应玲君， 赵荣珍， 马德福， 唐小斌

(兰州理工大学 机电工程学院, 兰州 730050)

在刚性机构中，运动副间隙带来的运动轨迹偏离和关节碰撞冲击等问题严重影响着机构的工作性能和使用寿命[1]。而采用柔性铰链替代传统运动副的柔顺机构则能有效地降低此方面的影响，正确地传递运动和力，还具有：结构轻便，易于一体化加工，能简化装配过程；无磨擦，从而能消除磨损、噪声和振动；无需润滑，可避免污染等[2]优点，因此被广泛应用于微机电、光学、航空航天等领域[3-4]。柔顺机构还具有回弹特性，在避免间隙影响的同时也能起到良好的抑振效果[5]。其中，设计柔顺机构的关键在于设计出符合运动要求的柔性铰链。

所谓柔性铰链，它是一种利用自身的弹性变形在相连的刚体间传递力或运动的弹性元件[6]。当前柔性铰链的设计多采用刚体代替综合法[7]，即先将相对复杂的刚性铰链分解成简单的运动副，再用具有相似功能的柔性片段替换刚性构件，最后将各柔性片段叠加整合成新的柔性铰链。针对这种传统柔性铰链，Rad等[8-9]通过在刚体间架设3个柔性转动副满足了三自由度柔性球铰的要求，并推导了铰链的刚度计算方程；Liu等[10]则对柔性转动副的切口结构进行了拓扑优化，基于去除材料的方法提高了转动性能。而平面溢出铰链[11](Lamina Emergent torsional，LET)作为一种由二维金属薄板平面加工而成，实现三维运动的新型柔性铰链，在拥有传统柔性铰链优点的同时进一步简化了其结构。Wilding等[12]在LET铰链内部加入一个反向弯曲的次级铰链，构成了一个体积小巧但能承受轴向力的新转动副；邱丽芳等[13]则展示了LET铰链易于变形的特点并对比了两种等效刚度分析方法的适用范围；基于LET铰链的大变形特性，Qiu等[14]和Fowler等[3]分别以两种不同的思路进一步扩大了铰链工作空间：Qiu将三个LET铰链进行了串联，在实现了大范围转动的同时降低了最高应力；Fowler则将16个柔性薄片进行了复杂的并联整合，达到了90°侧向弯曲的要求并分析了其配置参数对转角范围的影响。

目前新型柔性铰链的研究主要集中在单一转动副的实现及其结构性能优化，但对如虎克铰等多自由度的运动副仍采用“分解-替换-整合”的传统设计方法，即将多个柔性转动副物理叠加，结构臃肿复杂，尚未有构型轻便的多自由度铰链一体化解决方案。为此，本文基于LET柔性铰链的结构特点，欲进一步扩展其运动形式，提出一种能实现虎克铰功能的平面柔性铰链，建立动态的铰链等效刚度模型，并根据其刚度变化特性进行实例仿真验证。

1 平面柔性铰链设计及其自由度分析

1.1 虎克铰结构分析

传统的虎克铰如图1所示，它由一个十字轴和两个叉形铰链座组成。叉形铰链座绕着十字轴实现空间两自由度的相对转动。其中，十字轴受到来自叉形铰链座的2个径向和2个轴向的约束。这8个接触副(虚约束含4个接触副)在运动中互相摩擦磨损，其产生的运动副间隙则会严重地影响铰链运动传递的准确性。

(a) 转动状态1(b) 转动状态2

图1 虎克铰

Fig.1 Hooker hinge

1.2 平面柔性铰链设计

基于变形LET铰链[13]的特点，本研究所建立的平面柔性铰链如图2所示，铰链上下矩形部分用于相邻构件的连接，为刚性区域，中间的环形部分产生变形，为柔性区域。如图2(a)所示，柔性区域绕转动中心弯折，刚性区域随之转动(等效于图1(a)的转动)。LET铰链通常只有这一个转动自由度[12-14]，而本文建立的平面柔性铰链因环形的结构特点，运动形式可进一步扩展为图2(b)形式：当转动中心绕z轴旋转θ角时，铰链发生偏转，刚性区域随之侧倾(等效于图1(b)的运动)。同时，环形结构保证了铰链各个偏转方向上的刚度不会存在较大差异，且结构简单便于加工制造。

(a) 弯折状态(b) 偏转状态

图2 平面柔性铰链

Fig.2 Plane flexible hinge

1.3 平面柔性铰链自由度分析

为验证图2所示铰链的运动形式，探究其变形性能，现对铰链的自由度进行分析。铰链各参数如图3所示。

为便于分析，将平面柔性铰链视作梁。故当坐标系处于平面柔性铰链质心时，铰链柔度矩阵λ可近似为等尺寸梁的柔度矩阵：

(1)

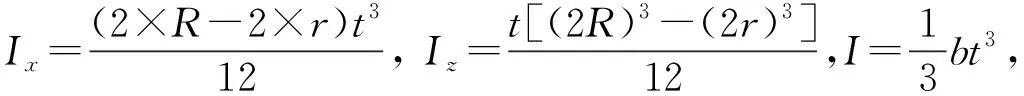
现给定参数如下：b=50 mm，l=275 mm，R=87.5 mm，r=60 mm，厚度t=1 mm。由于铰链工作主要依靠弹性变形，故材料选用弹性极限、疲劳极限较高且弹性迟滞较小的铍青铜，弹性模量E=128 GPa，泊松比μ=0.35，切变模量G=E/[2(1+μ)]=47.41 GPa。则可以得到各个柔度间的比值关系：

(2)

(3)

理论上柔性体具有无限个自由度。而从式(2)、式(3)所示的柔度比值关系中我们可以得出：在z方向上的平动柔度λtz远大于x和y方向上的平动柔度λtx和λty；绕着x轴和y轴的转动柔度λθx和λθy远大于绕z轴的转动柔度λθz。表明这三个方向的自由度具有更大的自由程度，即该平面柔性铰链主要具有tz、θx和θy三个自由度。而z方向的平动tz如图3所示，实际上是由铰链的柔性区域在yz平面内的弯曲微变形引起的，即tz由θx引发，铰链不具有传统意义上的z方向平动自由度。因此只需通过θx和θy两个方向的组合变形，铰链即可实现弯折和偏转，满足虎克铰两自由度的要求。

2 平面柔性铰链的动态等效刚度分析

在1.3小节的分析中，柔度、惯性矩等相关计算均采用了简化算法，并未详解。为进一步揭示铰链的变形特性，需对铰链不同位姿下的动态等效刚度进行更为精确的分析计算。

2.1 弯折时的等效刚度计算方法

假设柔性铰链在力矩T下发生总计角度为δ的弯折。如图3所示，现将铰链沿y轴方向划分成n个柔性微分片段dy，由于圆环中心圆孔的隔断，微分片段可分为连续的dy1和分离的两段并联关系的dy2两类，每个微分片段在力矩T下分别发生相应弯折，则δ为两类所有片段弯折角度之和：

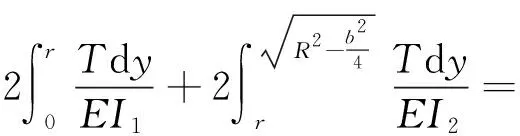
(4)

而力矩转角关系又可表示为T=kfδ，则此时平面柔性铰链的等效刚度为：

(5)

2.2 偏转时的等效刚度计算方法

图4所示是用于计算偏转时等效刚度的分析模型，当柔性铰链偏转θ角时，由于铰链中的矩形部分为刚性

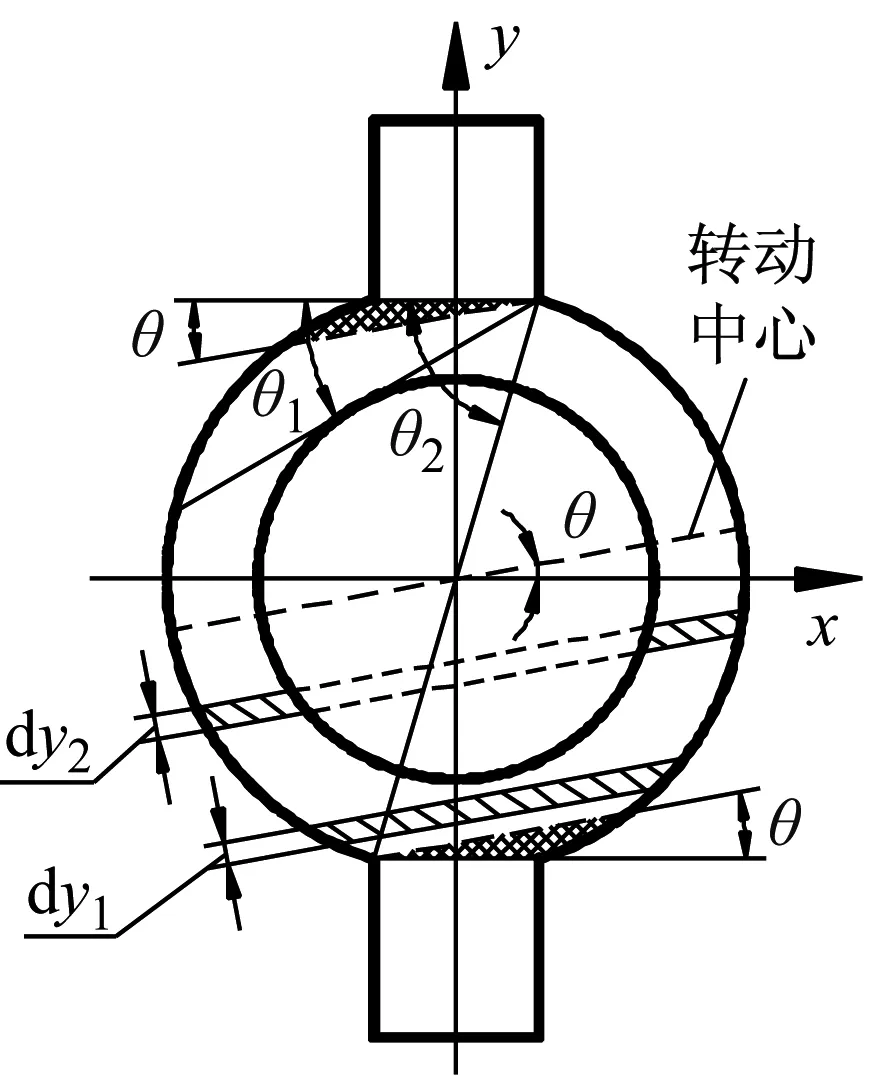
图4 偏转时的柔性铰链

区域，从而使柔性区域(圆环)中阴影部分也不参与变形，即铰链形成“刚性-柔性-刚性”的斜向串联式结构。同时柔性区域的面积随着偏角θ的增大而相应的减少。

按照2.1小节中的思路，沿转轴中垂线方向划分出两类微分片段，则图4模型的等效刚度分为如下两种情况：

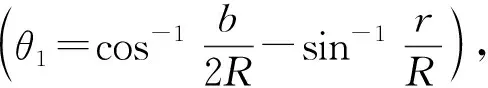
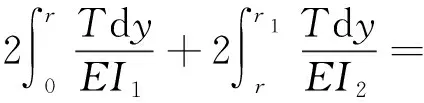
(6)

平面柔性铰链的等效刚度为：

(7)

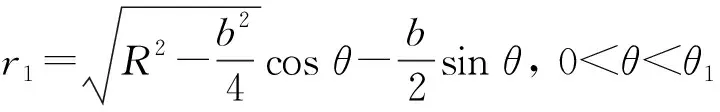
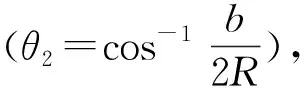
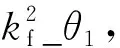
表1 五组平面柔性铰链参数表

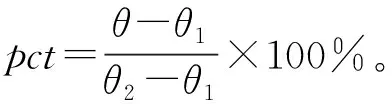
对新的p点重新拟合的结果如图6所示，可以发现五组曲线完全重合。这表明铰链的比例系数p与其偏转程度(偏角百分比pct)的关系存在一定共性，且不受

图5 偏角与比例系数的关系曲线

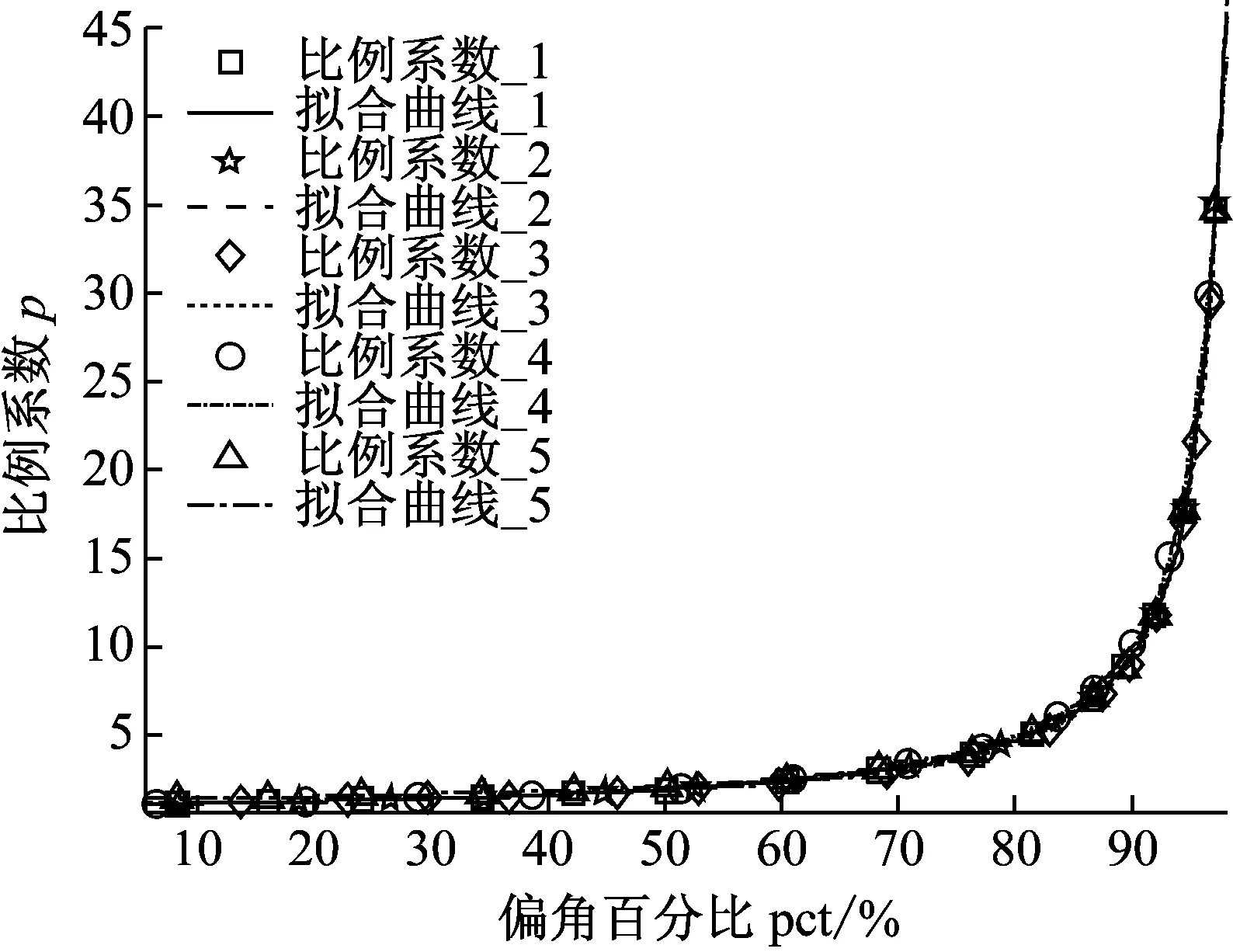
图6 偏角百分比与比例系数的关系曲线

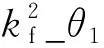
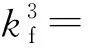
(8)

由式(5),(7),(8)可得平面柔性铰链的动态等效刚度计算公式为：

(9)

2.3 有限元仿真验证

为便于分析，去除各转角模型相应的刚性区域。对有限元模型连接刚性区域的两个端面分别施加10 N·m/rad的转矩，两端各产生转角θsim。如图7所示为θ=10°时的z方向变形云图，通过查看具体变形数值可计算出铰链两端的斜率，进而得到铰链的转角数值。据此方法可得到不同偏转角度下等效旋转刚度的仿真值。同时通过式(5)和式(7)可得到相应的理论计算值。两种途径得到的等效刚度值及其对比情况，如表2所示。

表2不同偏角下铰链等效刚度的理论值和仿真值及其误差

Tab.2Thetheoreticalandsimulationvaluesoftheequivalentstiffnessofhingesunderdifferentdeflectionanglesandtheirerrors

偏角θ/(°)理论值kf/(N·m·rad-1)仿真值ksim/(N·m·rad-1)误差/%06.556.793.64107.337.471.79208.338.31-0.31309.659.59-0.654011.4611.651.69

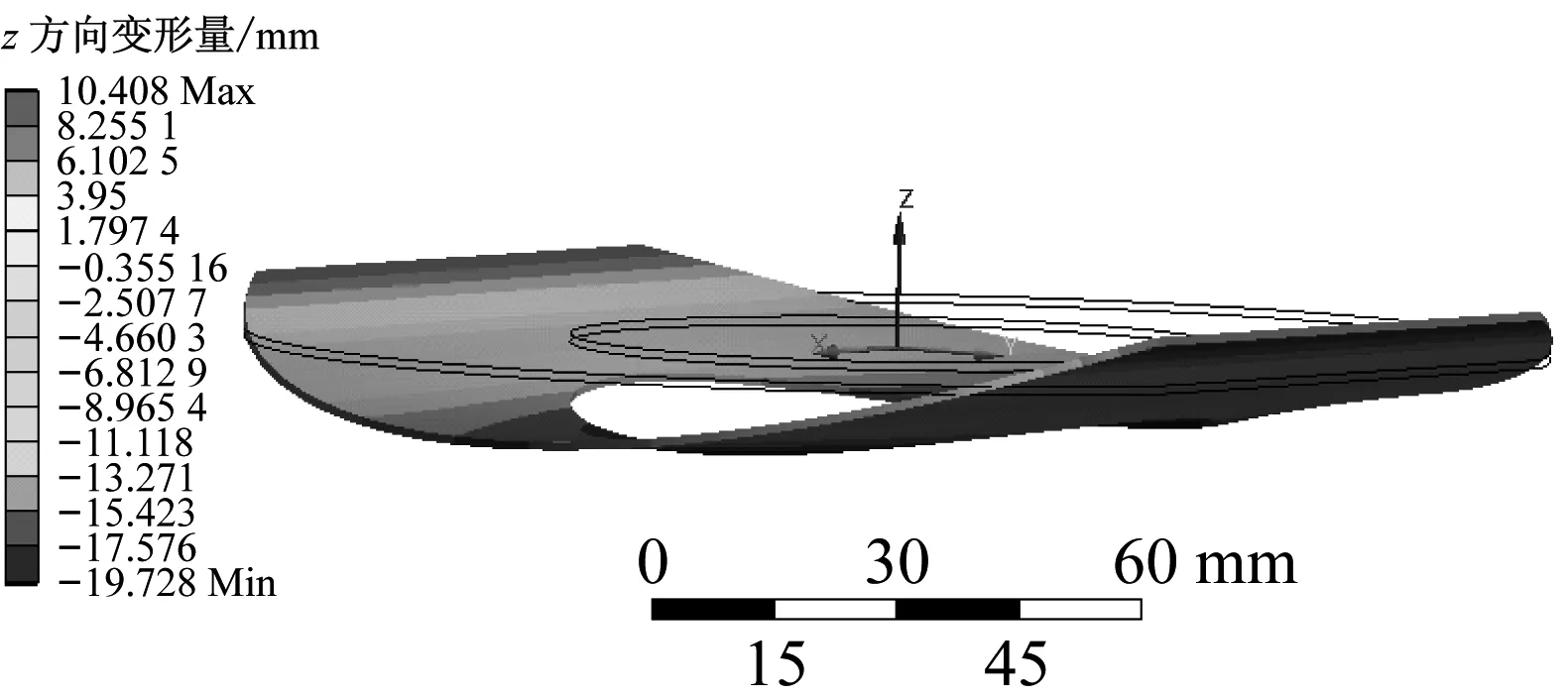
图7 偏角θ=10°时铰链的变形云图

由表2可知：在不同偏角下，铰链等效刚度的理论值与仿真值基本一致，其相对误差最大不超过3.64%，证明了刚度计算模型的正确性。

同理，可求得在极限偏角θ2=70 °时的最大工作应力为458.63 MPa，低于材料屈服极限1 035 MPa的一半，因而不会发生塑性变形。

3 平面柔性铰链的动态刚度特性分析

基于所建立的平面柔性铰链动态等效刚度计算模型，若要设计出满足性能要求的柔性铰链，仍需研究动态等效刚度的变化特点。但由式(9)较难直观地看出各参数与等效刚度之间的关系，由此我们对各参数逐一进行分析，进而为平面柔性铰链的应用提供理论依据。

3.1 铰链结构参数对等效刚度变化的影响分析

现取θ=0时进行刚度分析，如图8(a)，(b)，(c)，逐一改变各结构参数值，可以得到平面柔性铰链各参数和其等效刚度之间的关系，即：随着铰链圆环外径R、宽度b、厚度t的增大，内径r的减少，铰链等效刚度呈现上升趋势。其中，铰链等效刚度对厚度t的变化最为敏感，而矩形部分宽度b与刚度值关系的非线性程度最弱。

(a) 等效刚度与b的关系图(b) 等效刚度与t的关系图

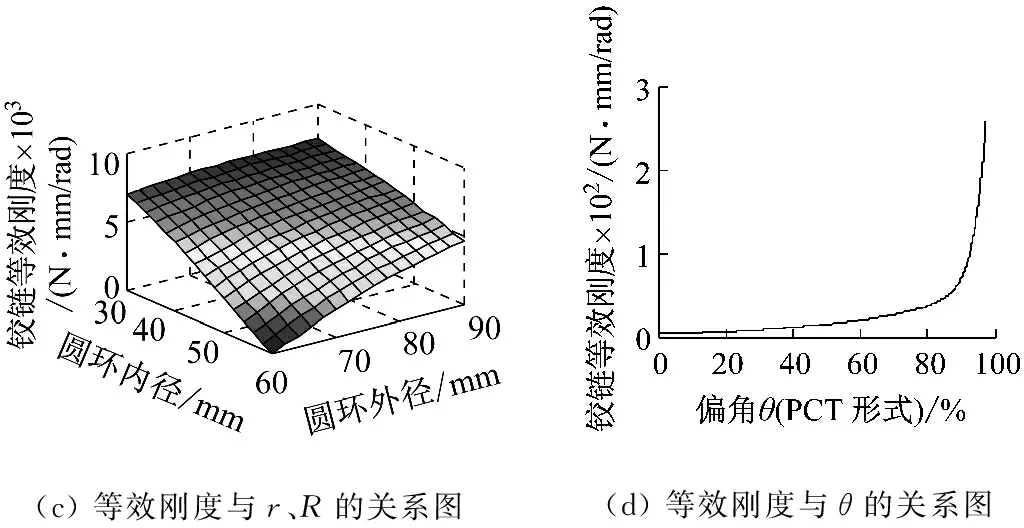
(c) 等效刚度与r、R的关系图(d) 等效刚度与θ的关系图

图8 铰链参数b、t、R、r及偏角θ与等效刚度的关系图

Fig.8 The relationship between the hinge parametersb,t,R,r,θand the equivalent stiffness

3.2 铰链偏角θ对等效刚度变化的影响分析

当柔性铰链各结构参数固定时，如图8(d)所示，我们可以得到铰链偏角与其等效刚度之间的关系：当偏角小于极限偏角的70%时，随着偏角的增大，等效刚度略微增大，且非线性程度较弱，基本呈线性关系；当偏角达到极限偏角的80%时，曲线非线性程度逐步增大；而90%以后则因接近铰链极限偏角，刚度值剧增，实现了铰链极限位姿的截止作用。

基于上述平面柔性铰链的动态刚度变化特点，对铰链的刚度应用特性进行分析。当铰链小范围偏转时，刚度基本不变，可实现虎克铰运动的传递；当含该铰链的实际机构位姿接近极限时，铰链刚度急剧增大，可对机构整体运动发挥截止作用；而当实际机构中同时采用多个平面柔性铰链时，因机构运动过程中位姿不断变化，各平面柔性铰链偏角θ值呈现持续性变化，导致各铰链等效刚度值也持续变化，故机构整体刚度呈现出一定的非线性，而这种特性有助于强化被动隔振性能[16]，在一定程度上能够拓宽平面柔性铰链的应用范围。

4 应用实例验证

为验证平面柔性铰链的应用可行性及隔振性能，在本研究中我们将其引入到图9所示的6DOF并联隔振平台中，替换原来的6个虎克铰，形成由上平台、球铰、带滑动副的支腿、平面柔性铰链、下平台组成的新隔振平台。

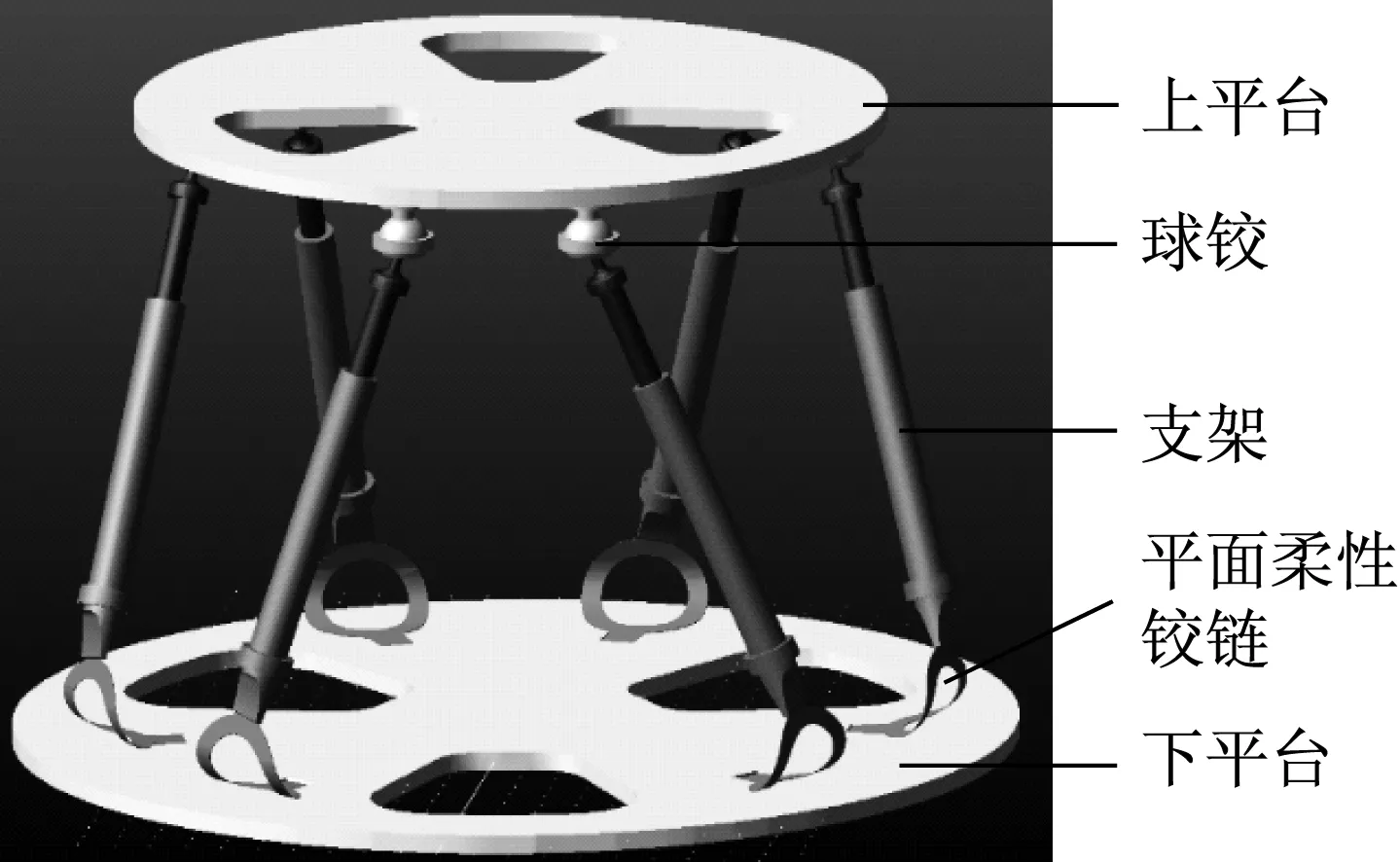
图9 引入柔性铰链的6DOF并联隔振平台

4.1 平面柔性铰链的应用验证

在下平台质心持续施加绕x轴转动激励RotX=3d*sin(PI*110*time)、绕y轴转动激励RotY=2d*sin(PI*110*time)以模拟振动输入，在ADAMS中对新隔振平台进行刚柔耦合动力学仿真分析。其中，平面柔性铰链是在ANSYS 15.0中划分网格后导入的mnf柔性体。下平台的输入由新隔振平台的被动隔振作用输出到上平台。定义上平台质心角加速度与下平台质心角加速度的比值为振动传递率η。取步长为0.01 s，仿真时间2 s。

得到的新隔振平台传递率变化如图10。平台的传递率呈周期性小幅度波动，基本稳定在0.1附近，最高不超过0.3。由传递率定义可知，当η<1时即具有隔振效果，故新平台能实现隔振功能要求，即该平面柔性铰链满足虎克铰的功能要求。

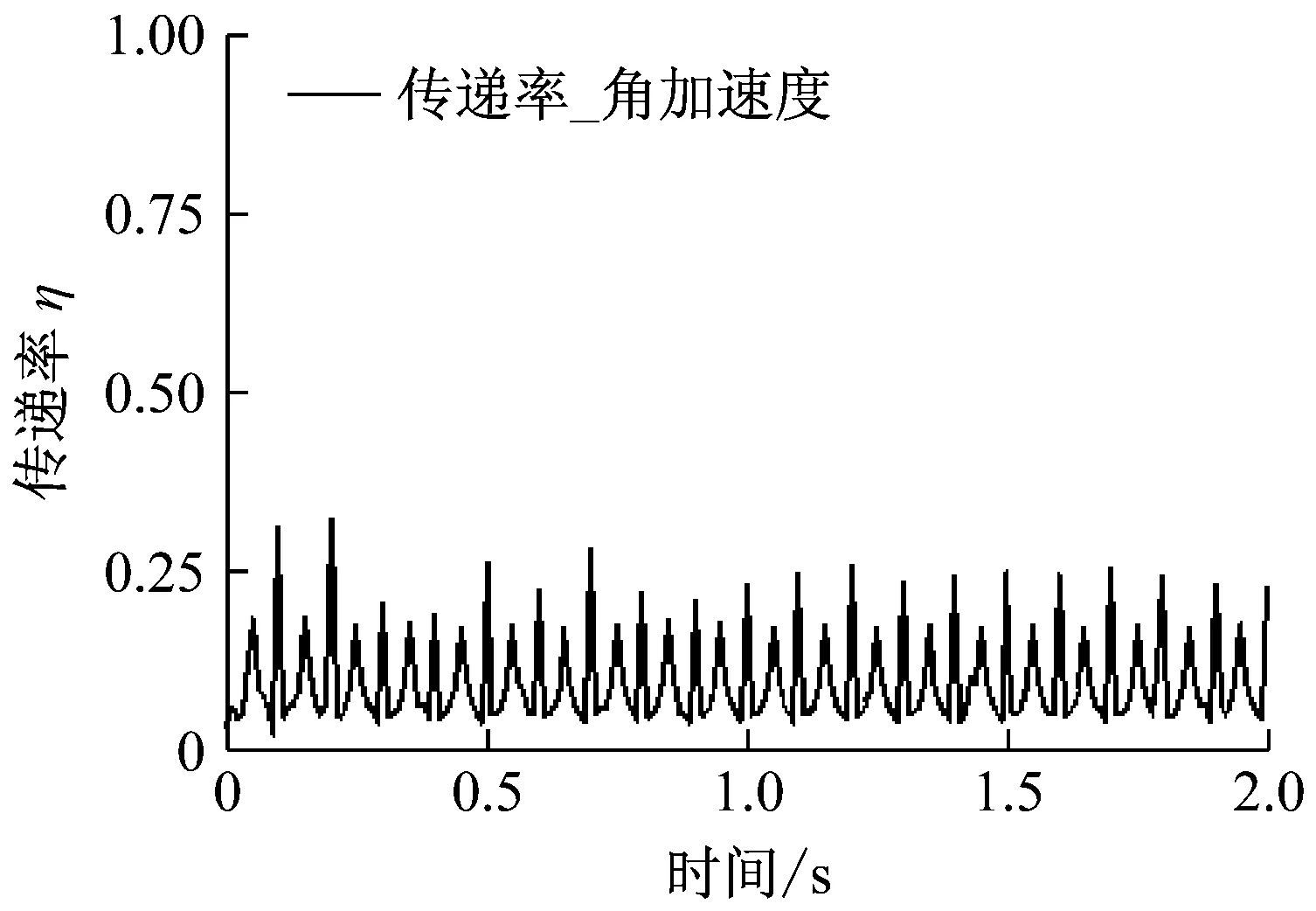
图10 采用平面柔性铰链的新隔振平台传递率

4.2 与含间隙虎克铰的隔振性能对比验证

对原隔振平台中6个虎克铰十字轴中的12个转动副添加0.02 mm径向间隙与0.06 mm轴向间隙，其他参数和施加的激励与4.1小节中一致，以对比分析两种铰链对运动传递的影响区别。从图11可以看出，加入间隙的原隔振平台的传递率η在1附近大幅度振荡，振荡频率较高，且有较多峰值已远大于1，丧失了隔振效果。即含间隙的虎克铰严重影响了运动传递的准确性。

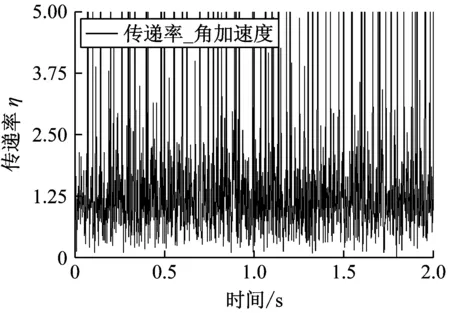
图11 采用含间隙虎克铰的原隔振平台传递率

对比结果表明：平面柔性铰链在满足虎克铰功能要求的同时能有效避免铰链间隙带来的影响，保证了运动的正确传递，实现较好的被动隔振效果。

5 结 论

刚性铰链的运动副间隙影响着机构的工作性能与寿命。而传统的柔性铰链多为单一转动副，对于多自由度柔性铰链一般存在着结构臃肿复杂的问题，为此，本研究提出一种适用于柔顺机构的等效虎克铰运动的平面柔性铰链，基于动态的等效刚度对铰链进行了理论建模和分析。得到的结论如下：

(1) 平面柔性铰链六个柔度值的对比表明：铰链的变形方式满足虎克铰的自由度要求，能极大地简化结构，为虎克铰提供了一体化的柔性方案，也为多自由度柔性铰链的设计提供了新的思路。

(2) 所建立的铰链动态等效刚度计算模型能正确地展现铰链刚度与姿态之间的关系。

(3) 不同参数铰链在大偏角下的刚度变化情况存在共性，根据所得规律拟合出非线性刚度的近似理论计算公式。

(4) 引入平面柔性铰链的6DOF并联平台工作性能优于含间隙的原平台，即：平面柔性铰链在满足虎克铰功能性要求的同时能有效避免虎克铰间隙引起的振动传递率突变问题。