基于混沌理论的音乐信号非线性特征研究
2019-02-21赵志成方力先
赵志成, 方力先
(杭州电子科技大学,杭州 310018)
音乐是反映人类现实生活情感的一门艺术,能够唤起情感上的共鸣。当听觉系统接受音乐刺激时,都会短时提高一部分特定神经细胞的兴奋性,影响到情绪表达[1]。这个过程必然会影响人体内分泌,促使人体产生一些激素或者酶。理论上,若能通过特定音乐刺激,促使人体产生一些有益的激素或者酶,则可达到加强新陈代谢,增强人体免疫力等对人体有益的效果。音乐的这种奇特功能是由音乐信号本身特征所决定的。
传统的音乐物理学基本上是从线性的角度去分析的,但真实的音乐系统一定是一个时滞的非线性动力系统[2]。非线性的来源有媒质中的黏滞性、非线性阻尼、热传导、弛豫现象和非局域性等等。而时滞系统往往具有多自由度、高维度特性,在系统的演化过程中,会伴随着弱混沌现象[3]的产生。因此,应用非线性的科学思想及方法对音乐信号进行研究,论证音乐信号的混沌机制,揭示音乐信号的本质规律并掌握信号的非线性特征[4],能够更好的帮助我们应用音乐信号治疗疾病,特别是神经系统疾病。
钢琴曲自产生以来一直被誉为最有逻辑,最能打动人心的高雅艺术之一,从某种意义上它最能反映人的情感变化。本文选择不同风格的钢琴曲以及Disco乐曲,经“分帧”、分析功率谱、计算Lyapunov指数、计算关联维数等步骤,从非线性的角度论证了音乐信号的特性,分析了不同风格类型音乐信号的非线性特征变化。
1 音乐信号的非线性特征分析
音乐信号是一类非稳态的非线性信号,混沌理论是分析非线性信号的有效方法,其中常用的分析方法有:分析Lyapunov指数[5]、分形理论[6]、熵理论[7]等。
1.1 分形维数
分形是非线性动力学系统的一个重要的分支,研究的对象具有自仿射性或者自相似性,反应了事物本身所固有的结构特征。按照分形理论,分形内部任何一个相对独立的部分,在一定程度上都是整体的再现与缩影。
分析时间序列常采用关联维数计算方法,它是在Token的“嵌入理论”以及Packard相空间重构理论基础上提出来的一种算法,又称为G.P算法[8]。算法的原理是在m维相空间内嵌入一个一维序列得到点集,序列的长度为n。用关联积分来表示吸引子中的点之间距离分布的概率,并求出关联维数的最佳估计。
相空间重构[9]:设嵌入序列的值为N,选取恰当的时间延迟τ,则相空间中的向量为:
Xi=[xi,xi+1,…,xi+(m-1)τ]2
(1)
式中:i=1,2,…,N,N=n-(m-1)τ,n为原时间序列;m为嵌入维数,通过上面的方法构造出N个m维矢量,当m≥2d+1时,吸引子的几个特征可以由这些矢量在相空间中的轨迹特征描述。
G.P.算法定义如下:取一维序列中的数据构成相空间中的m维向量将向量依次向后移动(取整数且为采样间隔),构成m维相空间中的另一个向量。以固定间隔向右依次移动便得到拓展而来的相空间中的点集{xi}i=1,2,…,N,其中N=n-(m-1)τ是点集中点的数量。
在相空间的点集中任取一点作为参考点,统计剩余点集中有多少点落在以该点为中心,以r为半径的圆中,由此而得到关联积分:
(2)
式中:H(·)为Heaviside单位函数。假设dmax是吸引子中的最大伸展量,当r≥dmax时有:
(3)
当N→∞时,C(m)≈1。关联积分表示吸引子中点与点之间距离的概率函数:
(4)
式中:D2(m,r)是与m及r有关的常数。对于相距距离很小的r1和r2有:
(5)
对上式两边同时取对数,有:
lnCm(r2)-lnCm(r1)=
(6)
当|r1-r2|很小时,有D2(m,r2)≈D2(m,r1)。所以,由上式得:
(7)
因此,计算关联积分饱和状态下曲线的线性段斜率,即可作为关联维数的近似值。
时间延迟的选择:根据文献经验,时间延迟τ=15左右时,可得到的关联维数最为清晰,且干扰误差小。为了验证这一观点,在采样频率为44 100 Hz的条件下,截取钢琴曲《For Elise》中的一小段音乐,利用平均位移法[10]进行实验。根据平均位移法的原理,在给定嵌入维数m=15,20,30的情况下,对时间延迟τ由小到大取值,重构相空间后计算每一个τ处的平均位移量S(τ)。
(8)
当S(τ)的增长率下降到初始值的40%时,该点对应的τ即为最优时间延迟。并且采用平均位移法可有效消除噪声的影响。如下图1所示。分析结果发现当时间延迟为15和16时S(τ)的增长率下降到初始值的40%附近,即时间延迟取值较为理想,所以后续实验计算均在时间延迟τ=15的条件下进行。
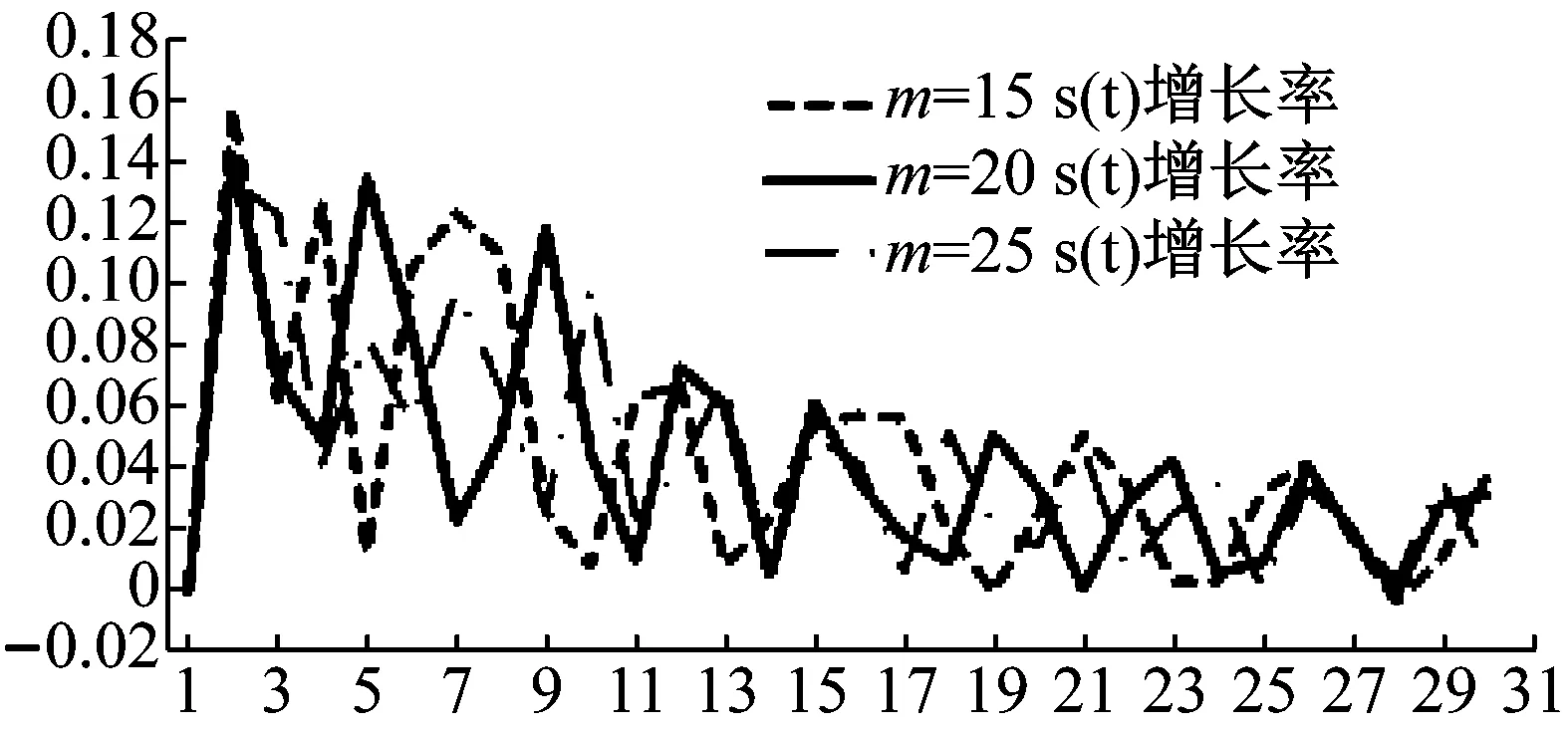
图1 平均位移量的增长率曲线
1.2 Lyapunov指数
Lyapunov指数是非线性动力学系统中一个重要的参数,代表了相空间中相邻轨道发散或者收敛的情况,是衡量系统非线性特征的一个重要指标。
对于一维离散映射:
xn+1=F(xn)
(9)
假设平均每次迭代所引起的指数分离中的指数为λ,于是原来相距为ε的两个起始点经过n次迭代后相距为
εenλ(x0)=Fn(x0+ε)-Fn(x0)
(10)
上式取对数求极限,可得:
(11)
称其为Lyapunov指数,代表了大量迭代的平均迭代分离指数。由上式可知,当λ>0时,相邻点运动呈分离趋势,对应于混沌运动;当λ<0时,相邻的点最终会合并成一点,对应于无混沌特征的线性运动。常用Wolf方法[11]计算Lyapunov指数。
2 实验与结果
2.1 实验材料
实验选择了已经通过凯泽窗类型的高通数字滤波器去噪的三首不同风格的钢琴曲与一首Disco乐曲作为主要的分析对象,具体如表1所示。

2.2 音乐信号的“分帧”
通常一首乐曲是一个复杂冗长的音乐信号,对其非线性重构后会是一个庞大的数据量,“分帧”是一个必然的选择。音乐家在作曲时会根据要表达的情感内容选择不同的节律为框架,再将代表了作者思想的乐符序列填入,也就有了曲谱上的小节划分。音乐家在谱写每一小节的乐曲时,必定带着整首曲子的思想,因此,每一小节都会是完整曲目信息片段的映射,不同帧的非线性特征构成了音乐信号的整体特征。所以,按照音乐的小节划分不会破坏整个音乐的非线性特征,通过帧的分析可以把握音乐信号的局部特征和整体特征,同时便于分析与计算[12]。
按照音乐曲式,我们将音乐信号按照曲式中的小节进行划分。如图2所示是致爱丽丝第一乐句中小节的划分,每两个箭头之间代表一个小节。

图2 《致爱丽丝》第一乐句中小节的划分
本次实验一共选择了三首不同风格的钢琴曲和一首Disco乐曲进行处理,对音乐信号的划分结果,如表2所示。
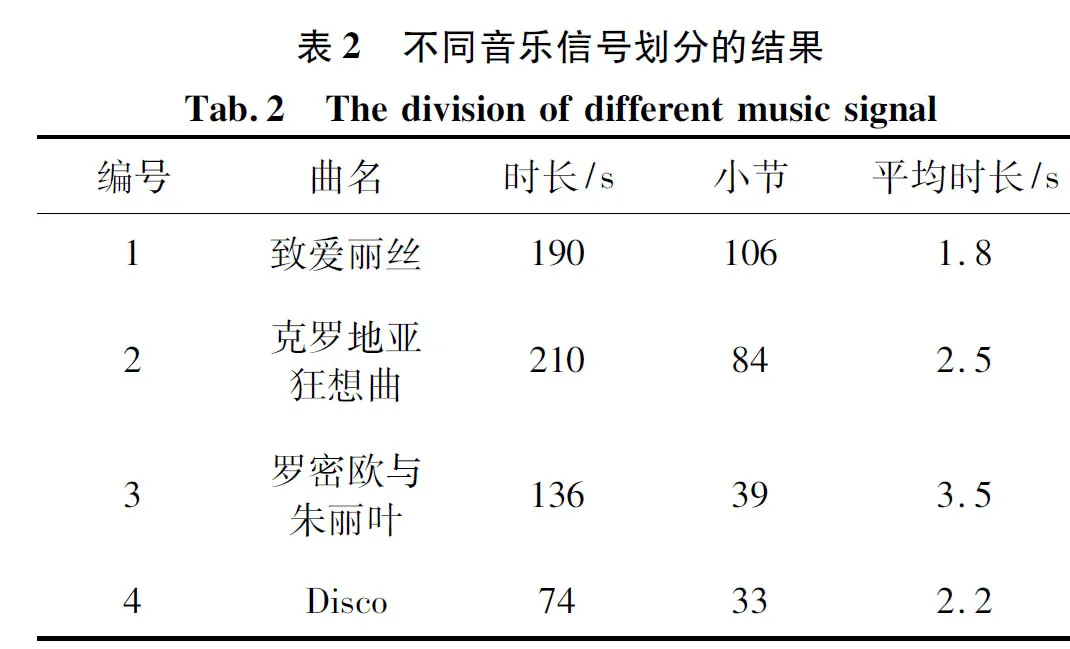
2.3 混沌特性的判断
功率谱分析[13]可以定性地分析音乐信号是否具有混沌特性。周期运动在功率谱中对应尖锋,混沌的特征是谱中出现“噪声背景”和宽锋。下面先通过功率谱图定性的验证了音乐信号具有混沌的特征。
图3是《致爱丽丝》某一片段的功率谱图,由图中我们可以看出,功率谱中的峰值连成了一片,存在一个宽峰,并在峰附近有明显的“噪声背景”,说明系统具有混沌的特征。各首音乐信号小节的功率谱图都有相似的特征。
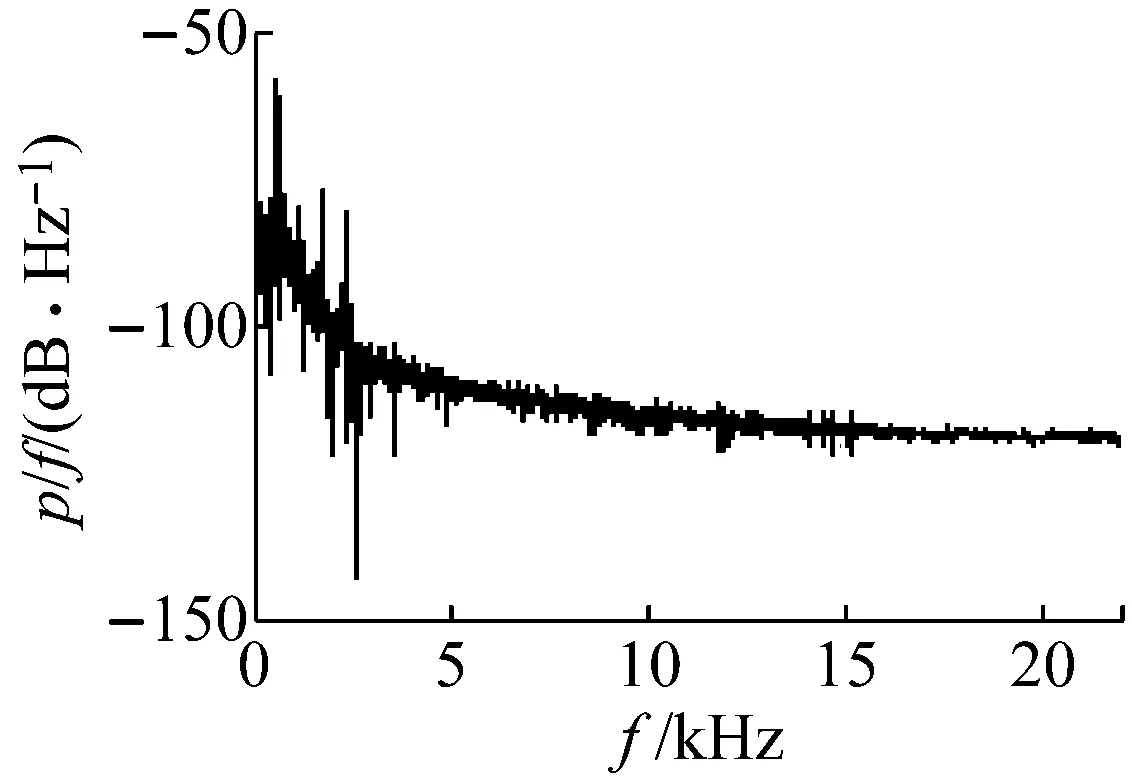
图3 《致爱丽丝》片段的功率谱图
Lyapunov指数是定量分析信号混沌特性的常用方法。图4是致爱丽丝音乐信号每小节Lyapunov指数的计算结果的折线图。
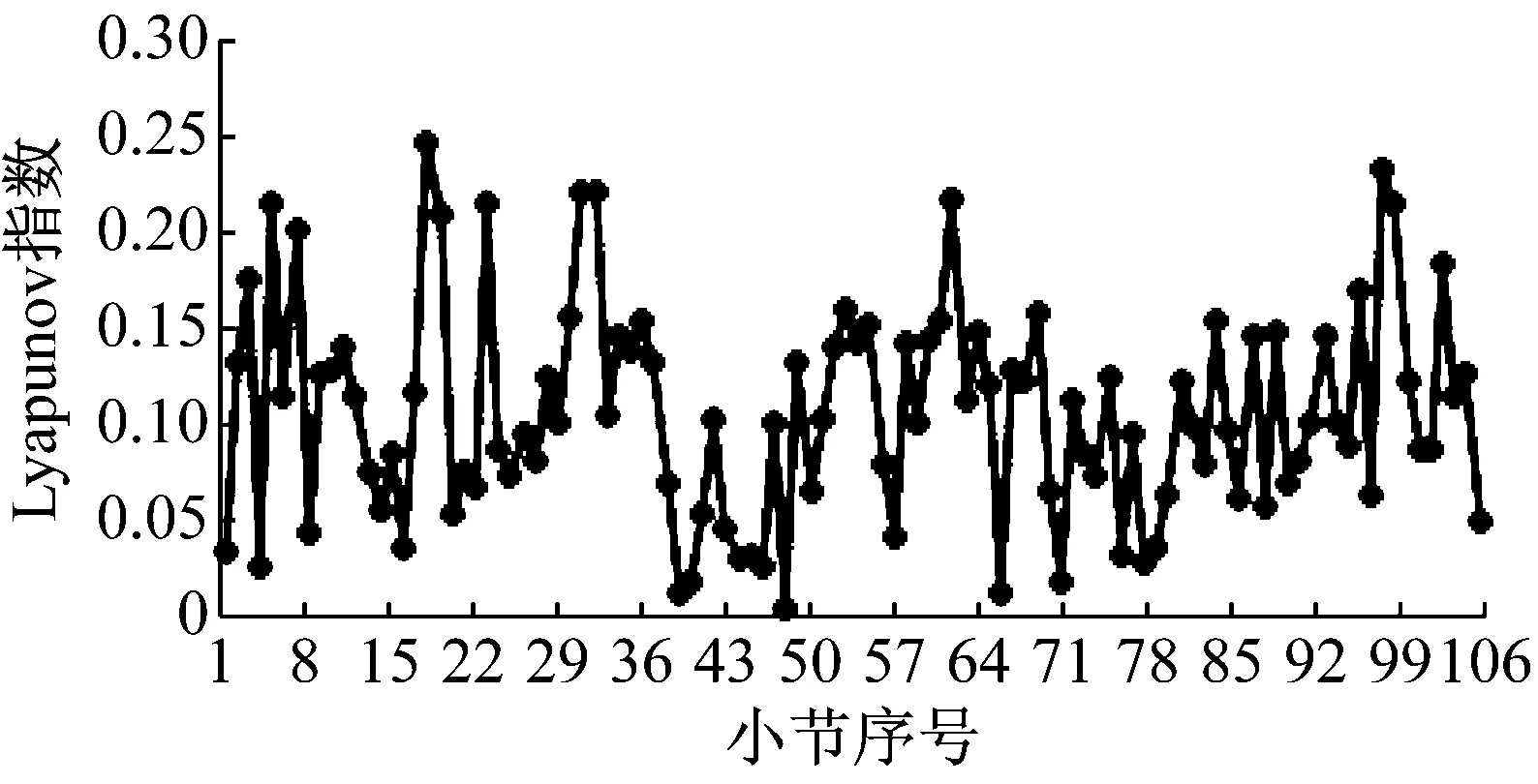
图4 《致爱丽丝》的Lyapunov折线图
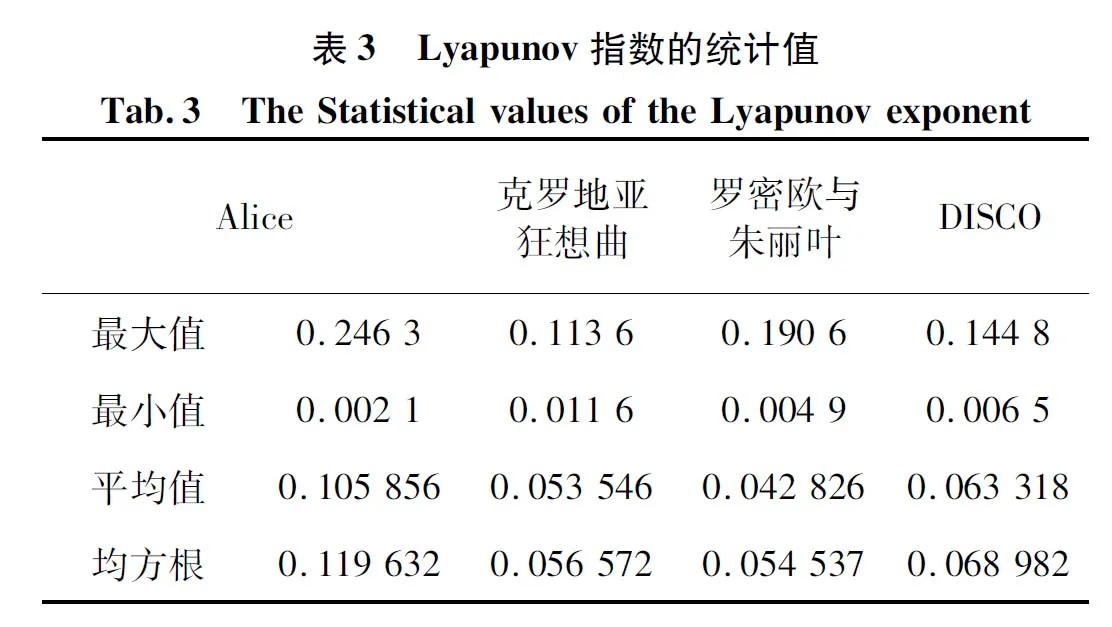
各首音乐Lyapunov指数的最大值、最小值、平均值以及均方根统计如下表3所示。
从Lyapunov指数的变化值以及相关统计值可以看出,音乐信号属于弱混沌信号,总体趋势是可控的,但是特定的音符在某个时刻发声的长短与强弱却是无法精确控制的,具有随机性。
2.4 关联维数的计算
计算关联维数利用G.P算法,选择时间延迟为15,缺省值为2,当曲线的斜率随着嵌入维数的增大而逐渐趋向于一个饱和值时,计算出此时饱和斜线的斜率,此时的值为关联维数的值。如下图5所示,当m=20时,直线趋于饱和,此时的斜率为16.240 7。
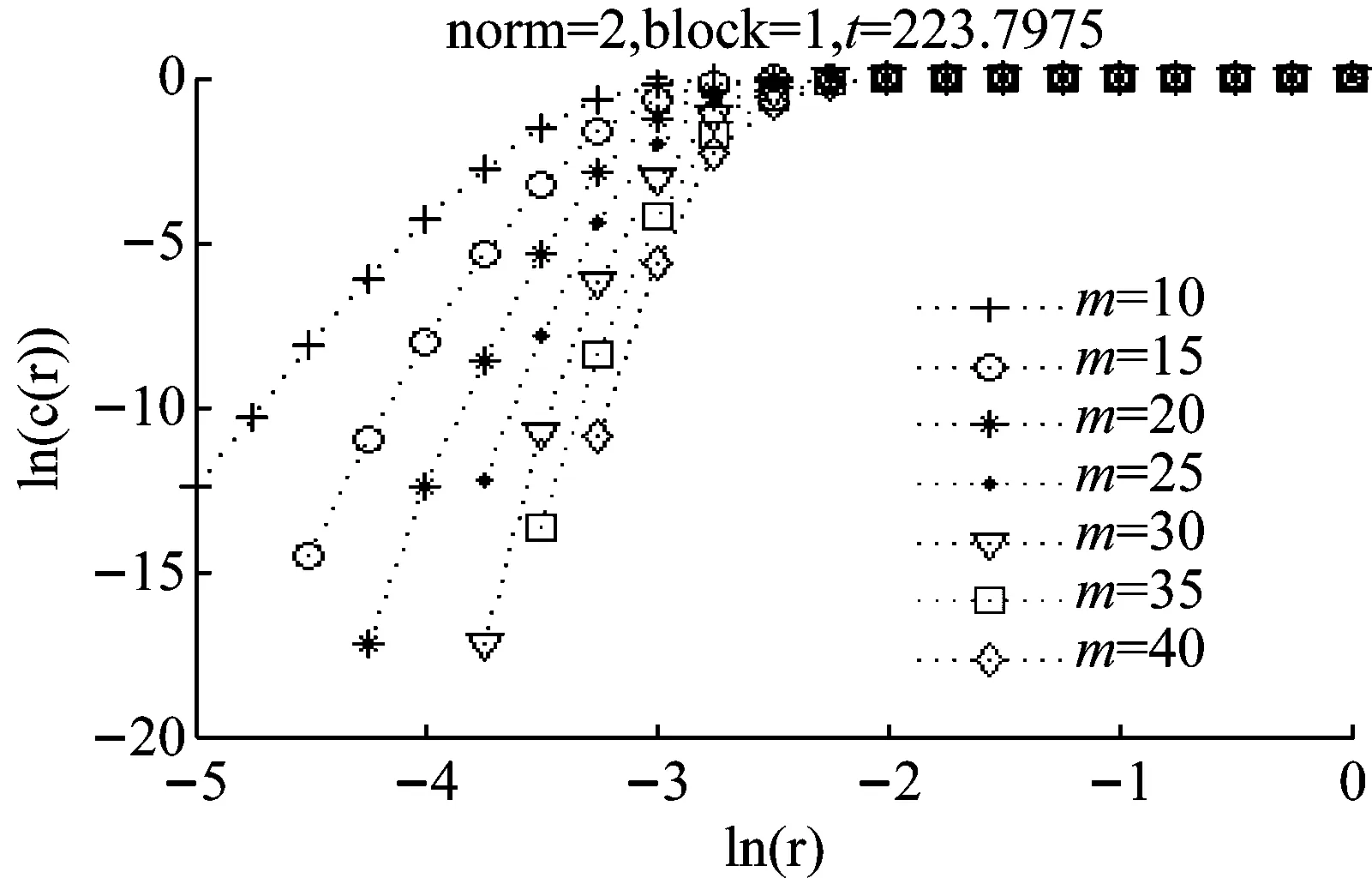
图5 《致爱丽丝》第30小节-关联维数图
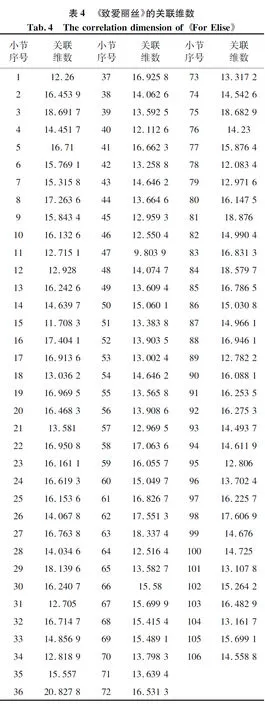
以此方法可计算出所有小节关联维数,并计录得表4。
以表4数据为基础可画得关联维数折线图,更直观的表现出各小节关联维数的变化趋势。如图6所示。

图6 致爱丽丝分节关联维数折线图
用同样方法获得DISCO音乐的各小节关联维数数据,并绘制关联维数折线图作为对照。如图7所示。
从以上关联维数折线图可分析得出,音乐信号是具有高维数的非线性信号,有复杂的周期运动特征,且维数的变化是有限的或具有随机性。除此之外,钢琴曲的整体维数要高于DISCO乐曲。
2.5 差分后关联维数的计算
差分是一个线性降维过程。对音乐信号进行差分处理后计算其关联维数,可分析讨论差分阶次对关联维数变化的影响。对不同乐曲进行多阶差分并求出平均关联维数可画得关联维数折线图,更直观的表现出各乐曲关联维数的变化趋势。如图8所示。
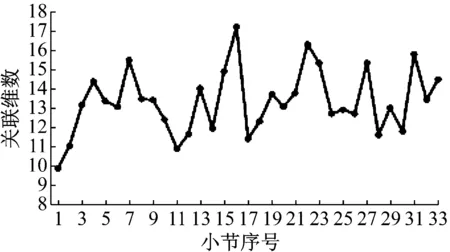
图7 DISCO音乐分节关联维数折线图
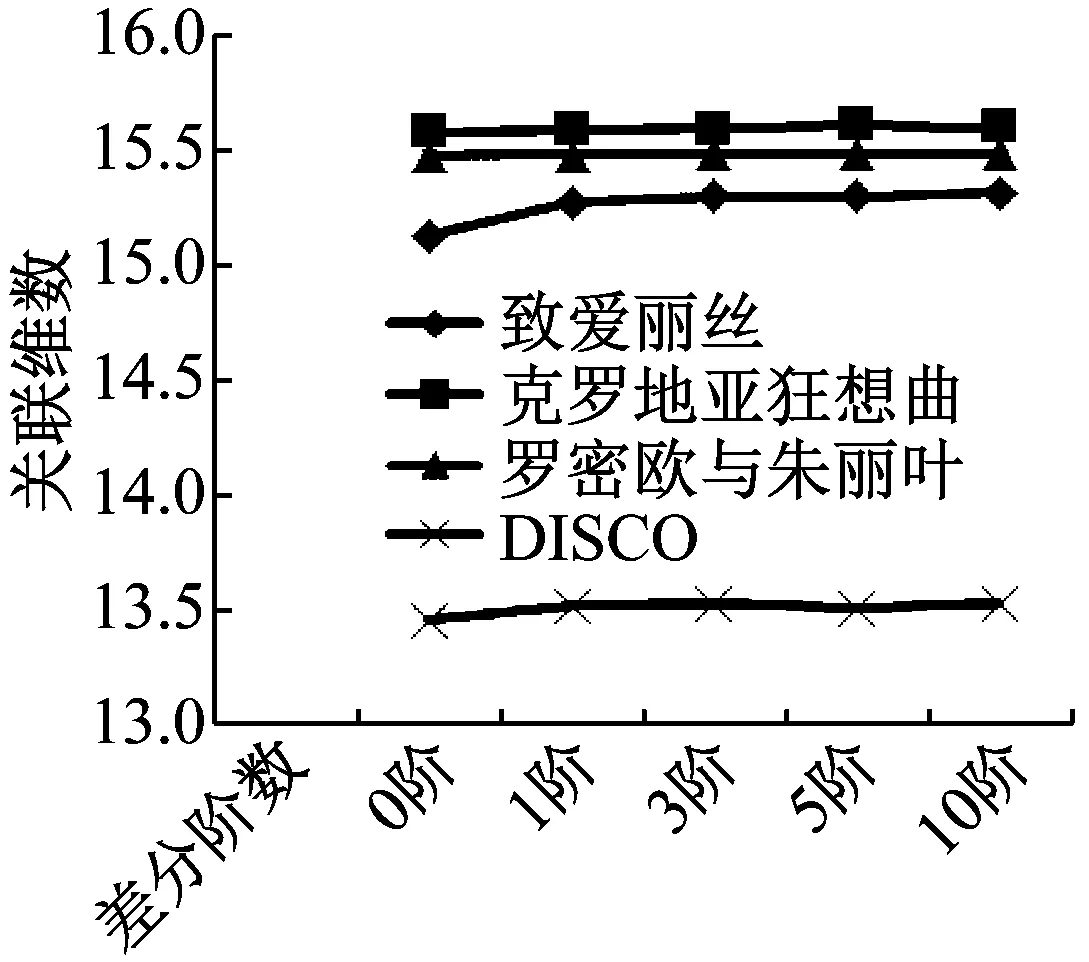
图8 差分后关联维数折线图
由图8可以看出,经过多阶差分以后,音乐信号的关联维数都在无差分时得到的值上小范围波动,考虑试验中的误差,我们可以认定,关联维数变化很小,音乐信号中的非线性特征具有稳定性。也可以看出钢琴曲的关联维数相对集中且远高于Disco音乐的关联维数,这意味着钢琴曲有更强的规律性。
3 结 论
根据计算分析三首钢琴曲以及一首Disco乐曲的功率谱、Lyapunov指数和关联维数等非线性特征量,可验证音乐信号据有如下特征:
(1) 弱混沌是音乐信号的非线性特征之一,这与音乐信号的可控性是符合的。事实上,音乐也是由人主观能控的弹奏各种乐器组合而成的。
(2) 准周期运动是音乐信号的主要特征。以经典钢琴曲为例,以小节为划分单位的维数变化具有随机性,但维数变化始终维持在一个有序可控的范围内,这体现了音乐信号是随机性与秩序性的统一。其中经典钢琴曲的维数明显高于其它音乐信号,表明经典钢琴曲的非线性特性更强,更容易在生理上被人接受。
(3) 音乐信号具有非常稳定的非线性特征。通过差分的方法对音乐信号进行线性降维后并未明显改变其平均关联维数,这体现了作曲时和声的稳定性原则。
传统思维上,功率谱、李雅普诺夫指数、关联维数等特征量只是针对自然界或工程界一般的信号分析量值。而将此方法引入到对乐曲这个人类高级思维活动的成果进行研究,只是一个初步的探索。实际上,对乐曲的特征描述显然远远不止这个范围,所得结论也是有局限性。
