复杂激励下复合行星传动系统频率耦合与耦合共振研究
2019-02-21窦作成李以农曾志鹏杜明刚
窦作成, 李以农, 曾志鹏, 杜明刚, 杨 阳
(1.重庆大学 机械传动国家重点实验室,重庆 400044;2.中国北方车辆研究所,北京 100072 )
复合行星变速传动系统具有高扭矩/质量比、高可靠性、高平稳性、高传动效率等优点,被广泛运用汽车和航空工业中[1-2]。行星传动系统在运行过程中,不仅受到外界载荷激励影响[3-4],同时受到时变刚度等内部激励的作用[5-6],从而对系统传动稳定造成较大影响[7-8]。而内外激励又会产生各种耦合振动,由此导致系统产生非固有频率共振,给系统参数设计带来更大的困难。针对行星传动的耦合振动问题,Inalpolat等[9]研究了行星齿轮制造误差对轮齿啮合力调制边频带的影响。王世宇[10]研究了啮频及其倍频激励对行星齿轮传动共振失效概率的影响。杨建明等[11]对各构件弹性化引起的三环减速器超谐振现象进行了分析。刘辉等[12]对两级简单行星传动系统的行星排级间的频率耦合进行了研究。目前对行星传动频率耦合的研究主要还集中在简单行星排和定值或单频驱动转矩,对内外复杂激励共同作用下复合行星系统的频率耦合研究还比较少。
本文以复合行星传动系统为研究对象,建立了考虑时变啮合刚度、啮合间隙、啮合误差等多种非线性因素的复合行星传动系统动力学模型,研究了发动机时变转矩输入、定值转矩输入等不同外界激励与多种内部非线性激励同时作用下对复合行星传动系统频率耦合的影响。并分析了内外激励引起的频率耦合产生的系统耦合共振问题,为系统设计时避开非固有频率的耦合共振和了解系统耦合共振特征提供参考。
1 系统动力学建模
本研究系统为车辆行星变速传动系统中一种典型复合行星传动系统,其结构简图如图1所示。该系统含有三个离合器C1、C2、C3,通过改变离合器的分离与结合实现多种速比的传动,受篇幅所限,本次仅研究采用C1结合C2、C3分离一种传动工况。该工况下,动力通过右侧内圈齿圈传入系统,然后通过输出轴输出到左右两端的负载,太阳轮始终处于空载状态。

图1 复合行星传动系统简图
1.1系统动力学模型
研究中对齿圈、太阳轮、行星架采用相对地面不动的固定坐标系,行星轮采用随着行星架转动的旋转坐标系。复合行星传动系统的扭转振动力学模型如图2所示,模型中每组行星轮的个数用N表示,则模型共含有2N+6个自由度,下标c、s、r1、r2、1pi、2pi分别表示行星架、太阳轮、内齿圈、外齿圈、第i个内圈行星轮、第i个外圈行星轮。kw1、kw2、cw1、cw2分别为行星架与左右侧负载连接主轴的扭转刚度和扭转阻尼,k1pis、c1pis、b1pis、e1pis分别表示内圈行星轮1pi与太阳轮s的啮合刚度、啮合阻尼、啮合间隙以及啮合误差,其余参数都以该方式命名,不再赘述。
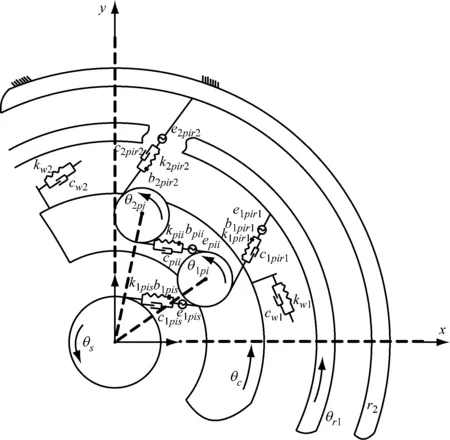
图2 复合行星传动系统扭振力学模型
Fig.2 Torsional vibration mechanical model of compound planetary transmission
为了便于系统方程的统一建立与求解,建模时将模型中的角位移通过式(1)转换为线位移。
ul=rlθl,l=c,r1,s,1pi,2pi
(1)
式中:rl分别为太阳轮s中心与内圈行星轮1pi中心的距离、内齿圈r1基圆半径、太阳轮s基圆半径、第i个内圈行星轮1pi基圆半径、第i个外圈行星轮2pi基圆半径,(l=c,r1,s,1pi,2pi)。
在系统动力学分析建模中,各构件运动方向均以图2中箭头标注方向为正,啮合弹性变形以引起啮合线压缩时为正,拉伸为负,同时认为齿轮啮合误差造成的弹性变形一直处于啮合线上,各轮齿间的啮合弹性变形量为式(2)所示。
(2)
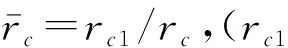
根据系统弹性变形的能量关系建立第二类拉格朗日方程,可求出系统动力学微分方程
(3)
(4)
式中:Tr1、Ts、Tc、T1pi、T2pi、Tw1、Tw2均为外界激励。
方程组式(3)可整理为矩阵形式:
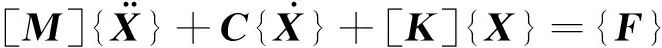
(5)
式中:M为系统等效质量矩阵,C为系统阻尼矩阵,K为系统刚度矩阵,X为系统广义坐标线位移阵列,F为外载荷列阵。
1.2 系统内外激励
研究中外部激励考虑发动机转矩波动变化引起输入系统转矩的变化,内部激励则考虑啮合时变刚度、齿形误差、啮合间隙及啮合相位等非线性因素对系统的激励。
选用Maatar等[13]所推导的公式对时变啮合刚度按啮合频率进行傅里叶展开
(6)
An=sin(2πnε)/(πnε)
(7)
Bn=(1-cos(2πnε))/(πnε)
(8)
式中:τ=t/Tm,t为时间;Tm为啮合周期;b为齿宽;ε为直齿圆柱齿轮副的重合度;k0为静载荷下单位齿宽单齿啮合刚度;n为傅里叶级数的项数。
轮齿啮合频率及啮合周期:
(9)
(10)
式中:zr1,zr2分别为内外齿圈齿数;ωr1为齿圈r1转速;ωm为复合行星传动系统轮齿啮合频率。
在对复合行星传动系统进行建模时,考虑偏心误差和齿形误差作为系统综合误差。假定行星架的安装和制造偏心误差都包含在了太阳轮和齿圈误差中,因此分析中仅考虑齿轮的偏心误差。
太阳轮、齿圈、行星轮间的轮齿啮合误差用齿轮啮频为激励频率的正弦函数表示
(11)
式中:ex1pir1为内齿圈r1和第i个内圈行星轮1pi的齿形误差;ex2pir2为外齿圈r2与第i个外圈行星轮2pi的齿形误差;ex1pis为太阳轮s与第i个内圈行星轮1pi的齿形误差;expii为第i个内圈行星轮1pi与第i个外圈行星轮2pi的齿形误差;A1pir1、A2pir2、A1pis、Apii分别表示与其对应的误差幅值,β1pir1、β2pir2、β1pis、βpii分别表示与其对应的齿形误差初相位。
太阳轮、齿圈、行星轮的偏心误差均可用各自相对转频的正弦函数表示,将内外齿圈、太阳轮、行星轮的偏心误差投影到齿轮啮合线方向,可得出
(12)
式中:Φ=ωzct+ηz-2π(i-1)/N;Θ=ωzct+ηz;Ex1pir1为内齿圈r1和第i个内圈行星轮1pi的偏心误差在其啮合线上的分量;Ex2pir2表示外齿圈r2与第i个外圈行星轮2pi的偏心误差在其啮合线上的分量;Ex1pis表示太阳轮s与第i个内圈行星轮1pi的偏心误差在其啮合线上的分量;Expii为第i个内圈行星轮1pi与第i个外圈行星轮2pi的偏心误差在其啮合线上的分量;Es、Er1、Er2、E1pi、E2pi分别表示太阳轮s、内齿圈r1、外齿圈r2、内圈行星轮1pi、外圈行星轮2pi的偏心误差,ωzc分别表示与其对应的各齿轮相对于行星架的转速,ηz分别表示与其对应的偏心误差初相位,(z=r1,r2,1pi,2pi)。
则复合行星齿轮传动系统的偏心误差及齿形误差激励在啮合线上的等效位移可表示为
eΔ=exΔ+ExΔ,Δ=1pir1,2pir2,1pis,pii
(13)
齿侧间隙通常可用如图3所示的一个分段函数表示,啮合间隙函数f(δ)的表达式为

(14)
式中:b为单边齿侧间隙;δ为齿轮啮合的相对扭转位移。

图3 非线性齿侧间隙函数
复合行星传动系统的外界驱动激励主要来自于发动机,系统输入驱动激励源于V型8缸四冲程柴油发动机,其转速为1 000 r/min、2 500 r/min时的扭矩输出分别如图4(a)、(b)所示。

(a) 转速为1 000 r/min时发动机输出扭矩
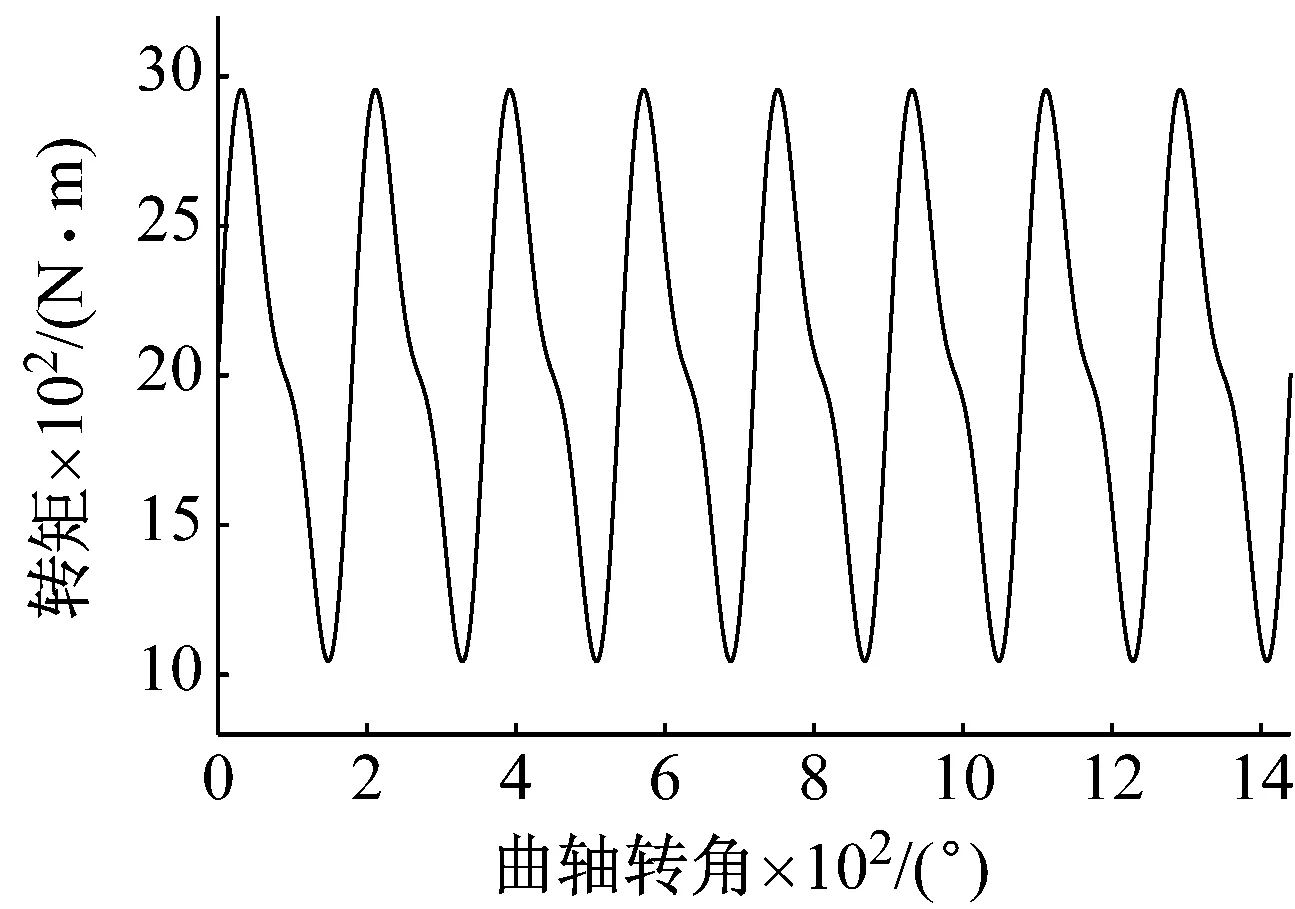
(b) 转速为2 500 r/min时发动机输出扭矩
2 内外激励频率耦合分析
2.1 耦合机理
行星传动系统在运行中受到发动机、负载等外界载荷激励,还受到时变啮合刚度、啮合误差、啮合间隙等多种内部激励的影响,研究内外激励对系统振动的耦合影响可以更好地分析系统振动产生的原因和特点。本文通过分析内齿圈r1与内圈行星轮1pi的啮合力来研究内外激励下系统振动的耦合机理,研究内外激励对产生系统耦合振动的原因和特点。啮合变形量可展开成以各内外影响因素各自激励频率为基频的Fourier级数之和,轮齿的啮合刚度也分解为Fourier级数之和,则系统啮合力F1pir1可表示为
(15)
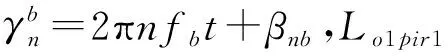
F1(t)~F5(t) 这五类含不同频率成分的弹性啮合力是啮合力中波动部分的主要成分,是引起系统振动的原因,对各弹性啮合力进行相应的时频变换可得F1pir1在频域中的表示
(16)

由此可得系统的调制频率为
f=Mfm+Nr1fr1+Nefe+Nr2fr2+Nsfs
(17)
从F1pir1(f)可以看出,啮合力因时变啮合刚度、各种啮合误差、外界激励发生周期性波动而出现调制现象,在频谱上会产生一系列以啮合频率及其倍频为载波频率,以各部件相对行星架转频及其倍频、外界激励频率及其倍频为调制频率的边频带。
2.2 频率耦合数值分析
复合行星传动系统计算采用的相关参数如表1所示,取系统在转速为1 000 r/min、2 500 r/min时,恒定驱动力矩为700 N·m、2 000 N·m以及发动机时变转矩激励作用下,对系统的内齿圈r1与内圈行星轮1p1的啮合力及主轴左端轴段剪切力频谱分布规律进行分析。系统分别在恒定驱动力矩2 000 N·m、700 N·m作用下转速为2 500 r/min与1 000 r/min的频谱图如图5、图6所示。
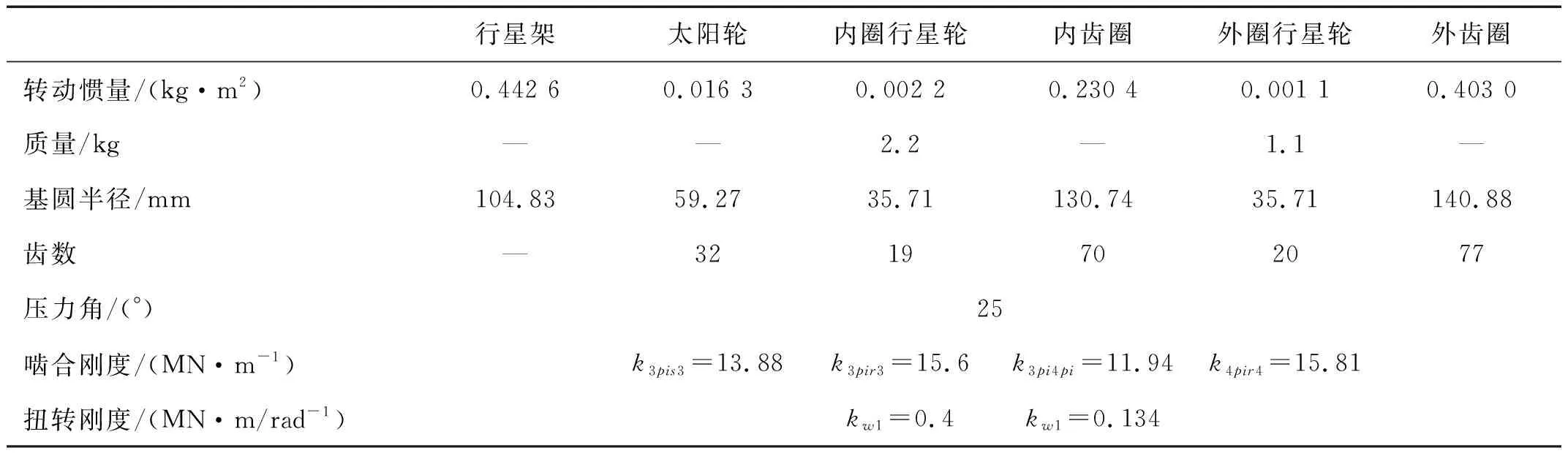
表1 复合行星传动系统相关参数
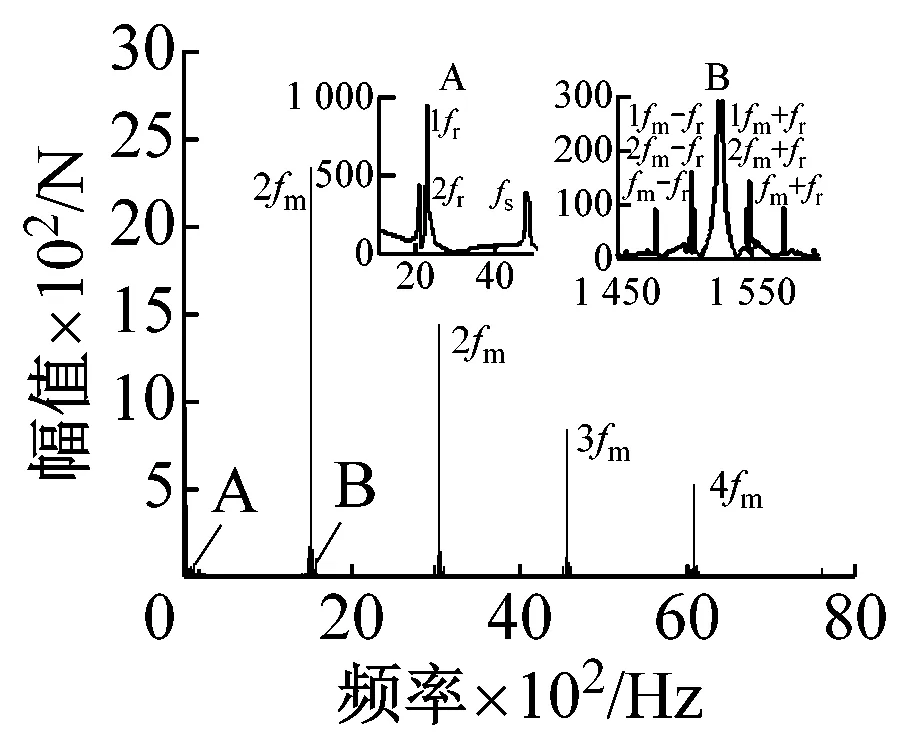
(a) n=2 500 r/min啮合力

(b) n=2 500 r/min轴段剪切力

(d) n=1 000 r/min轴段剪切力

(a) n=2 500 r/min啮合力
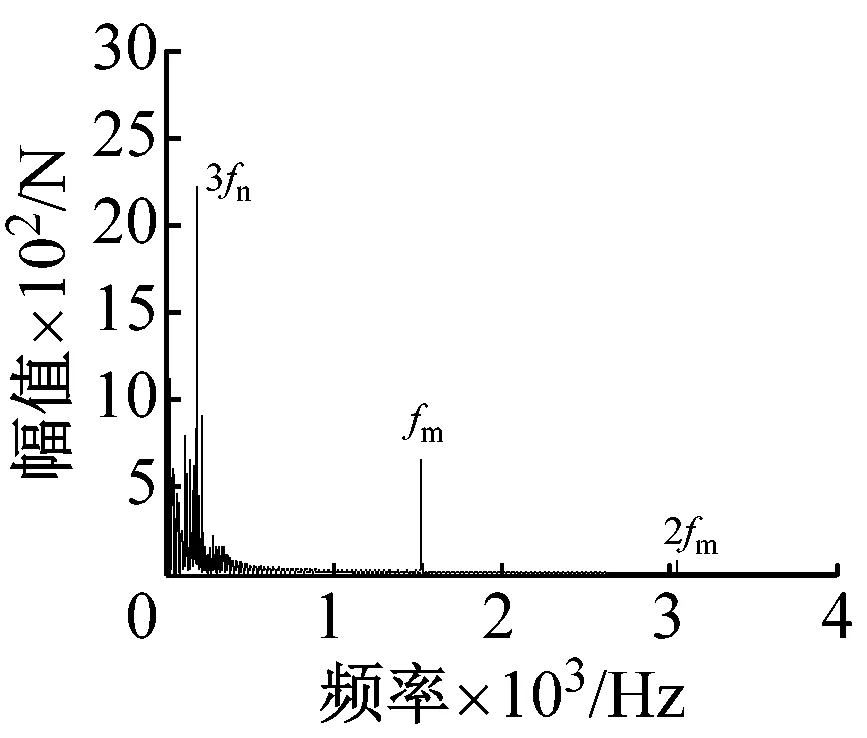
(b) n=2 500 r/min轴段剪切力

(c) n=1 000 r/min啮合力

(d) n=1 000 r/min轴段剪切力
从图5(a)、(c)与图6(a)、(c)中可以看出,轮齿啮合力所含的主要频率成分中有啮频及其倍频,内齿圈的相对转频fr1、太阳轮的相对转频fs、以啮频为基频各相对转频为调制频的频谱,如fm±fr1、fm±fr2、fm±fs。轮齿的啮频及其倍频1fm~4fm幅值较大,各中心旋转构件相对于行星架的转频以及其与啮频的调制频率幅值较小。由于系统轮齿含有时变啮合刚度及啮合间隙等非线性因素,因此系统中也出现特殊频率成分,如图6(a)A中出现2倍太阳轮相对转频2fs以及1~3阶派生固有频率。由fm的幅值分析可得,系统定值驱动力矩越大,啮频激励引起的响应幅值越大。而定值驱动力矩一定时,转速变化对啮频激励引起的响应幅值影响较小。图5(b)、(d)与图6(b)、(d)中由于复合行星传动系统中的时变刚度及冲击等非线性因素,系统主轴轴段剪切力的频谱图中也出现了前几阶派生固有频率。频谱幅值较大的为第三阶派生固有频率fn3、太阳轮相对转频fs、系统轮啮频fm。同时还可以看出,系统低转速时啮频对主轴的影响较高速时更大。
图7、图8分别为约束转矩为2 000 N·m、700 N·m时,考虑发动机时变转矩激励,不同转速对应的系统轮齿啮合力及轴段剪切力频谱。从图7(a)、(c)与图8(a)、(c)中可以看出,在不同转速和激励下,啮频及其倍频、发动机激励频率及其倍频引起的轮齿啮合力幅值都较大。除此之外还存在各中心旋转构件相对于行星架的转频,以及以啮频及其倍频为基频与各中心旋转构件相对转频、发动机激励频率之间的调制频率,但其值较小。从图7(b)、(d)与图8(b)、(d)中可以看出,发动机激励的引入对主轴剪切力影响较大。轴段剪切力频谱中频谱幅值较大的为发动机基频及其倍频fe、2fe、太阳轮相对转频fs、轮齿啮合频率fm。由于系统非线性因素的影响,系统的局部也出现了某些特殊频率,如系统2、3阶派生固有频率等。
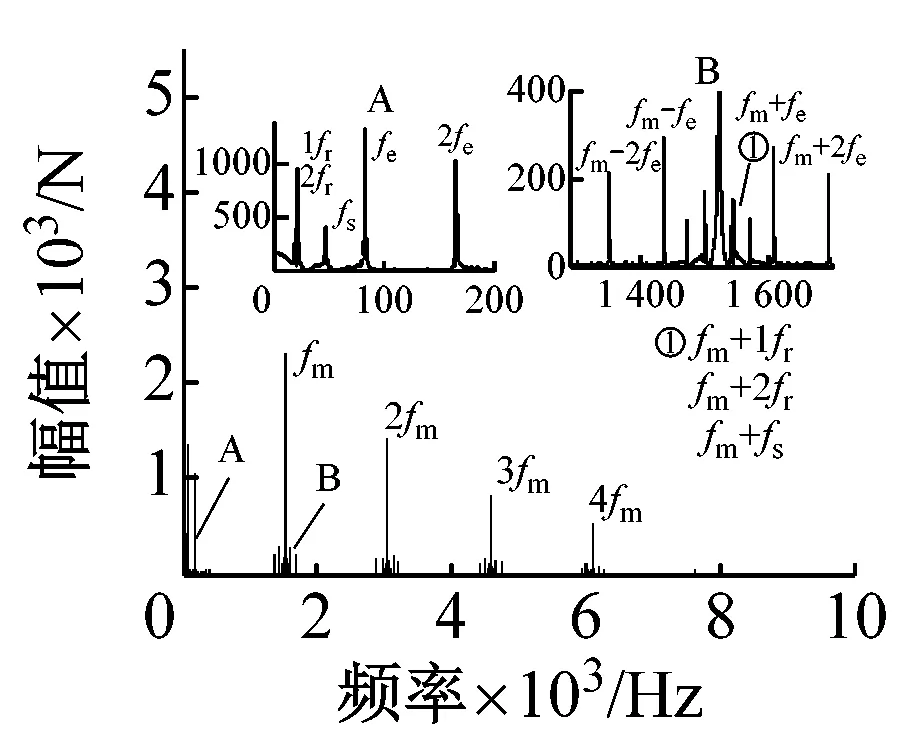
(a) n=2 500 r/min啮合力

(b) n=2 500 r/min轴段剪切力

(c) n=1 000 r/min啮合力

(d) n=1 000 r/min轴段剪切力
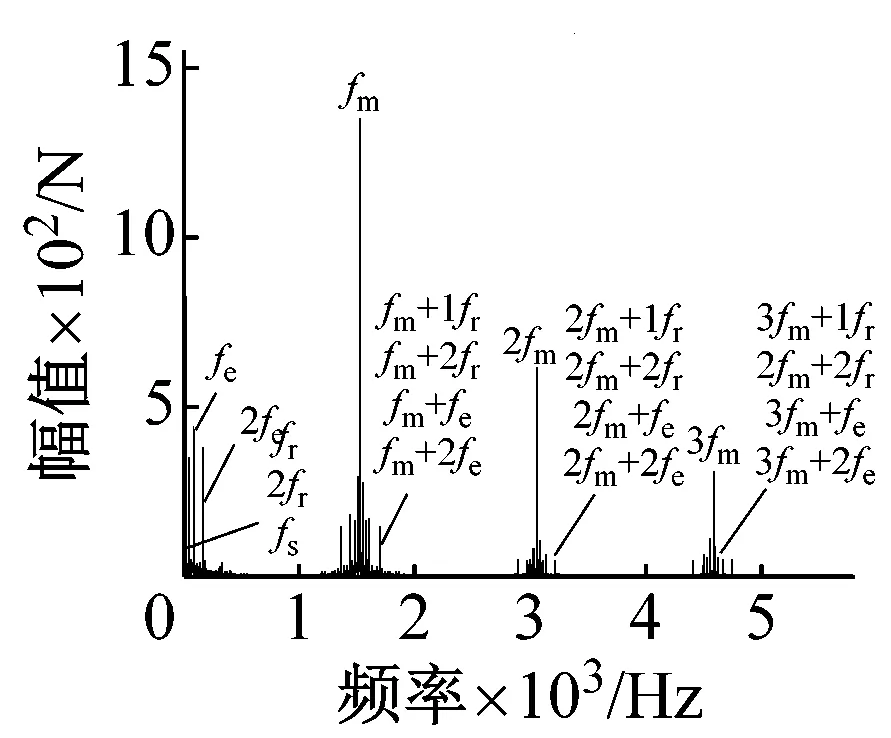
(a) n=2 500 r/min啮合力
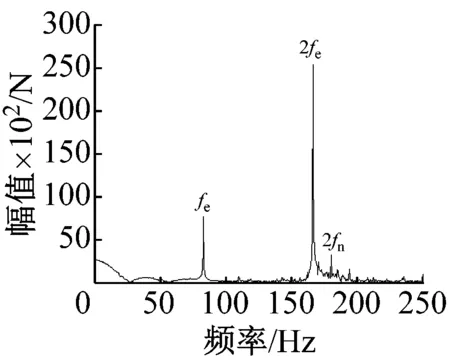
(b) n=2 500 r/min轴段剪切力
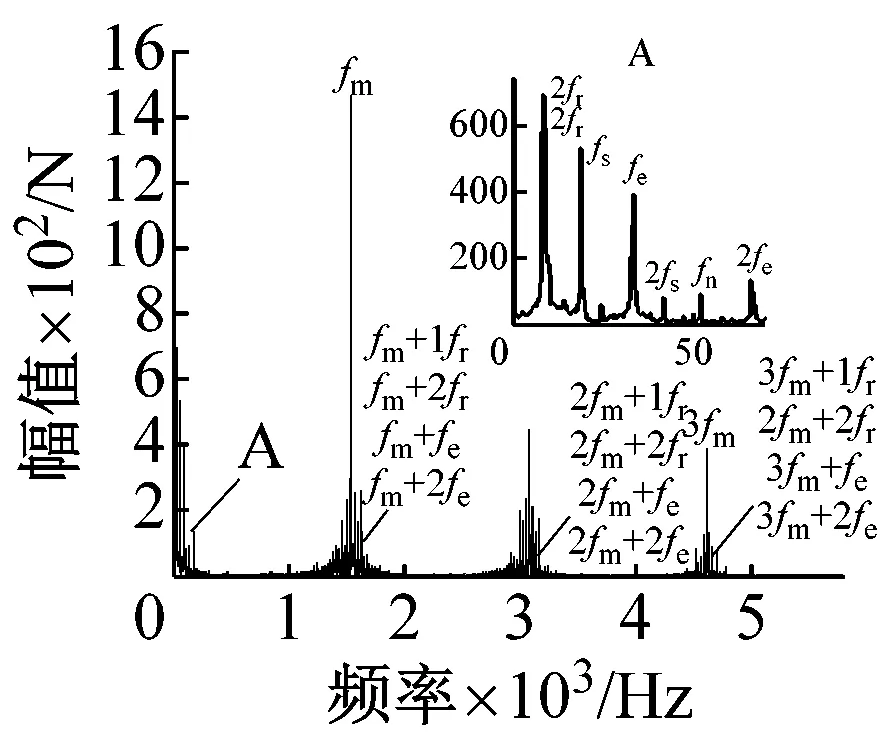
(c) n=1 000 r/min啮合力
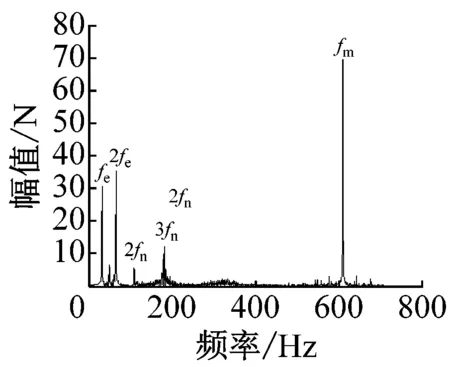
(d) n=1 000 r/min轴段剪切力
通过以上对系统不同转速及转矩条件下的啮合力及轴段剪切力的频域分析可以看出,当系统的驱动力矩为定值时,轮齿啮合力的主要频率成分为轮齿啮合频率及其倍频,主轴扭转剪切力的主要频率成分为轮齿啮合频率及派生频率。当系统的驱动力矩为时变转矩时,系统轮齿啮合力及轴段剪切力的频率成分引入了发动机激励频率,轮齿啮合力的主要频率成分为发动机转频及其倍频、轮齿啮合频率及其倍频、轮齿啮合频率为基频发动机转频为调制频的耦合频率。主轴扭转剪切力的主要频率成分为发动机转频及其倍频、轮齿啮合频率,且低速时啮率激励影响占优,高速时发动机激励影响占优。
当系统处于定值驱动时,系统中轮齿啮合力主要受时变啮合刚度等因素的影响,且一阶啮合频率的影响最大,然后影响程度依次递减,而齿轮的偏心误差及啮合误差对啮合力有一定的影响但不明显。主轴剪切力主要受系统时变啮合刚度的影响,当系统转速较低时时变啮合刚度的影响较为明显,随着转速的增加,系统时变刚度的影响逐渐弱化。当系统受到时变转矩激励时,系统中啮合力主要受发动机激励、时变啮合刚度的影响以及其相互耦合的影响,且各转速下时变啮合刚度的影响较发动机激励更为明显。主轴扭转剪切力主要受发动机激励及时变啮合刚度的影响,低转速下主轴扭转剪切力受时变啮合刚度影响更为明显,高转速下受发动机激励影响更为明显。
3 系统耦合共振分析
通常情况下线性系统的受迫振动共振转速只考虑系统固有频率及外界激励,但非线性系统受迫振动中,不仅含有外部时变激励,还包含众多内部激励,如轮齿间非线性系统中,啮合误差激励、时变啮合刚度激励以及啮合频率与外界激励频率调制产生的新激励频率,可能会出现主共振、超谐共振、亚谐共振、内共振等。因此仅考虑线性固有频率引起的振动必然会丢失掉某些重要激励频率导致的共振,而考虑系统内部及外部因素共同形成的耦合共振,可以更加全面分析系统振动特性。
非线性系统耦合共振主要考虑内部激励、外部激励以及内外部耦合激励三大类激励,这里主要是指轮齿啮合频率及其倍频、各相对转频及其倍频、外界激励频率及其倍频、啮合频率各阶谐频和外界激励各阶谐频调制产生的耦合频率等。系统的固有频率均可表示为平行于转速坐标轴的直线,而激励频率均可以表示为系统转速的函数,呈一系列通过转速原点的辐射状直线,当这些激励频率与固有频率相等时,系统就有可能发生共振,且该激励频率所对应的转速即为共振转速,它们的计算表达式为
(18)
定值转矩及时变转矩作用时,系统共振转速分析如图9所示,恒定转矩时系统啮合频率考虑了前3阶1fm~3fm,发动机时变啮合转矩为前两阶1fe~2fe,其内部激励与外部激励的调制频率fm±fe、2fm±fe、3fm±fe、fm±2fe、2fm±2fe、3fm±2fe。从图中可以看出,当系统仅含有内部激励时,系统共振转速仅为点状分布,当系统含有外界激励时,系统中出现了由于调制频率作用引起的较为密集的共振转速带如图9(b)中G1~G5、F1~F5、E6~E10等。且系统在恒定转矩作用下的共振转速均落于内外界激励调制频率导致的共振转速带中。系统的共振转速分布如表2所示,共振点1是由于发动机激励频率及其倍频所对应的共振转速,共振点2为系统啮合频率及其倍频所对应的共振转速,共振带是由于啮合频率及其倍频与发动机激励频率调制所产生的共振转速带。可以看出系统中由啮合频率及其耦合频率引起的共振转速带主要集中于1 200 r/min以下,而发动机激励频率导致的共振转速主要集中于1 200 r/min以上。

(a) 定值驱动转矩
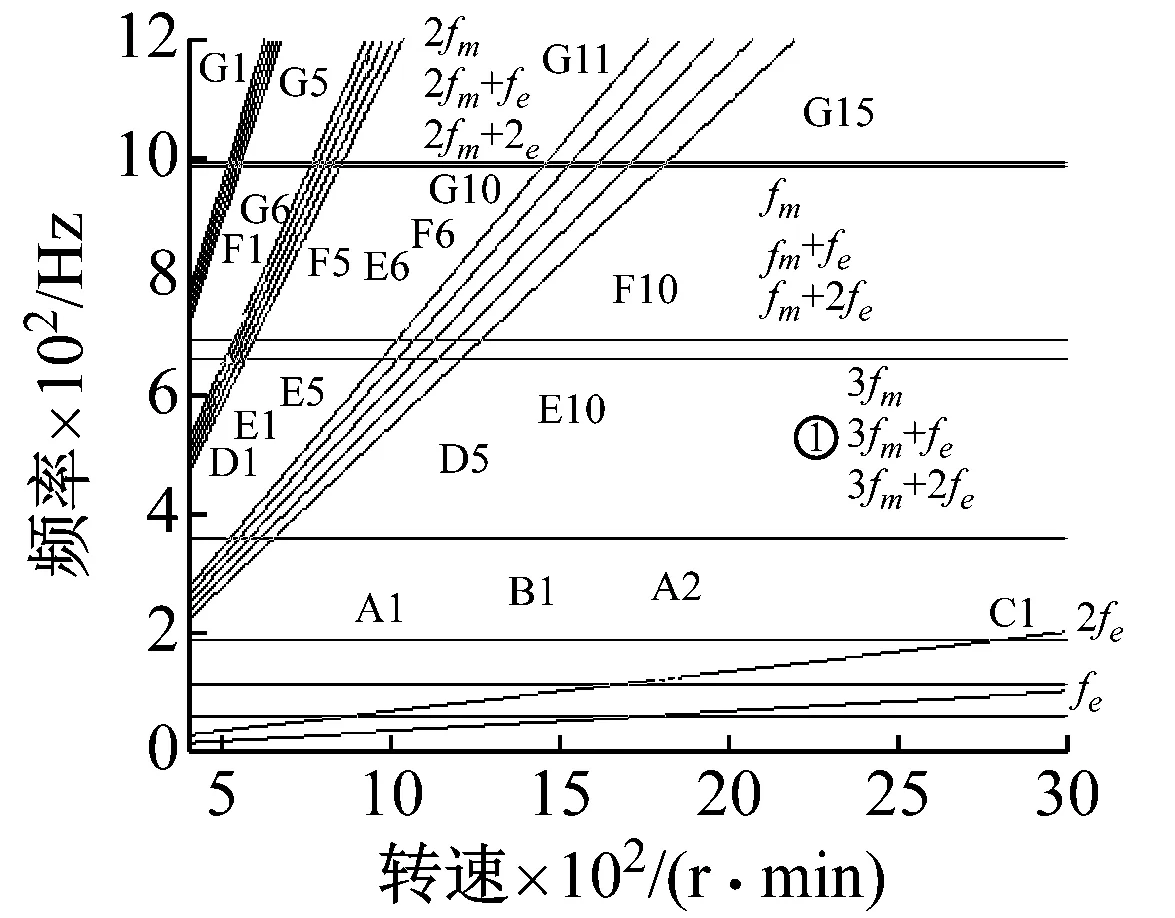
(b) 时变驱动转矩
表2系统耦合共振转速
Tab.2Systemcouplingresonancespeed

4 结 论
本文考虑定值、时变等多种不同外界激励与时变啮合刚度等多种非线性内部激励,以内齿圈和内圈行星轮啮合力、主轴扭转剪切力为例研究了复合行星传动系统在内外激励共同作用时产生的耦合振动特性,并分析了在内外激励下系统在工作转速范围内的耦合共振问题,得到了以下结论:
(1) 在定值转矩驱动时,齿轮啮合力与主轴剪切力的主要频率成分都为啮合频率及其倍频,系统定值驱动力矩越大,啮频激励引起的响应幅值越大,但转速变化对啮频激励引起的响应幅值影响不大。
(2) 在时变转矩驱动时,齿轮啮合力和剪辑力在各转速下的主要频率成分都为啮合相关频率,但主轴剪切力响应中啮合频率激励的影响随着转速的增大而逐渐减小,发动机激励的影响却呈相反规律。
(3) 复合行星传动系统共振转速带中,由啮合频率及其耦合频率引起的共振转速主要集中于1 200 r/min以下,而发动机激励引起的共振转速主要集中于1 200 r/min以上。
