基于演化博弈的建筑业绿色供应链激励优化策略研究
2019-02-21王磊高申征李玲玉
王磊,高申征,李玲玉
(天津城建大学经济与管理学院,天津300384)
近年来,随着城镇化的高速发展,我国建筑业能源、资源消耗及环境污染问题日益严重。为应对此问题,我国大力发展绿色建筑,但截至2016年9月,大多数的绿色建筑都停留在前期设计阶段,在后期运营维护阶段能够达到绿色建筑要求的建筑产品仅占绿色建筑的6%。绿色供应链管理正是实现建筑业节能减排的基础,是解决绿色建筑重设计轻运营等问题的重要方式,符合我国社会发展绿色经济的基本思路。而推动绿色供应链的发展离不开政府对其施加一定水平的激励。如何使激励政策发挥的效果最明显、通过有效措施和制度设计推动建筑业绿色供应链的发展是文中的研究要点。
为了提高绿色供应链的激励效果,国内外众多学者就建筑业绿色供应链进行了研究。其中第一类利用经济学理论论述了建筑业绿色供应链的特点,针对特点提出激励建议[1-4]。第二类主要利用动态博弈模型分析各利益方不同的利益动机及博弈行为,提出了符合博弈主体经济利益要求的建筑业绿色供应链构建途径[5-9]。第三类是基于系统动力学原理对建筑绿色供应链的经济、节能和减排系统进行建模、仿真实验与政策分析,从而提出促进建筑业绿色供应链发展的政策建议[10-11]。现阶段,针对建筑业绿色供应链的相关研究较少,且主要集中在建筑业绿色供应链管理理论、体系构建、运作体制以及绿色供应链相关参与者的行为研究。结合现阶段建筑业绿色供应链的应用实践来看,建筑业绿色供应链的发展情况并不尽如人意,企业缺乏加入绿色供应链的积极性与主动性,政府的引导、激励举措效果不显著等问题凸显,但是,关于我国建筑业绿色供应链激励体系问题的研究却鲜有。本研究以政府及参与供应链的企业为研究对象,构建了演化博弈模型,探讨了不同初始环境下,激励政策对建筑业绿色供应链中政府与参与主体行为策略的影响,考察政府及企业的行为演化规律,为制定建筑业绿色供应链激励优化策略提供理论依据。
1 建筑业绿色供应链中政府与企业的演化博弈分析
1.1 模型相关参数与假设
对于文中研究的建筑业绿色供应链中政府与企业的互动行为,做出如下假设:选取政府与企业作为博弈双方,政府率先作出决策,选择对企业进行强激励还是弱激励;企业则根据政府的选择作出响应,选择加入或者不加入建筑业绿色供应链;政府的强激励是指政府对企业采取直接的经济补贴、约束性较强的规定政策等激励手段。弱激励是指政府对企业采取间接的政策引导,倡议企业加入建筑业绿色供应链,而没有采取直接的激励手段。政府在对企业采取强激励政策时,政府的成本为Cg+C'g;采取弱激励政策时,其成本为Cg;政府采取强激励政策时,政府的收益为R2+Eg1-Cg-C'g;此时,企业选择加入建筑业绿色供应链时除获得自身创造的经济收益以外,还会获得企业在社会及行业中树立优秀品牌及良好商誉的无形收益以及政府给予的经济激励,同时也要付出一定的增量成本,因而企业的收益为R1+F+C'g-C;选择不加入时的收益为R'1;政府采取弱激励政策时,政府的收益可以表示R2+Eg3;此时,为企业选择加入建筑业绿色供应链时企业的收益主要包括企业自身创造的经济收益以及在社会及行业中树立优秀品牌及良好商誉的无形收益,同时也要付出一定的增量成本,因而企业的收益为R1+F-C;选择不加入时的收益为R'1。
其中,R1,R'1分别为企业选择加入和不加入建筑业绿色供应链时,企业所获得的经济收益;R2,R'2分别为企业选择加入和不加入时,政府所获得的经济收益,主要是指财税收益;F为企业选择加入后所得到的商誉、品牌收益;C为企业选择加入需要的增量成本;Eg1在较强的激励政策下企业选择加入所带来的社会收益与环境效益;Cg为政府行政成本;C'g为政府对企业进行经济激励时需要的经济成本;Eg2在较弱的激励政策下企业主动选择加入为政府带来的社会收益与环境收益。
假设,政府针对企业采取强激励政策的概率为x(等同于地方政府群体中采取强激励政策占地方政府总数的比例),采取弱激励政策的概率为1-x,企业选择加入建筑业绿色供应链的比例为y(等同于建筑业企业群中选择加入的企业占企业总数的比例),选择不加入的比例为1-y,可构建如表1政府与企业之间关于建筑业绿色供应链的2×2非对称演化博弈模型。
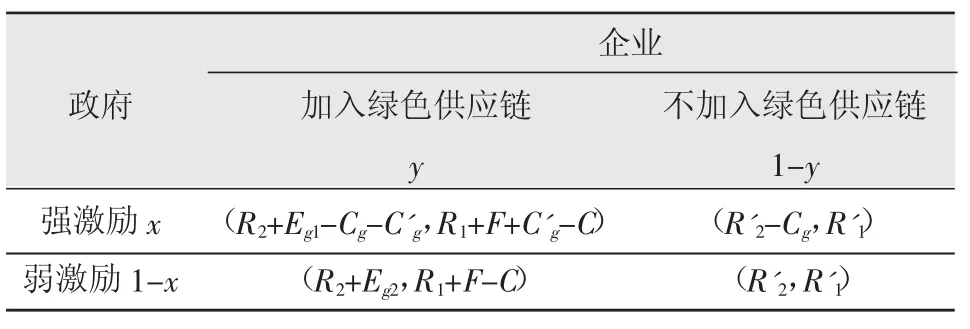
表1 政府与企业的演化博弈矩阵
由表1可得,政府采取强激励政策时的期望收益、政府采取弱激励政策时的期望收益、平均期望收益分别用Ua1,Ua2和表示,可得如下结果为:


企业选择加入绿色供应链的期望收益、选择不加入绿色供应链的期望收益和平均期望收益分别用Ub1,Ub2和表示,可得如下结果:

下面将利用复制动态方程分析政府与核心企业的演化稳定策略。
1.2 演化稳定策略分析
政府采取强激励政策的复制动态方程为:

企业选择加入绿色供应链的复制动态方程为:

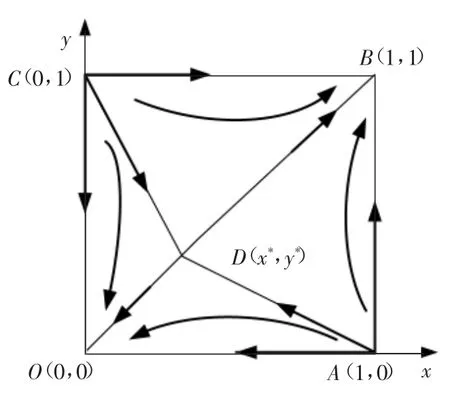
政府与企业对于建筑业绿色供应链博弈的演化可以用式(1)(2)两个复制动态方程表示。式(1)中,x1=0,1 或时,政府采取强激励政策的概率是稳定的;式(1)中,y1=0,1 或时,企业选择加入建筑业绿色供应链的比例是稳定的。
由 F(x)=0,G(y)=0,可得 5 个均衡点,其中:O(0,0),A(1,0)和 C(0,1),B(1,1),构成了演化博弈的边界,在内部还有均衡点 D(x*,y*),满足下面的方程组:

根据Friedman提出的方法,演化系统均衡点的稳定性可以由系统雅克比矩阵的局部稳定性分析得到[12]。

则该系统平衡点的局部演化稳定性有下列情形(表 2)。
情形 1:当 Eg1-C'g-Cg<Eg2,且 R1+F+C'g-C<R'1时,即政府采取强激励政策的期望收益小于弱激励政策的期望收益,且企业加入建筑业绿色供应链的期望收益小于不加入的期望收益。
情形 2:当 Eg1-C'g-Cg>Eg2,且 R1+F+C'g-C<R'1时,即政府采取强激励政策的期望收益大于弱激励政策的期望收益,且企业加入建筑业绿色供应链的期望收益小于不加入的期望收益。
情形 3:当 Eg1-C'g-Cg 表2 均衡点局部稳定性(情形1~3) 由表2可得,当政府与企业中有任何一方采取强激励政策的期望收益小于采取弱激励政策,或加入建筑业绿色供应链的期望收益小于不加入的期望收益时,仅存在4个局部均衡点,且演化稳定点为O(0,0),即政府采取弱激励政策,企业选择不加入建筑业绿色供应链。 (4)当 Eg1-C'g-Cg>Eg2,且 R1+F+C'g-C>R'1时,即政府采取强激励政策的期望收益大于弱激励政策的期望收益,且企业加入建筑业绿色供应链的期望收益大于不加入的期望收益,局部平衡点的稳定性如表3。 表3 局部均衡点稳定性分析(情形4) 由表3可得,当政府采取强激励政策的期望收益大于弱激励政策的期望收益,且企业加入建筑业绿色供应链的期望收益大于不加入的期望收益时,存在5 个局部均衡点,不稳定点 A(1,0)和 C(0,1),鞍点D(x*,y*),演化稳定点为 O(0,0)和 B(1,1),即政府采取弱激励政策,同时企业选择不加入建筑业绿色供应链;或政府采取强激励政策,同时企业选择加入建筑业绿色供应链了。 目前,我国建筑业绿色供应链还处于发展的初期阶段,同时建筑业绿色供应链的经济效益甚微,系统在较长时间内都将保持在两种状态并存的局面。政府与企业更偏向于采取弱激励和不加入。图1表示博弈双方关于建筑业绿色供应链建设的动态演化过程。 图1 政府与企业演化博弈相位图 尽管如此,结合政府与企业演化博弈的复制动态分析,可以看出,政府与企业的动态演化博弈也是有达到(1,1)均衡状态的可能性,但能否收敛于(1,1),取决于系统的初始状态落在图形OABC的哪个区域,不同区域的临界线有不稳定点A,C与鞍点D组成的连线决定。当初始状态落入临界线右上方ABCD区域时,演化系统将收敛于均衡点(1,1),即政府采取强激励政策,企业选择加入建筑业绿色供应链,双方达到理想的帕累托最优状态;当初始状态落入临界线左下方AOCD区域时,系统将收敛于(0,0),即政府采取弱激励政策,企业选择不加入建筑业绿色供应链,导致建筑业绿色供应链建设陷入难以推行的困境。 因此,政府与企业的演化系统不同的均衡结果取决于鞍点D(x*,y*),要促使政府与企业的博弈过程最终达到帕累托最优的均衡状态,必然要尽量扩大ABCD区域的面积,D点向左下方移动,即要使x*,y*的取值变小。由于参数较多,现从政府和企业两个角度分析,各相关参数的具体分析如下。 从政府与企业的演化博弈相位图可以看出,Cg越小,C'g越大,鞍点就越小,博弈双方初始状态落入区域ABCD的概率就越大。因此,综合考虑,若想既减小政府的财政压力,又对企业采取强效的激励政策,政府就要不断丰富激励手段,创新激励政策;Eg1越大,Eg2越小,鞍点就越小,博弈双方初始状态落入区域ABCD的概率就越大。因此,国家层面可以采取措施,提高针对建筑业绿色供应链进行激励的所产生的社会效益与环境效益,例如,政府可以通过构建建筑业绿色供应链信息发布平台,将建筑业绿色供应链的相关信息公开发布,以提高其产生的社会效益;R1越大,R'1越小,鞍点就越小,博弈双方初始状态落入区域ABCD的概率就越大。基于此,各地地方政府可以通过研发绿色技术、绿色施工工艺等手段降低加入建筑业绿色供应链的门槛,进而提高企业的经济收益;C越小,鞍点就越小,博弈双方初始状态落入区域ABCD的概率就越大。因此,如何降低增量成本成为政府部门必须解决的关键问题。例如研发绿色技术、绿色施工工艺等技术类措施和通过政府的容积率的奖励政策等降低企业的增量成本;F越小,鞍点就越小,博弈双方初始状态落入区域ABCD的概率就越大。为激励企业加入建筑业绿色供应链,政府可以通过建筑业绿色供应链信息发布平台,来扩大企业商誉及品牌的影响,促使企业选择加入建筑业绿色供应链。 对本章研究的建筑业绿色供应链中企业之间的合作行为,作出如下假设:选取企业A与企业B作为博弈双方,企业A率先作出决策,选择与企业B合作还是不合作,并确定合作深度;企业A则根据企业B的选择作出响应,选择合作或者不合作,并确定合作深度;当企业A与企业B均选择合作时,双方均可从合作过程中获得收益,收益包括4部分:合作带来的经济共享收益、政府给予的经济激励、合作成本、合作风险。企业双方均选择合作时,决定的合作深度会给企业带来不同的收益,同时,选择合作后所获得商誉、品牌激励也影响着合作双方的经济共享收益。企业A的经济共享收益为IaRbβ;IaD为政府给予的经济力;Ca-F为合作成本与风险;企业A的收益为IaRbβ+IaD-Ca-F。同理企业B的收益可以表示为IbRaβ+IbD-Cb-F。当企业A选择合作,而企业B选择不合作时,A和B的收益分别为{-Ca-F,IbRa-P}。由于企业A只是单方面选择合作,所以A无法获取经济共享收益,反而需要付出合作成本同时面临一定的风险,而B能够从A的合作中获取一定的收益IbRa,同时要受到惩罚P。同理可以得到当企业B选择合作,而企业A选择不合作时,双方的收益分别为IaRb-P,-Cb-F;当企业A和企业B都选择不合作时,即无法通过建筑业绿色供应链获得收益,因而双方收益均为0。 其中,Ri(i=a,b)为经济共享收益;D为企业在合作中取得了一定的社会效益与环境效益后,政府给予的经济激励;Ci(i=a,b)为企业双方不断了解,增加信任而付出的经济、人力、时间等成本;F为企业双方选择合作后需承担的风险;P为企业双方中的一方采取“搭便车”策略(不合作一方享受到合作方所带来的商誉、品牌效益)后所受到的惩罚;Ii(i=a,b)为企业双方在选择合作后,双方各自确定的合作深度。β为企业双方合作所能得到的商誉、品牌激励效用系数。 假设,企业A选择合作策略的概率为p(等同于群体A中选择合作的企业占企业总数的比例),则选择不合作策略的概率为1-p,企业B选择合作策略的概率为q,选择不合作策略的概率为1-q,其中,假定初始值确定。可构建如表4企业A与企业B之间关于建筑业绿色供应链的非对称演化博弈模型。 表4 企业A与企业B的演化博弈矩阵 由表2可得,企业A选择合作策略时的期望收益、选择不合作策略时的期望收益和平均期望收益分别用Wa1,Wa2和表示,可得如下结果: 企业B选择合作策略时的期望收益、选择不合作策略时的期望收益和平均期望收益分别用Ub1,Ub2,Ub表示,可得如下结果: 下面将利用复制动态方程分析企业A与企业B的演化稳定策略。 企业A选择合作策略的复制动态方程为: 企业A与企业B对于绿色供应链合作问题博弈的演化可以用以上两个复制动态方程表示。式(3)表示p1=0,1或时,企业A选择合作策略的概率是稳定的;式(4)表示 q1=0,1或 p=时,企业B选择合作策略的概率是稳定的。 由 F(p)=0,G(q)=0 可得 5 个均衡点,其中O(0,0),A(1,0)和 C(0,1),B(1,1),构成了演化博弈的边界,在内部还有均衡点,满足下面的方程组: 得: 根据Friedman[12]提出的方法,演化系统均衡点的稳定性可以由系统雅克比矩阵的局部稳定性分析得到:若矩阵的行列式值为正且迹为负,则局部均衡点为演化稳定策略(ESS);若矩阵的行列式和迹的值都为正,则为不稳定点;若矩阵的行列式值为负且迹为0或者不确定,则为鞍点。通过雅克比矩阵的局部稳定性分析,可得 2 个均衡点中不稳定点 A(1,0)和 C(0,1),演化稳定点为 O(0,0),B(1,1),鞍点为 D(p*,q*)。 我国建筑业绿色供应链目前尚处于初期发展阶段,参与企业的经济效益甚微。因此,企业A与企业B之间合作与否的博弈仍需要经历一段时期,双方的博弈系统在较长时间内都将保持在合作与不合作并存的局面。图2表示博弈双方关于建筑绿色供应链建设的动态演化过程。 图2 企业A与企业B的演化博弈相位图 结合企业A与企业B之间的演化博弈相位图,可以看出,企业A与企业B的动态演化博弈是有达到(1,1)均衡状态的可能性,但能否收敛于(1,1),取决于系统的初始状态落在图形O'A'B'C'的哪个区域,不同区域的临界线由折线A'D'C'决定。因此,鞍点D(p*,q*)就是影响博弈结果的关键点。演化博弈的最终收敛结果,将随着鞍点D移动而发生改变。鞍点D(p*,q*)的取值越小,区域A'B'C'D'面积越大,企业A与企业B合作的概率就越大。因此,各相关参数对双方合作的概率息息相关,具体分析如下。 从企业A与企业B的演化博弈相位图可以看出:Ci越小,鞍点越小,博弈双方初始状态落入区域A'B'C'D'的概率就越大。所以,应尽可能降低企业之间的合作成本;Ii越大,鞍点越小,博弈双方初始状态落入区域A'B'C'D'的概率就越大。应不断加深合作,推进建筑业绿色供应链的建设;当Ri增大时,鞍点会向区域左下角移动。因此,应不断加大双方合作的共享经济收益,构建合理的收益分配机制;鞍点位置随着β的增大而向区域左下角移动。激励措施产生越大的正向激励效用,对于促成企业A与企业B的合作的可能性就越大,所以,应加大对企业A与企业B的商誉、品牌激励;随着奖励参数D与惩罚参数P的增大,区域A'B'C'D'的面积也在增大,博弈向双方合作演变的可能性提高,表明政府对于建筑业绿色供应链的经济激励要确定合理的范围,负向激励与正向激励要相结合;F越小,相位图中区域A'B'C'D'的面积越大,企业A与企业B合作的可能性就越大,有效降低风险是促使企业A与企业B双方紧密合作的保证。 本研究运用了演化博弈理论分析了建筑业绿色供应链中政府与企业、企业与企业的行为互动过程,分析表明:在建筑业绿色供应链的激励体系中,政府部门需要率先做出引导、支持,在保证建筑业绿色供应链有效实现的前提,尽可能地为绿色供应链参与企业带来更多的经济收益。除了需要政府部门率先做出引导、支持外,核心企业也应起到带动绿色供应链链内其他参与企业、协调参与企业合作的作用。因此,在建筑业绿色供应链激励优化策略的选择上,就要突出政府部门的主导地位,强调政府与绿色供应链核心企业的激励互动关系;利用核心企业的主导地位,充分利用核心企业的主导、协调参与企业的地位。 基于此提出以下建议。 (1)明确政府的主导地位,着重与核心企业的激励互动。政府应以长期的社会和环境整体收益为出发点,准确把握自身的角色定位,引导绿色供应链核心企业去调动链内其他相关企业;积极推动财税经济激励政策创新,优化配置社会资源,弥补建筑业绿色供应链的外部性,调动核心企业的积极性,减弱核心企业的牵头激励的风险;积极推动建设建筑业绿色供应链相关法律法规和市场机制、适当的奖惩约束机制;搭建关于建筑业绿色供应链的政府信息发布平台和企业信息发布平台,推广宣传建筑领域绿色供应链。 (2)充分发挥核心企业的关键作用,协调各参与企业的分工合作、利益分配、冲突等,促进建筑业绿色供应链的有效实施;构建合理的合作成本分担与收益共享机制,提高其他参与企业的积极性,缓解成本、收益不均衡导致的参与企业动力不足问题,同时也可以降低核心企业率先参与绿色供应链的风险问题。 (3)建立与高等院校、科研院所的合作机制。利用高等院校、科研院所先天的学术资源与技术优势,不仅可以降低政府部门制定政策标准的成本,更能够不断开发绿色技术、绿色材料,从而弥补和降低核心企业率先加入绿色供应链的额外成本及风险。

1.3 模型参数分析及策略选择
2 建筑业绿色供应链中企业间的演化博弈分析
2.1 模型相关参数与假设

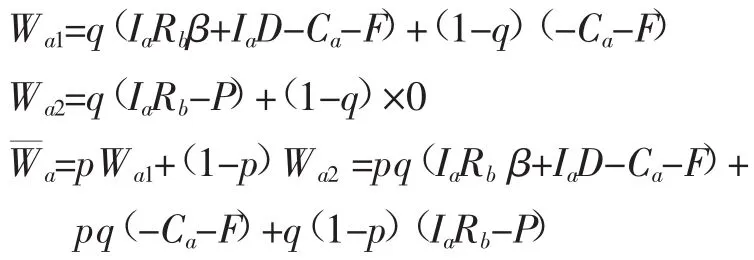

2.2 演化稳定策略分析



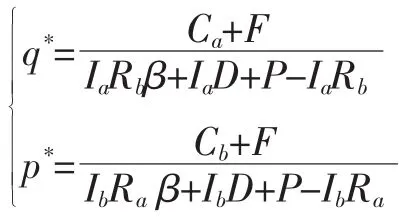
2.3 模型参数分析及策略选择

3 结论与建议
