基于损伤扩容理论的圆形隧洞围岩松动圈位移计算方法
2019-02-20沈才华古文博李鹤文张永进
沈才华, 古文博, 李鹤文, 王 媛, 张永进, 赖 勇
(1. 岩土力学与堤坝工程教育部重点实验室, 江苏 南京 210098;2. 河海大学土木与交通学院, 江苏 南京 210098;3. 浙江省水利水电勘测设计院, 浙江 杭州 310002)
0 引言
采用矿山法施工的隧洞开挖过程常采用动态监控量测法进行预警控制,其中,位移监控是主要方法之一,一般根据位移速率和总位移判别开挖过程中的安全性。因此,位移的预测就成为关键问题。目前关于位移预测的方法主要有3大类: 理论计算、规范经验性定值和数值计算。由于数值计算过程比较复杂,参数获取困难,所以在设计施工过程中还不普及,规范经验和理论计算方法仍占主导。
在理论计算方面,1938年,Fenner基于理想的弹塑性理论,将圆形隧洞分为弹性区和塑性区2个区域,假定塑性状态岩体在变形过程中体积保持不变进行位移求解,该方法未考虑塑性区体应变的影响,也没有反映围岩卸载变形破坏的特征,所求得的位移解析解不够精确[1]; Brown等[2]、Lee等[3]分别基于H-B准则和M-C准则,推导了支护应力与隧洞径向位移的理论公式预测隧洞松动位移,但塑性区围岩强度参数线性衰减的假设与实际情况有误差,而且不能反映破碎区卸载破坏的真实应力应变关系,也没有区分塑性区和破碎区。在国内,董方庭等较早提出了围岩松动圈支护理论,并通过实测位移多因素回归了巷道围岩收敛变形方程[4-5],具有很好的实用性,但对理论分析不够,对前期设计的指导意义有限; 李宁等[6-7]通过Fenner公式建立了能够综合反映地下洞室围岩变形模量、强度参数以及洞室埋深的围岩容许变形位移,并且讨论了不同洞形时公式的适用范围; 张黎明等[8]基于有限元强度折减法,分析了洞壁位移,并与限定位移值进行比较,以此来判别围岩的稳定性。目前未见根据现场实测卸载曲线预测围岩位移计算的成熟方法,因此,理论计算方法的实用性不强。
在规范经验方法方面,隧洞工程现行规范中对于岩石隧洞给出了允许的位移收敛量,并以此来判断围岩的稳定性[9]。规范提供的方法具有较为普遍的意义,但无论是埋深的限制范围还是容许位移的取值范围都比较大,给现场施工设计人员对于工程的安全预估带来不小的挑战。此外,规范对于位移的预测没有给出明确的规定,经验性参数太多,因此,导致预测不够准确,给隧洞施工安全带来很大的风险。
目前工程中运用的理论和规范计算方法预测结果与实际有误差,没有考虑围岩松弛开裂过程中的扩容是主要原因之一。本文在传统的Fenner公式的基础上,通过引入扩容系数k来模拟围岩在开挖时带来的体积扩容效应,并考虑不同松弛应力状态下围岩的不同扩容效应,采用分层总和法思想,简化围岩松弛变形积分计算,推导了基于圆形隧洞的围岩松弛位移计算公式,结合岩石破坏过程曲线特征,提出一个从理论上推求洞壁在开挖时容许位移和位移安全预警值的新思路,以期为设计和施工人员提供参考。
1 考虑扩容效应的洞壁位移理论计算推导
通常深埋或软岩隧洞开挖后围岩会出现松动破碎,此时可以把围岩分成3个区域,如图1所示。其中,pi为支护应力;r0为隧洞半径;rpb为塑性区半径;τpc为破碎区半径;r为某一点半径;ur为某一点位移;u0为洞壁位移;ub为弹塑性区交界面位移;uc为破碎区上边界位移; 带上标p的参数表示塑性区参数; 带上标e的参数表示弹性区参数; 带下标r的参数表示径向参数; 带下标θ的参数表示切向参数。

图1 围岩开挖力学模型
围岩在开挖前只受初始地应力的影响,假设这一状态下的围岩处于弹性阶段; 随着隧洞开挖卸载,在围岩的某一位置,当应力差σθ-σr达到某一强度值时发生塑性屈服,随着应力差的继续增加最终达到极限强度σ0,将围岩从屈服阶段到极限强度这一阶段定义为塑性区; 当继续卸载时,由于已经达到围岩极限强度,围岩开始破碎,强度也随之降低,此时拱轴线(即拱轴线处达到岩体极限强度)逐渐向围岩内移动,将围岩极限强度阶段到洞壁这一区域定义为破碎区。破碎区和塑性区由于岩石处于损伤累积状态,常表现为裂纹开裂的扩容现象。目前传统的Fenner公式没有考虑扩容效应,计算的围岩位移明显不符合实际情况,特别是破碎区扩容比较明显,扩容位移相对比较大,而且岩体的扩容系数与应力状态有关,因此,本文建立了考虑扩容效应的隧洞开挖围岩松动位移分层总和法。
1.1 基本假设
把围岩简化考虑,分为弹性区、塑性区和破碎区。在弹性区和塑性区不考虑扩容效应; 在破碎区考虑扩容效应,并假设破碎区扩容系数为常数,即采用等效扩容系数综合考虑扩容效应。基本假设如下: 1)围岩是均质、各向同性的介质; 2)岩体的力学特性符合弹塑性力学特征,塑性区服从Mohr-Coulomb屈服准则; 3)隧洞受静水压力作用,隧洞开挖属轴对称问题。
1.2 支护应力公式(Fenner公式)
假设岩体内的径向应力为σr,环向应力为σθ,径向应变为εr,环向应变为εθ。根据静力平衡条件∑r=0得出:
(1)
几何方程满足:
(2)
弹性区本构方程为:
(3)
(4)
式(3)—(4)中:E为弹性模量;μ为泊松比。
塑性区岩体采用Mohr-Coulomb屈服准则计算,最终可得到围岩塑性圈最大半径
(5)
式中:rpb为塑性区半径;r0为隧洞半径;p0为初始地应力;c′、φ′分别为内聚力和内摩擦角。
1.3 考虑扩容效应的位移解答
1.3.1 弹性边界的位移
弹性区的应变、位移关系遵循Hooke定律,因此,在弹、塑性区交界面上的位移ub为
(6)
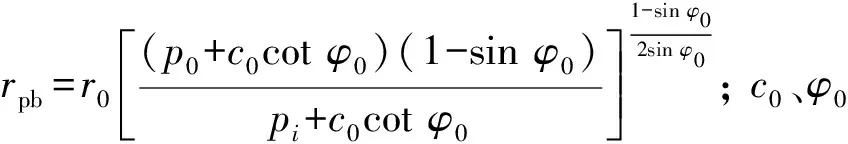
1.3.2 破碎区上边界的位移求解
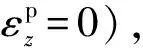
(7)
假设塑性区的岩体在变形过程中体积保持不变,则
π(rpb2-rpc2)=π[(rpb-ub)2-(rpc-uc)2]。
(8)
将式(6)的ub代入式(8),经整理得到
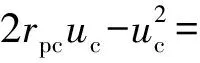
sinφ0(p0+c0cotφ0)rpb2。
(9)
再将式(5)代入式(9),得到:
(10)

对式(10)进行求解,得到破碎区上边界位移
(11)
1.3.3 开挖边界的松动位移计算
考虑塑性区扩容效应,引入扩容系数k,则
(1+k)π(rpc2-r02)=π[(rpc-uc)2-(r0-u0)2]。
(12)
将式(12)整理得到考虑松动区扩容效应的洞壁位移公式为
(13)

根据设计的支护压力可以计算塑性区范围,确定锚杆长度,并计算考虑扩容效应的围岩位移值,更加准确地预测隧洞最终位移,为开挖断面尺寸和隧洞预测变形量的确定提供参考。
2 基于分层总和法思想的围岩位移预测理论计算方法
2.1 假设条件
取隧洞埋深h处的围岩岩样做岩石加卸载试验,即取埋深h处的岩样,在围压γh条件下进行岩石加载,当达到峰值强度时(即假设压力拱轴线处岩石达到峰值强度)进行卸载试验,最终得到如图2所示的应力-应变关系图。本文将试验曲线图近似为原始隧洞应力-应变曲线图。
在第1节的分析中把松动圈的扩容效应系数等价为常数,误差较大。实际围岩塑性区包括了松动区,其扩容系数与应力状态有关。根据压力拱理论,可以把围岩分成弹性区、塑性区、破碎区3个区,如图3所示。弹性区、塑性区、破碎区分别对应应力-应变曲线AB段、BC段、CD段。由于在拱轴线内侧,岩体出现破碎损伤,强度降低,扩容才开始明显,对于塑性强化区(图3中的BC区域),进行简化处理,不考虑扩容效应。因此,取压力拱轴线为考虑扩容效应的起始边界(图3中的C边界)。另外,图2中的扩容起始点kr与图3中的kr点相对应,图2中点1和点2与图3中的点1和点2对应,显然点1和点2的扩容系数是不同的。因此,取径向单位宽度进行计算。假设单位宽度的扩容系数近似为常数,则该单位宽度层的变形量可以采用式(13)计算。因此,在塑性区范围内,从弹塑性边界到洞壁边界的位移积分就可以简化为采用基于分层总和法的围岩位移计算公式,具体推导见2.2节。很明显这样预测围岩的位移更符合实际情况。

图2 应力-应变关系图

图3 围岩分区示意图
2.2 考虑分层扩容效应的洞壁位移理论计算
围岩在弹性区和塑性区不考虑扩容效应。在破碎区由于岩石的碎裂破坏导致岩石的体积变大,且径向半径越小,破碎效果越明显,因此,在围岩的破碎区考虑扩容效应。
基于Fenner公式的弹塑性推导,采用极坐标表示的应力场分布为
(14)
(15)
由于开挖后隧洞收敛挤压力σθ实际是大主应力σ1,σr是小主应力σ3,因此,(σθ-σr)是与圆心距离r有关的表达式。则定义(σr-σθ)为r的函数f(r),即

(16)
根据式(14)、(15)计算的隧洞围岩内部距圆心r处的不同应力状态,结合室内卸荷试验得到的(σ1-σ3)~εv曲线,可以确定围岩松动圈内部不同位置对应的扩容体应变εv。

(17)

根据式(17)得到破碎区不同位置处的扩容系数,理论上沿径向采用积分计算便可获得累积位移量,但积分计算方法比较复杂,因此采用分层总和法简化计算。破碎区分层示意图如图4所示。假设在单位宽度内的扩容系数为常数,理论上单位宽度趋于0时分层累积计算接近于积分计算结果。根据分层迭代法思想,第i层内侧的位移公式递推过程如下。
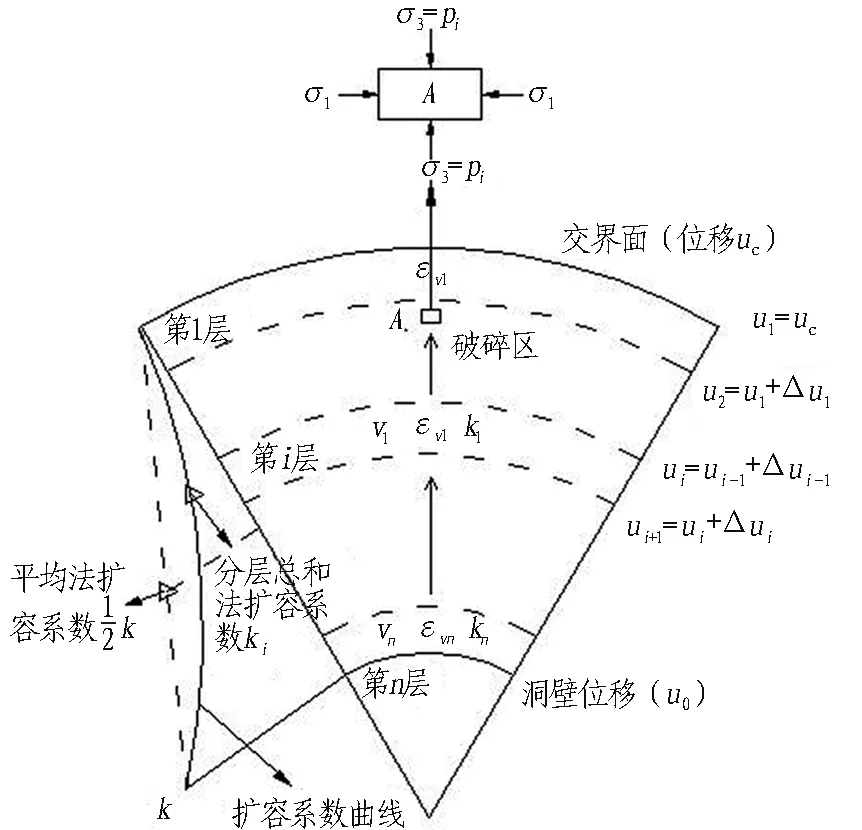
图4 破碎区分层示意图
将塑性区域分为n层圆环,如图4所示,每一层厚度
(18)
对于第i层,第i界面和第i+1界面半径分别为ri和ri+1,则
(19)
对于第i层,第i界面和第i+1界面位移分别为ui和ui+1,则根据式(12)位移递推公式可得:
ui+1=ui+Δui。
(20)
(21)
将式(21)从i=1到i=n进行求和,得到:
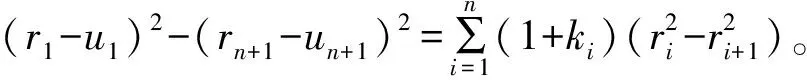
(22)
由于满足连续性假设以及弹性区满足Hooke定律,则有
u1=uc。
(23)
经过n次迭代后,可以迭代累积计算出洞壁处位移un+1(u0)。
(24)
(25)
3 围岩容许位移和安全预警值确定新方法
在实际的隧洞施工建设过程中,开挖部分的岩体处于卸荷状态。卸载条件下的岩体变形和破坏机制与加载条件下的岩体变形和破坏机制有着本质的不同,岩体表现出的力学特性也有很大的区别[10-13]。因此,选用卸荷试验的结果作为基础,判断容许位移和安全预警值。在实际情况中,岩石承受压力差是客观存在的,而且在长期的压力差作用下,岩石加载部分的变形已经完成。因此,可以将加载引起的变形忽略不计,只研究卸围压过程中引起的变形,并假定这部分变形从零开始[14-16]。由此可以得到各岩样仅由围压卸荷引起的应力-应变曲线。
结合其他学者的研究成果[17],取典型的岩石卸荷试验曲线,如图5所示。无量纲化处理之后,作出该曲线的曲率曲线(如图6所示),取曲率对应的体积应变,并以此来求整个塑性区的扩容系数k值。

图5 忽略初始变形的卸围压阶段应力差-体应变曲线
Fig. 5 Curve of stress difference-volume strain under unloading stage of surrounding rock without considering initial deformation
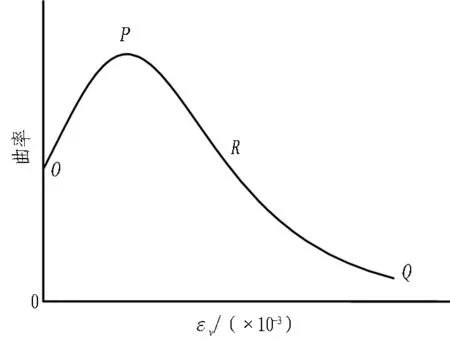
图6 应力差-体应变曲线的曲率曲线
由图6可知,扩容过程可以分成OP、PR、RQ3个阶段。岩石不同扩容程度表示了内在的不同状态,因此,建议把不同的扩容状态作为位移安全控制的参考值。由于理论上围岩内每处的扩容状态都不相等,建议以开挖洞壁处扩容状态为预警判别的依据,围岩内不同深度处的扩容系数可以根据室内试验确定,即通过室内试验可以获得曲线(图5)不同应力状态的扩容系数,进而采用分层总和法进行计算,预测洞壁处预警扩容值对应的预警位移值,弥补规范的位移控制值区间大、实际很难取值的缺陷,为位移安全控制值的设计提供简单可行的计算方法。
4 实例计算
4.1 扩容系数对围岩位移的影响分析
以分水江马蹄形隧洞断面(如图7所示)为例,将其简化为半径3.7 m的圆形隧洞断面。因为围岩的等效扩容系数与围岩松动程度和围岩力学性质有关,所以马蹄形隧洞围岩和圆形隧洞围岩的等效扩容系数不相同。研究不同等效扩容系数和不同埋深条件下围岩的位移变化规律,为预测变形量和隧洞开挖设计断面提供参考。

图7 分水江马蹄形隧洞断面图 (单位: cm)
Fig. 7 Horseshoe-shaped cross-section of Fenshui River Tunnel (unit: cm)
4.1.1 不同等效扩容系数条件下围岩位移变化规律
岩体的扩容过程反映了岩体的松动程度,同时,岩体的扩容状态与注浆、锚喷支护有关。因此,可以采用不同扩容系数来表示隧洞开挖受不同扰动、支护条件下的不同扩容状态。以Ⅱ、Ⅲ、Ⅳ、Ⅴ级围岩为例,分别利用式(13)计算围岩位移。由于是模拟开挖时隧洞围岩的松动状态,因此,假设隧洞支护应力为0。
根据《岩土锚杆与喷射混凝土支护工程技术规范》[9]得到岩石参数,如表1所示。

表1 岩石参数
不同围岩级别条件下洞壁位移u0与扩容系数k的关系曲线如图8所示。在100 m埋深下,Ⅱ、Ⅲ、Ⅳ级围岩的洞壁位移依次增大,并且围岩级别越大,围岩扩容对于位移的影响越大。同时,考虑扩容系数以后,位移变化明显增大,说明扩容效应对于位移的计算结果影响很大,而实际松动圈扩容效应是明显的。

图8 不同围岩级别条件下洞壁位移u0与扩容系数k的关系曲线
Fig. 8 Relationship between tunnel wall displacementu0and dilation coefficientkunder different rock grades
针对Ⅴ级围岩,对于扩容效应严重的地层,如果不进行加固支护,围岩将无法稳定,理论计算无法求解(实际可能已经塌方),此时建议采用加固后的设计参数进行变形量的预测。
4.1.2 不同埋深情况下围岩位移变化规律
以Ⅳ级围岩为例,分别计算埋深h为55、100、200、300、400 m时隧洞洞壁的位移变化规律,假设无支护开挖,Ⅳ级围岩的计算参数如表1所示,计算结果如图9所示。
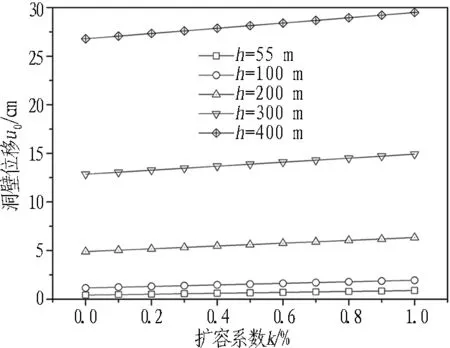
图9 不同埋深情况下洞壁位移u0与扩容系数k的关系曲线
Fig. 9 Relationship between tunnel wall displacementu0and dilation coefficientkunder different burial depths
由图9可知,对于同一级别的围岩,埋深越大,扩容效应对位移的影响越大。因此,对于埋深大的隧洞,更不能忽略由围岩扩容带来的影响。
针对Ⅳ级围岩,在进行无支护开挖时,洞壁位移与扩容系数、埋深以及围岩力学特性有关,可以用式(26)表示。
u0=f(k,h,α)。
(26)
式中α为围岩材料参数,代表E、μ、c、φ等。
对于分水江隧洞实际工程,可以认为参数α的影响相同。因此,开挖后主要影响因素为埋深h和扩容系数k。以Ⅳ级围岩为例,根据计算结果得到拟合回归公式为

(27)
采用式(27)提出的洞壁位移u0与埋深h和扩容系数k的函数关系,为分水江隧洞开挖洞形尺寸及位移预测提供了参考,同时也可以为类似工程提供借鉴。
4.2 预警值计算实例
以千岛湖输水隧洞砂岩段为例,埋深取100 m,简化半径为3.7 m。根据地质勘察资料,围岩级别为Ⅳ级,岩石物理力学参数见表1。
参考韩铁林等[17]对于砂岩卸荷力学试验的研究成果,取卸载破坏部分试验数据,则忽略初始变形的砂岩卸围压阶段应力差-体应变曲线如图10所示。
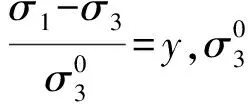
采用不同方法计算的洞壁位移u0与扩容系数k的关系曲线如图11所示。由于洞壁支护力pi(即初期支护力)不同,洞壁岩石的应力状态也不同,洞壁支护力越小,洞壁围岩破碎的扩容系数越大,围岩位移越大,考虑扩容效应的位移计算值明显大于弹塑性理论计算值。因此,考虑扩容效应更符合实际情况。弹塑性理论计算太保守,分层总和法可以考虑围岩不同应力状态下的扩容系数非线性,更符合实际情况。根据本工程算例可知,采用平均扩容系数得到的计算结果误差不大。

图10 忽略初始变形的砂岩卸围压阶段应力差-体应变曲线
Fig. 10 Curve of stress difference-volume strain under unloading stage of surrounding rock without considering initial deformation
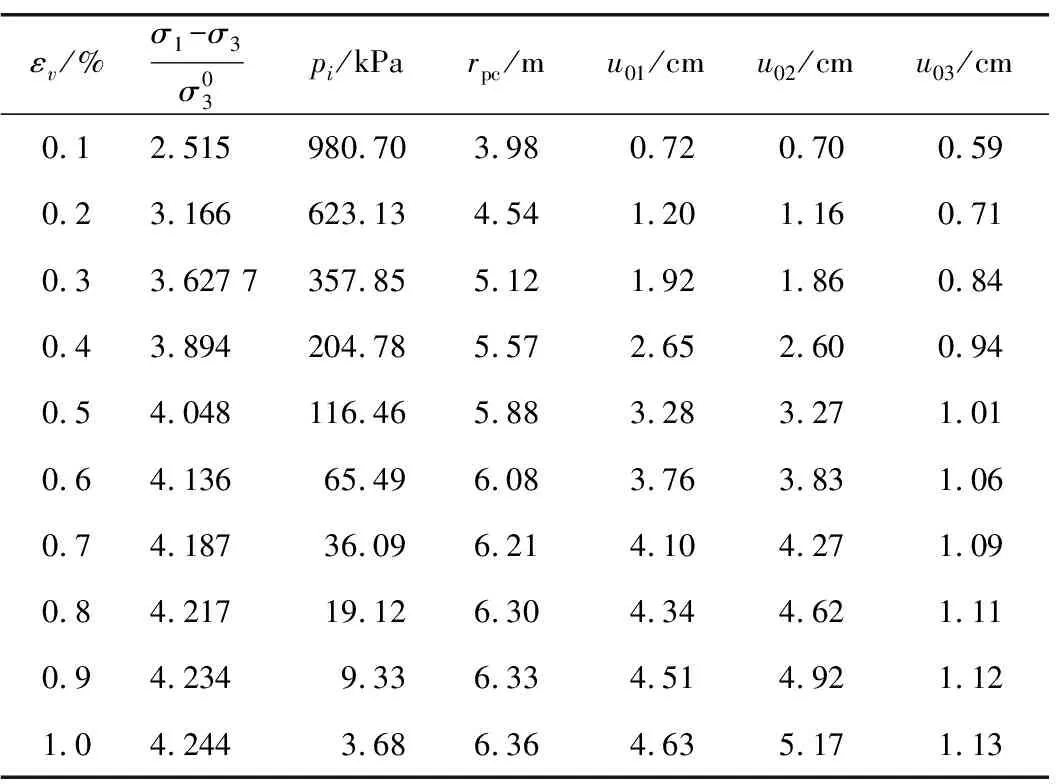
表2 位移计算结果
注:u01表示考虑扩容条件下采用分层总和法计算所得的洞壁位移;u02为考虑扩容条件下扩容系数采用平均值计算的洞壁位移;u03为不考虑扩容影响采用弹塑性理论(Fenner公式)计算所得的洞壁位移。
假设围岩破碎后块体未掉落,图11中的横坐标是不同支护应力下所对应的扩容系数,也可理解为不同支护应力下洞壁处围岩的碎胀程度(支护应力越大,洞壁处围岩碎胀程度越小),所计算得到的洞壁位移值为该隧洞预警位移值(在第3节已说明)。另外,通过式(24)并结合现场位移值的量测,还可以反算出围岩的等效扩容损伤区范围,为围岩加固和支护设计提供参考。

图11 采用不同方法计算的洞壁位移u0与扩容系数k关系曲线
Fig. 11 Relationship between tunnel wall displacementu0and dilation coefficientkcalculated by different methods
5 结论与讨论
1)洞壁围岩是隧洞开挖过程中稳定性控制的主要对象,其破碎稳定状态一般最差,因此,采用洞壁处围岩的扩容损伤状态作为预警状态比较合理。本文考虑围岩内不同应力状态的围岩扩容系数的非线性,建立了圆形隧洞围岩位移分层总和法计算方法,为考虑围岩扩容效应的位移理论计算提供了简单科学的方法,比弹塑性理论设计计算更符合实际情况,弥补了规范预警位移设计值取值范围大、缺乏科学理论依据的不足。
2)洞壁支护可以有效控制围岩的松动过程,对围岩内扩容损伤有一定的控制作用。支护力与围岩扩容状态一般呈非线性变化,通过本文提出的围岩位移分层总和法理论计算方法可以很好地反映支护-围岩位移-洞壁围岩损伤状态的协调关系,为支护设计提供参考。
3)结合实际工程分析了不同围岩级别、不同扩容系数k(即不同支护)、不同埋深等情况下洞壁位移理论计算值的变化规律,建立了分水江隧洞洞壁位移与埋深h和扩容系数k的经验计算公式,为实际工程的设计提供了参考。本方法可以为初步设计、施工设计提供参考,也可以结合动态反馈设计思想,为施工过程控制提供指导,计算方法可操作性强,较易推广,具有较强的工程应用价值。
4)在下一步的研究中,将引入数值分析手段,进一步验证该理论的正确性和实用性。
