平行隧道穿越形式对砌体建筑变形的影响研究
2019-02-20张稳军张友良
路 平, 耿 艳, 张稳军, 张友良
(1. 海南大学土木建筑工程学院, 海南 海口 570228; 2. 天津大学建筑工程学院, 天津 300072)
0 引言
截至2016年底,我国已有43座城市轨道交通规划获批,总规划里程超过8 600 km,且轨道交通建设有向二、三线城市延展的趋势,目的都是为了缓解老旧城区的交通拥堵。但在老旧城区中往往存在大量砖混、砖木结构的古旧建筑物,其中不乏重点保护建筑物,这些建筑物建成年代久远,在经历了风化、地震等不良地质现象后,无法像框架结构那样能够承受较大的不均匀沉降与倾斜。而在土层固结时间长且触变性大的软土地区,建筑物对不均匀沉降的适应能力更差,极易开裂甚至倒塌,引发社会矛盾。因此,当软土地区盾构隧道近接古旧建筑物施工时,建筑物的精细化变形控制显得尤为重要。
文献[1-3]分别利用三维有限元和有限差分方法模拟了盾构穿越建筑物的工况,得出建筑物刚度对地表位移有显著影响。文献[4-5]基于深圳地铁实测结果得出,盾构隧道走向与框架结构建筑物之间的夹角越小,建筑物沉降越大。文献[6]通过三维数值分析得出,建筑物中心偏离隧道中心一定距离且建筑物近隧道端位于隧道中心正上方时沉降最大。文献[7-8]基于土体损失计算理论,推导出建筑物的变形解析解,得出右线盾构完全穿越建筑物后,右线上方建筑物沉降稍大于左线。文献[9-10]结合现场监测结果,提出合理的注浆可对自重较小的建筑物的抬升有一定效果,纵墙裂缝主要分布于底层门窗处。文献[11]通过理论研究分析了盾构隧道下穿危旧建筑物的沉降规律,提出增加隧道埋深可有效减小建筑物的沉降。文献[12]针对双线盾构隧道平行、斜交下穿砌体房屋的沉降监测结果进行了研究,得出建筑物在盾构穿越不同阶段的沉降历时变化规律。
双线平行盾构隧道近接建筑物施工,2条隧道先、后的穿越顺序以及侧穿、下穿的穿越形式不同也均会对上方建筑物的变形产生差异影响。而国内外学者同时考虑穿越顺序与穿越形式对建筑物变形影响的研究相对较少,且对于砌体建筑物,倾斜为更敏感的控制指标。因此,本文结合天津地铁3号线和平路站至津湾广场站区间双线盾构隧道穿越砌体建筑物项目,采用三维数值模拟分析,辅以现场监测验证的方法,研究双线盾构隧道穿越顺序、形式对砌体建筑物沉降和倾斜的影响规律。
1 工程概况
1.1 隧道概况
和平路站至津湾广场站区间(简称和津区间)长度为478 m,采用2台直径6 390 mm复合式土压平衡盾构依次施工,2条平行隧道轴线距离约17 m。采用装配式钢筋混凝土管片衬砌错缝拼装,管片环宽1.2 m,厚350 mm。区间隧道最大坡度为17‰,隧道覆土厚度为12.6 ~21.6 m,隧道穿越范围内主要有⑥2粉土,⑦2粉土层,⑥1、⑦1粉质黏土以及下部⑦4粉砂层,下部粉砂层厚度约10 m。地下水为埋深约4 m的第四系孔隙潜水。
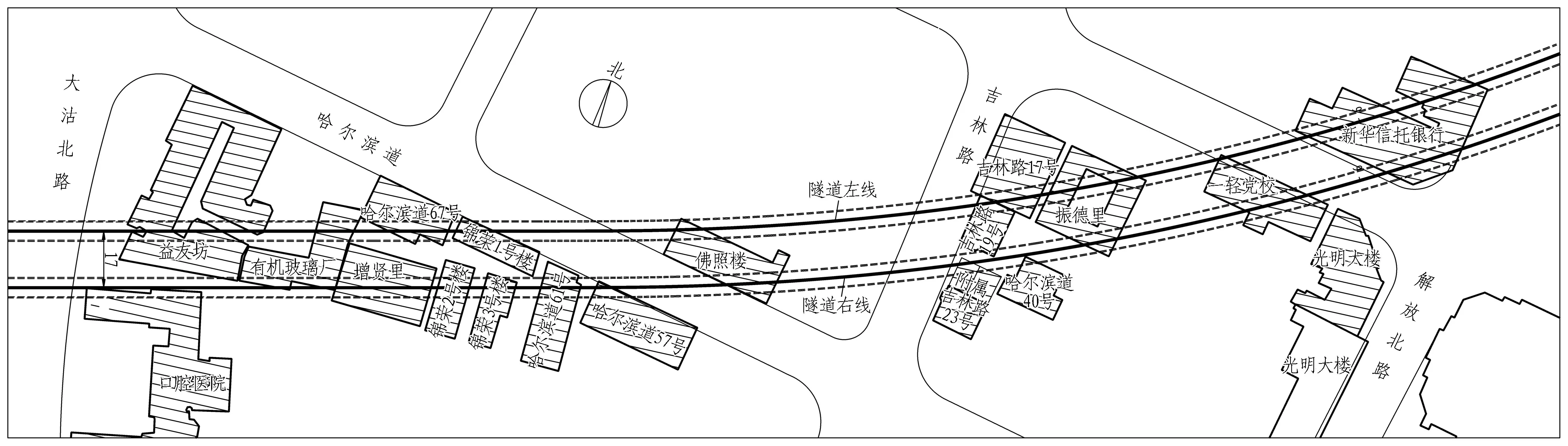
如图1所示,左线为先行隧道,第1台盾构于2011年1月26日从和平路站始发端出发,于2月19日掘进至建筑群(益友坊)处,此时左线已拼装了39环管片,4月19日通过建筑群(信托银行),到达津湾广场站接收端。右线为后行隧道,第2台盾构于3月1日从始发端出发,于3月18日掘进至建筑群(口腔医院)处,此时右线已拼装了30环管片,5月20日通过建筑群(信托银行),到达接收端。盾构在下穿建筑物期间,对建筑物每4 h监测一次并及时反馈,为下步施工提供依据。
(a) 平面图

(b) 纵断面图
1.2 建筑物概况
和津区间左、右线盾构始发后即穿越天津市主干道大沽北路,之后进入益友坊、增贤里等砌体建筑物。这些建筑物多为20世纪二三十年代修建,多为民宅,基础形式简易,埋深较浅,经历了唐山大地震及洪水灾害,现已严重风化、开裂,部分已为危房,如图2所示。现场对增贤里风化立柱周围增设了型钢支架支撑,并重新砌筑开裂墙根以增强稳定性,对佛照楼危房予以部分拆除,其他建筑不具备地面保护处理条件,主要通过隧道内注浆处理。

(a) 増贤里立柱风化

(b) 増贤里砖墙脱落
本研究拟选取和津区间的锦荣小区3座建筑物作为主要研究对象。这3座建筑物修建于同一时期,结构形式和基础形式相同,地层条件相近,下伏隧道埋深相近,便于分析比较。建筑物与双线隧道的平面位置关系如图3所示。根据水平面内建筑物纵墙与隧道走向的夹角定义盾构的下穿角度,当下穿角度接近0°时为小角度,接近90°时为大角度,即锦荣1号楼纵墙与隧道左线走向呈24°小角度斜交,锦荣2、3号楼纵墙与隧道右线走向呈74°大角度斜交。3座建筑物的概况见表1。

(a) 工况1

(b) 工况2
Fig. 3 Relative position between buildings and tunnels

表1 建筑物概况Table 1 Details of buildings
2 有限元模型
采用ABAQUS建立三维有限元模型,模型计算域尺寸和土体、隧道、建筑物的网格划分情况如图4所示。流固耦合模型采用soils的流体渗透应力耦合稳态分析步。土体采用多孔介质弹性模型与临界状态塑性模型(修正剑桥本构关系)的孔压单元模拟,参数通过室内试验[13]确定,其取值见表2,而土中流体则通过设置孔压边界条件来模拟排水条件。盾构、管片、同步注浆体均采用线弹性本构关系的实体单元模拟,其参数均与文献[13]中取值相同,其中同步注浆体采用“等代均质圆环”的方法模拟,而未考虑同步注浆压力的影响。由于这3座使用现状相近的建筑物均曾遭受地震作用,考虑其存在的内部损伤及开裂,均近似取墙体的弹性模量为220 MPa、泊松比为0.1,楼板弹性模量为30 GPa、泊松比为0.2[2]。

图4 有限元模型(单位: m)Fig. 4 FEM model (unit: m)
隧道掘进模拟采用“刚度迁移法”[13-14],每个掘进步长设为1.2 m(1环宽)。掌子面压力采用开挖面上沿深度线性增加的侧向压力来模拟,千斤顶顶推力采用平均施加在盾构、管片单元节点上的点荷载来模拟[13],且两者取值均根据该区间施工记录施加。
模型侧面、底面边界约束土体的法向位移;土体侧面边界地下水位以下施加梯度为10 kPa/m的静水压力; 不考虑隧道衬砌的渗漏,将衬砌在本研究中简化为不透水边界。
从表1实际工况(工况1)中的穿越形式来看,锦荣1号楼被2条平行隧道先下穿后侧穿,锦荣2、3号楼被2条隧道先侧穿后下穿。而在双线平行隧道穿越建筑物的线路确定后,这2种不同穿越形式对既有建筑物变形的影响仍是不确定的。因此,本文通过数值模拟的方法,又建立了穿越形式不同的对比工况2(见表1),即右线为先行隧道、左线为后行隧道。在工况2中,锦荣2、3号楼被2条隧道先下穿后侧穿,锦荣1号楼被2条隧道先侧穿后下穿。
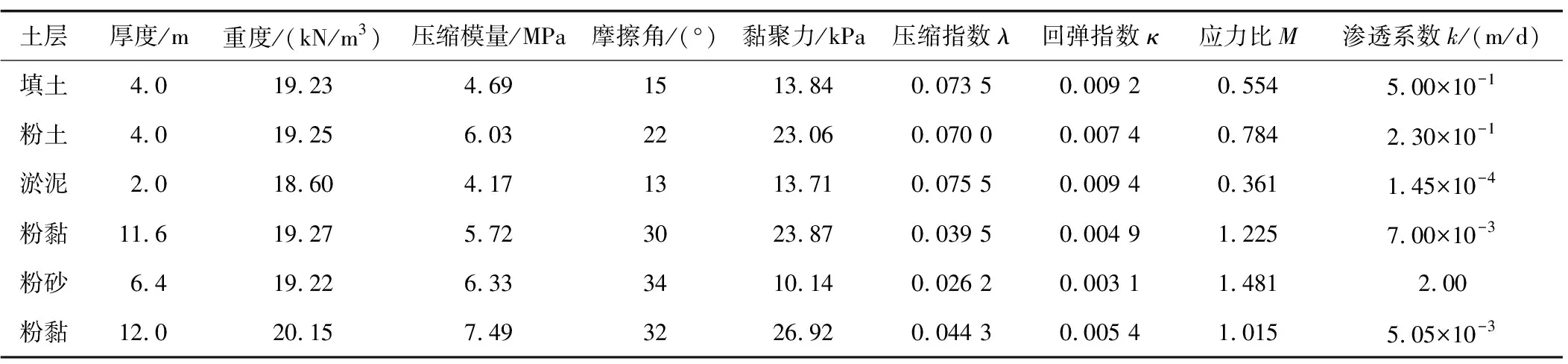
表2 土层参数Table 2 Parameters of soils
3 穿越形式研究
针对2种工况中穿越形式对3座建筑物变形的影响,本文从建筑物的沉降和倾斜率2个层面进行分析研究。
3.1 沉降
3.1.1 建筑物沉降规律
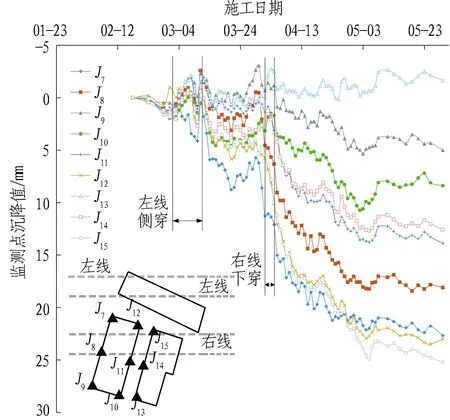
图5示出锦荣1号楼2个测点J1(隧道上方)、J5(隧道侧方)的实测沉降与计算沉降发展趋势。可以看出,计算沉降发展趋势与实测结果基本吻合,但J1处计算沉降值略大。这是由于实际工程中当盾尾脱出后,针对建筑物沉降较大处采取了二次注浆的抬升措施,因而建筑物沉降实测值比计算值偏小。
另外,1号楼在左线先行隧道下穿之后(3月1日)沉降迅速增大,各监测点的沉降速度约2.0 mm/d,处于规范[15-16]界定的地基危险状态。这种危险状态的形成,一方面是因为该建筑物基础形式本身非常薄弱,另一方面可由图6所示的计算应力土拱云图解释。图中R为Lee等[17]提出的竖向应力比,定义如下:
R= Δσz/σz。
(1)
式中:σz为竖向应力; Δσz为竖向应力的变化量。

图5 锦荣1号楼实测与计算沉降发展曲线(2011年)
Fig. 5 Measured and calculated settlement curves of Jinrong Building No.1 (in 2011)

图6 纵断面竖向应力土拱云图
土拱拱脚处R值大于0。由于土舱压力降低、盾尾地层损失使得隧道纵断面上的土体竖向应力重分布,形成了2个土拱,而左线盾构穿越过程中,在掌子面之前以及盾尾之后较大范围内,竖向应力比R均小于0,因而建筑物沉降增速随之增大。
建筑物沉降监测发展曲线如图7所示,建筑物墙体计算沉降曲线如图8所示。

(a) 锦荣1号楼
(b) 锦荣2号楼(左)、3号楼(右)
(a) 锦荣1号楼

(b) 锦荣2号楼
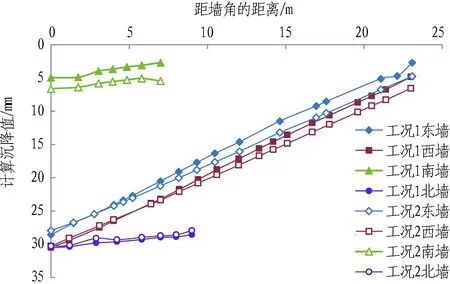
(c) 锦荣3号楼
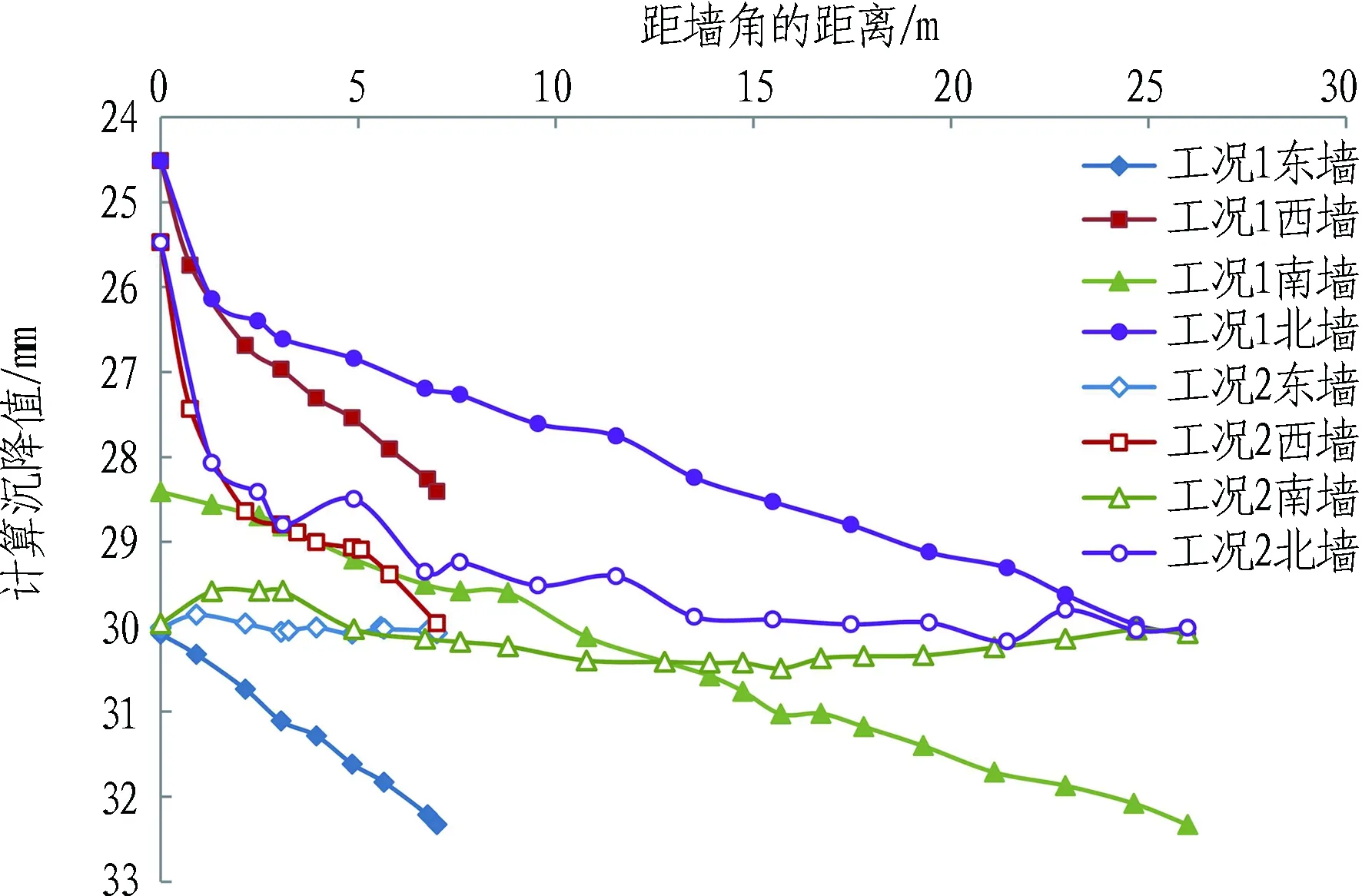
从图7(a)锦荣1号楼各监测点的沉降发展曲线和图8(a)各墙体的计算沉降曲线可以看出,当锦荣1号楼纵墙与隧道走向呈小角度斜交时,建筑物各点的最终沉降均较大,在2种工况下的最终计算沉降值都在25.0 mm以上。从图7(b)锦荣2、3号楼各监测点的沉降发展曲线和图8(b)、(c)各墙体的计算沉降曲线可以看出,对于隧道大角度斜交穿越的锦荣2、3号楼而言,在2种工况下建筑物各点的最终计算沉降值,较小的约2.0 mm,较大的接近25.0 mm。因此得出,当盾构小角度斜交下穿建筑物时,会产生较大的整体沉降[4];而当盾构大角度斜交下穿建筑物时,会产生较大的差异沉降[12]。
3.1.2 墙体沉降规律
图8(a)示出锦荣1号楼各墙体在2种工况下的计算沉降曲线。可得2种工况中各墙体的沉降规律各异,工况2中西、北墙的平均沉降值比工况1明显增大,平均增幅约2 mm(7%);而工况2中东、南墙的平均沉降值比工况1略小,平均降幅约1 mm(3%)。但对于每片墙体而言,沉降曲线形态在工况1中均趋于“单斜状”分布,而在工况2中更趋于“水平状”分布,其差异沉降在工况2中均明显低于工况1。即当建筑物纵墙与隧道小角度斜交时,先侧穿后下穿的穿越形式使得建筑物的差异沉降明显比先下穿后侧穿的穿越形式要小。
图8(b)、(c)分别示出锦荣2、3号楼各墙体在2种工况下的计算沉降曲线。可得2座建筑的沉降规律类似,工况2中东、西、南墙的平均沉降值比工况1明显增大,平均增量约1 mm,增幅5%~15%;而工况2中北墙的平均沉降值与工况1基本持平。对于每片墙体而言,2种工况中沉降曲线形态也基本一致,与隧道走向近乎垂直的东、西墙在2种工况中均趋于“单斜状”沉降分布,而与隧道走向近乎平行的南、北墙在2种工况中均趋于“水平状”沉降分布。即当建筑物纵墙与隧道大角度斜交时,2种穿越形式对建筑物的沉降值有一定影响,但对各墙体的沉降曲线形态的影响不明显。
3.2 倾斜率
砌体结构的开裂等与倾斜有更大关系,特别是这种古旧建筑物,整体性已较差,一旦倾斜对其危害更大。本文中对建筑物东、西墙的倾斜率以偏向南侧倾斜定义为正,对建筑物南、北墙的倾斜率以偏向西侧倾斜定义为正,反之为负。
3.2.1 墙体倾斜规律
从图9中3座建筑物的计算倾斜率可以看出,2种工况下锦荣1号楼墙体的最大计算倾斜率为0.36‰,而锦荣2、3号楼墙体的最大倾斜率约为锦荣1号楼的3倍。因此,盾构大角度斜交下穿建筑物时会使建筑物产生较大的倾斜。
此外,锦荣1号楼东、西墙的计算倾斜率是南、北墙的计算倾斜率的1.2倍以上;锦荣2、3号楼的东、西墙的计算倾斜率为南、北墙的计算倾斜率的3倍以上。这是由于3座建筑物的南、北墙和隧道走向基本上呈小角度斜交,如锦荣1号楼的南、北墙与隧道走向夹角约为24°,锦荣2、3号楼的南、北墙与隧道走向夹角约为16°,而东、西墙则呈较大夹角斜交。因此,当隧道掘进以不同角度斜交穿越建筑物时,与隧道走向夹角小的墙体倾斜会稍小,需对与隧道走向夹角大的墙体施加更严格的监控。
3.2.2 隧道穿越形式的影响机制
从图9(a)锦荣1号楼2种工况的倾斜率可以看出,锦荣1号楼各墙体在工况1中的倾斜率是工况2中倾斜率的2倍以上。因此,当隧道小角度斜交穿越建筑物时,工况1先行隧道下穿、后行隧道侧穿比工况2先行隧道侧穿、后行隧道下穿对建筑物明显不利。

(a) 锦荣1号楼

(b) 锦荣2号楼

(c) 锦荣3号楼
以上由隧道2种穿越形式诱发的建筑物差异响应可用地层损伤机制来解释,如图10所示。图10(a)、(b)分别为工况1中2条隧道刚通过y=115 m处横断面后的一个施工步内,土体竖向应力比R[17]的云图。可以看出,图10(a)中先行隧道盾尾脱出(t1)时,隧道的左右两侧均产生了很明显的竖向受压区(R>0),隧道的上下方均产生了明显的竖向受拉区(R<0),且由于上方建筑与隧道走向呈一定角度斜交,受拉区并不是沿隧道轴线对称分布的,因而先行隧道对地层的第1次损伤造成了上方建筑的第1次倾斜。图10(b)中后行隧道再次侧穿该建筑物且在盾尾脱出(t2)时,由于先行隧道的存在限制了后行隧道左侧的竖向受压区(R>0)的水平向发展,使其竖向受压区朝向地表延伸,但地表荷载始终未发生改变,因而引起地表附近地层再次产生了竖向受拉区(R<0)的第2次损伤,与第1次损伤一起共同加剧了先行隧道上方建筑物的倾斜。
另外,通过图11中隧道拱肩上方2点A、B的应力历史变化曲线可以得出,2种穿越形式中A点应力波动幅值最大发生在下穿隧道通过后,分别为20.4 kPa(t1)和20.3 kPa(t2),因而2种穿越形式对A点的应力波动幅值影响不大;2种穿越形式中B点应力波动幅值最大同样发生在下穿隧道通过后,分别为87.2 kPa(t1)和52.3 kPa(t2),即工况1中B点竖向应力的降幅约为工况2中的1.7倍,因而2种穿越形式对B点的应力波动幅值影响十分明显。这是因为对于B点来说,工况2为2条隧道依次先侧穿后下穿,侧穿的先行隧道会对两侧的土体产生侧向挤压,形成排水固结,对B点处地层起到了一定程度的加固作用,因而下穿B点的后行隧道由于地层损失产生的竖向应力的降幅较小。

(b) 工况1(右线后行隧道盾尾脱出时刻t2)

图11 土体的应力历史变化曲线Fig. 11 Development of soil stress
对于深度相同的A、B2点来说,2种工况中在侧穿隧道通过后,二者应力差接近,而在下穿隧道通过后,二者应力差较大。工况1中A、B2点在t1时刻应力差为23.9 kPa,而工况2中A、B2点在t2时刻应力差为16.8 kPa。较大的应力差将导致较大的沉降差,这也是工况1对应的穿越形式可导致下穿隧道上方建筑物产生更大倾斜的原因。
3.3 基础平面变形模式
基于2种工况建筑物的沉降与倾斜情况不同,对其基础平面的变形模式进行对比,如图12所示,图中变形比例为1∶1。可以得出,对于大角度斜交的锦荣2、3号楼,2种工况均未造成其基础平面形状的改变;而对于小角度斜交的锦荣1号楼,工况1中先下穿后侧穿的穿越形式造成了其基础平面产生了较明显的扭转,而工况2中几乎没有产生扭转。可见穿越形式的不同可以对建筑物基础平面的变形模式产生明显的影响。综上,实际工程中锦荣1号楼(小角度斜交)被隧道先下穿后侧穿的穿越形式,无论对该建筑物的倾斜还是基础平面变形模式的控制而言均为不利的工况。

(a) 工况1 (b) 工况2
4 结论与讨论
1)在被穿越建筑物规模已确定,且先后隧道施工控制水平稳定的前提下,盾构隧道会对与隧道平面走向夹角较小的建筑物产生较大的整体沉降;而对与隧道平面走向大角度斜交的建筑物产生较大的不均匀沉降及倾斜率。
2)当2条平行盾构隧道分别以小角度下穿和侧穿建筑物时,先行隧道下穿、后行隧道侧穿这种穿越形式使得建筑物各墙体沉降曲线趋于“单斜状”,而先行隧道侧穿、后行隧道下穿时建筑物各墙体沉降曲线则近似“水平状”。
3)当2条平行盾构隧道分别以小角度下穿和侧穿建筑物时,先行隧道下穿、后行隧道侧穿这种穿越形式使得建筑物下伏地层产生“二次损伤”,基础平面发生扭转,对建筑物倾斜率的影响约为先行隧道侧穿、后行隧道下穿时的2倍,对砌体建筑物更为不利。因此,当重点保护建筑物与平行隧道呈小角度斜交时,应尽量选择先行隧道侧穿、后行隧道下穿建筑物的穿越形式。
4)盾构以一定角度下穿同一建筑物,墙体被隧道以较大夹角穿越时的倾斜率稍大,约为夹角较小时墙体倾斜率的2倍。
当然,上述变形规律的得出是基于本文计算依托的实际工程进行分析而得到的。在该工程中,砌体建筑物规模和使用现状相近,土质条件相近,左右线隧道埋深相同且施工控制水平接近,隧道线路及其与建筑物的斜交角度已确定。在以上前提下,对建筑物沉降与倾斜的研究才得到上述隧道穿越形式的规律。如果建筑物结构形式不同,使用现状各异,2条隧道埋深不同,甚至为上下重叠隧道,则情况要复杂得多。对于这些更为复杂的情形,还需另外进行专门分析。
