基于TD-error自适应校正的深度Q学习主动采样方法

白辰甲 刘 鹏 赵 巍 唐降龙

(哈尔滨工业大学计算机科学与技术学院模式识别与智能系统研究中心 哈尔滨 150001)

强化学习[1](reinforcement learning, RL)是机器学习的重要分支.智能体在与环境的交互过程中根据当前状态选择动作，执行动作后转移到下一个状态并获得奖励.从智能体执行动作到获得奖励的过程产生了一条“经验”，智能体从大量经验中学习，不断改进策略，最大化累计奖励.传统强化学习方法适用于离散状态空间，不能有效处理高维连续状态空间中的问题.线性值函数近似或非线性值函数近似法将状态与值函数之间的关系进行参数化表示[2]，可以处理高维状态空间中的问题.其中，线性值函数近似有良好的收敛性保证，但往往需要人为提取状态特征，且模型表达能力有限；非线性值函数近似没有严格的收敛性证明，但具有强大的模型表达能力.Tesauro[3-4]将时序差分法(temporal difference, TD)与非线性值函数近似相结合，提出了TD-Gammon算法.该算法用前馈神经网络对状态值函数进行估计，在西洋双陆棋中达到了人类顶尖水平.

近年来，深度学习[5-6]与强化学习相结合[7]的非线性值函数近似方法在大规模强化学习中表现出良好性能.谷歌DeepMind团队提出了“深度Q网络”[8-9](deep Q-network, DQN)，DQN以图像序列作为输入，输出对动作值函数的估计，策略表示为卷积神经网络的参数.DQN在Atari 2600的大多数视频游戏上的性能超过了人类专家水平.

对经验样本的存储和采样是DQN的关键问题.DQN在训练中使用误差梯度反向传播算法，只有训练样本集合满足或近似满足独立同分布时才能正常收敛[10].然而，智能体与环境交互产生的样本前后具有强相关性.为了消除样本相关性，DQN使用经验池来存储和管理样本，在训练中从经验池中随机取样.DQN需要容量巨大的经验池(约106)，为了填充经验池，智能体需要频繁地与环境进行交互.然而，智能体与环境交互的代价非常昂贵的，不仅表现在时间的消耗上，更表现在安全性、可控性、可恢复性等诸多方面[11].因此，研究如何对样本进行高效采样、减少智能体与环境的交互次数、改善智能体的学习效果，对深度强化学习研究有重要意义.

目前针对DQN样本采样问题的研究主要有2个方面：1)并行采样和训练.使用多个智能体并行采样和训练，用异步梯度法更新Q网络[12-13]，其思想是通过并行采样和训练来打破样本之间的相关性.2)主动采样.强调样本之间的差异性[14]，为每个样本设定优先级，按优先级进行采样.Schaul等人[11]提出了优先经验回放法(prioritized experience replay, PER)，经验池中样本被采样的概率与样本的存储优先级成正比，存储优先级由经验池中样本上次参与训练的TD-error决定.TD-error是样本在使用TD算法更新时目标值函数与当前状态值函数的差值，其中目标值函数是立即奖励与下一个状态值函数之和.尽管PER算法在一定程度上提高了样本的利用效率，但在包含大量样本的经验池中，每个时间步仅有少量样本可以参与Q网络迭代，其余样本无法参与训练，这些样本的TD-error没有跟随Q网络的更新而变化，导致样本的存储优先级无法准确反映经验池中TD-error的真实分布.

为了进一步提高样本的采样效率，应当以更准确的采样优先级在经验池中选择样本.本文研究发现，经验池中样本距离上次被采样的时间间隔越长，样本的存储TD-error偏离真实值越远.由于长时间未被采样的样本数量巨大，导致存储优先级与真实优先级的偏差较大.本文提出一种基于TD-error自适应校正的主动采样模型(active sampling method based on adaptive TD-error correction, ATDC-PER).该模型基于样本回放周期和网络状态在样本与优先级偏差之间建立映射关系，实现对存储优先级的校正，在Q网络每次训练中都使用校正后的优先级在经验池中选择样本.本文提出的偏差模型参数是自适应的，在训练中模型始终跟随Q网络的变化，对采样优先级的估计更为合理.实验结果表明，校正后的优先级符合经验池中样本TD-error的分布，利用校正后的优先级选择样本提高了样本的利用效率，减少了智能体与环境的交互，同时改善了智能体的学习效果，获得了更大的累计奖励.

1 相关工作

1.1 强化学习

强化学习的目标是最大化累计奖励.智能体通过从经验中学习，不断优化状态与动作之间的映射关系，最终找到最优策略(policy).智能体与环境的交互过程可以用马尔可夫决策过程[15](Markov decision processes， MDP)来建模.在周期型任务中，MDP包括一系列离散的时间步0,1,2,…,t,…,T，其中T为终止时间步.在时间步t，智能体观察环境得到状态的表示St，根据现有策略π选择动作At并执行.执行动作后MDP到达下一个时间步t+1，智能体收到奖励Rt+1并转移到下一个状态St+1.回报定义为折扣奖励之和，智能体通过调整策略来最大化回报.动作状态值函数是指智能体处于状态s时执行动作a，随后按照策略π与环境交互直到周期结束所获得的期望回报，记为Qπ(s,a).

最优策略求解一般遵循“广泛策略迭代”的思想，包含策略评价和策略提升[1].策略评价是已知策略计算值函数的过程，策略提升是已知值函数选择最优动作的过程.策略评价中值函数Qπ(s,a)的求解可以使用贝尔曼方程[15]转换为递归形式

其中，r是立即奖励，γ是折扣因子.值函数定义了在策略空间上的偏序关系，存在最优策略π*优于(或等同于)其他所有策略.

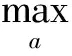
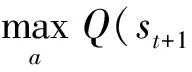
1.2 深度Q网络

深度Q网络[9](DQN)遵循Q-learning算法的更新法则，与线性值函数近似的不同之处在于DQN使用Q网络来表示动作值函数，进而表示策略.Q网络是由卷积层和全连接层组成的卷积神经网络(CNN).DQN的主要特点有2个：

1) 使用2个独立的Q网络.分别使用θ和θ-代表Q网络和目标Q网络的参数，每隔L个时间步将Q网络的参数复制到目标Q网络中，即θ-←θ，随后θ-在L个时间步内保持不变.DQN中TD-error定义为

(1)

2) 使用经验池存储和管理样本，使用经验回放[25]选择样本.样本存储于经验池中，从经验池中随机抽取批量样本训练Q网络.使用经验回放可以消除样本之间的相关性，使参与训练的样本满足或近似满足独立同分布.

在DQN的基础上，Hasselt等人[26-27]指出，DQN在计算TD-error时使用相同的Q网络来选择动作和计算值函数会导致值函数的过高估计，进而提出了DDQN(double DQN)算法.该算法用Q网络来选择动作，用目标Q网络来估计值函数，从而消除了对值函数的过高估计，并提升了智能体的累计奖励.DDQN中TD-error由式(2)计算：

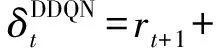
(2)

此外，一些研究从不同角度提出了DQN的改进方法，主要思路可以分为：1)从探索和利用的角度[28-31]，将传统强化学习中使用的探索与利用策略扩展到深度强化学习中，改进DQN中的ε-贪心策略.2)从网络结构的角度，使用竞争式网络结构[32]，分别估计动作值函数和优势函数.3)从并行训练的角度[12-13]，消除样本之间的相关性，同时加速训练.4)从减少训练中奖励方差的角度[33]，使用多个迭代步的延迟估计Q值，使其更加稳定.5)从模型之间知识迁移和多任务学习的角度[34-35]，扩展DQN的使用范围.6)从视觉注意力的角度，使智能体在训练中将注意力集中于有价值的图像区域[36].7)从主动采样，减少与环境交互次数的角度[11]，使用基于TD-error的优先经验回放来提高样本的利用效率.

1.3 优先经验回放

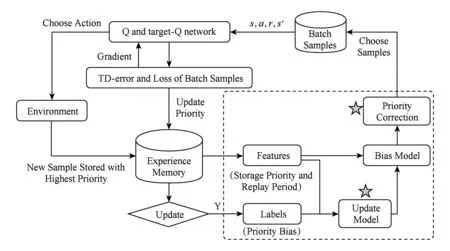
Fig. 1 The main architecture of ATDC-PER model 图1 本文方法(ATDC-PER)的总体结构

优先经验回放是一种有效的管理经验池的方法.原始的DQN算法在训练时不考虑经验池中样本之间的差异，随机抽取样本进行训练，导致样本的利用效率较低，智能体需要频繁地与环境进行交互.针对这一问题，Schaul等人[11]提出了优先经验回放法(PER)来估计每个样本的优先级，按照优先级选择样本训练Q网络.样本优先级由样本的TD-error分布决定.样本的TD-error绝对值越大，在训练中造成的Q网络损失越大，表明该样本给Q网络带来的信息量越大，在Q网络后续迭代中应“优先”选择该样本参与训练.PER算法的主要特点有3个：

1) 样本优先级基于样本上次参与训练时的TD-error值.长时间未参与训练的样本在经验池中存储的TD-error长时间未更新，这些样本的TD-error无法跟随Q网络的变化.只有上一个时间步参与训练的批量样本的TD-error值被更新，然而这部分样本仅占经验池中样本的少数.

2) 采样时在优先级的基础上引入随机性.完全按照优先级进行采样会降低样本的多样性，因此PER算法中引入随机性，使样本被抽取的概率与优先级成正比，同时所有样本都有机会被采样.

3) 优先级的引入相对于均匀抽样改变了样本的分布，引入了误差.PER算法使用重要性采样权重对误差进行补偿.在计算损失函数梯度时，需在原有梯度的基础上乘以重要性采样权重，按补偿后的梯度进行更新.

PER算法[11]具有高度的灵活性，可与离策略的深度强化学习方法进行广泛结合.例如，文献[37-38]将PER算法和策略梯度法结合，提高了确定性策略梯度算法[39-40](deep deterministic policy gradient, DDPG)在仿真机器人控制中的数据利用效率；PER算法与深度Q学习的结合提高了经验池中样本的利用效率，显著减少了智能体与环境的交互次数，提升了智能体的最优策略得分[11].

2 基于TD-error校正的主动采样模型

PER算法的问题在于，经验池中存储的TD-error值相对于Q网络来说更新不及时，无法准确反映样本的优先级.在每次迭代中Q网络都会更新自身参数，而经验池仅可更新参与训练的批量样本的TD-error值，此类样本的数量约占经验池容量的0.1%.这导致大多数样本的存储TD-error无法跟随Q网络的变化，并进一步导致样本在经验池中的存储优先级与“真实”优先级之间存在偏差.本文分析了这种偏差对学习的影响，并阐述了依据真实或逼近真实的TD-error分布产生的优先级来选择样本能够使深度Q网络以更高的效率收敛到最优策略.

本文提出基于TD-error自适应校正的主动采样模型(ATDC-PER)来校正样本的存储优先级，使用校正后的优先级分布进行主动采样，能够提高经验池中样本的利用效率.图1是本文方法ATDC-PER的总体结构，主要包括“偏差模型”和“优先级校正”两部分.其中，优先级校正需在所有时间步进行，偏差模型则每隔D个时间步更新1次.2.1节使用引例说明TD-error及样本优先级分布对学习的作用，2.2节阐述ATDC-PER的建模过程，2.3节给出算法描述和复杂度分析.

2.1 TD-error偏差分析

本节用强化学习中的经典问题平衡车[41](CartPole)为引例①https:gym.openai.comenvsCartpole-v0，说明PER算法中经验池的存储TD-error与真实TD-error之间存在偏差，并分析TD-error分布对学习的作用.

CartPole的状态表示为4维向量，包括杆的角度、杆运动的角速度、车的位置和车运动的速度，如图2所示：

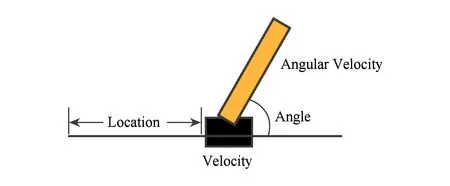
Fig. 2 The state of CartPole图2 倒立摆的状态表示

智能体通过向小车施加+1或-1的力来尽力保持杆的平衡.在时间步t，如果杆与垂直方向的角度不超过15度且小车与中心的距离不超过2.4个单元，则奖励为+1，否则奖励为-1同时周期结束.设1个周期的时间步不超过200步，则智能体在1个周期内所获得的最大奖励不超过200.用基于DDQN的PER算法来训练Q网络，Q网络是包含64个隐含层节点的3层全连接网络，经验池容量为50 000.

PER算法中经验池用样本集合E={e(1),e(2),…,e(m)}表示，其中序号为i的样本e(i)=s(i),a(i),r(i),s′(i)∈E.PER算法在每次迭代时抽取E中的1个批量样本进行训练.本文将样本e(i)上次参与训练的TD-error值称为样本的存储TD-error，记为δ(i).设当前时间步为t，e(i)上次参与训练的时间步为t-τ(i)，则δ(i)由式(3)计算[27]：

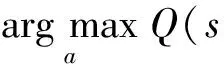
(3)

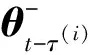
由式(3)可知，存储TD-error计算中使用的参数θt-τ(i)不是当前Q网络参数，而是τ(i)个时间步之前的参数.在τ(i)个时间步内Q网络经历了τ(i)次参数迭代，而存储TD-error值却保持不变.这导致样本的存储TD-error与当前Q网络不匹配，且τ(i)的值越大，这种不匹配程度越高.新样本加入经验池时τ(i)=1，每经历1个时间步，参与该时间步训练的样本τ(i)置1，未参与该时间步训练的样本τ(i)加1.由于经验池满后新样本会覆盖老样本，因此所有样本τ(i)的取值范围均在1到经验池样本总量之间.图3显示了CartPole在训练周期为420时经验池样本的τ(i)的分布，样本按τ(i)由小到大排序，经验池中样本总数为50 000.图3表明，经验池中有大量样本的τ(i)值较大，这些样本长期没有参与训练，δ(i)长期未更新.因此，存储优先级与当前Q网络的不匹配程度较高.

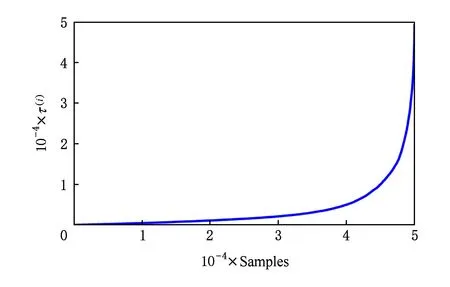
Fig. 3 Distribution of τ(i) in experience memory when training episode is 420图3 训练周期为420时经验池中样本的τ(i)的分布

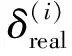
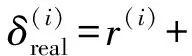
(4)

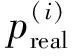
p(i)=(|δ(i)|+ε)α,

(5)

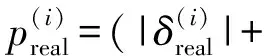
(6)

其中ε和α均为常数.样本TD-error的绝对值越大，在采样中样本的优先级就越高.

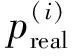
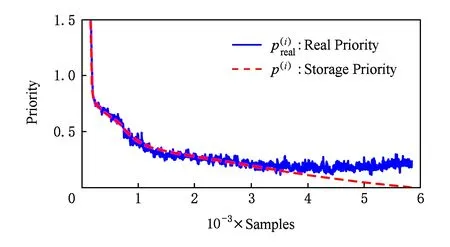
Fig. 4 Distribution of p(i) and in CartPole training when training episode is 180图4 CartPole训练周期为180时p(i)和分布图

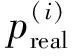
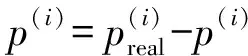
(7)

图5显示了优先级偏差的绝对值|Δp(i)|的分布，样本仍按照p(i)由大到小排序.

Fig. 5 Distribution of |Δp(i)| in CartPole training when training episode is 180图5 CartPole训练周期为180时|Δp(i)|的分布图

图4和图5表明，PER算法中使用基于δ(i)的存储优先级进行主动采样存在2个问题：

2)δ(i)的分布不能准确反映经验池的真实情况.其中，当|δ(i)|较大时，样本被抽取的概率高，τ(i)值较小，期间Q网络变化不明显，优先级偏差较小，此时可以使用存储优先级作为真实优先级的近似估计；但当|δ(i)|较小时，τ(i)值较大，Q网络在τ(i)个时间步内参数变化较大，导致存储优先级偏离真实优先级的分布，此时基于δ(i)的存储优先级不能准确反映经验池的情况.

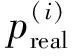
Fig. 6 Training curve comparison using experience replay with p(i) and 图6 使用p(i)和作为优先级的训练曲线对比

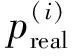
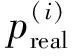
2.2 ATDC-PER模型

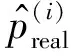
真实优先级和存储优先级的偏差分布具有稳定性，所以ATDC-PER方法对偏差模型更新周期D的选取是不敏感的.真实优先级与存储优先级的不同之处在于计算时使用的Q网络参数不同，真实优先级使用时刻t的Q网络参数，而存储优先级使用t-τ(i)时刻的Q网络参数，二者的区别在于τ(i)的分布.如图3所示，τ(i)在经验池中呈现长尾分布，最小值为1，最大值为经验池样本总量.在训练中经验池填充满后容量不再发生变化，τ(i)分布具有稳定性，因此偏差模型不需要频繁更新.

ATDC-PER算法在训练过程中偏差模型分段更新的示意图如图7所示，横轴代表训练时间步，纵轴代表智能体在周期内的累计奖励.偏差模型更新后的D个时间步内均使用该模型进行优先级校正，可以极大地减少时间开销.

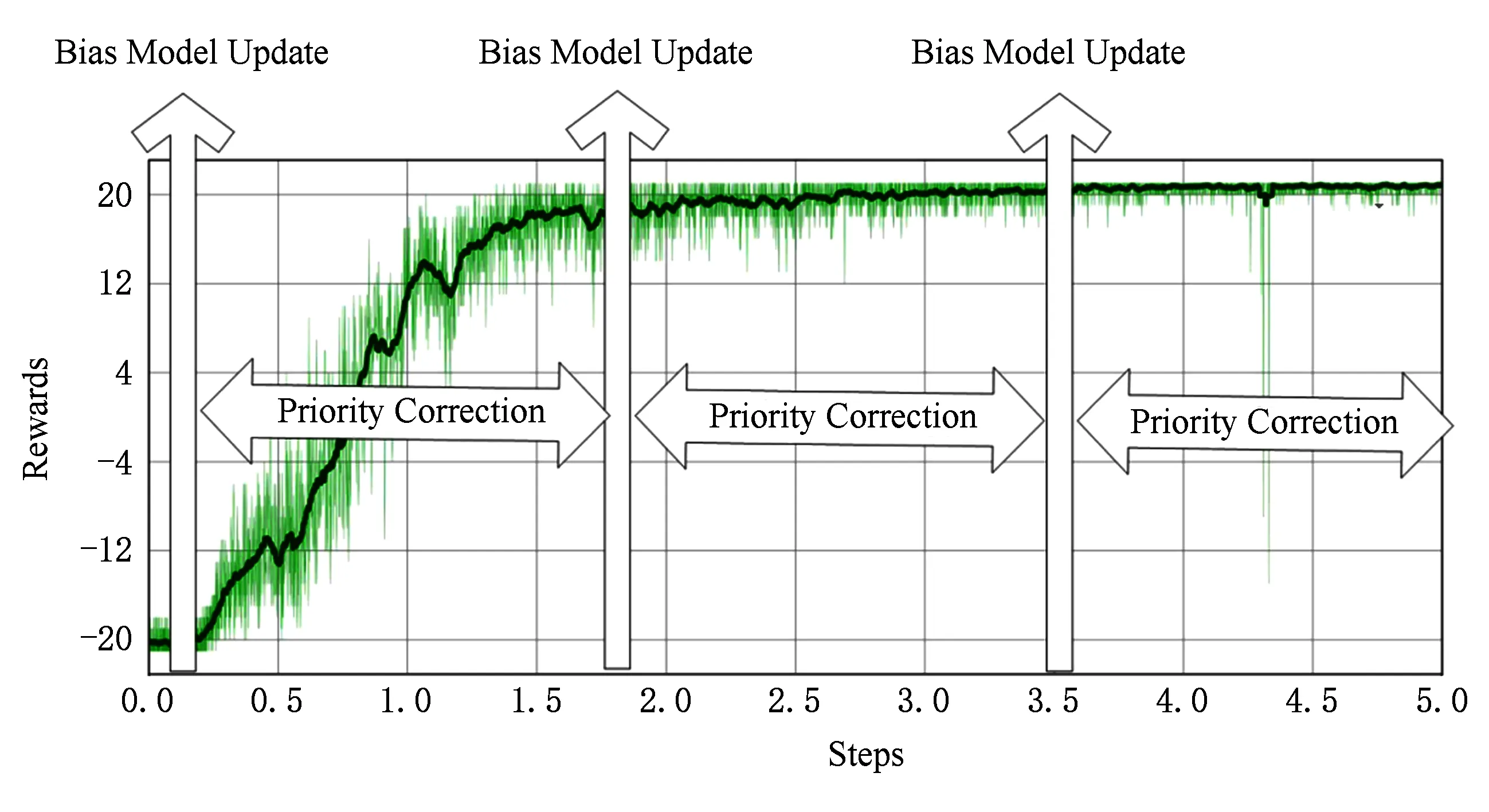
Fig. 7 Interval update policy in ATDC-PER algorithm图7 ATDC-PER算法的分段更新策略示意图

2.2.1 偏差模型

从经验池中提取的样本特征是偏差模型的输入，真实优先级和存储优先级之间的优先级偏差作为样本标签，是偏差模型的输出.使用线性回归模型对样本特征与样本标签之间的关系进行建模，通过最小化平方损失函数来求解模型参数w.

1) 样本特征.样本特征是针对单个样本而言的.特征在训练中的经验池中保存且与优先级偏差相关.样本特征包括：

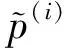
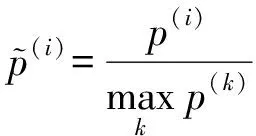
(8)

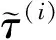
(9)

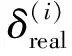
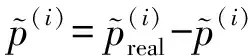
(10)

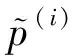
(11)

Atari游戏Pong①https:gym.openai.comenvsPong-v0和Breakout②https:gym.openai.comenvsBreakout-v0在训练时间步为105时经验池中所有样本的样本特征,和样本标签Δ的分布如图8所示，样本按照存储优先级排序，具体的设置将在实验部分介绍.图8表明，样本的存储优先级和回放周期都与优先级偏差Δ密切相关.

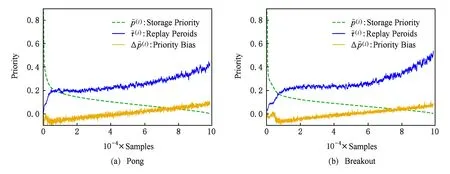
Fig. 8 Distribution of feature , and label Δ in Pong and Breakout when t=105图8 Pong和Breakout在t=105时样本特征,和样本标签Δ的分布

3) 偏差模型参数求解.使用回归模型来对样本特征和样本标签之间的关系进行建模.由于样本特征与样本标签之间的关系明显，因此使用线性回归模型.同时，线性回归模型在当前的输入输出条件下存在闭式解，不需要使用梯度法迭代求解，时间开销很小.

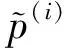
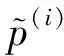
权重向量w的维度与特征x(i)的维度相同.根据线性回归模型的定义，假设函数hw(x(i))表示为

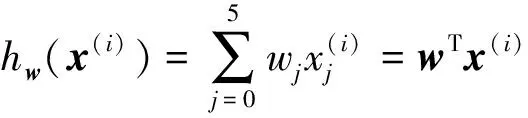
(13)

设当前经验池中样本数为m，则全体样本组成的特征矩阵X∈m×6，表示为

(14)

(15)

损失函数为平方误差损失，记为J(w).经验池中所有样本的平均损失表示为

(16)

参数向量w为使得损失J(w)取最小值的解.由于特征矩阵X的元素均大于0，w存在闭式解.经推导可得，最小化损失函数J(w)的w的解为

w=(XTX)-1XTy.

(17)

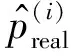
2.2.2 优先级校正

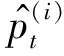
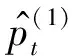
(18)

(19)

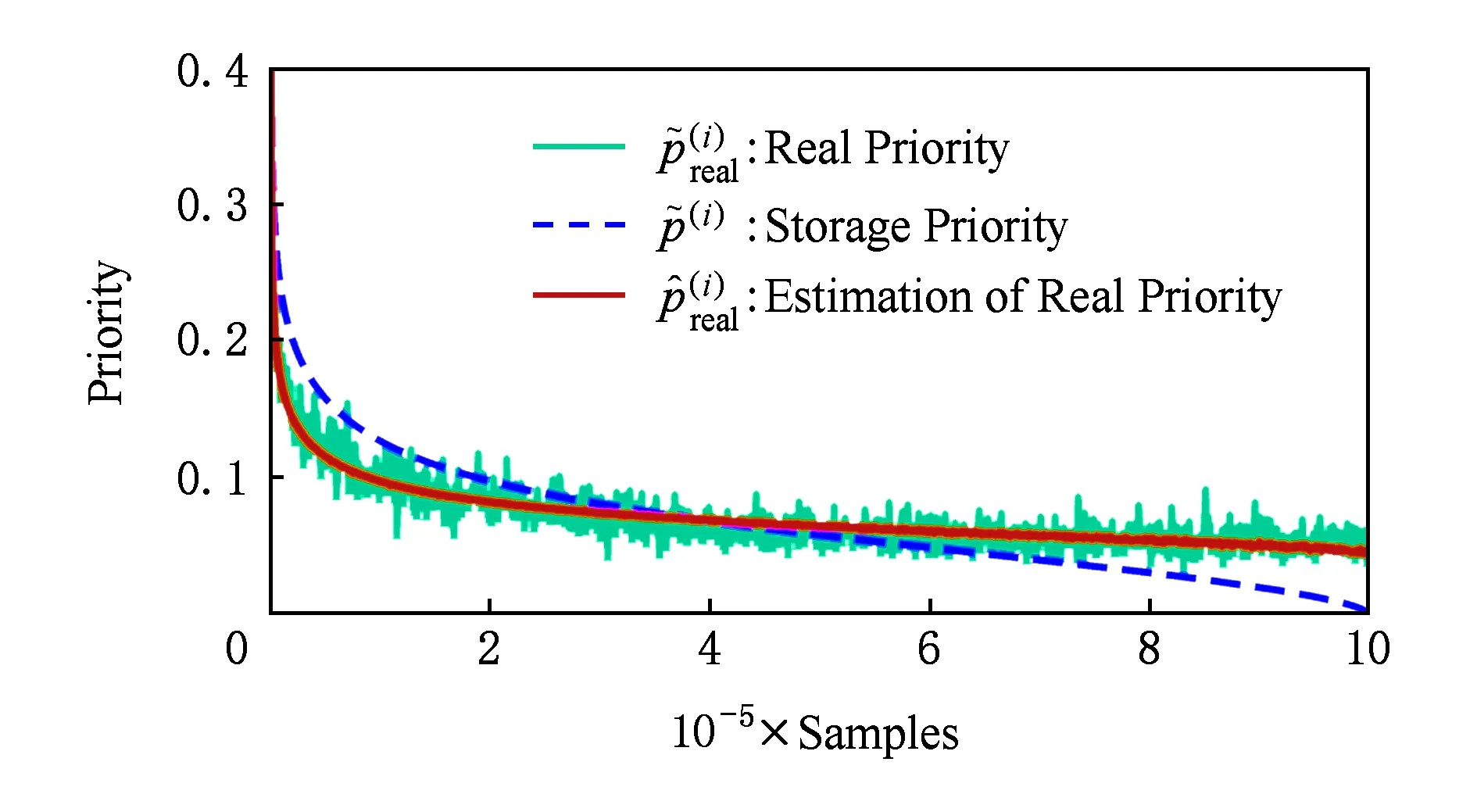
Fig. 9 Distribution of , and at step t=107 in Breakout training图9 Breakout训练中t=107时,和分布

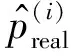
2.3 算法描述和复杂度分析

2.3.1 算法描述

ATDC-PER的算法流程如算法1所示.

算法1. ATDC-PER算法.

输入：偏差模型特征阶数K、偏差模型更新周期D、奖励折扣因子γ、样本批量大小k、学习率η、经验池容量N、偏差模型参数α、重要性权重β、训练终止时间步T、目标Q网络更新频率L；

输出：Q网络参数；

初始化：经验池为空，批量梯度Δ=0，初始化Q网络和目标Q网络参数为θ和θ-.

① 根据初始状态S0，以ε-贪心选择动作A0～πθ(S0)；

② fort=1 toTdo

③ 观察到状态St并获得奖励Rt；

④ 将经验序列(St-1,At-1,Rt,St)存储到经验池中，并赋予当前经验池中最大的优先级；

⑤ ift%D==0

⑥ 样本特征提取，构造如式(14)所示的特征矩阵X；

⑧ 偏差模型求解，将偏差模型参数更新为w=(XTX)-1XTy；

⑨ end if

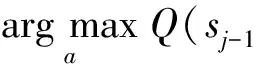
Q(Sj-1,Aj-1)；

其中行⑤～⑨是偏差模型更新的过程，需在t,t+D,t+2D,…等时间步计算经验池的样本特征和优先级偏差进行训练，求解模型参数w.行⑩是优先级校正的过程，通过偏差模型得到样本真实优先级的估计.行在优先级的基础上加入随机性，样本被采样的概率与优先级成正比，同时所有样本都有机会被采样.行～计算损失函数的梯度，计算梯度时需在TD-error的基础上乘以重要性权重(importance sampling weight)系数[42]，原因是按照优先级采样与均匀采样相比会给梯度的计算带来误差，因此使用采样概率的比值φ进行补偿[11]，并使用全部样本的φ的最大值进行规约，如式(20)所示.

φj=(N×P(j))-β,

(20)

其中,k=1,2,…,N,N为经验池容量，β是一个常数，P(j)为样本e(j)的采样优先级在全体样本中所占的比例，如式(21)所示.

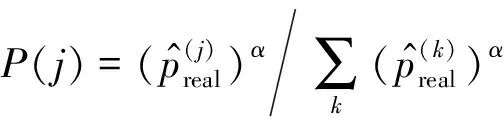
(21)

2.3.2 复杂度分析

ATDC-PER算法包括偏差模型和优先级校正两部分.根据分段更新策略，在执行D次优先级校正的同时会执行一次偏差模型更新.由于偏差模型更新的时间复杂度较高，而优先级校正仅执行矩阵乘法和加法，时间复杂度低，所以分段更新策略可以使复杂度高的部分以极低的频率执行，从而减少时间开销.

1) 偏差模型的复杂度分析.偏差模型更新包括样本特征提取、样本标签提取和模型求解3个阶段，分析如下：

① 样本特征提取.原始的样本特征维度为2，提取K阶多项式后的特征向量x(i)∈，特征矩阵X∈.其中，m的值不超过经验池总容量，且在经验池填充满之后不再变化，是一个常数.因此特征提取的时间复杂度和空间复杂度均为O(K2).

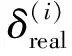
③ 偏差模型求解.模型求解阶段的时间消耗集中在式(17)中对参数向量w的求解上.XTX∈，在此基础上求逆的时间复杂度为Ο(K6)，空间复杂度为Ο(K2).

2) 优先级校正的复杂度分析.优先级校正阶段在提取样本特征Xt后与参数向量w执行矩阵乘法，时间复杂度为Ο(K4)，空间复杂度为Ο(K2).

由于ATDC-EPR算法中间隔D个时间步偏差模型才更新一次，D的取值较大，其余时间步都仅执行优先级校正的操作，因此总体时间复杂度为Ο(K4)，空间复杂度为Ο(K2).另外，一般K=2时偏差模型就可以很好地估计优先级偏差，此时求解参数w所需的逆矩阵(XTX)-1∈6×6，规模较小，可以快速求解.

经过复杂度分析，本文提出的ATDC-PER算法以极小的时间和空间代价就可以在Q网络每次迭代中校正经验池中样本的存储优先级，使用校正后的优先级选择样本.

3 实验结果与分析

本节首先介绍实验平台和环境，随后介绍ATDC-PER算法的参数选择，通过对比实验说明参数对性能的影响，最后从智能体的学习速度和最优策略的质量2方面对实验结果进行分析.

3.1 实验平台描述

实验使用基于Atari 2600游戏平台Arcade Learning Environment(ALE)[43]的OpenAI集成环境[44].ALE平台包含数十个视频游戏，并对外提供接口.ALE平台的挑战在于游戏种类和数量丰富，包含益智类、体育类、策略类、射击类、搏斗类等多种类型的游戏，需多个游戏中使用同一算法，在超参数固定的情况下，仅以原始屏幕图像作为输入进行学习和训练.

本文选择ALE平台中的19个游戏进行实验，游戏的简要介绍列于表1，各游戏界面如图10所示.可以看出，游戏类型多样，游戏的界面风格不同，在训练中Q网络的输入不同.同时，每个游戏中智能体需完成的任务不同，即最终学习的策略也不同.

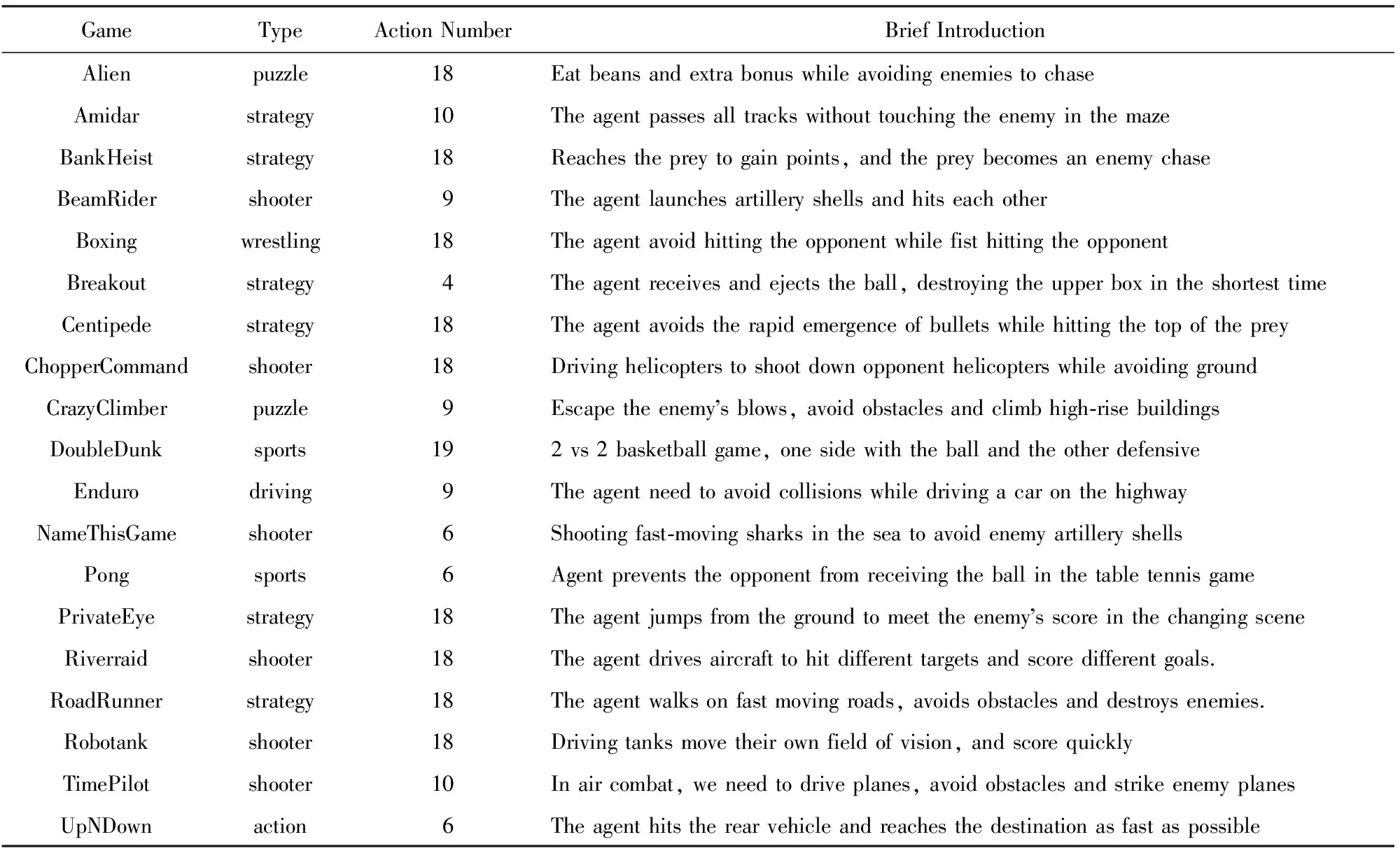
Table 1 A Brief Introduction to 19 Atari Games表1 19个Atari游戏的简要介绍

Fig. 10 State representations of 19 Atari games图10 19个Atari游戏的状态表示

本文使用的计算平台为戴尔PowerEdge T630塔式工作站，工作站配置2颗Intel Xeon E5-2609 CPU、4块NVIDIA GTX-1080Ti显卡(GPU)和64 GB内存，每个游戏使用单独的一块显卡进行训练.卷积神经网络基于Tensorflow[45]开源库实现，本文核心代码、实验结果和测试视频均可下载①http:pr-ai.hit.edu.cn20180510c1049a207703page.htm.

3.2 ATDC-PER参数选择

ATDC-PER算法在全部游戏中使用相同的超参数集合，以验证模型的通用性.ATDC-PER算法在PER算法的基础上增加了2个超参数，分别是偏差模型更新周期D和偏差模型特征阶数K，其余参数的设置与PER算法的设置相同.状态表示为原始图像预处理并叠加4帧组成的84×84×4的矩阵；Q网络为3层卷积神经网络，输出每个动作的值函数，目标Q网络的更新频率设为40 000；鉴于不同游戏的分值计算方式不同，使用符号函数对奖励进行规约；为了使训练更加稳定，对回传的梯度进行限制，使其不超过10.使用基于平方误差损失的Adam优化器进行训练，批量大小k=32，学习率设为10-4，折扣因子γ=0.99；探索因子在前400万帧从1.0线性递减至0.1，在随后的时间步内以之前速度的110线性递减至0.01后保持不变；经验池容量设为106；优先级计算中使用的参数α=0.6；重要性权重计算中使用的参数β初始值设为0.4，在训练中线性增加至1.0.

3.2.1 偏差模型更新周期

通过在Alien，Breakout，Pong的训练过程中使用不同的偏差模型更新周期D来测试参数D对Q网络学习的影响.在训练过程中的时刻t训练偏差模型得偏差模型参数wt，使用不同的参数D，测试模型wt在位于时刻t+D的经验池样本的平均损失，损失的计算如式(16)所示.不同的偏差模型更新周期D下的平均损失对比列如表2所示：

Table 2 Average Loss of Bias Model Trained in t Steps and Tested in t+D Steps Under Different D Values表2 比较不同D值下时刻t训练的偏差模型在时刻t+D测试的平均损失

由表2可知，随着偏差模型更新周期D的增加，损失总体升高.但从数值上看，损失的升高并不明显，特别是在105个时间步内，因此实验中将D的值设置为105.表2数据表明本文提出的偏差模型具有较强的泛化能力，对偏差模型更新周期D的选择不敏感，偏差模型可以在训练后较长的时间步内适用，同时也验证了图7所示的分段更新策略的合理性.

3.2.2 偏差模型特征阶数

偏差模型的特征阶数K越大，模型复杂度越高，训练误差越小，但计算复杂度也随之升高，同时可能引起过拟合.通过在游戏Alien，Breakout，Pong的训练过程中进行粗搜索来选择K的值.实验使用不同的K值进行训练，记录多个位于偏差模型更新周期中心的经验池样本，比较经验池样本的平均损失，结果列于表3.表3中数据表明，随着K值的增加，损失总体下降，但在K>2时损失的变化已经不显著，同时在Alien中K>3时有过拟合的趋势.因此，综合考虑损失和计算消耗，本文实验将多项式特征的阶数设为K=2.

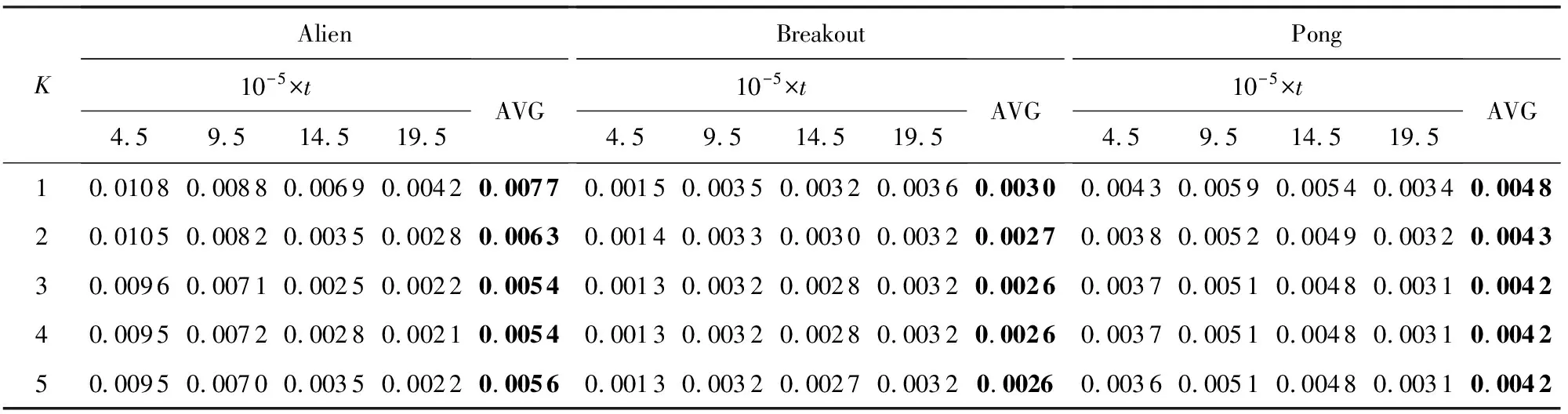
Table 3 Average Loss at the Center of Renewal Period of Correction Model Under Different K Values表3 比较不同K值下处于偏差模型更新周期中心的经验池平均损失

3.3 对比实验与分析

本文选择2个基线算法进行对比，分别为DDQN[27]和优先经验回放[11](PER).其中，DDQN算法中样本没有优先级，在训练时从经验池中随机取样；PER算法在DDQN的基础上为每个样本设置存储优先级，存储优先级与样本上次参与训练时的TD-error绝对值成正比，在采样时根据存储优先级依概率选择样本.本文通过偏差模型对存储优先级进行校正，用校正后的真实优先级的估计进行采样，提高了样本的利用效率.

算法的评价标准包括智能体的学习速度和智能体学习到的最优策略的质量.

3.3.1 智能体的学习速度

图11显示了19个Atari游戏的训练曲线，横轴代表时间步，每个时间步智能体与ALE环境交互一次，ALE环境会产生一帧新的图像.纵轴代表智能体在周期内获得的累计奖励.在训练开始后，随着迭代的进行，智能体的水平不断提高，奖励值不断增大，达到峰值后神经网络的训练可能趋于过拟合，因此训练后期奖励值可能会有波动.

ATDC-PER算法在19个游戏中的15个游戏收敛速度更快，能够以更少的交互次数达到最大奖励，如图11所示.特别是在Breakout，DoubleDunk，Enduro，Pong，Robotank，UpNDown这6个游戏中

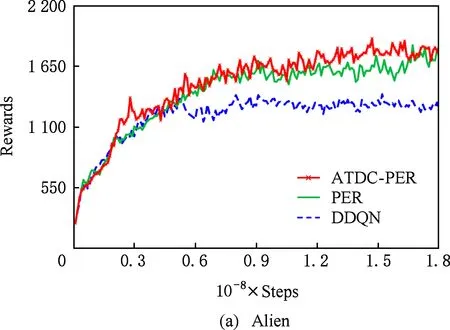
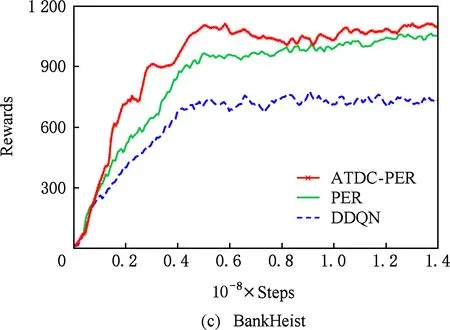
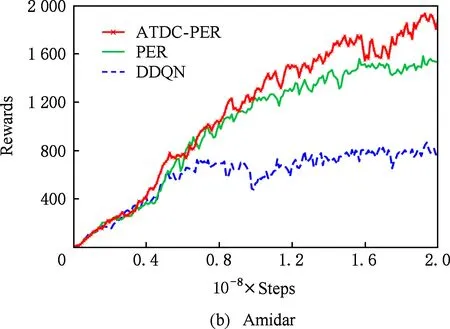
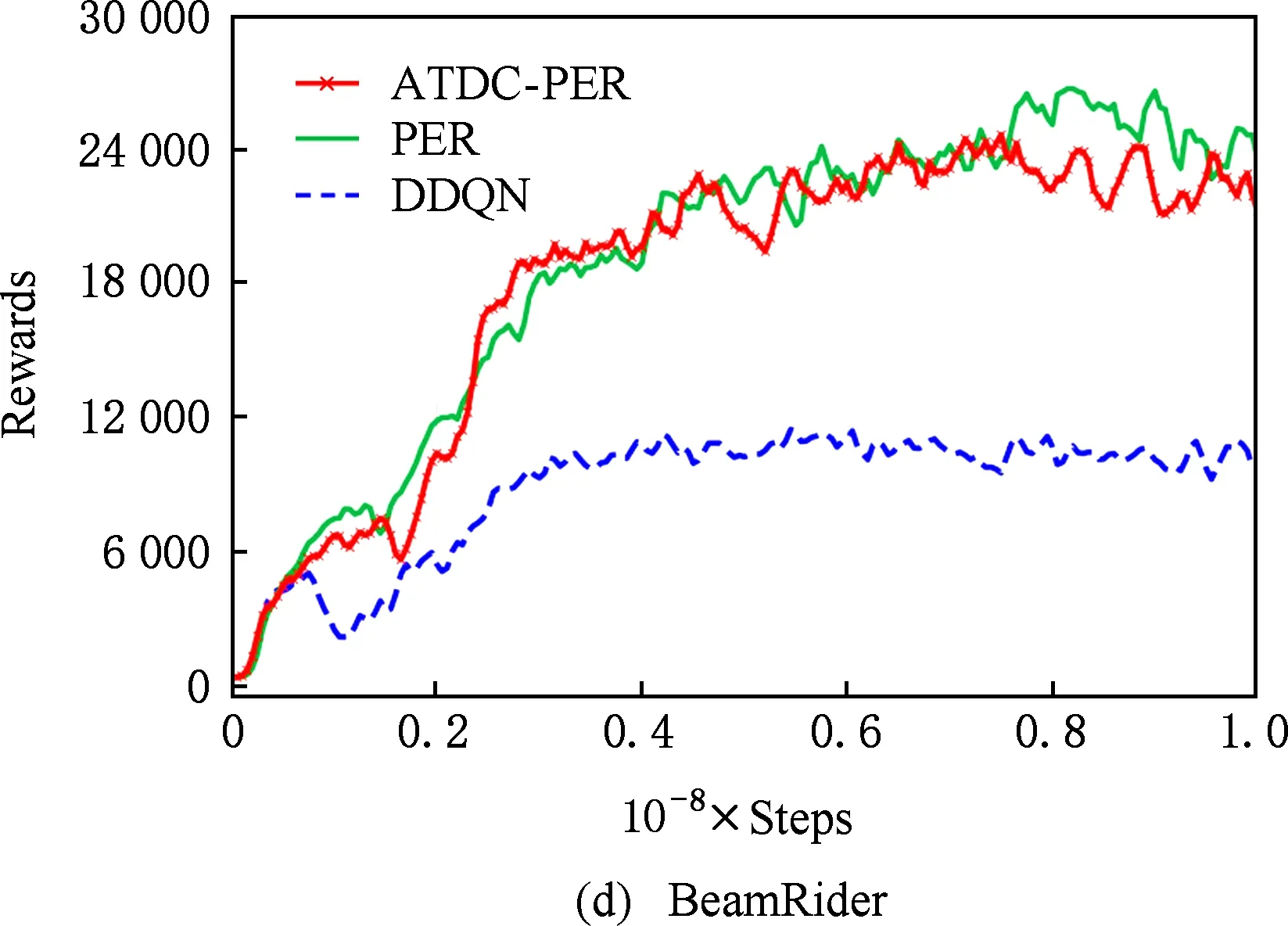
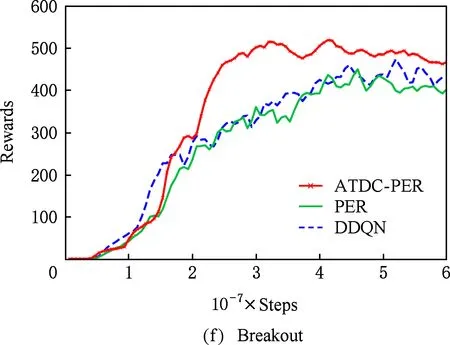
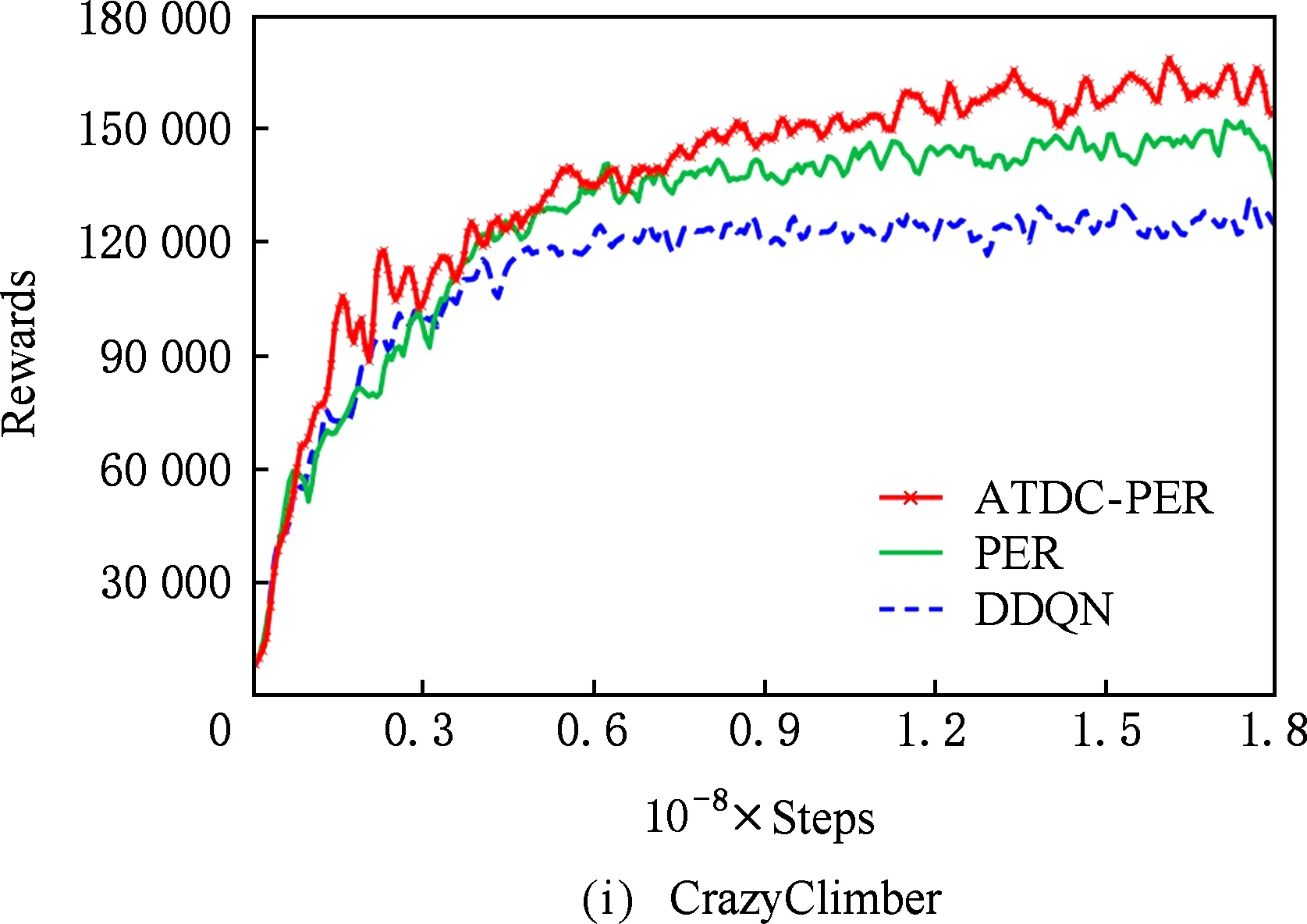
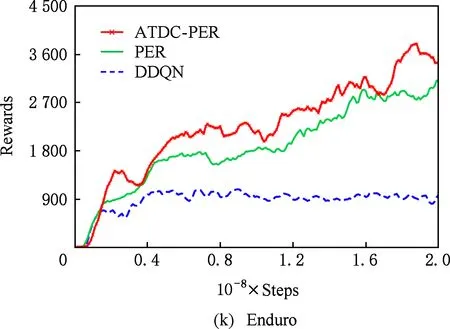
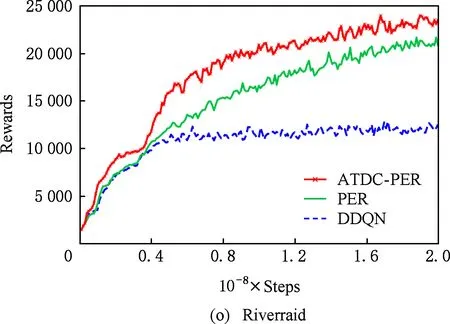
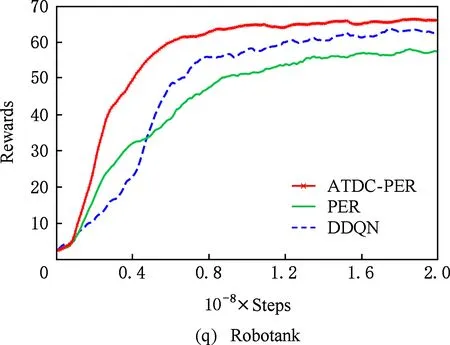
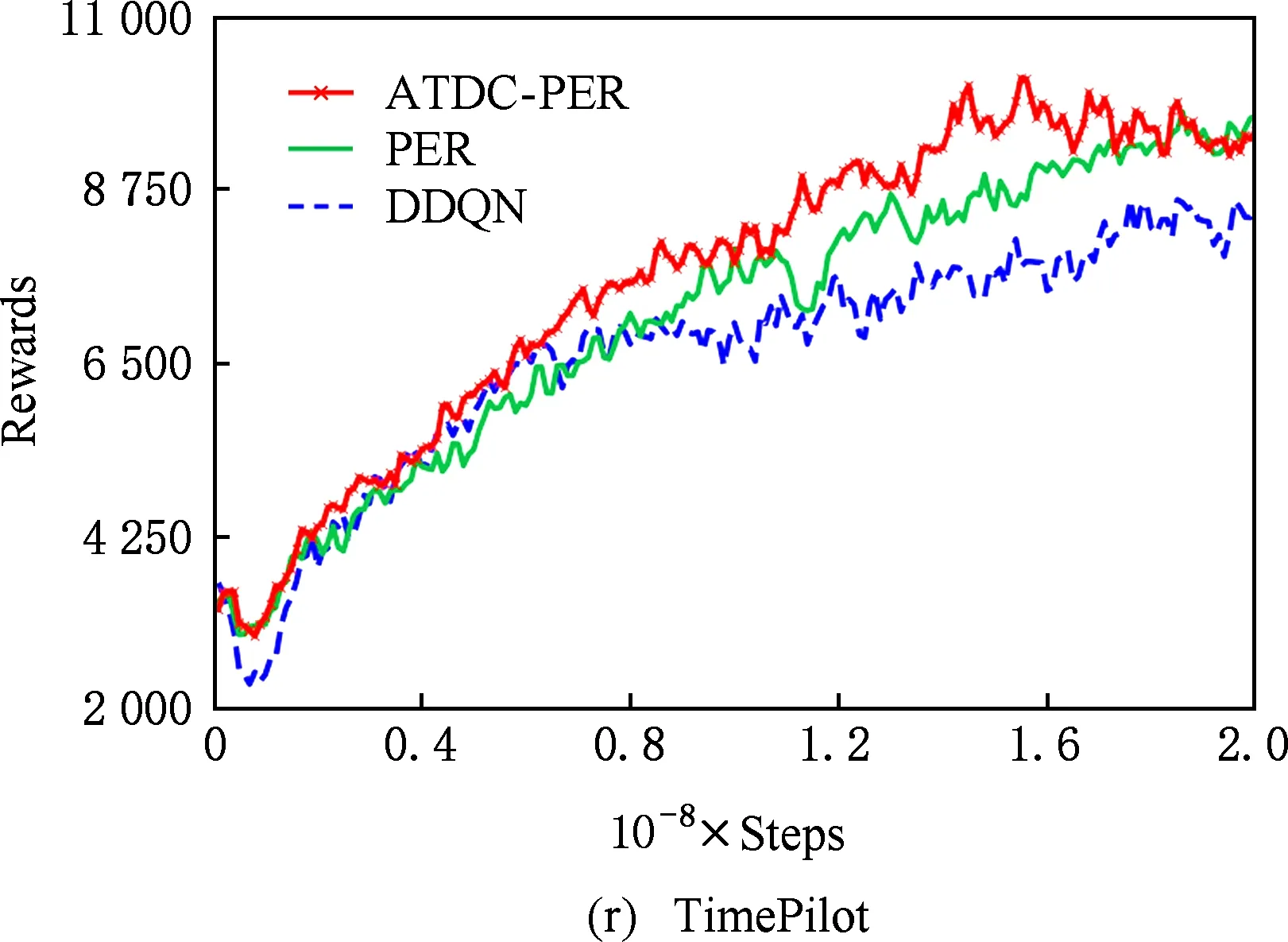
Fig. 11 Comparison of our method with PER [11] and DDQN [27] algorithms in training curve of 19 Atari games图11 本文方法在19个Atari游戏中与PER[11]和DDQN[27]算法的训练曲线对比

速度提升明显，分别如图11(f)(j)(k)(m)(q)(s)所示，在训练的相同时间步，ATDC-PER算法中智能体的得分水平总体优于DDQN和PER算法.图11中的曲线表明，本文提出的ATDC-PER算法通过在训练中校正经验池样本的存储优先级，提高了经验池样本的利用效率，提升了智能体的学习速度，减少了智能体与环境的交互次数，使智能体以更少的迭代步收敛.

3.3.2 最优策略的质量

最优策略反映智能体最终的学习结果，训练结束后使用最优策略可以指导智能体在ALE环境中获得良好表现.ATDC-PER算法中策略表示为Q网络参数，训练结束后智能体可以得到完整可复用的策略.训练过程中保存每个时间步所在周期的奖励值，同时每隔105个时间步保存一次Q网络参数，训练结束后选择奖励曲线平滑后处于峰值点的Q网络参数作为最优策略，通过测试最优策略的质量对学习效果进行评价.

最优策略的评价方法与DDQN[27]中相同，首先，周期开始时智能体与环境随机进行1～31次无动作交互，为测试提供随机的初始状态.随后，智能体按照最优策略的ε-贪心策略选择动作，探索因子为0.05.每个周期智能体与环境最多进行18 000个时间步的交互，策略的最终得分为100个测试周期得分的平均值.鉴于每个游戏的分值计算方式不同，使用式(22)在实际得分的基础上计算规约得分.

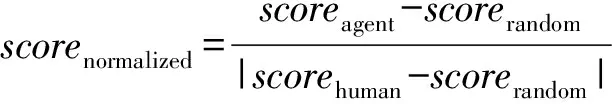
(22)

其中,scorerandom为随机智能体的得分，scorehuman为人类专家的得分，规约后的分值大于100%表明智能体的水平已经超过了人类专家水平.

19个Atari游戏总体的最优策略评价结果比较列于表4，单个游戏的评价结果列于表5.表5中随机智能体(random)、人类专家(human)和DDQN算法的得分来源于文献[27]，PER算法的得分来源于文献[11].

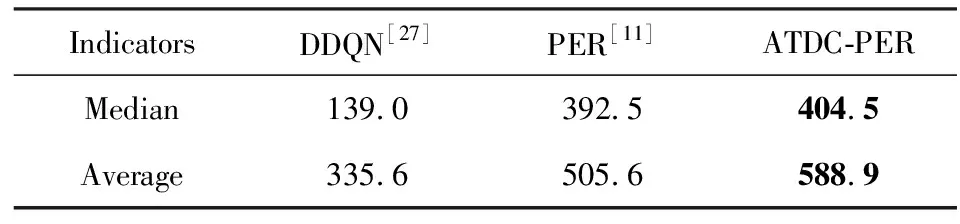
Table 4 Summary of Normalized Score on All Games 表4 全部游戏的规约得分评价表 %

Table 5 Raw Scores and Normalized Scores on All Games表5 全部游戏的实际得分和规约得分表

3.3.3 综合评价

表6显示了19个Atari游戏中智能体学习速度和最优策略质量的综合评价.结果表明，本文使用偏差模型校正后的真实优先级的估计来选择样本能够在训练中提升智能体的学习速度，同时提高最优策略的质量.本文算法在2种评价指标下都取得最好成绩的游戏达1419个，其中在1519个游戏中提升了智能体的学习速度，减少了智能体与环境的交互次数；在1519个游戏中改善了智能体的学习效果，提升了最优策略的质量.Boxing游戏比较简单，3种算法均能收敛到接近最大奖励值，本文算法和PER算法的收敛速度均略低于DDQN算法，但本文方法的最优策略得分优于其余2种算法，如图11(e)所示.BeamRider，NameThisGame这2个游戏不同方法的训练曲线交错上升，最后各算法达到的最优策略质量相似，均明显超过了人类专家水平.RoadRunner中本文方法的收敛速度优于DDQN和PER算法，最优策略得分略低于PER算法.PrivateEye游戏较难，3种算法的最优策略得分均不足人类专家得分的1%，均没有得到较好的结果.

Table 6 Comprehensive Evaluation on All Games表6 全部游戏的综合评价表

Note: ■ shows this method is the best among all of the comparison methods.

由表4和表5数据可知，ATDC-PER算法能够在全部19个游戏中的15个游戏获得更好的最优策略.最优策略规约得分的中位数相对于PER算法[11]提高12%，平均数提高83.3%.实验结果表明，本文方法通过提高经验池中样本的采样效率，可以改善智能体的最终学习效果，使智能体收敛到更好的最优策略.

4 结 论

深度Q学习中，基于优先经验回放的方法在训练中样本的存储优先级不能跟随Q网络迭代而更新，存储优先级不能准确反映经验池中样本TD-error分布的真实情况，从而降低了大量样本的利用效率.使用样本的真实优先级对经验池样本进行采样能够明显提高经验池样本的利用效率和学习的效果.

本文提出的基于TD-error自适应校正的主动采样方法，利用样本的回放周期和Q网络状态能够校正样本的优先级偏差，得到样本真实优先级的估计值，以极小的代价逼近真实优先级的分布.偏差模型在训练过程中分段更新，且对更新周期不敏感，偏差模型特征阶数较小时就可以很好地估计优先级偏差，分段更新策略显著降低了本文方法的计算复杂度.在Q网络迭代的每个时间步使用校正后的优先级进行采样，能够提升Q网络训练中经验池样本的利用效率.在Atari 2600中的实验结果表明，使用本文方法进行主动采样提升了智能体的学习速度，减少了智能体与环境的交互次数，同时改善了智能体的学习效果，提升了最优策略的质量.