列车制动盘试验测试与数值模拟的温度偏差分析*

2019-02-20

润滑与密封 2019年2期

(大连交通大学连续挤压教育部工程研究中心辽宁大连 116028)

盘形制动由于具有制动性能稳定、热承载能力强等特点[1-2]，被高速列车广泛采用。在盘形制动过程中，摩擦副常常处于高温、高应力状态下，尤其是在制动初速度高于200 km/h时，制动盘面临着更苛刻的温度和应力，这将直接影响到行车安全[3]。因此，认识制动盘的温度分布规律一直是这个领域许多学者关注的问题[4-8]。李继山等[9]、夏毅敏等[10]采用数值模拟的方法分别对高速动车组制动盘进行了温度场仿真分析，PANIER等[11]利用红外热像仪，在1∶1试验台上研究了制动盘表面热梯度。DEGALLAIX等[12]以1∶1试验台结合有限元计算的手段研究了制动盘失效机制，利用热电偶测试了摩擦副温度的变化情况。这些研究结果对于分析制动盘的温度分布、预测制动盘的使用寿命具有很大的参考价值。然而，由于这些研究所用的模拟计算条件、测试方法都各不相同，所得结果难以判定是否一致；同时，由于所采用的测试方法不同，这些测试结果之间究竟有多大偏差，也为人们正确认识制动过程中温度变化规律增加了困难。因此，对各种测试方法如红外热像仪、热电偶等得到的列车制动盘温度场，与模拟计算所得制动盘温度场进行对比，探讨各种方法之间差异，对于认识真实温度场的变化规律是非常有意义的。

本文作者通过1∶1列车制动试验台进行列车制动盘制动试验，利用红外热像仪、热电偶法测试了不同工况条件下的制动盘温度场的变化，并与数值模拟法计算结果进行比较，探讨了不同测试方法与数值模拟所得温度之间存在的误差及原因，以达到认识列车制动盘温度场变化规律的目的。

1 试验部分

制动试验的闸片材料为铜基粉末冶金材料，它是由10个三角形摩擦块镶嵌在制动钢背上组合而成(如图1所示)，其中单个摩擦块的面积为2 973 mm2，高度为20 mm，闸片总面积为29 730 mm2。制动盘外径和内径分别为640 mm和226 mm，平均摩擦半径为247 mm。

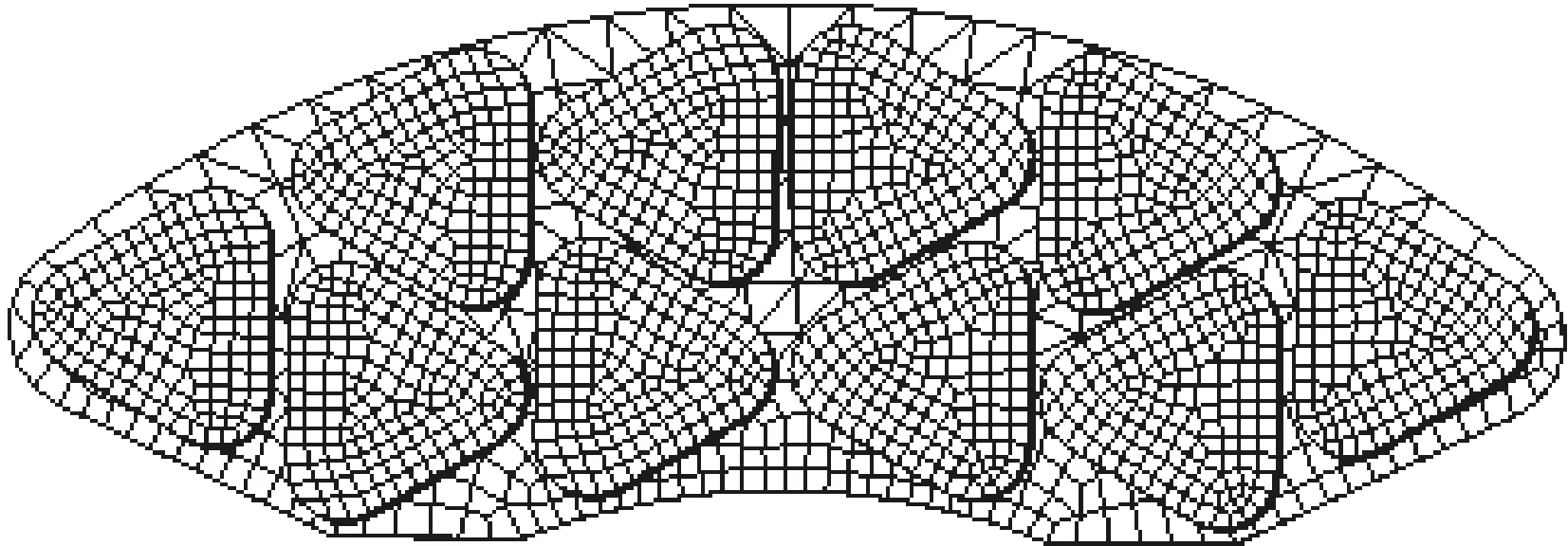
图1 制动闸片结构Fig 1 Brake pad structure

制动试验在1∶1试验台上进行，在进行制动试验前，在制动初速度120 km/h及闸片双侧压力32 kN的条件下，对闸片进行多次磨合，使闸片与制动盘的接触面积达到85%以上。磨合完成后，在干摩擦的条件下进行制动试验，选择制动初速度分别为80、120、160、200和250 km/h，闸片双侧压力分别为14、21.5、32 kN，转动惯量为1 129 kg·m2。

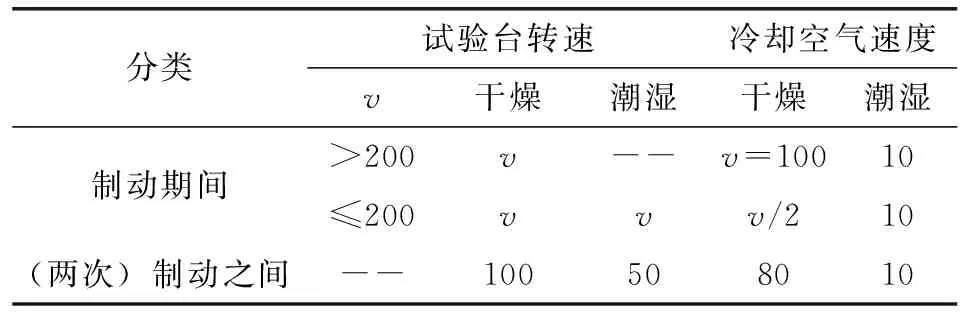
采用热电偶和PYROVIEW 640M红外热像仪2种方法测量制动盘盘面温度。热电偶在制动盘上的装配位置如图2所示，分别安装在每侧盘面盘半径的287、247、207 mm位置处，且距制动盘摩擦表面约4 mm。红外热像仪检测温度范围为200～700 ℃，发射率为0.84。试验过程中的试验台转速和通风条件如表1所示。

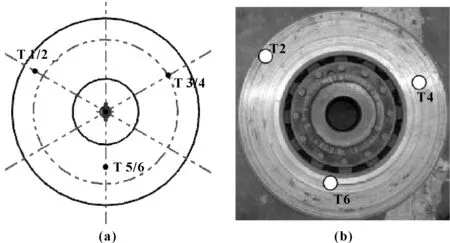
图2 热电偶在制动盘上的装配位置Fig 2 The assembly position of the thermocouple on the brake disc表1 1∶1试验台转速和通风条件Table 1 Speed and ventilation condition of 1∶1 test bench

km·h-1

2 数值模拟

采用ADINA有限元软件模拟制动过程中制动盘温度场的变化情况。考虑到盘体结构、热载荷的对称性，为节省时间和降低问题的复杂性，在模拟计算中，将摩擦副简化为实际模型的1/2，建立后的三维几何模型如图3所示。

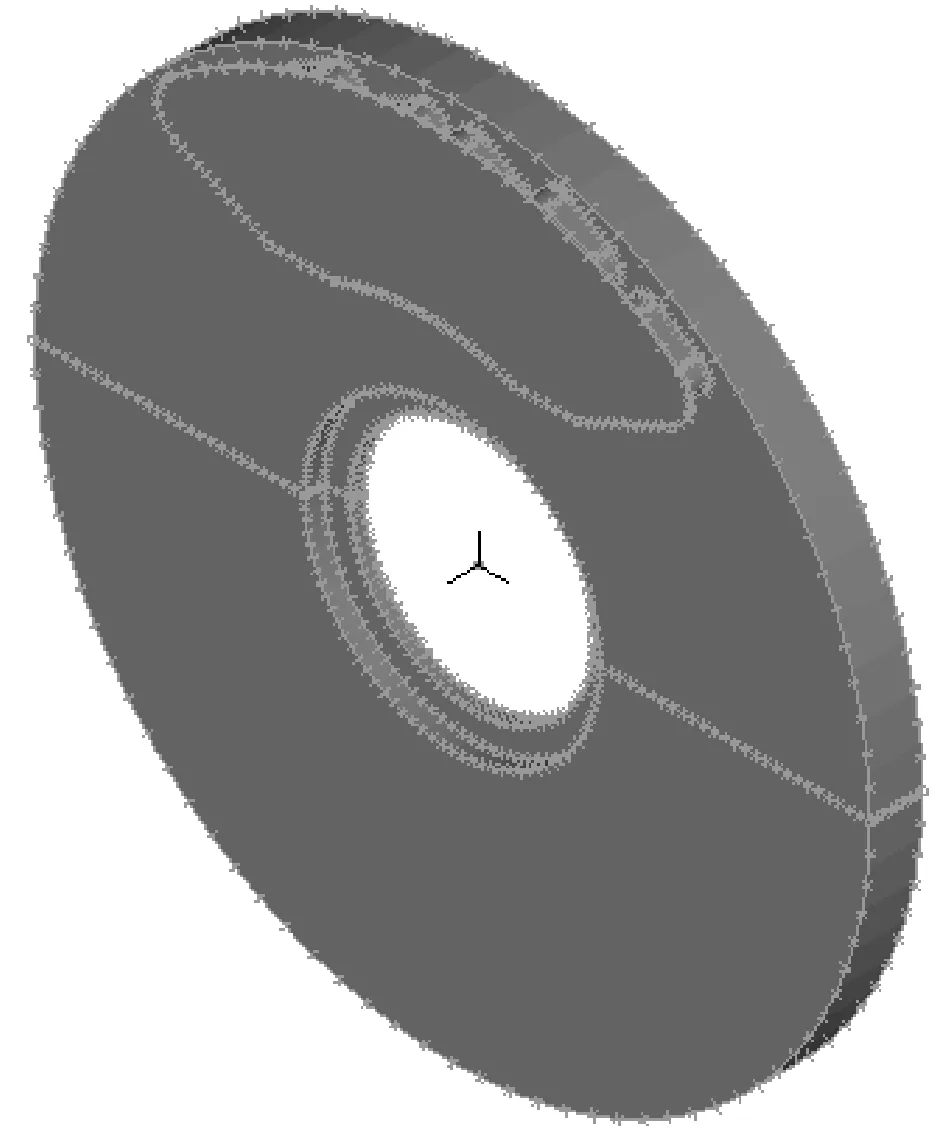
图3 列车摩擦副几何模型Fig 3 Geometric model of train friction pair

在进行有限元计算时做出如下假设：

(1)摩擦副之间为面面接触，忽略接触面之间的磨损；

(2)摩擦副表面粗糙度均匀，且摩擦过程中，材料的性能参数不随温度的变化而变化，摩擦因数恒定；

(3)制动压力均匀作用在制动钢背上；

(4)副擦副之间的散热方式为强制对流换热。

模拟过程中摩擦副与空气之间的强制对流换热关系式[13]如下：

(1)

(2)

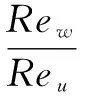
(3)

则对流换热系数为

(4)

模拟计算时设定的摩擦副材料性能参数如表2所示。

表2 摩擦副材料性能参数Table 2 Performance parameters of friction materials

3 结果分析与讨论

3.1 制动试验测试与模拟制动时间的对比

表3所示为单侧制动压力分别为10.75、7、16 kN时，不同制动初速度下试验测试和模拟的制动时间。可见：制动压力为10.75 kN，制动初速度为80 km/h的工况下，试验测试制动时间与模拟制动时间最为接近，两者的相差仅为0.4 s；制动压力为16 kN，制动初速度为250 km/h的工况下，两者制动时间相差最大，为19 s，相对偏差高达27.9%；同等压力下，试验制动时间大于数值模拟制动时间，且数值模拟制动时间与试验制动时间的差异会随着制动初速度的增大而增大。

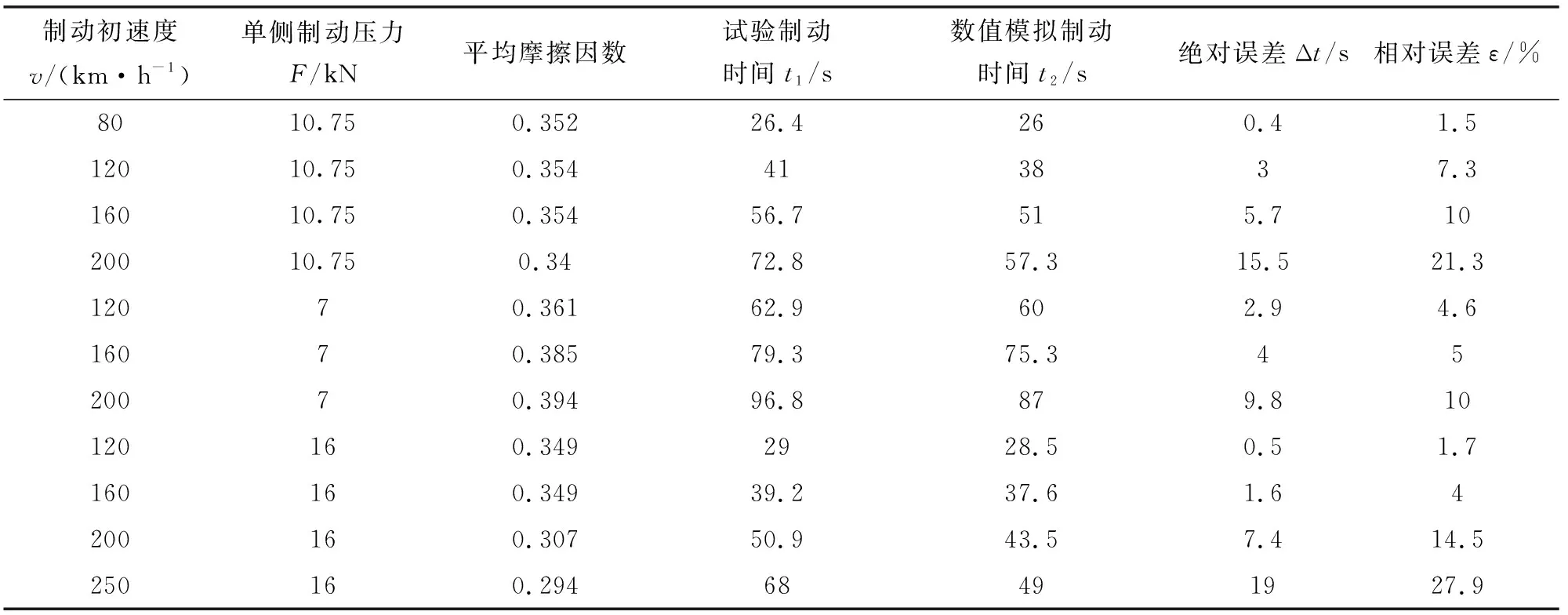
表3 不同工况下试验测试与模拟的制动时间Table 3 Braking time of test and simulation under different working conditions

试验制动时间大于数值模拟时间的原因可能是：试验过程中，闸片与制动盘为不完全接触(局部接触)，且闸片表面压力分布不均匀。两者制动时间差别随着制动初速度的增大而增大的原因可能是：随着制动初速度的提高，摩擦副产生的热能变大，制动盘表面的温度增加，在盘表面形成“第三体”数量增加，“第三体”的润滑作用导致摩擦因数在制动过程中波动较大，然而数值模拟计算中，设置摩擦因数是恒定的，导致两者之间偏离变大，从而导致了模拟计算与试验测试的制动时间的差异会随着制动初速度的增大而增大。

3.2 数值模拟与红外测试温度的对比

3.2.1 模拟计算与红外测试制动盘温度场变化情况的对比

由于数值模拟和试验制动时间并不完全相同，为了使数值模拟与试验测试的温度场具有可比性，选取数值模拟和试验中制动盘角速度相一致的时刻进行分析，换算关系如下：

(5)

式中:t试和t模分别为选取的某一时刻试验时间和相对应的模拟制动时间。t1和t2分别为试验测试制动总时间和模拟制动总时间。

图4所示为制动压力为10.75 kN，制动初速度为200 km/h工况条件下，不同时刻制动盘盘面温度场的数值模拟分布。从盘面的径向上看，在制动盘的不同半径处，盘面温度有所不同，径向上存在较大的温度梯度；从周向上来看，盘表面温度变化不明显。从制动过程来看，在制动初期，会在制动盘的外侧形成环状高温带，内侧带状高温带不明显；随着制动的进行，在制动时间为20 s时，摩擦区域内侧的高温带也明显出现，摩擦区域外侧的环状高温带温度越来越高；在制动时间到达31 s时，摩擦区域内侧高温带与盘外侧高温带融合，盘面达到峰值温度；在制动后期，环状高温区温度逐渐降低，并向整个制动盘边缘扩散，制动时间为72 s时，盘面温度分布较均匀。

图4 数值模拟的制动盘制动过程中盘面温度场变化(10.75 kN，200 km/h)Fig 4 The change of the temperature field of the disc surface during the braking process by numerical simulation(10.75 kN，200 km/h)

图5所示为在1∶1制动试验台上，单侧制动压力为10.75 kN，制动初速度为200 km/h工况条件下，试验测试的不同时刻制动盘盘面温度场分布情况。在制动初期(7 s)，制动盘摩擦区域的外侧出现狭窄的高温带，内侧高温带不明显；制动时间为20 s时，盘面温度进一步升高，两条高温带的径向宽度变宽，其中摩擦区域外侧高温带的温度达到了478 ℃，此时盘面温度最高；随着制动的进行，当制动时间为31 s时，处于摩擦区域外侧的高温区温度下降，而内侧高温区温度持续升高；制动时间达到45 s时，两条高温带温度基本一致并逐渐开始融合，此时摩擦区域温度开始均匀化；当制动时间为56 s时，摩擦区域温度降低，高温带逐渐消失；制动结束时(72 s)，整个盘面温度分布较均匀，径向、周向上基本没有温度梯度。

图6示出了数值模拟的盘面温度与试验测试的盘面温度的对比，图中给出同一种工况条件下2次重复试验的曲线及数值模拟曲线。可知：数值模拟与试验测得的制动过程中的温度场具有相类似的变化规律，在制动的前45 s内，制动盘表面径向温度曲线都呈“M型”分布，其中，模拟与试验测试的盘面波峰温度在7 s时偏差最大，为129 ℃；制动时间为20 s时，模拟与试验所得温度在波谷位置(盘半径250 mm处)偏差最大，为151 ℃，同时，试验测得的盘面波峰温度与波谷温度梯度最大，梯度值为12.7 ℃/mm，从而引起的热应力最大；制动时间为56 s到制动结束时，盘表面径向温度曲线由“M型”分布变化为“倒V型”分布。在制动前期(前20 s),数值模拟与试验测得的高温区(波峰位置)都位于盘半径的230和280 mm处(由摩擦块的排布方式可知，两波峰处摩擦接触弧长最长)，但在制动盘的径向方向上，数值模拟的温度梯度要比试验测得的温度梯度小得多；随着制动的进行，试验测得的第一个波峰位置由“1”变化到“2”，盘径向温度梯度变小；在制动中后期两者的温度逐渐趋于一致。

图5 红外测试的制动盘制动过程中盘面温度场变化(10.75 kN，200 km/h)Fig 5 The change of the temperature field of the disc surface during the braking process by infrared test (10.5 kN，200 km/h)

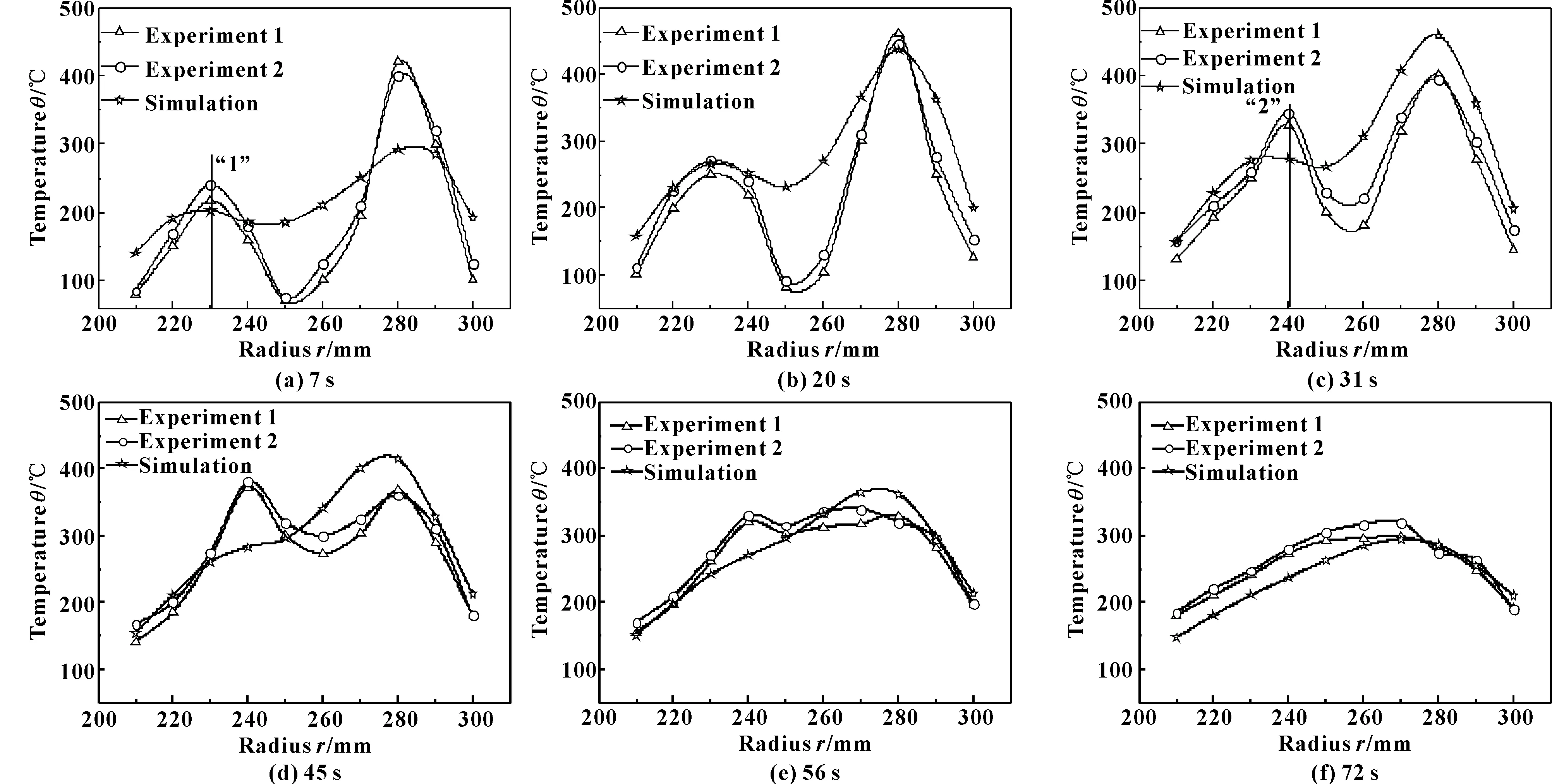
图6 数值模拟和红外测试的制动盘表面沿径向的温度分布 (10.75 kN，200 km/h)Fig 6 The radial temperature distribution of the brake disc surface by numerical simulation and infrared test(10.75 kN，200 km/h)

综上，在10.75 kN、200 km/h工况下，数值模拟与试验测得的温度值具有一定的差别，这可能与模拟条件的设定和实际试验过程中条件很难一致有关。在制动初期，摩擦制动中存在闸片与制动盘不均匀接触的现象，从而导致接触各点压力分布不均匀，局部摩擦生热不同，且由于制动时间较短，热传导不充分，所以制动盘径向温度梯度较大；而数值模拟过程中，摩擦副之间设定为面面接触，接触压力分布均匀，闸片与制动盘摩擦产生的热能取决于各点所在弧长和线速度，因此，盘表面径向温度梯度较试验测得的温度梯度小；随着制动的进行，试验过程中摩擦副之间材料发生磨损，闸片与制动盘贴合程度变好，接触状态与数值模拟中设定的趋于一致，同时在制动后期热传导占据主导地位，使得后期制动中两者径向温度变化曲线更加一致。因此，在试验测试过程中，当制动盘和闸片贴合较好的情况下，数值模拟与试验测试的温度场具有相同的变化趋势，这将为预测不同工况条件下，试验测试制动盘表面温度场的变化提供理论依据。

3.2.2 模拟计算与红外测试峰值温度的对比

图7所示为不同压力、速度下数值模拟和试验得到的制动盘峰值温度曲线，图中给出同一种工况条件下2次重复试验的曲线及数值模拟曲线。由图7(a)可见：在制动压力为7 kN时，数值模拟与试验测得的峰值温度曲线变化规律相同，都呈现出线性上升的趋势；在120和160 km/h的制动初速度下，2种方法所得的峰值温度基本相同，随着制动初速度的提高，在200 km/h时，试验测得的峰值温度比数值模拟所得温度高接近30 ℃。随着制动压力的增大，由图7(b)可得：在10.75 kN的制动压力下，模拟与试验测得的峰值温度之差进一步变大，试验峰值温度大于数值模拟温度，温度之差在50 ℃范围内。而由图7(c)可见：16 kN制动压力下，数值模拟和试验得到的制动盘表面峰值温度变化曲线与制动压力7、10.75 kN时的温度变化曲线并不一致，在制动初速度为160 km/h时，试验测试温度值高于模拟计算值210 ℃，但在速度为200 km/h时，两者又十分相近。造成这种差异的原因如图8所示，在试验过程中，由于之前连续做过多次制动试验，且最高温度在摩擦区外侧位置处形成(如图8(a)所示)，造成此处摩擦副磨损严重，接触开始不完全；随着制动试验的进行，在22 s时，摩擦副摩擦区外侧磨损进一步加剧，降低了这个区域的接触压力，而内侧接触压力增加，导致高温带位置向内侧偏移，盘面峰值温度下降(如图8(b)所示)。而在模拟计算中，忽略了摩擦副材料的磨损，造成了数值模拟与试验得到的温度相差较大。

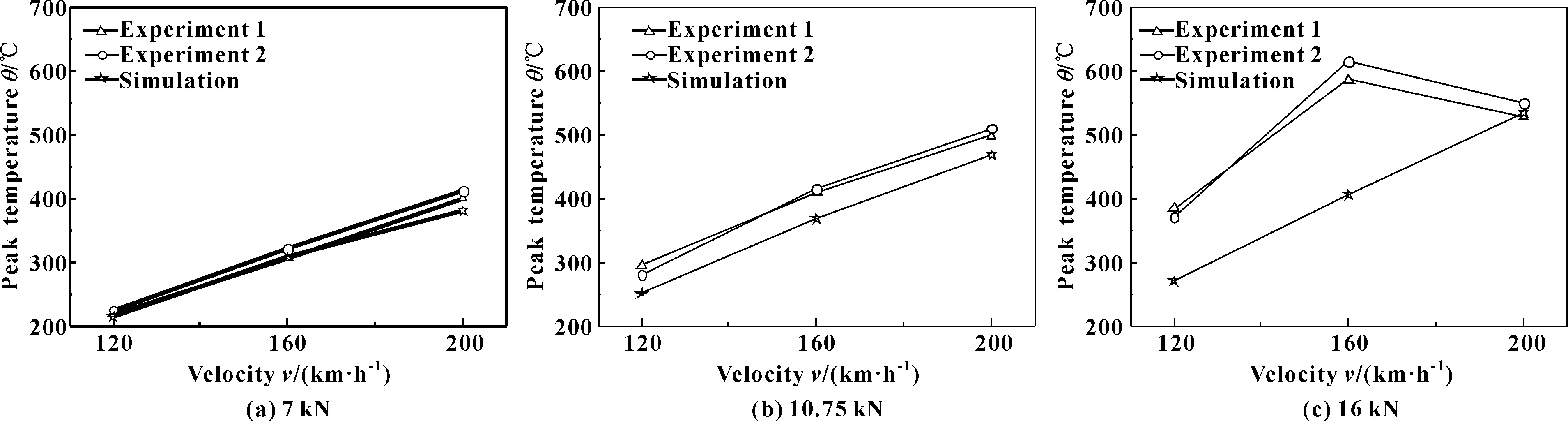
图7 数值模拟和红外测试的制动盘表面峰值温度Fig 7 The peak temperature of the brake disc surface by numerical simulation and infrared test

图8 红外测试的部分时刻制动盘盘面温度场分布(16 kN，200 km/h)Fig 8 Temperature distribution of disc surface by infrared test at part time(16 kN，200 km/h)

3.2.3 模拟计算与红外测试的盘面最大温度偏差

图9所示为不同工况下，红外测试温度相对于数值模拟盘面最大温度偏差情况。可见：在制动前期，红外测试温度相对于数值模拟温度偏差较大；如图9(a)所示，在制动初速度120 km/h、制动压力10.75 kN下的温度偏差最大，差值为89 ℃；随着制动初速度的提高，如图9(b)所示，在16 kN的制动压力下，制动减速到140 km/h时，试验与模拟温度偏差最大，偏差值为169 ℃；当制动初速度提高到200 km/h时，如图9(c)所示，在10.75 kN的制动压力下，减速到180 km/h时，红外测试与模拟温度偏差最大，差值为150 ℃。随着制动的进行，在制动中后期，2种方法所得盘面最大温度偏差变小，温度偏差控制在50 ℃范围内。造成前期温度偏差大的原因是：试验过程中盘面前期接触不充分，压力分布不均匀，盘面局部温度升高较快。

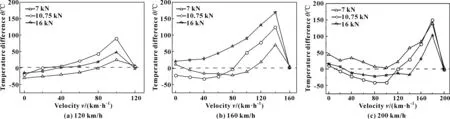
图9 红外测试与数值模拟的盘面最大温度偏差随制动速度的变化Fig 9 The change of the disc surface maximum temperature deviation between infrared test and numerical simulation with the braking speed

3.3 数值模拟与热电偶测试温度偏差3.3.1 模拟计算与热电偶测试盘面最大温度偏差

盘面布置6个热电偶，在制动过程中，选择其中的一个最大值与模拟计算得到最大值进行比较。图10所示为不同工况下，热电偶测试温度相对于数值模拟盘面最大温度偏差情况。由图10(a)、(b)可见：在120、160 km/h制动初速度下，从制动开始到制动结束，热电偶所测盘面温度都小于数值模拟温度；如图10(a)所示，在120 km/h制动初速度下，热电偶测试温度相对于数值模拟盘面温度偏差会随着制动压力的增大而增大，其中在16 kN的制动压力下，最大温度偏差可达到90 ℃；随着制动初速度的提高，如图10(c)所示，制动初速度由200 km/h减速到120 km/h时，在10.75 kN的制动压力下，温度偏差值最大，偏差值为232 ℃，在制动中后期，模拟计算温度开始小于试验热电偶所测温度。

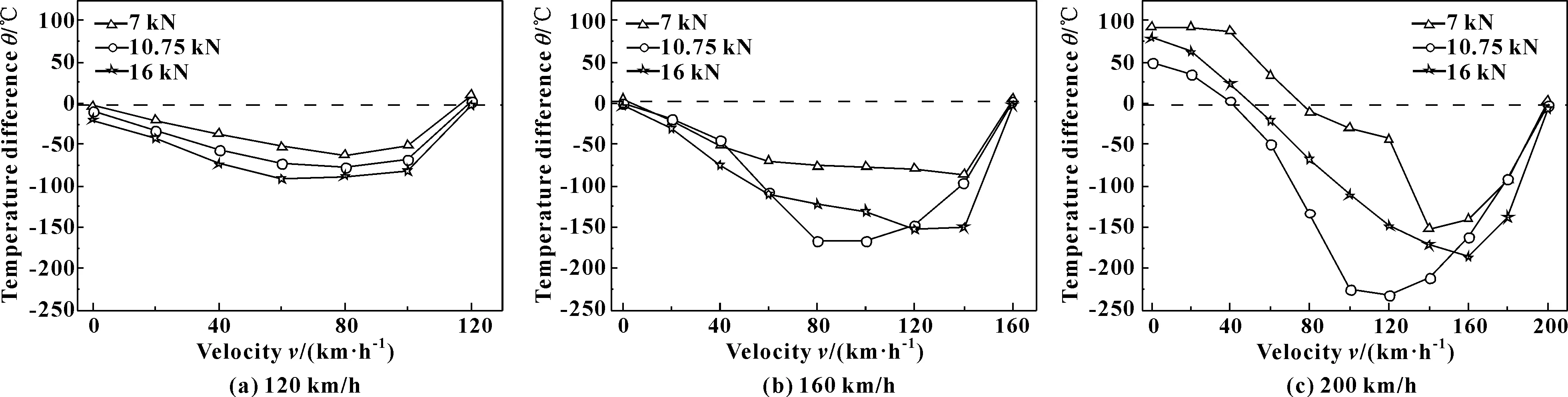
图10 热电偶测试与数值模拟的盘面最大温度偏差随制动速度的变化Fig 10 The change of the disc surface maximum temperature deviation between thermocouple test and numerical simulation with the braking speed

在试验制动前期，摩擦副有局部接触情况，局部温度升高较快，而6个热电偶位于制动盘上某一固定位置，并不一定为盘面最大温度处，因此，试验与计算温度偏差较大。随着制动的进行，摩擦副均匀接触程度增加，同时，在制动后期，热传导作用占据主导地位，此时热电偶所测温度更能反映盘面的整体温度，所以，在制动后期数值模拟温度与试验热电偶所测盘面温度偏差值逐渐变小。高速下(200 km/h)，在制动后期，模拟计算温度开始小于试验热电偶所测温度是由于随着制动初速度的增大，摩擦副之间摩擦生热变大，制动时间增加，热传导变好所致。

3.3.2 模拟计算与热电偶测试的盘面平均温度偏差

在制动过程中，选择6个热电偶所测盘面平均温度与模拟计算(热电偶的对应位置)得到盘面平均温度值进行比较。图11所示为不同工况下，试验热电偶相对于数值模拟盘面平均温度偏差情况。可见：数值模拟的盘面平均温度大于热电偶所测盘面平均温度，盘面平均温度偏差随制动速度的变化曲线呈“V”型分布；在制动过程中，2种方法所得盘面平均温度偏差随制动压力、制动初速度的增大而增大；如图11(a)所示，当制动初速度为120 km/h时，7、16 kN制动压力下的平均温度偏差最大值分别为55和83 ℃；如图11(c)所示，当制动初速度为200 km/h时，7、16 kN制动压力下的平均温度最大偏差分别为115和176 ℃；随着制动的进行，在制动后期，两者所得盘面平均温度偏差减小。

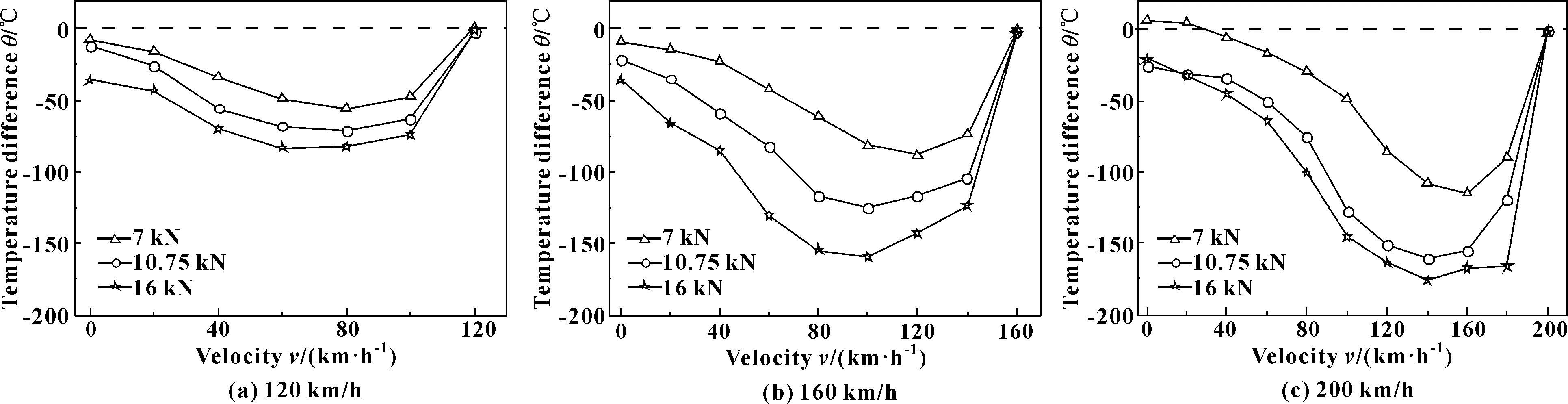
图11 热电偶测与数值模拟的盘面平均温度偏差随制动速度的变化Fig 11 The change of the disc surface average temperature deviation between thermocouple test and numerical simulation with the braking speed

综上，在制动过程中，红外热像仪所测得的不同工况下制动盘盘面温度与模拟所得温度最为接近，且随着制动的进行，在制动中后期，2种方法所得盘面温度偏差变小。