带回油线唇形密封的反向泵送机制研究与实验验证﹡

(1.清华大学摩擦学国家重点实验室 北京 100084;2.山东非金属材料研究所 山东济南 250031)

唇形密封(简称“油封”)是一种通过柔性唇口施加的径向力和唇口表面微观形貌的变形产生的反向泵送效应实现流体密封的接触式动密封，由于其结构简单、加工工艺成熟、安装方便等原因，广泛应用于各种机械旋转轴上[1-2]。随着现代工业的发展，对油封提出了在更高温度、压力和转速条件下保持优异性能的要求，为了应对严苛工况带来的技术挑战，人们在油封结构、材料等方面进行了大量研究[3]。回油线就是一种提升油封性能的优化结构，又称为回流线、回油沟、导流槽、流体动压油封等，通过在油封唇口及附近设计凸起结构以起到增强的反向泵送效果，是一种比较理想的耐压油封。

20世纪60年代，研究发现当油封唇口具有一定形状的花纹时，可以产生较强的流体动压效应，形成润滑油膜，从而延长了油封的使用寿命[4]。此后，人们开始了各种以流体动压效应为主的油封开发，包括波形油封、楔形油封、椭圆线油封等。1973年，BRINK和HORVE[5-6]通过实验证明了在空气侧增加回油线的设计可以提升油封的密封性能，并且推导出该工况下流体动压润滑的油膜公式，分析了不同因素对油封反向泵送率的影响。随着数值仿真方法的发展，近年来研究人员也开展了一些针对带回油线唇形密封的理论分析。LOPEZ等[7]利用有限元仿真得到油封唇口的静态接触压力分布，通过逆向求解二维雷诺方程，计算得到了不同条件下的反向泵送率。在此基础上，YANG 等[8-10]构建了三维有限元模型对流场进行仿真分析，研究了不同转速和回油线参数对油封密封性能的影响，得到的理论计算结果与实验测量取得了很好的一致性。国内尽管开发了各种形式的油封产品，但是针对回油线的设计缺乏系统的理论指导。现有的理论模型主要集中在固体仿真方面，且一般只分析了无压差下的情况，对于带回油线油封实际使用的有压差工况研究较少。

本文作者以某种带回油线的唇形密封作为研究对象，建立了考虑唇口变形和流体润滑耦合作用的三维有限元分析模型，并通过台架实验进行了验证。同时，基于该理论模型分析了油封在无压差与有压差条件下的密封性能和工作机制，可以为回油线的设计提供指导。

1 理论模型

图1为带回油线唇形密封的结构示意图。

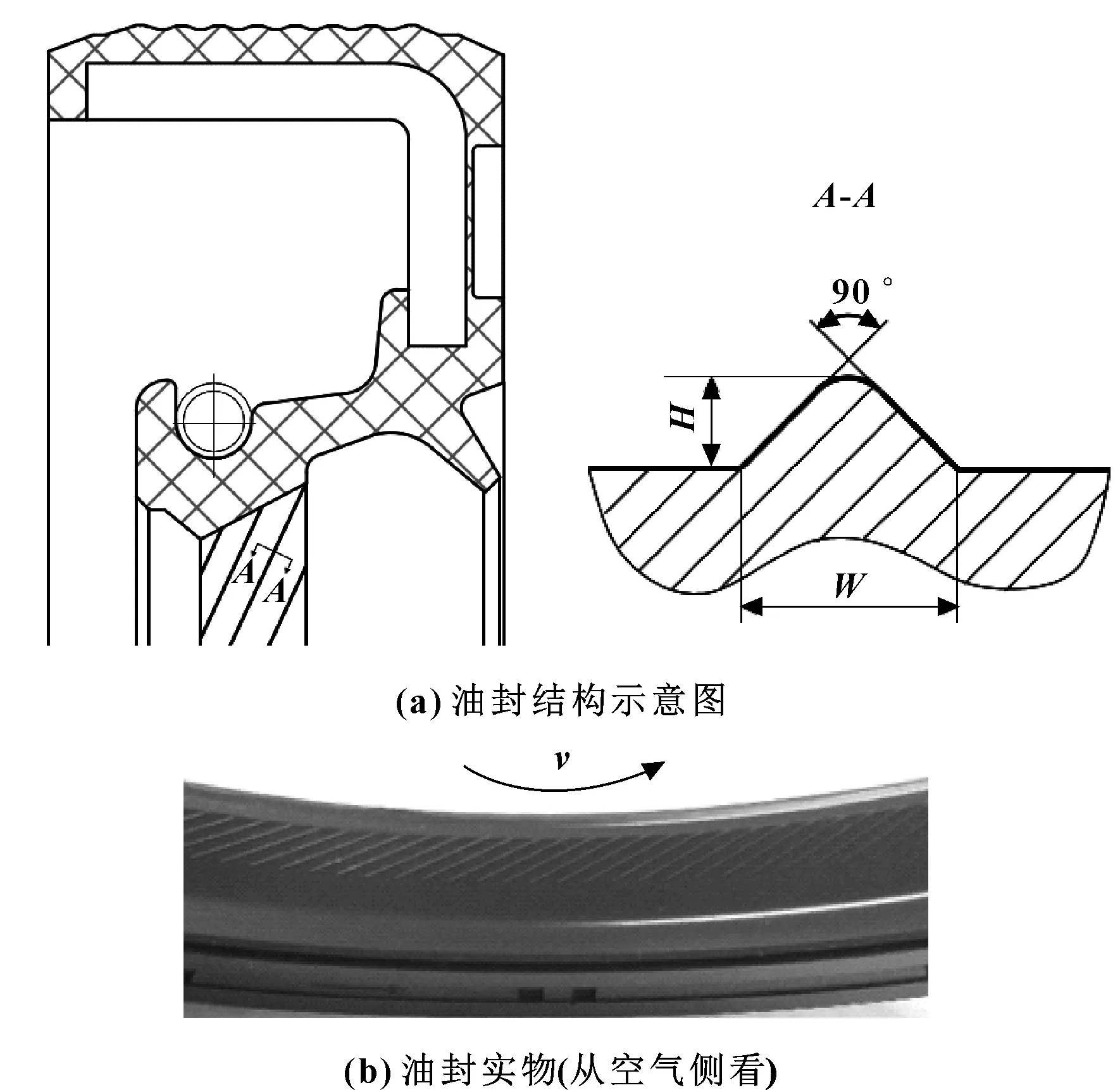
图1 带回油线唇形密封示意图Fig 1 Schematic diagram of lip seal with helix ribs(a)lip seal structure;(b)lip seal(from the air side)

油封材料为氟橡胶，回油线截面为等腰直角三角形，高度h=0.05 mm，宽度W=0.2 mm，使用轴径为115 mm。所用密封介质在40 ℃的密度为844.5 kg/m3，黏度为104 mm2/s。额定工况下密封介质压力为0.01 MPa，转速为3 000 r/min。理论模型包括固体力学分析、流体力学分析和流固耦合3个部分。

1.1 固体力学分析

固体力学分析的目的主要是为了获得油封的静态接触特性以及对应的流场模型。由于静态接触特性主要取决于油封材料和宏观结构，宏观结构中最关键的是唇口及附近区域，因此在固体力学分析中可以忽略回油线的微观结构，并且对唇口之外的部位进行简化以提高计算效率，包括忽略油封外圆柱面的沟槽、侧面的工艺槽等。简化后的油封结构、材料、约束和载荷都具有轴对称特征，可以直接采用二维轴对称模型进行分析。

网格划分选择轴对称四节点双线性单元，并根据不同区域的变形大小，对唇口和其他可能出现应力集中的部分进行网格细化处理，经过网格无关性验证，最终计算所用网格数目为39 701。

为了提高求解效率，各部件之间可能接触的位置均采用手动定义的面对面接触对。根据模型情况，选取了2种接触对类型：轴和油封唇口之间采用各向同性库仑摩擦模型；金属骨架和油封主体之间则采用绑定约束。

整个计算过程分为三步：第一步施加轴部过盈量；第二步在弹簧安装槽上施加弹簧力，这里为了便于处理，将弹簧力等效成作用在安装槽上的分布力进行施加[11]，弹簧力取10 N；第三步在密封腔一侧施加流体压力。最后计算得到不同工况下油封的接触压力分布曲线以及变形后的唇口轮廓，为流场分析提供基础。

1.2 流体力学分析

和静态接触特性不同，油封的流体力学特性主要受到回油线的影响，因此在流场分析的时候需要采用三维模型进行计算。由于文中涉及到的流场结构复杂，在保证计算效率和计算精度的前提下，参考相关文献和对比仿真验证，对流场结构进行如下简化：

(1) 假设空气侧充满流体，不考虑气液界面；

(2) 由于唇口附近的回油线是影响流场的主要因素，为了便于流场模型的构建，可以用唇口接触区靠空气侧区域的切面近似油封空气侧变形后的曲面；

(3) 油膜厚度远小于接触区的周向长度，因此可以忽略唇口的弧度变化，用平行表面近似油膜区；

(4) 由于唇口接触区处于流体动压润滑的状态，因此可以忽略唇口粗糙峰和油膜变形的影响，采用一维雷诺方程计算得到的最小油膜厚度表示接触区的平均油膜厚度[8]。

一维雷诺方程广泛应用于轴对称润滑模型，根据该方程，润滑间隙中的最小油膜厚度出现在空气侧的最大接触压力梯度处，计算公式如下：

式中：y是轴线方向；p是接触压力；v是轴表面转速；μ是润滑介质黏度。

对流场而言，尤其是不规则的复杂流场，网格划分对流动的模拟有非常大的影响，文中所涉及的流场就是典型的不规则复杂流场。为了保证计算精度，采用ANSYS ICEM软件进行结构化网格划分，以无压差工况为例，经过网格无关性验证后，最终计算采用的网格数目为189 716，不同工况模型的网格数目略有不同。

由于回油线是周期性设置在油封上，因此可以仅取一条回油线作为计算单元进行计算。流场外部分为三类边界，一是轴线方向分别设置压力入口和压力出口边界；二是周线方向，即在轴旋转方向设置周期性边界；三是径向方向，在上下表面分别设置墙边界。流场单元与边界设置如图2所示。

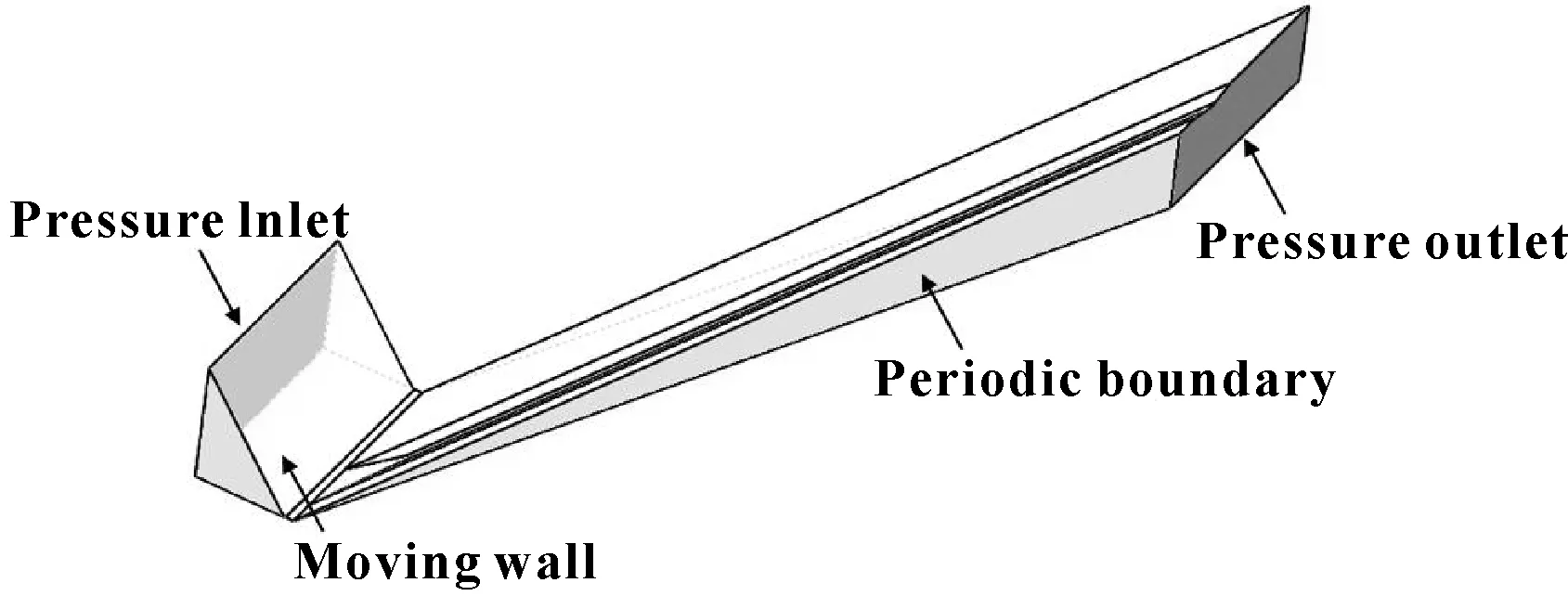
图2 流场模型与边界设置示意图Fig 2 Flow field finite element model and boundary setup

计算时设置监视平面，当监视平面的平均压力和流速达到稳定且进出口流量差与进口流量之比小于1%时认为计算结果已经收敛，每次计算大约耗时20 min。

1.3 流固耦合分析

由于分析对象使用的工作转速较高，为了使计算结果更为精确，需要对模型进行流固耦合分析。其思路是，首先通过固体力学分析获得变形后的唇口轮廓和接触压力分布，然后利用该轮廓构建流场模型，输入一维雷诺方程计算得到的最小油膜厚度作为初始膜厚，获得流场压力分布；之后再对油膜区域进行积分获得油膜对唇口的压力，与固体力学分析得到的唇口接触压力进行对比，调整油膜厚度及唇口轮廓，反复迭代计算，当有限元计算得到的油封唇口接触压力与油膜压力达到平衡时，认为已得到稳定的油膜厚度与流场分布；最后通过后处理获得反向泵送率和摩擦力矩等参数。

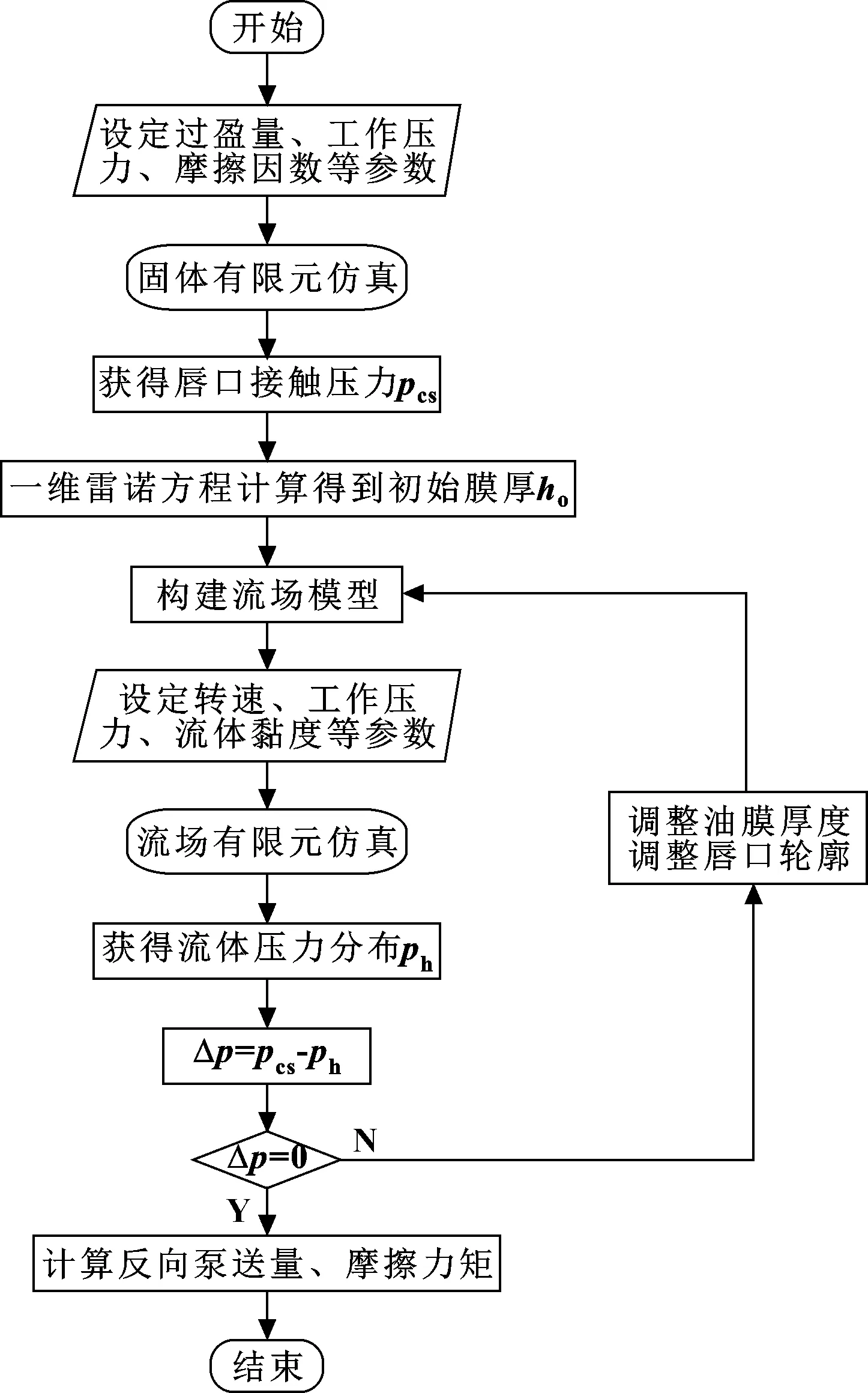
图3 计算流程图Fig 3 Calculation flowchart

2 实验验证

为了验证理论模型的正确性，首先进行了台架实验，实验装置如图4所示。

图4 实验设备Fig 4 Test rig

实验时将油封反向安装，每次测量前跑合15 min，使得泵送量达到稳定，在无压差情况下测量不同转速下的油封泄漏量，每个转速测量3次，取算术平均值作为该转速下的结果进行记录。图5所示为实验结果与仿真计算得到的反向泵送率的对比情况，可以看到，理论仿真与实验结果在较大转速范围内均具有很好的一致性，可以用于油封的优化设计和后续研究。

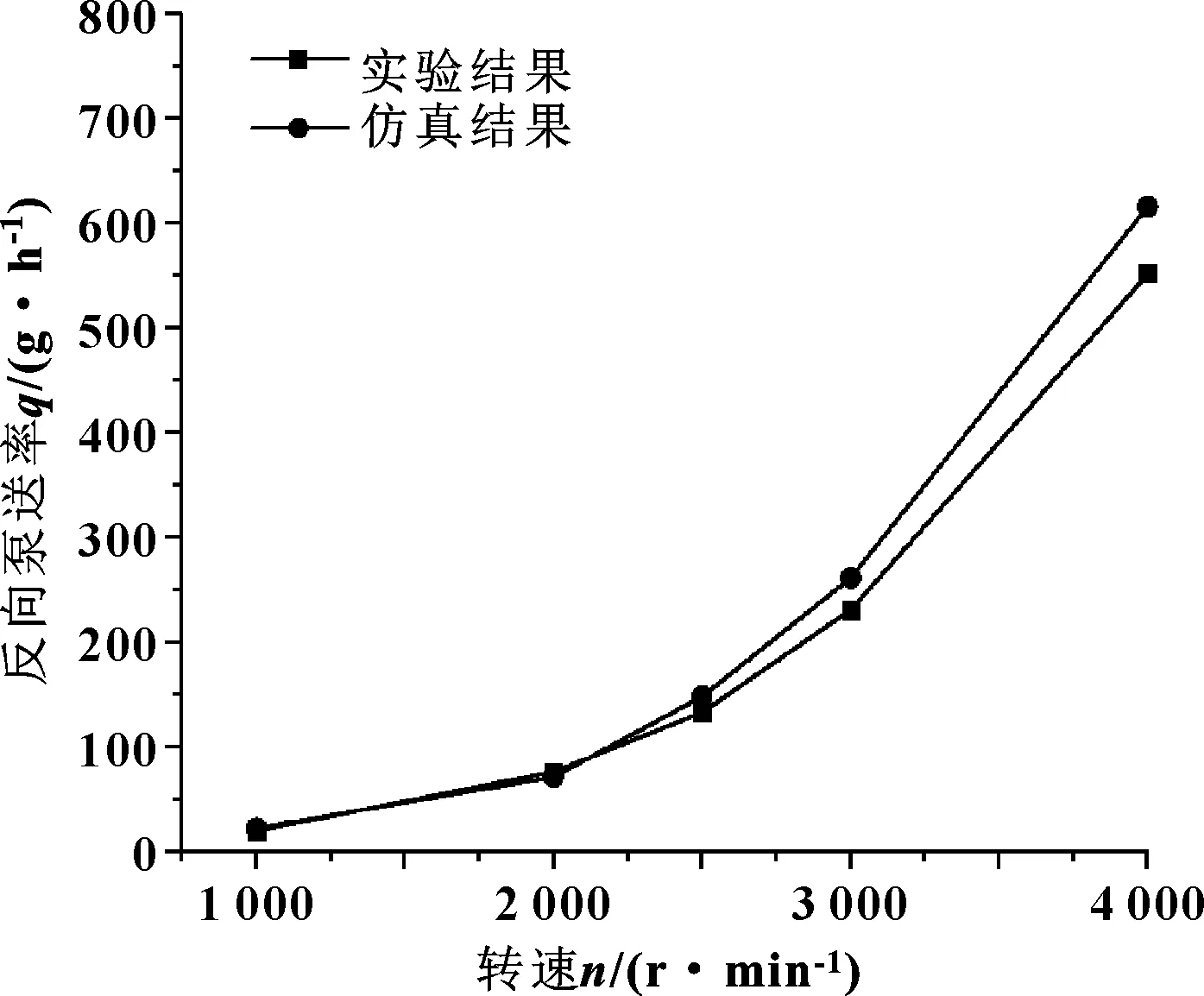
图5 无压差条件下实验与仿真结果对比Fig 5 Comparison of experimental results and simulation results under non-pressure condition

3 结果及分析

首先通过固体力学仿真，获得其静态接触特性和变形后的唇口轮廓。静态接触特性的分析参数选择接触压力分布，它除了保证静态密封之外，还会影响油膜的形成，进而影响动态密封效果。

图6示出了唇口的接触压力分布，其接触压力分布与普通油封类似，呈现较为明显的非对称性且压力峰值靠近油侧，压差作用下非对称性更为明显。实验测得无压差时的径向力为35.1 N，计算得到的径向力为33.5 N，两者误差小于5%，进一步验证了有限元模型的正确性。

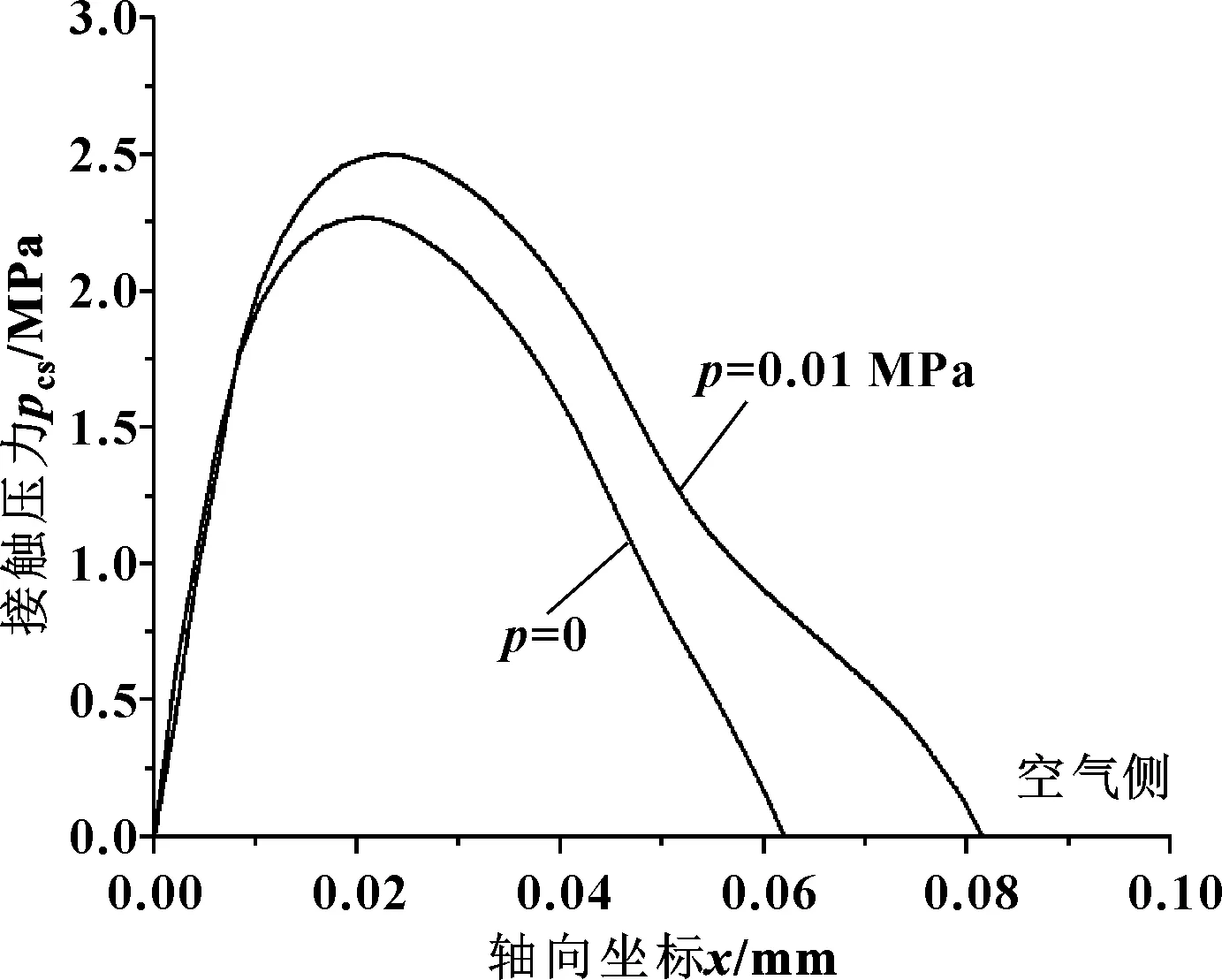
图6 唇口接触压力分布Fig 6 Contact pressure distribution of lips

图7(a)、(b)展示了无压差与有压差条件下轴表面的流场压力分布，可以看到有压力变化的区域均集中在唇口附近，且动压作用范围是唇口接触宽度的3～4倍。从局部放大可以看到，在轴旋转时，流体受到回油线的阻碍，在回油线的迎风面产生了高压区，背风面形成低压区，该压力分布有助于液体从高压侧往低压侧(即油侧)流动，从而实现反向泵送。

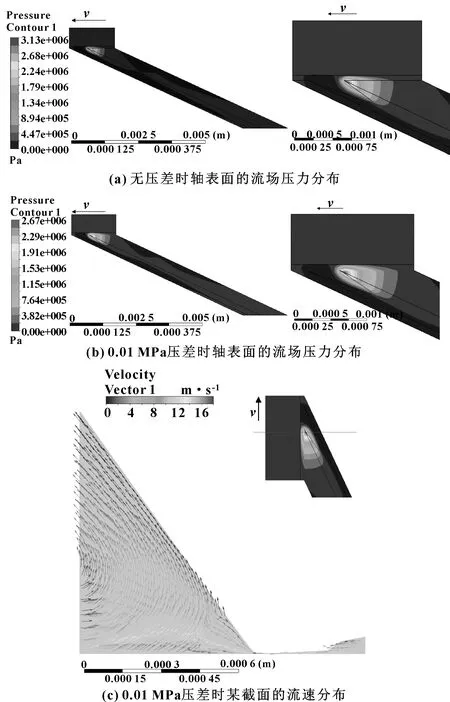
图7 流场仿真结果Fig 7 Flow filed simulation results(a) flow field pressure distribution on the shaft surface under non-pressure condition;(b) flow field pressure distribution on the shaft surface under 0.01 MPa;(c)velocity distribution of a section under 0.01 MPa

以额定工况为例，选取图中右上角截面观察流速分布，如图7(c)所示，可以明显看到，即使有0.01 MPa的压差驱动，液体仍然是从空气侧向油侧流动的。

通过对流速进行积分，可以获得各个边界的流量，出口流量即为反向泵送率，可以直接用于比较不同油封密封性能的优劣。文中算例计算得到的反向泵送率为407.5 g/h，相比普通油封大了1～2个量级。

此外，油封在工作时对轴产生的摩擦力矩也是评价油封性能的指标之一，它反映了油封的磨损程度，进而决定了油封使用寿命的长短。通过将轴表面的流体层中的剪应力沿整个唇口接触范围进行积分，即可求得油封对轴的摩擦力，再乘以回转轴的半径，即可获得摩擦力矩。文中算例计算得到的摩擦力矩为2.42 N·m，在正常范围内。

为了进一步分析该工况下的密封机制，将泵送量分解为两大部分：一是转轴速度作用下由回油线和密封结构的楔形间隙产生的流体动压效果引起的空气侧向油侧的泵送；二是由于0.01 MPa压差作用产生的油侧向空气侧的泄漏。单独对该模型设置压力和速度边界条件进行计算，分别得到2种条件下的流场压力和速度分布情况，如图8所示。可以看到，只有压差驱动的情况下，流体从油侧流向空气侧，唇口接触区产生压力降，回油线几乎不起作用，此时计算得到的泄漏量为7.7 g/h。仅有速度驱动的情况下，回油线发挥作用，整个流场的压力分布和图7(b)所示的结果非常相似，此时得到的反向泵送率为414 g/h。综合2个因素计算得到的反向泵送率为407.5 g/h，与分解计算得到的值406.3 g/h相比，差异小于1%，这也进一步验证了前面的分析。

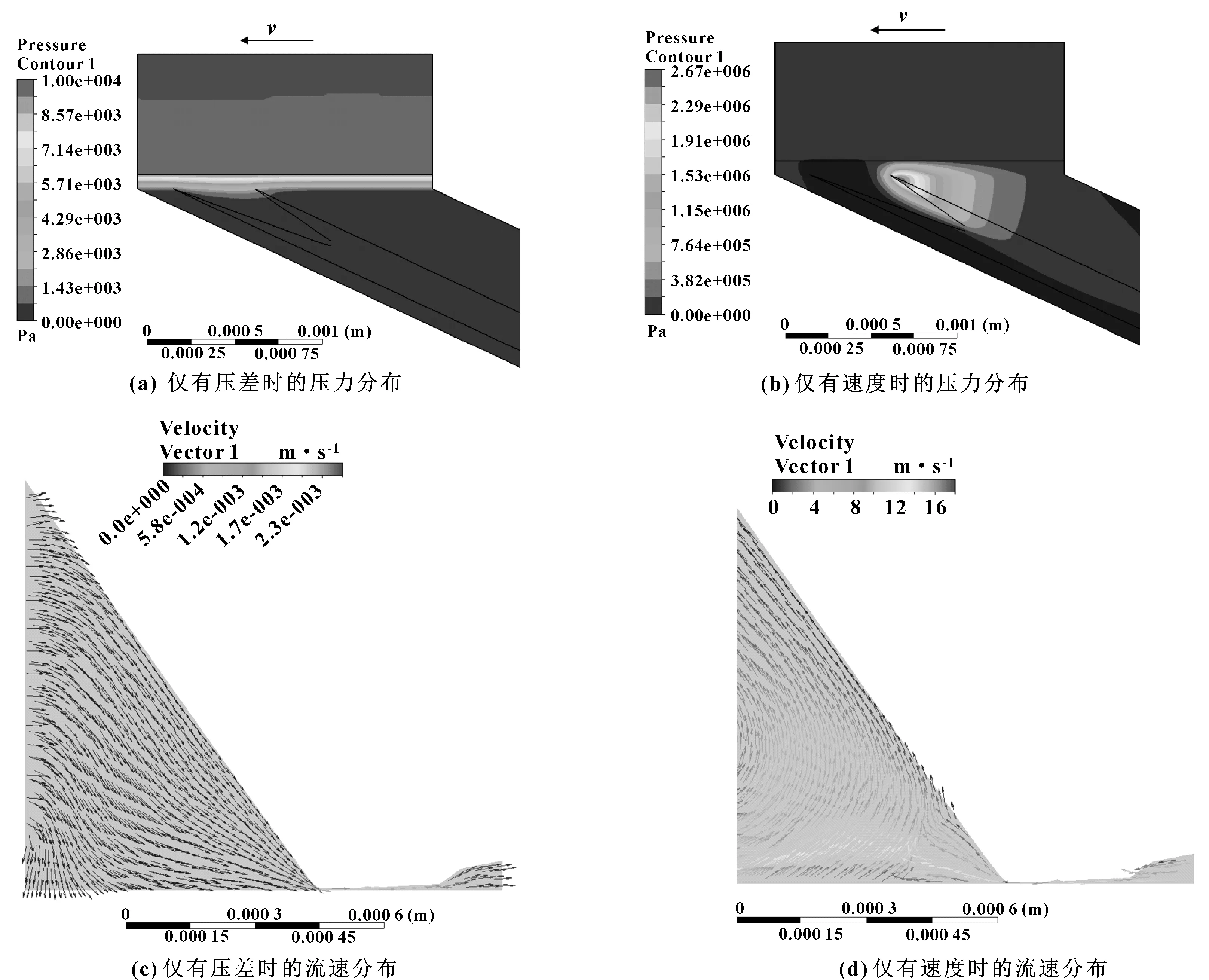
图8 0.01 MPa压差条件下的计算结果分解Fig 8 Decomposition of flow filed under 0.01 MPa(a) pressure distribution under pressure difference only;(b)pressure distribution when the shaft rotates only;(c)velocity distribution under pressure difference only;(d)velocity distribution when the shaft rotates only

4 结论

(1)带回油线唇形密封的静态接触特性与普通油封类似，唇口区域的接触压力分布呈明显的非对称性，且压力峰值靠近油侧，随着压力增大，其非对称性也更加明显。

(2)回油线的作用主要体现在动态流场区域，轴转起来后，在回油线的迎风面产生了高压区，背风面产生低压区，这种压力分布有助于实现反向泵送，且泵送量比普通油封高出1～2个量级。

(3)有压差作用时，带回油线的唇形密封仍然可以获得很好的密封性能，这是因为在转轴速度作用下由回油线和密封结构的楔形间隙产生的流体动压效果抵消了由于压差作用产生的油侧向空气侧的泄漏，并且速度越大，回油线的作用越明显。

(4)文中给出的理论模型具有计算量少、在宽转速范围内均保持良好精度的优点，可以应用到其他流体动压油封产品的设计开发上，具有很好的工程实用价值。