追寻教育的幸福模样

吴娟

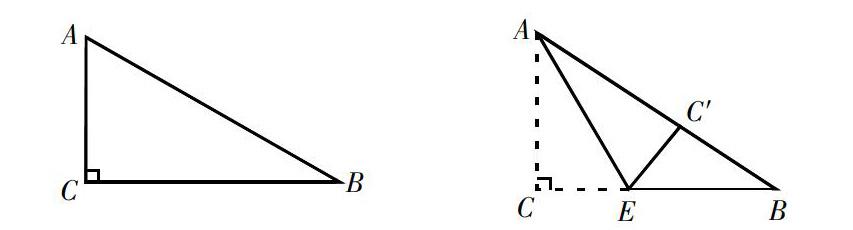
摘 要：随着基础教育课程改革的不断深入，人们越来越关注学生自主智慧解决问题的能力。近年来，本着“促进自主发展，成就幸福成长”的宗旨，着力打造培养学生的高阶思维的“幸福课堂”。探索构建从“了解”开始，力求“理解”深刻，关注“求解”重构，最终达成“见解”的有效生成——“四解课堂”模式。在四解课堂模式下“勾股定理在折叠问题中的应用”一课的教学设计。

关键词：教育;幸福;四解课堂

【学情了解】

学情了解是指教师有意识地设计问题，可以是学生复习旧知，可以是预习新知，促使学生去质疑问难。这样可以更好地激发学生的学习兴趣和学习欲望，有助于打开学生的思维。我是这样设计的：

操作：如图，是直角三角形纸片ABC，其中∠C=90°，将该纸片沿着过点A的直线折叠（折痕为AE），使点C恰好落在斜边AB上的点C′处。

师：在图中画出折痕AE，标出点C′。

师：你能发现哪些结论？（全等、边等、角等、线段CC′被折痕所在直线垂直平分）

师：利用你们刚才的发现，如果AC=3，BC=4，你会求CE的

长吗？

师总结：这道题目中，我们采用的方法是：根据折叠的性质，利用勾股定理构造方程来求出线段的长。一般步骤为：设标找列。

【知识理解】

知识理解可选择典型例题引导学生，并对例题进行拓展，点、线、面相结合，以点串线，以线拓面，从抓点到串线再到拓面逐步展开。抓“点”，就是抓基本知识点，抓重点，找难点，解疑点。我是这样设计的：

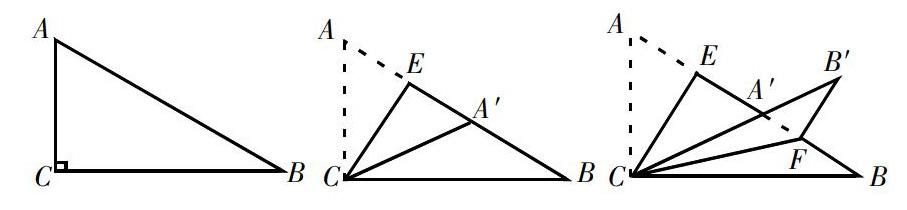
问题：如图，直角三角形纸片，∠C=90°，你会折出斜边上的高吗？

师：请某某同学展示下，为什么说折痕就是高？

师：在图中画出折痕AE，标出点C′。

师：如果AC=3，BC=4，那么高CE的长为多少？

師：此图中，还有哪些线段可以求出来？

生：AC′，AE，A′E，BE，AA′，A′B。

师：如果将三角形A′BC沿着过点C的直线折叠，使点B落在CA′的延长线上，你能画出折痕吗？先折一折，再画一画.

师：好，CB到哪里了？在这个图形里，你还能求出哪些线段的长？（精彩之处：45°的发现，B′F的长）

总结：我们在一次折叠的基础上进行二次折叠，假如直接问你求B′F的长，比较困难。我们采用的方法是根据折叠条件求出相关线段，逐步分析，拉近与B′F的距离。另外，解决折叠问题遇到困难时，我们还可以通过动手操作、观察来帮助分析。

【问题求解】

问题求解主要是精编一两道题目，让学生巩固所学知识点与思想方法，形成技能。主要采取先板演后说思路的方式，充分发挥优等生的积极性和榜样性，从而带动所有同学的学习兴趣。

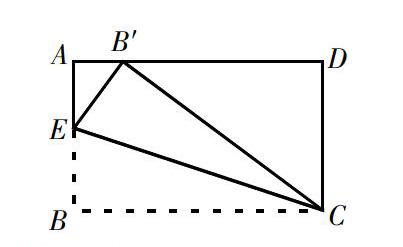
问题1.如图，长方形纸片（四个角都是直角，对边相等），其中AB=3，BC=5，将△BCE沿CE折叠，使点B落在AD边的B′处，求AE的长。

问题2.如图，将长方形纸片ABCD（四个角都是直角，对边相等）折叠，使点B与点D重合，折痕EF分别与AD、BC交于点E和点F，若AB=6，AD=8。

（1）证明：△CDF≌△A′DE;

（2）求△DEF的面积。

【我的见解】

我的见解是由学生通过自我认识、自主分析、反省评价，获得自我见解。学生之间先交流然后分享本节课的见解：折叠过程就是轴对称，折痕所在直线就是对称轴，我们采用的方法的一般是：设标找列等。教师进行综合与提炼，特别是思想方法的总结，从而使学生获得有效的见解，培养良好的思维品质，为终身学习核心素养奠定基础。

借助“四解模式”，上出一堂好课，追寻教育的幸福模样，从“自主导学”到“问题引领”再到“高阶思维”，一路走来，我们的课堂不断生长，不断超越，愿我们师生今后的课堂都能与这样的幸福和美好相伴而行！

编辑 杜元元