连点成线，学法自然

胡婉瑛

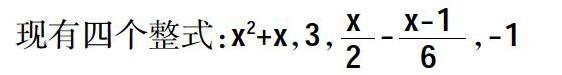
一、问题发现

复习是数学教学中的一个重要环节。上好一堂复习课，能够有效地帮助学生整合零散知识，吸收内化知识，熟练运用知识。然而，一次与学生偶然的沟通，让笔者对以往复习课的设计产生了质疑。在他们的印象中，数学复习课就是“知识点整理+习題讲解”。同时，他们也提出了自己的困惑：课上的习题都听得明白，课后去做类似的题目又没有头绪了。难道真的是学生的能力有问题？还是老师没有把题目讲透？或者根本就是复习课的“初衷”出现了问题，变成了纯粹的“习题堆砌课”？

二、现状分析

常见的数学复习课有以下三类。

第一类：“先理后练”型

先对一章节的知识点进行整理，再抛出一系列相关习题让学生训练。这样的课堂设计下，知识点梳理往往就变成了“走流程”，在学生的脑海中轻轻掠过，无法留下痕迹。后面设置的习题就像是一个个小碎片，学生捡起一块是一块。

第二类：“边理边练”型

一个知识点回顾完毕，搭配相关习题作为及时的巩固，然后继续下一个知识点，循环往复。这样的课堂通常能带给学生短暂的“成就感”，他们会以为自己掌握了。然而，此时学生的思维却被这一个个问题割裂开了。就好似“大珠小珠落玉盘”，亟须寻找那根串联的“线”。

第三类：“先练后理”型

一般以学生事先完成的一套单元综合试题作为课堂背景，在习题讲解中穿插知识点作为对本章节的复习。虽然通过训练，学生能够完成部分习题的解答，但是在他们的脑海中却无法搭建出整一章节的知识框架。问及这一章学习了什么，他们总是支支吾吾，说不清楚。

透视这三类数学复习课堂的根本问题，主要是教学内容的散点化和复习模式的碎片化造成学生思维过程的割裂化。

三、思想引导

《义务教育数学课程标准（2011年版）》指出：数学知识的教学，要注重知识的“生长点”与“延伸点”，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性。其核心思想是希望通过搭建整章或整本书的知识框架，联系新旧知识，让学生在不知不觉中掌握目标知识，获得思维过程的体验，从而进一步提升情感态度价值观。

由此，笔者有了新的思考：是否可以通过数学复习课堂的整体化设计，将学生脑海中一个个零散的知识点有效地连接起来，从而让学生自然地获得学习的“效能感”，以此激发他们的学习兴趣，进一步引发他们的数学思考。

四、教学实践

笔者以整体化教学为思维导向，针对章节与章节之间的“连线”以及习题与习题之间的“连线”对这两个复习课上的教学环节展开实践研究。

（一）章节之间的“连点成线”

案例背景：“一元一次方程”复习课中“概念复习”环节。

1.教学设计原稿

温故知新：

（1）什么是方程？

（2）什么是一元一次方程？

练一练：

下列各式中，哪一个是一元一次方程？（   ）

【师生活动】

1.请学生根据两个问题完成对方程和一元一次方程概念的复习。

2.以选择题形式的概念辨析作为即时巩固，请学生完成。个别回答时，请学生说出其他三个选项为什么不是一元一次方程。完成后，统计回答正确的人数。

【学习反馈】

对于两个基本概念的回顾，大部分学生无法第一时间给出完整的答案。思考后，仍有一部分学生支支吾吾，说不清楚。巩固练习的完成情况一般，尤其是具体问及其他三个选项不是一元一次方程的理由，学生表达情况参差不齐。

【成因分析】

作为复习课的一个重要环节，数学概念复习如果以直接抛出让学生回忆的方式进行，实践证明，效能很低。关键原因在于，会背不等于会用，能用了也不代表完全理解。对学生而言，原先的知识就像是散落在地的一块块碎片，那么有效的复习课就能帮助学生将这一个个碎片拾起、重构，在心中搭建出一个整体的框架。慢慢地，学生就会站在更高的位置上看待问题，解决问题。

2.教学设计修改稿

现请你选择其中两个整式用等号连接，并思考以下问题：

（1）共能组成______个方程。请你具体写出来;

（2）一元一次方程有哪些？请你写出来。

【师生活动】

（1）请学生回答第1小题。教师追问：为什么3=-1不是方程？

（回顾方程是含有未知数的等式）

（2）请学生回答第2小题。

（3）教师追问：为什么x2+x=3不是一元一次方程？

学生：因为这个方程中未知数的指数为2次。（投影：一元一次方程要求未知数的指数是一次）

教师进一步追问（投影展示）：好，既然要求是一次方程，那么我们将这个方程修改为：y+x=3，现在未知数的指数都是1次了，是一元一次方程吗？

学生：不是。因为方程中出现了两个未知数。（投影：一元一次方程要求只含有一个未知数）

教师再追问：那方程改为：+x=3，现在总该满足一元一次方程了吧？

学生：不是。因为一元一次方程要求等号两边都是整式。（投影：一元一次方程要求两边都是整式）

3.教师引导学生小结：我们通过自己列式、辨析，再一次深刻地回顾了什么是方程，什么是一元一次方程。（需要满足三个条件）

【学习反馈】

大部分学生非常快地写出了6个用等号连接的式子，并且通过问题有效地唤醒了脑海中关于方程的定义，排除了3=-1这个选项。同时，随着问题的层层递进，一元一次方程的定义也自然地出现在学生的口中。从学生的反应来看，问题设置的效果好，达到了复习相关概念的目的。

【设计意图】

（1）承前启后显整体

在问题的一开始设置了四个整式，作为与上一章“代数式”的连接，强化章节与章节之间的联系，凸显课程内容设置的整体性。如果学生也能够站在知识的整体性看待问题，那么这对于他们日后学习新的相关知识一定是具有指导意义的。

（2）环环相扣忆旧知

相比于传统的模式，教师直接给出一系列等式让学生来判断哪些是方程，哪些是一元一次方程，这样一种在探究中逐步得到方程、一元一次方程，并同步巩固一元一次方程的概念的方式，更能起到唤醒记忆，加深理解的作用。

（二）习题之间的“连点成线”

案例背景：“反比例函数中比例系数的几何意义”专题复习课中“模型应用”环节。

学生根据探究已经得到模型一（如图1）：S阴影=k1+k2

以下是在应用模型时对同样的两道习题的不同设计想法。

1.教学设计原稿

【师生活动】

（1）请学生依次完成习题1和习题2。

（2）教师适当引导，并根据学生的回答进行讲解。

【学习反馈】

根据模型，大部分学生能够较好地解决习题1，但在思考习题2的过程中，學生普遍反映没有解题思路，不知道怎么和模型联系起来。只有极个别学生给出了结果。

【成因分析】

习题1是对模型一的直接应用，图示明显，变化少。此题设置的本意就是作为模型即时巩固，让学生获得学习的效能感。而习题2是2015年宁波市中考填空题的压轴题，图示新颖，需要添加辅助线构造矩形或三角形，以此建立与模型之间的联系，学生不易想到，造成解题过程阻滞。

2.教学设计修改稿

【师生活动】

（1）请学生完成习题1，并请一位学生为大家讲述他的过程。

（2）教师在图2的基础上进行动画修改，为学生进行如下演示。

①根据反比例函数图象的对称性，分别画出两个图象的另一支曲线，如图4。

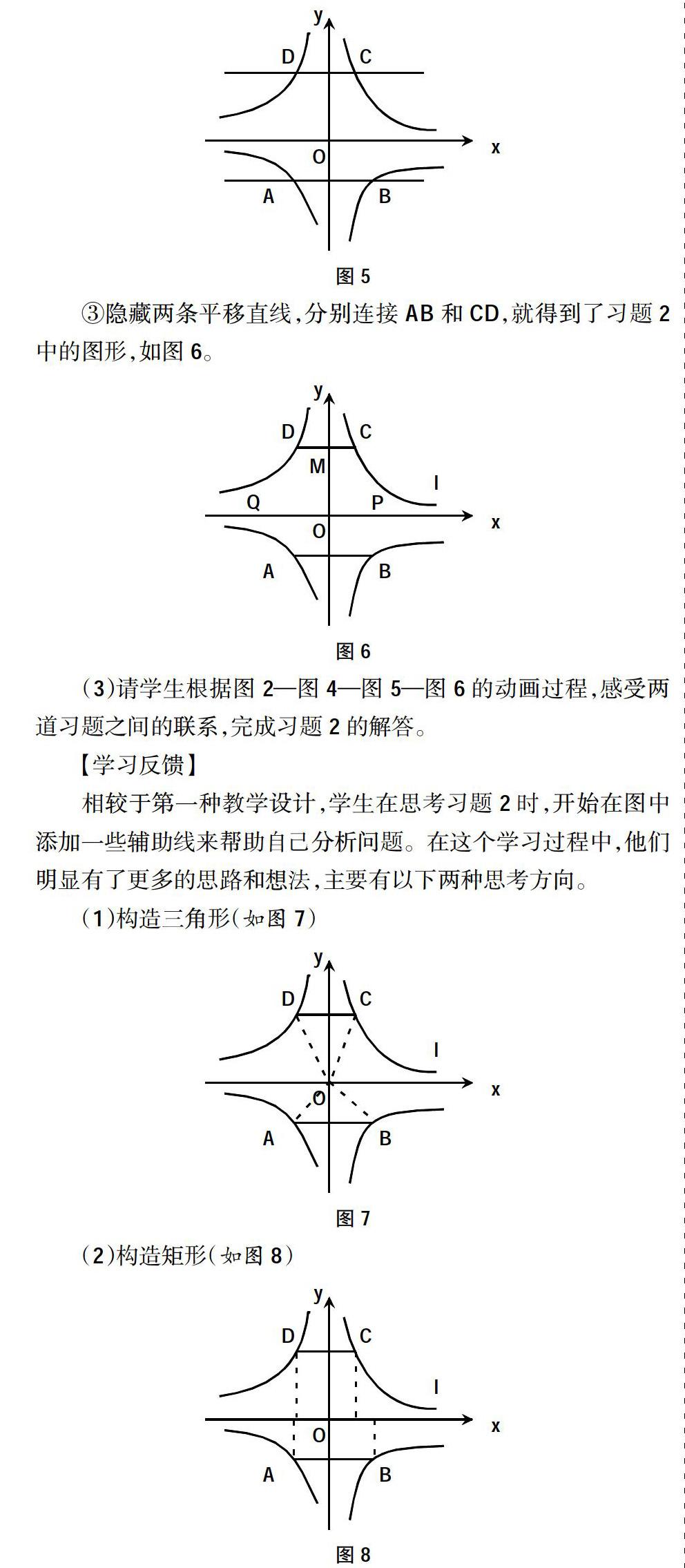
②让直线运动起来，向上平移与函数图象交于点D和点C，向下平移与函数图象交于点A和点B，如图5。

③隐藏两条平移直线，分别连接AB和CD，就得到了习题2中的图形，如图6。

（3）请学生根据图2—图4—图5—图6的动画过程，感受两道习题之间的联系，完成习题2的解答。

【学习反馈】

相较于第一种教学设计，学生在思考习题2时，开始在图中添加一些辅助线来帮助自己分析问题。在这个学习过程中，他们明显有了更多的思路和想法，主要有以下两种思考方向。

（1）构造三角形（如图7）

（2）构造矩形（如图8）

在巡视过程中，也有极个别学生在尝试用代数法解答，教师也及时给予了鼓励。通过学生的分享和讲解，这道中考压轴题得到了很好的解决。

【设计意图】

（1）从“一头雾水”到“逐渐明朗”

在案例中，虽然有模型一作为奠基，但是中等及以下的学生还是很难直接联系模型，作出相关辅助线来解决这道中考填空压轴题。这个时候，他们往往会表现出迷茫、焦虑，不知所措。因此，笔者在讲解习题2前，设置了与其相关，但相对基础的习题1作为铺垫。随后，通过动画，让学生发现习题2的图示就是由习题1演变而来，这一循序渐进的过程使得习题2的解法在学生的心中逐渐明朗。

（2）从“简单堆砌”到“连点成线”

上复习课最怕上成“习题堆砌课”！习题之间没有串联，生硬地呈现在学生的眼前。这样导致的结果就是哪怕经过教师非常辛苦的讲解，学生也只会“就题论题”，无法从整体的角度来完成一系列问题的解答。所以在案例中，笔者通过动画演示将两道习题巧妙地连接起来，让学生在不知不觉中感知两道习题之间存在的关联，自然地联想到解题的方向。

五、几点思考

（一）“只在此山中，云深不知处”需连点成线

许多时候，学生在解题过程中表现出来的“云里雾里”、不明所以，并不是真的因为他的能力不够或是他不努力，根本原因还是在于知识的“碎片化”。在这些学生的脑海中，一个个知识点就像是散落在地的小珠子。当他们需要这些珠子来帮助解题时，因为零散、无规律，就无法尽快从中找到有效的信息。那么，在一节复习课上，一根或多根串联知识点的细线就显得尤为必要。例如，在笔者的教学实践中，案例1的四个整式以及案例2的动画演示就分别充当了“连接线”的角色。

（二）“随题潜入心，润物细无声”让学法自然

心理学家皮亚杰认为：学习是主动建构的过程。因此，数学教学拒绝以割裂的方式将一个个习题强行“灌注”到学生的脑海里。在教学中，笔者建议让知识点或解题想法循序渐进地渗透到学生的内心深处，从而他们就能够在不知不觉中获得知识的洗礼，学习方法自然生成。例如，在案例1中，学生通过自己列式、辨析方程，构建了整式、方程、一元一次方程之间的联系，而笔者以问题串的形式，加以适当引导，在这样的一个互动过程中，相关概念就得到了很好的复习。案例2中，由习题1的图示通过动画演示逐步变形为习题2的图示，此时解题想法犹如涓涓细流，一点一滴地沁入学生的心扉，获得了复习的效果最大化。

（三）“欲穷千里目，更上一层楼”以整体视角俯视数学教学

作为奋斗在一线的数学教师，在教学过程中拘泥于眼前的章节或局限于某一个习题的解答是大忌！所以，无论是新授课还是复习课，笔者认为“大局观”非常重要。只有教师自己站在了知识链的顶端，才能以整体视角完成一堂课的教学。本文作为笔者对整体化教学的初步探索，着眼于复习课的课堂教学策略探究，仍然存在非常多的“未知”等待笔者去挖掘。路漫漫其修远兮，愿我们之后所做的一切教学研究都能够为触及金字塔顶端“添砖加瓦”！

参考文献：

[1]周晓琳.整体建构：初中数学复习防止“碎片化”[J].教师教育，2017（23）：94，126.

[2]周晓华.整体建构下的初中数学课堂教学策略[J].新课程（上），2011（2）：110.

编辑 王彦清