空间翻滚目标位姿耦合建模与运动特性分析

郝宇星，申 麟，李 扬

（中国运载火箭技术研究院研究发展中心，北京，100076）

0 引 言

空间失效航天器与太空碎片对正常运行的航天器而言是极大的威胁，发生碰撞会产生严重的后果。与传统的航天器的交会对接与编队飞行不同的是，这一类目标航天器不能提供自身的姿轨信息，其行为难以预测，可能会有翻滚等复杂运动状态，使得空间操作的安全性受到威胁。

翻滚是空间目标姿态运动的一种形式。在轨目标处于翻滚状态时，可以看做一个绕质心作定点运动的刚体。这种运动与翻滚目标的自身性质（如质量、惯量分布）以及初始状态有关。为了掌握目标器的运动状态，便于任务设计，需要对不同条件下的翻滚目标的运动规律进行研究。

在传统建模方法解决位姿耦合问题遇到瓶颈后，学者们尝试用新的数学工具进行姿态和轨道的统一建模。Brodsky等[1]基于 Pennock等[2]和 Adams[3]对旋量理论的研究，首先讨论了对偶惯性算子的本质和物理特性，然后使用对偶惯性算子和矢量变换规则得到对偶动量、对偶角动量、对偶力的一般表示形式，并基于这些定义推导以三维对偶形式表示的刚体动力学的牛顿-欧拉方程，为航天器一般性空间运动的研究和分析提供了理论基础。

在进一步的理论研究上，Wang等[4，5]推导了用单位对偶四元数表示的刚体转动和平动的动力学模型，指出单位对偶四元数是单位四元数的自然扩展，能同时表示旋转和平移，相对于齐次变换矩阵要用 16 个数来表示空间的一般运动，而对偶四元数仅仅需8 个数，另外，在计算效率上对偶四元数也高于齐次变换矩阵。在应用研究上，Wu等[6]使用对偶四元数来设计捷联惯性导航算法，并指出对偶四元数是同时表示刚体转动和平动最简洁和最有效的数学工具；Wang等[7]基于对偶四元数分别推导了交会对接最终段和两个航天器编队飞行的六自由度相对运动模型；Zhang等[8]推导了基于对偶四元数的刚体航天器平动和转动组合的跟踪误差模型。

使用对偶数和旋量可将刚体运动的平动部分与转动部分结合于一个框架之下，本文使用简明的模型，使用经典力学公式推导，得到由对偶数表示的牛顿-欧拉方程，该方程形式上与欧拉方程具有相似性，并且可以直观地看到姿轨耦合项的影响。

在对空间翻滚目标进行在轨任务前，需要对其运动状态进行分析。对于非合作目标而言，在无法获得其准确本体参数的条件下，需要根据其运动数据对其参数进行识别与估计，因此对翻滚目标的典型运动形式及其条件的分类格外重要。首先，本文将对翻滚目标进行分类，对不同类别目标的基本性质进行划分；在此基础上，应用位姿耦合动力学方程建立模型，分析在轨翻滚刚体的运动特点；最后给出 3种典型的姿态运动方式，并使用仿真举例说明其条件。

1 空间翻滚目标的分类及特征

根据任务对象的不同，可将空间翻滚目标分为：正常工作的航天器、功能受损（需要维修）的航天器、空间碎片或废弃部件与小行星等空间自然物体。由于针对这4类目标的任务各不相同，而且要考虑到各类目标的特性差异，翻滚带来的姿轨耦合程度也有所不同，在面对空间翻滚目标问题时，要对其特点进行分类，内容可以分为翻滚原因、翻滚速率、惯量阵特征、质量、耦合性以及主要任务目的。表 1为空间翻滚目标特征分类。

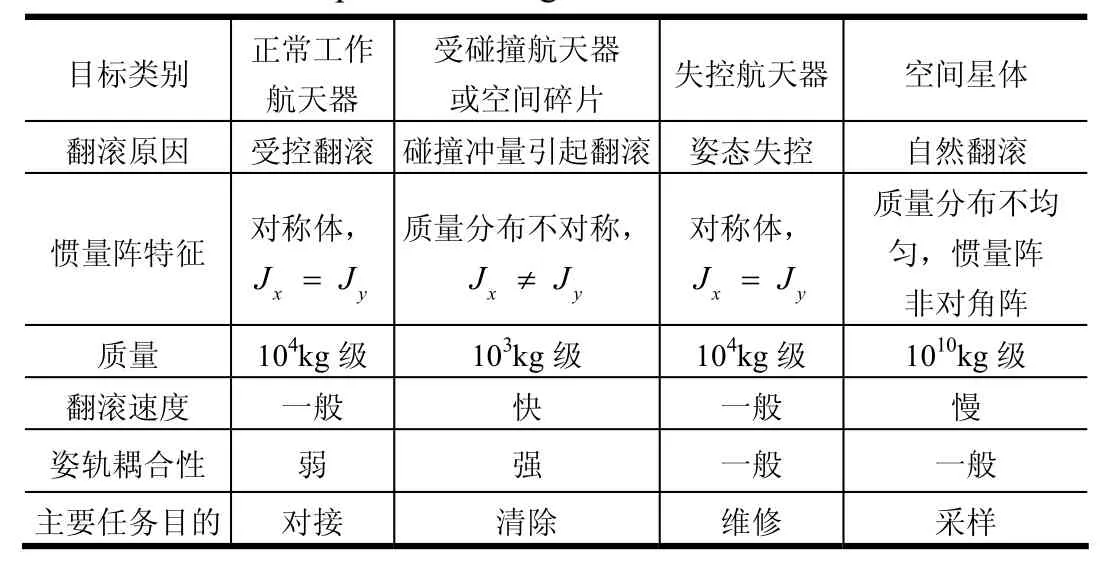
表1 空间翻滚目标特征分类Tab.1 Space Roll Target Feature Classification

2 空间目标位姿耦合动力学模型

本文采用对偶数与旋量的概念进行刚体的动力学方程推导，基于传统的理论力学原理，与新概念相结合，得到的结果表达形式简洁，物理意义明确，易于进行姿轨耦合分析以及一体化的任务设计。

刚体在三维空间的运动均可以表示为绕一轴线的旋转与沿该轴的平移，因此可将六维空间的向量称为一个旋量，映射一个三维刚体运动。几何上用六维列向量表示，代数上可用对偶数表示，形式如下：

式中 α，α′分别为主部和副部，或称为实部和对偶部，在表示物理量时，主部表示平移相关的量，副部表示旋转相关的量；ε为对偶单位，其性质为

设质量为m，质心为C的卫星在轨道上运行，并带有翻滚，如图1所示。建立卫星的本体坐标系bS，原点位于C点，X，Y，Z轴分别为卫星的3个惯量主轴。惯性系oS的原点为O。

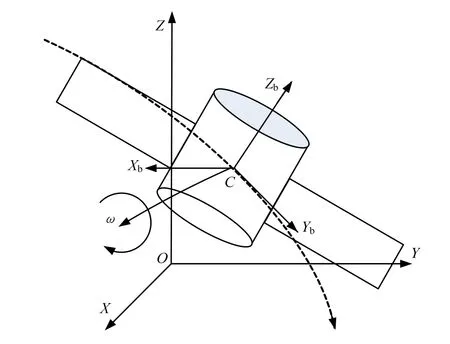
图1 航天器动力学模型示意Fig.1 Spacecraft Dynamics Model

将卫星视作刚体，则在时刻t，bS的运动状态由刚体的角速度矢量ω、C点t时刻的线速度矢量CV表示。

由于速度V与参考点有关，角速度ω与参考点无关， V与ω可构成以C为参考点的速度旋量，记为

由纯力F以及与该力作用线平行的力偶T组成的力，称为作用在旋量轴线上的力的旋量，简称力旋量。用对偶数表示，则为对偶力，记为

对于航天器而言，作用在其上的力分为控制力uF、地球引力 Fg、扰动力 Fd，力矩可分为控制力矩 Tu、重力梯度力矩 Tg和扰动力矩 Td。将这些力和力矩用对偶力概念统一起来，则作用在追踪器上的合外对偶力为

定义对偶惯性算子，由对偶质量算子与对偶惯量算子组成，记为

式（10）即为对偶力与对偶动量的关系式。根据矢量积运算规则改写为矩阵方程式，得到：

3 空间翻滚目标运动特性分析

将式（11）展开为实数部分与对偶部分：

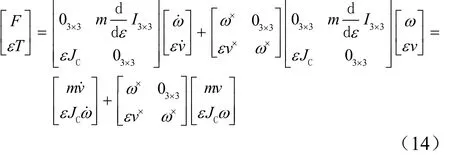
得到：

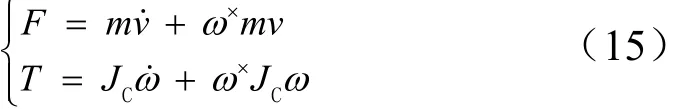
上述两组方程是相互耦合的，当以传统的方法研究航天器姿态运动时，通常把姿态运动对轨道运动的影响略去不计，且在分析姿态运动参数时，把轨道运动参数当作已知量，做这样的简化假设后，姿态运动方程便可单独进行积分计算。进行解耦后的姿态运动方程即欧拉方程，由式（15）可以看出它是对偶动力学方程的一部分，并在以下情况的翻滚目标其运动位姿耦合最为显著：

a）目标飞行器与追踪器的距离较近（几十米到几百米）时，此时平移量与旋转量处于相近的数量级，耦合项与非耦合项幅值接近；

b）目标飞行器的质量与惯量较大时，姿态运动导致的动量与角动量较大，对应的耦合量也较大；

c）目标飞行器存在复杂的姿态变化时，角速度项多变使得耦合项多变，影响其幅值以及方向。

对于无外力矩刚体的姿态运动问题，其解析解与几何解在理论力学中已有结论，其中的一般情形称为欧拉-潘索情形，其角速度轨迹在两个椭球的交线上。对于在轨自由运动的刚体而言，其受力主要为各天体的引力、引力梯度矩，其中以地球的引力与引力梯度矩为主，其余项可当作环境干扰力与力矩处理。由于引力梯度矩的值很小，并且工程上的航天器其质心与重心可近似重合，因此在短时间内可忽略；但在长期的轨道运行条件下，其对姿态积累的影响会十分显著。

针对在轨翻滚刚体的运动特点，以在轨翻滚航天器为例，通过设定不同的惯量矩阵、初始姿态、角速度的状态，根据刚体定点运动规律，进行举例分析：

假设某航天器轨道高度430 km，质量74 783 kg，处于圆轨道上做姿态运动，现使用对偶动力学模型，以航天器本体系作为计算坐标系，对各类转动情形进行数值仿真。

a）在轨定轴转动。

Jx= Jy= Jz时，过原点的任意轴都具有定向性；

Jx= Jy≠ Jz时，Z轴与Oxy平面的过原点的任意轴都具有定向性；

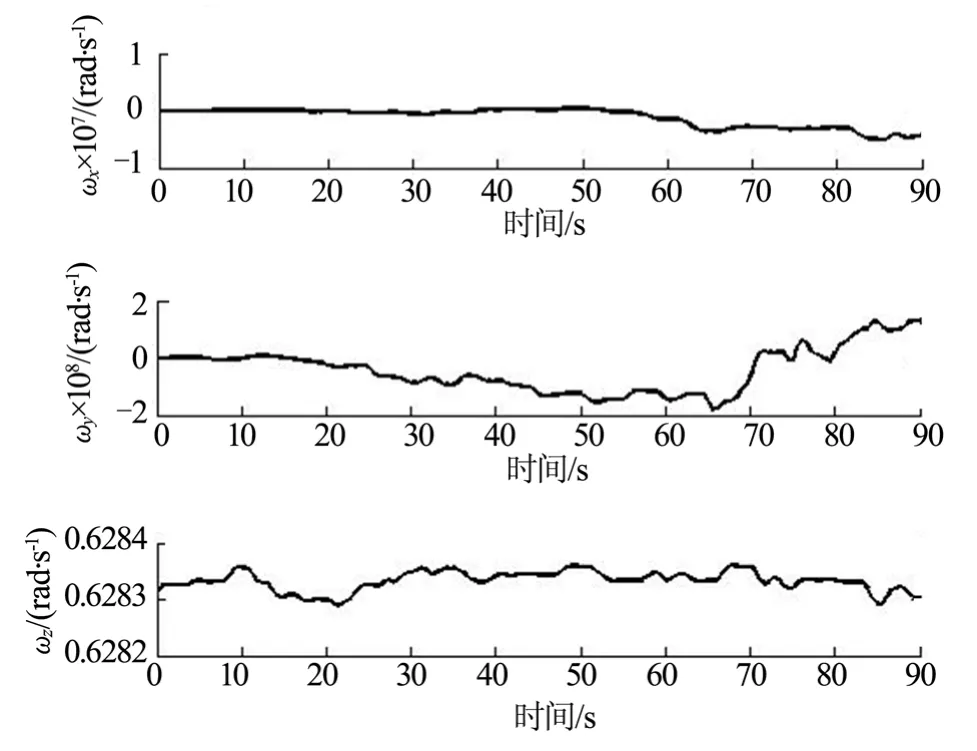
图2 在轨定轴转动时航天器角速度变化Fig.2 Spacecraft Palstance in Fixed-axis Rotation

图3 在轨定轴转动时重力梯度矩变化Fig.3 Gravity Gradient Torque in Fixed-axis Rotation

当满足定轴转动条件时，航天器转轴方向在惯性空间保持不变，且当转轴为Z轴时，旋转刚体受扰动后仍能保持在原来的方向近旁运动，或渐趋于原来的方向。正常工作的航天器往往处于定轴转动状态。由于惯量矩阵的3个分量相同，航天器受到的重力梯度力矩为零，因此航天器角速度基本不变，作定轴转动。

图4 在轨规则进动时航天器角速度变化Fig.4 Spacecraft Palstance in Regular Precession

图5 在轨规则进动时重力梯度矩变化Fig.5 Gravity Gradient Torque in Regular Precession

可以看出：当航天器角速度发生异常，但结构完好的情况下，航天器可能会规则进动。而这种角速度异常会由姿控系统故障引起。本例中航天器进动周期为 20 s，角速度矢量轨迹在本体系上为一个圆形，重力梯度矩在 ,XY轴上在零附近波动，而Z轴上进行周期变化。

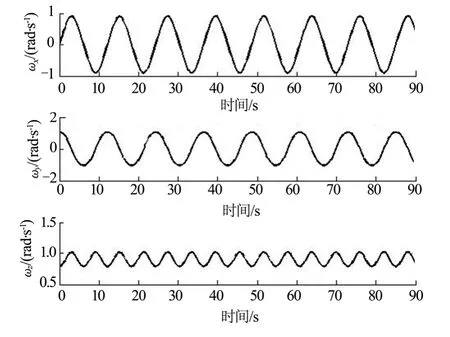
图6 欧拉-潘索运动时航天器角速度变化Fig.6 Spacecraft Palstance in Euler-poinsot Motion

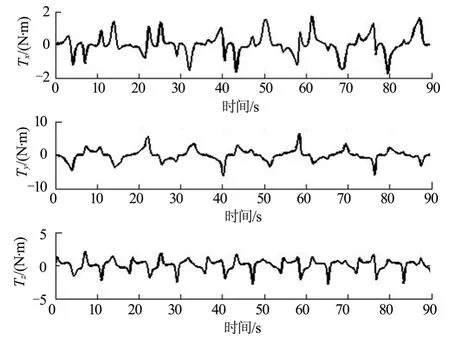
图7 欧拉-潘索运动时重力梯度矩变化Fig.7 Gravity Gradient Torque in Euler-poinsot Motion

图8 欧拉-潘索运动时角速度矢径变化Fig.8 Palstance Vector in Euler-poinsot Motion

对于不规则物体与随即状态而言，欧拉-潘索状态为最为普遍的运动状态。空间翻滚目标有大量的空间碎片以及小行星体，其质量与形状很不规则，姿态运动由碰撞产生，有很强的随机性，因此这类目标通常作欧拉-潘索运动。由结果可以看出，受到重力梯度矩的影响后航天器的Z方向角速度成周期变化，结合进动效果后角速度的轨迹在本体系中表现为马鞍面边际线（两椭球的交线）。

4 结 论

空间翻滚目标在轨道上虽然受到引力与环境干扰力的影响，但其姿态运动方式依然可以按照无外力矩刚体定点运动规律划分，并且根据其运动特征可以反推其质量特性，这对空间目标运动的识别与参数估计拥有重要参考意义。本文使用对偶数作为运动参数的表达形式，其输入输出均为6维，对于空间目标运动的初步识别与耦合估计非常实用，但为了得到更加精确的结果，仿真需要较高的运算精度，否则误差项的耦合放大会对结果产生很大影响，因此在解决高精度位姿估计问题时，需要对该仿真系统进行更深入的理论研究。