朴实中探究本质 简约中凸显思维
——2018年一道高考题的解法探究及深入思考
2019-02-18广东省广州市真光中学510380何淑龙
广东省广州市真光中学 (510380) 何淑龙
一、试题呈现
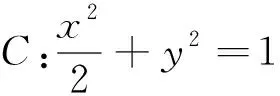
(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.
试题特征解读:该题是2018年高考新课标1理科卷第19题,主要涉及椭圆、直线的方程及其位置关系,试题设置两个递进的小问,第(1)问既减轻了考生的心理压力,又为第(2)问的探究设置了伏笔,构建动态的直线与静态的椭圆交汇,蕴涵着“定性”结论的成立,充分体现了数学新课标的理念,具有很好的区分度,是一道值得探究的好题.
二、解法探究
1.表征题目关键词
试题中给出了椭圆方程和直线方程,由于直线的不确定性,可知是经过焦点F(1,0)的直线系.“证明:∠OMA=∠OMB”等是关键词,审题时弄清含义、理解透彻所要思考的方向和具体操作所需要的方法与策略.“无论直线怎样变化,总有∠OMA=∠OMB”是几何问题(两个角相等),既可以用几何方法(直线AM的倾斜角与直线BM的倾斜角互补)也可以数形结合转化为代数方法(两条直线的斜率和为零)来解决,为寻找解题方法和思路做了一点提示,审题时需要注意.
2.解题思路分析
根据试题条件和上述分析可知,第(1)问先求出A,B的坐标,再由两点确定一条直线;第(2)问中∠OMA=∠OMB,将角转化为直线AM的倾斜角与直线BM的倾斜角互补,进而转化为直线AM的斜率与直线BM的斜率之和为0,再将其坐标化,即可列出相应的方程,可以从几个视角入手进行解题,来证明等式.


(2)解题方向:对于命题的证明,常常运用分析法及综合法相结合来进行思考,而直线的斜率k变动时,总有∠OMA=∠OMB,形成不同的解题思路和策略.
视角1 根据上述分析将直线AM,BM的斜率之和表示出来,利用“kAM+kBM=0”来证明“当直线AB的斜率k变动时,总有”∠OMA=∠OMB”成立.

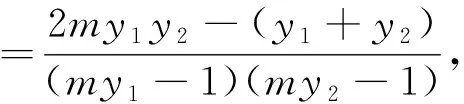
则直线AM的倾斜角与直线BM的倾斜角互补,故∠OMA=∠OMB.

证法2:根据上述分析将直线AM,BM的斜率之和表示出来,利用“kAM+kBM=0”来证明“当直线AB的斜率k变动时,总有“∠OMA=∠OMB”成立.



视角3 根据题目第(2)问的条件“当k变动时,总有“∠OMA=∠OMB”可知,角∠AMB的对称轴就是x轴,由轴对称的性质可知,直线AM与直线BM关于x轴对称,具体化有点A关于x轴的对称点A′一定在直线BM上,故有下面证法.
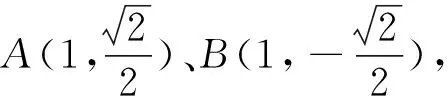

视角4 根据题目第(2)问的条件“当k变动时,总有“∠OMA=∠OMB”可知,结合图形特征,MO是∠AMB的角平分线,只需证点O到直线MA和MB的距离相等,沿着这个思路有下面方法.


当直线l与x轴垂直时,得到x1=x2,所以①式成立,故∠OMA=∠OMB.
当直线l与x轴不垂直时,x1≠x2,∴3(x1+x2)-4-2x1x2=0,以下同解法2.

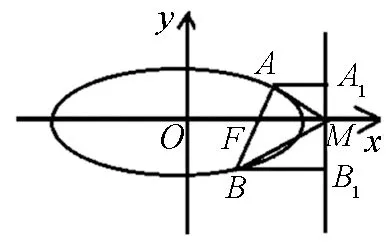
图1
证法5:过点A,B分别作椭圆右准线的垂线,垂足分别为A1,B1(如图1所示)
三、试题溯源
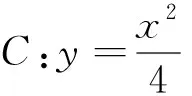
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
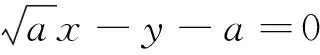
(Ⅱ)当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以P(0,-a)符合题意.
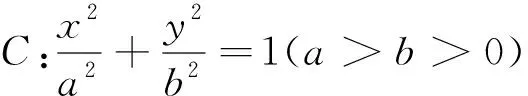
(Ⅰ)求椭圆C的方程,并求点M的坐标(用m,n表示);
(Ⅱ)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.
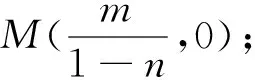
该试题的第1问是由题源1的第一问巧妙特殊化,求直线方程(该直线方程实际上是椭圆的切线),问题的设计降低难度,学生对问题易切入,让学生信心倍增.试题的第2问是题源1的第2问的探究性问题整合而成的命题证明形式,把题源1使得当k变动时,总有∠OPM=∠OPN中的“当k变动”省去,增加问题的难度,对直线的斜率是否存在进行分类讨论,加大了思维强度和广度.
该试题第2问命题的证明是题源2探究问题的形式似曾相识,但是该题的问题指向性更具体明了,题源2中对称性、字母的抽象性、探究是否存在等设计省去,有效地降低试题难度,但是该试题设计为命题的证明,有效地检测学生对问题的开展探究、观察、联想、推理等能力的考查,对学生的逻辑推理、数学抽象、直观想象、数学运算和数据分析等核心素养的考查,有意导向、强调教学过程增强数学学习的探究活动,对学生核心素养的培养,凸显了命题专家的良苦用心和对中学教师教学的一种期望.
四、试题拓展
该试题第(2)问的一般化形式(以焦点在x轴为例):
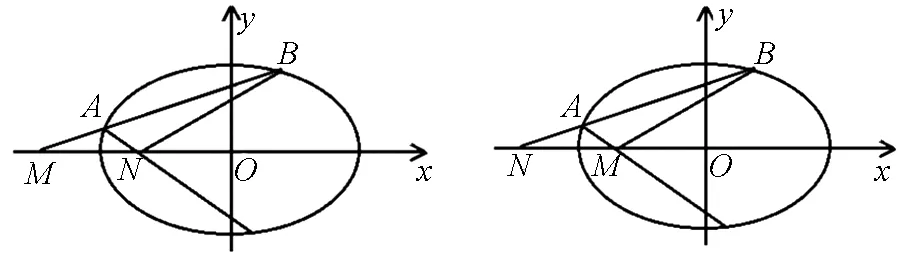
图2图3


将上述的结论1类比到双曲线、抛物线可得:

结论3 已知M(m,0),N(-m,0)(m≠0)是抛物线y2=2px(x>0)的对称轴上两个点,过点M作与坐标轴不平行的直线l与抛物线相交于A,B两点,则直线AN和BN与x轴成等角.
将上述结论1、结论2、结论3,可以统一为圆锥曲线的一个性质如下:
已知M,N是圆锥曲线的对称轴上两个点,过点M作与坐标轴不平行的直线l与圆锥曲线相交于A,B两点,则直线AN和BN与x轴成等角.
