基于新型变换域的低截获技术

李 勇，宋志群，沙学军

(1.通信网信息传输与分发技术重点实验室，河北 石家庄 050081；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；3.哈尔滨工业大学通信技术研究所，黑龙江 哈尔滨050001)

0 引言

在无线通信传输过程中，传统的通信安全性保障以基于密码学为主，通过将信息进行密码学算法的处理来隐藏保护信息。密码学技术的安全性主要取决于当前计算机的计算能力，也就是以计算复杂度来实现计算安全性，但这种方法终将会随着未来计算机的计算能力不断提高而失效[1-4]。

现在通信主流的安全性保障技术集中在物理层安全上，主要分为3个方面：一是将信号隐藏在噪声里，通过接收端的处理得到有用信号，典型的技术是扩频技术；二是利用传输信道的短时突发特性，使得信号被截获的概率降低，典型的技术是利用多天线技术；最后还有学者研究将传输波形进行预处理，使得在信道上传输的波形发生明显变化，从而达到信号伪装、躲避非合作方检测的目的，典型的是变换域的低截获传输技术。它是一种新型的抗截获方法，融合了传统单载波和多载波系统在复杂环境中的优势，并且在时频双选信道下，能够表现出明显的系统优势[2-4]。本文从抗截获技术发展的角度，介绍多种复杂环境下的抗截获技术，重点介绍基于加权分数域的抗截获技术的优势，并且与传统的单/多载波进行性能对比与分析，对复杂环境下的性能进行分析总结，为实际通信工程应用奠定理论基础。

1 抗截获技术的发展现状

国内外相关研究学者已经提出了多种低截获概率方法，从作用不同的域来看，一般可以分为时频域抗截获技术、能量域抗截获技术、空间域抗截获技术以及变换域抗截获技术等，如图1所示。

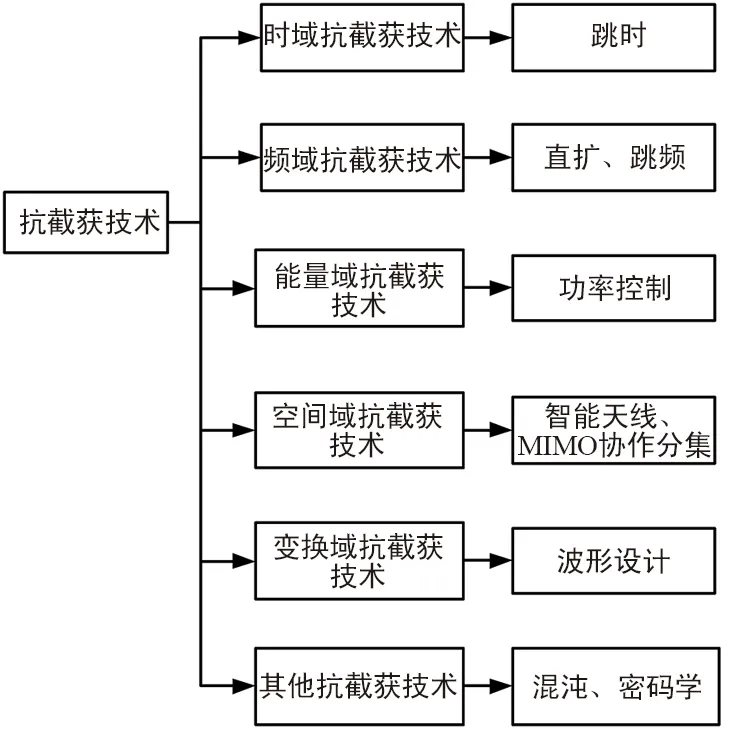
图1 抗截获技术主要方法总结

传统的时域抗截获手段有跳时(Time Hopping,TH)，而频域的抗截获技术包括直接序列扩频(Directed Sequence Spread Spectrum,DSSS)及跳频(Frequency Hopping,FH)[5-7]等。

能量域抗截获技术主要是对发射信号的功率进行很好的管理和控制，以躲避非目的接收机的截获。截获距离的计算公式为：

(1)

式中，Ri为截获距离,Pt为通信辐射功率,Gti和Git分别为通信天线在侦收机方向上和来波方向上的增益,λ为波长,Li为侦收机噪声功率谱密度,Si/Nsi为侦收机截获信号所需信号功率与噪声功率谱密度的比值。

从式(1)可以看出，Ri越小，抗截获性能越好。未来减少截获距离，可以采用对发射功率进行控制和减少侦收机方向上的增益。这种技术是目前最好的抗截获技术，但是需要功率精确控制，主要有开环功率控制和闭环功率控制。但是缺点也比较明显，功率控制的精度直接影响了抗截获性能，为了控制功率精度，额外开销也是比较大的。

空间域抗截获技术主要应用方向是智能天线，对信息的保密主要利用噪声、信道衰落等信道的特性。这种方法是通过利用物理层特征使非合作方无法准确接收信号，从而很难获得有效信息，而不是利用密码学的算法来进行信息保护。因此物理层信息安全不会因为计算机能力的提高而失效。

多天线技术[8]在物理层安全的研究中得到了广泛应用，它采用多发单收的天线系统模型，这种模型既能提升系统保密容量，还能与波束成形、人工噪声等技术完美结合，有效提升保密性能。另外一种方式是利用协作中继来保证安全通信，主要目的是提高保密容量。

这2种方案存在的主要问题是，当非合作方和合法接收方物理距离比较接近时，且非合作方已知合法接收方的训练序列及他们之间的信道信息，非合作方可以通过还原周围无线信道环境，并且仿真出信道信息，从而实现信息截获的目的，这是已有学者根据信道互异性的物理层信道特征提取算法得到的结论。因此，如何应对物理距离接近合作方的窃听问题，是物理层安全技术要解决的重要问题。

变换域通信系统[9]是一种具有低截获传输波形，并且具备信道感知的无线电通信技术，在复杂环境适应性上优势明显。其基本思想是通过信道感知，在已知系统带宽内，寻找未被干扰或者占用的频段进行通信，躲避已经干扰或被占用的频段，并且利用变换域算法合成类高斯噪声的调制信息，达到低截获抗干扰的目的。

混沌技术作为一种低截获技术，主要是利用混沌现象的特点：非周期、不收敛及有界性，尤其对初值条件极为敏感。混沌信号具有类高斯的特性，这使得这种信号天生具有低检测的特性。混沌技术的主要问题在于收发端的同步问题，由于其对于初值的敏感性，如果不能精确同步，将对解调产生巨大的影响，从而增加了接收端的复杂度。

总之，目前的低截获技术仍然以直扩等传统技术为主，新理论、新技术发展缓慢，这样带来了抗截获手段单一，截获技术针对性更强，对于系统安全性提升不利，迫切需要在新技术上有所突破，这也是信息对抗未来发展的趋势，为此提出基于新型变换域的低截获技术，希望在物理层安全上发挥作用。

2 基于变换域的低截获技术

1995年，C.C.Shih提出了区别于经典分数傅里叶变换的加权分数傅里叶变换[10-11](Weighted type Fractional Fourier Transform,WFRFT)，它由一系列函数进行加权求和而得到，相比于经典分数傅里叶变换，由于实现方式和离散算法更加简便[12-15]，因此，可应用在高数据速率传输系统中。

2000年，Cariolaro等人总结了经典和加权类分数傅里叶变换这2种变换的定义形式，把满足以下线性、退化性及调制阶数可加性3个条件的算子Fα(α∈R)，称之为分数傅里叶变换算子：

Fα+β=FαFβ=FβFα,α,β∈R。

(2)

并且把平方可积函数f(t)的分数傅里叶变换定义为下述一般形式：

(3)

这里，ψα(u,t)是分数傅里叶变换的核函数，可以定义为以下2种形式：

(4)

(5)

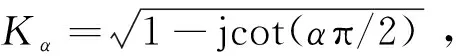
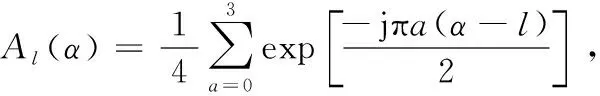
(6)

从式(6)可以看出，当变换阶数为α=0时，只有A1的模不为零，而A1对应的加权项恰好是原信号，也就是单载波信号；另外当α=1时，只有A2的模不为零，而A2对应的加权项恰好是原信号的傅里叶变换，也就是多载波信号；当0<α<1时，这时的信号是单载波和多载波信号的融合。

纵观整个加权分数傅里叶变换的发展，主要分为2个阶段。一是理论发展阶段，这个阶段开始于C.C.Shih在1995年提出的四项加权分数傅里叶变换概念，主要受基于CFRFT的光学研究的启发。基于CFRFT的光学研究认为，光在折射率渐变介质中传播，当达到傅里叶变换结果时的传播距离为L，则认为光在到达L之前的某个位置αL，就是完成了阶数为α的经典分数傅里叶变换，C.C.Shih认为变换阶数与光传播距离的表示关系不唯一，从而提出一种新的分数傅里叶变换，即加权分数傅里叶变换[11]。Liu在1997年总结4-WFRFT理论的基础上，认为任意4r(r∈Z)的变换也是成立的，因此提出4r-WFRFT，其实是将4-WFRFT进行了推广。之后，Carilaro在2000年提出分数傅里叶变换的一般定义，统一了经典和加权类的分数傅里叶变换，并且提出多参数的4-WFRFT变换的概念，对于4-WFRFT进一步推广，Ran在2005年将加权项数进一步推广到任意大于3项的整数，由于加权系数的不同，因此属于不同的加权分数傅里叶变换。Lang在2008年进一步将项数和参数均推广到任意整数，得到多项多参数分数傅里叶变换(MPFRFT)，这一时期加权分数傅里叶变换的研究主要集中在理论研究，研究者大多是数学领域或者光学领域，工程上研究主要是在图像加密方向，并未涉及到无线通信理论。

加权分数傅里叶变换的通信应用发展历程开始于2010年Mei在其博士论文里揭示了4-WFRFT的物理意义： 4-WFRFT变换实际上是2路单载波信号和2路多载波信号的加权求和。在此基础上，Mei展望了其在抗干扰抗截获方面的优势。2012年，Qiu发表一篇关于基于4-WFRFT的码分复用(CDMA)系统的论文，将4-WFRFT应用到CDMA系统中。2013—2014年，Wang和Li根据4-WFRFT在双选信道下的抗衰落特性，提出基于4-WFRFT的混合载波系统的信道均衡技术研究，相比较于传统单载波和OFDM系统，在双选信道下误码率性能得到进一步的提升。同时在2014年还有学者研究了基于4-WFRFT的峰均比抑制问题，由于4-WFRFT是单载波和多载波系统的融合，因此也融合了单载波在峰均比方面的优势，相比较于OFDM系统，峰均比大大降低。2015年，Mei研究了基于4-WFRFT的窄带干扰抑制技术，提出对抗恶意干扰的混合载波系统的信号设计原理。2016年，Fang将混合载波系统和直扩技术相结合，进一步提升了混合载波系统的抗信息截获性能，同时空军工程大学的X.Da提出基于4-WFRFT和人工噪声的变换域通信技术。2017年，有学者将混合载波系统和波束成形技术相结合，提出基于混合载波-部分FFT波束成形技术，提升了系统传输效率。

综合以上加权分数傅里叶变换通信中的应用，主要是集中在4-WFRFT变换的应用上，至于多项加权以及多项多参数加权分数傅里叶变换尚未在通信中得到很好的应用。

3 基于加权变换域的抗截获性能分析

首先给出基于WFRFT的变换域通信系统模型，其原理框图如图2所示。

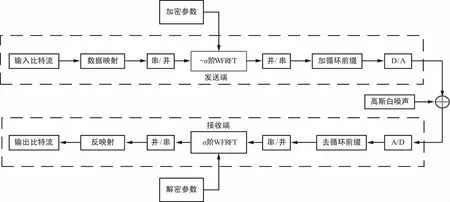
图2 基于WFRFT的变换域抗截获通信系统

对于WFRFT抗截获通信系统，发端需要在加密参数以及调制阶数-α的控制下，对调制信号进行处理，接收端需要在同样的解密参数以及α进行信号正常解密，如果接收端无法得到正确的加密参数，则无法对信号进行正确解调。

星座图分析可以在一定程度上对发送信号的调制方式进行破译，将利用星座图来分析双参数加权分数傅里叶变换的可靠性。而对于非合作方有2种情况：一是未知双参数加权分数傅里叶变换，二是已知存在这种变换，但是参数配置以及调制阶数未知。下面分别针对这2种情况进行星座图识别的仿真分析。

从图3中可以看出，对于非合作方未知双参数加权分数傅里叶变换，认为信号就是高斯噪声，对于非合作方不会看成是信号，达到隐藏的目的，但是相应的合作方可以很好地解调信号。

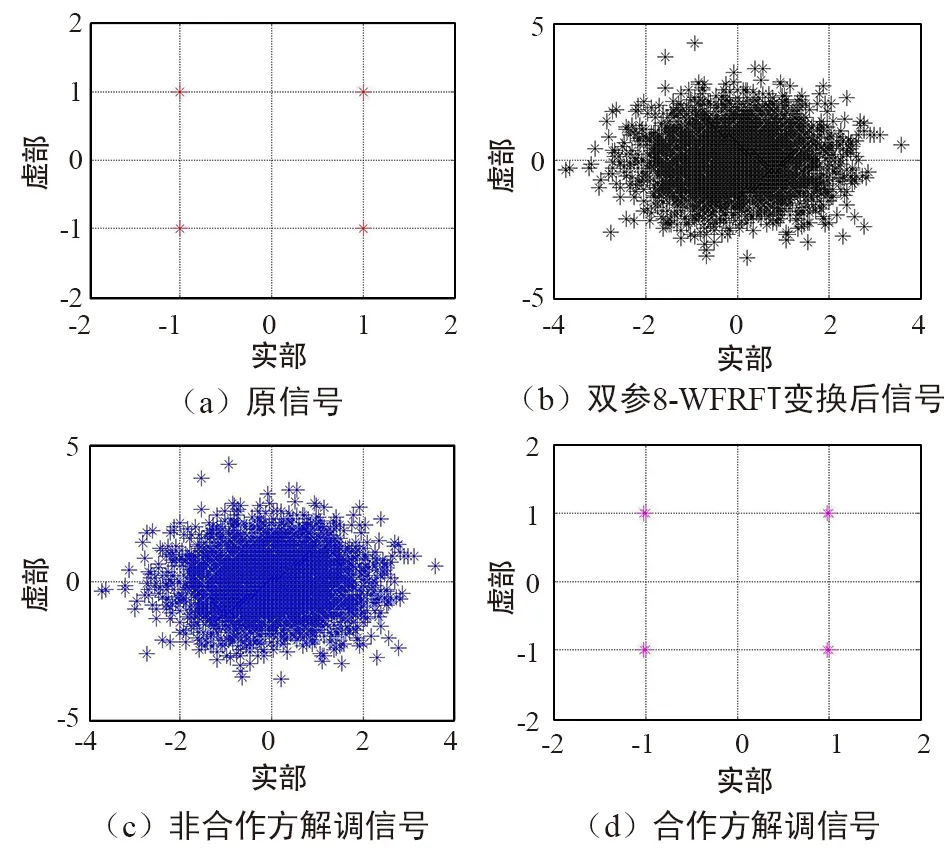
图3 8-WFRFT变换后的信号隐藏效果

对于非合作方已知双参数加权分数傅里叶变换情况下，可能会进行双参数加权分数傅里叶逆变换破译，但是如果不知道准确的参数，仿真结果如图4所示。

图4 8-WFRFT变换后的信号隐藏效果

图5 8-WFRFT变换后的信号欺骗效果

随着不同的调制阶数扫描误差误码率的变化如图6所示。从图6可以看出，随着误差的增加，扫描误码率将会上升，当扫描误差达到2%时，误码率开始上升，并且开始影响正常解调。当扫描误差超过4%时，误码率上升一个数量级，几乎无法进行解调，说明双参数分数傅里叶变换对于调制阶数的敏感性。

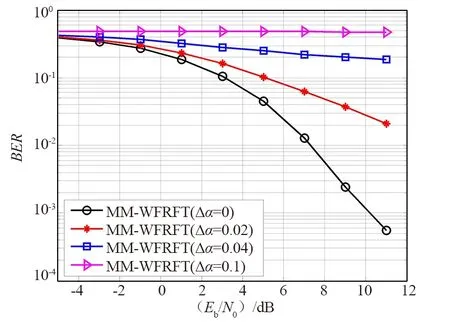
图6 随着不同的调制阶数扫描误差误码率的变化

4 结束语

对抗截获技术进行总结分析，并且对基于加权变换域的抗截获技术进行了重点研究。利用基于多参数加权分数傅里叶变换的抗截获技术，通过数值仿真，对合作方和非合作方接收信号进行了对比实验，验证了基于加权变换域的抗截获技术可以在星座图识别上达到隐藏信号的能力，增加了非目的接收方对信号的正确识别和检测的难度。通过参数扫描的方法，对基于双多参数加权分数傅里叶变换的抗截获技术的参数敏感性进行了分析，结果表明提出的算法在参数扫描误差>4%时，非合作方无法正确解调信号，也证实了该算法抗截获性能的优势。