全海深载人潜水器超高强度钢制载人球壳的极限强度分析与模型试验

于 爽 ，胡 勇 ， 王 芳 ，杨青松 ， 崔维成

（1.上海海洋大学 工程学院，上海 201306；2.上海深渊科学工程技术研究中心 上海海洋大学，上海 201306）

0 引 言

近几年，国际上已在全海深载人潜水器技术上展开激烈的竞争，若我国能在作业型载人潜水器研制中抢得先机，不仅有利于巩固我国在海洋技术上的领先地位，还有助于推动我国在深海科学技术上的发展。

全海深作业型载人潜水器作为当今世界上最为先进的海洋装备的一部分，能够搭载科学家深入大洋深处，直观地进行科学考察与研究工作，在研究海洋地质、资源调查、研究深海生物、海洋化学等方面拥有着不可替代的作用[1]。载人舱耐压球壳是全海深载人潜水器的关键部件之一，在承受交互变化的静水压力以及深海未知环境的情况下，需保证舱内人员安全以及设备的正常运行。因此，耐压球壳需要有足够的强度，但同时应尽量减小重量，以免影响潜水器的总体性能和重量指标[2]，各大船级社潜水器和潜水系统规范中对潜水器耐压壳体的设计和制造方法都进行了描述[3-8]。

开展基于超高强度马氏体镍钢的耐压结构材料性能研究及球型结构静水压力作用下的结构强度计算方法研究，是研制11 000 m全海深载人潜水器“彩虹鱼”号载人舱的首要问题，也是核心关键问题。上海海洋大学深渊科学与技术研究中心在上海海洋大学和上海彩虹鱼海洋科技股份有限公司联合资助下，开展11 000 m级全海深载人潜水器“彩虹鱼”号的研制工作，采用曾在两台6 000 m级“和平”号载人舱上所使用过的马氏体镍钢（18Ni250）来制造全海深载人舱。因此，基于现有的规范设计方法[3]和大深度载人深潜器的前期研究成果，本文通过模型球压力试验验证马氏体镍钢耐压球壳的设计和分析方法，为研制11 000 m载人舱提供理论和试验基础。

1 模型设计与验证

1.1 压力设备和模型球参数

根据目前全海深海洋环境模拟设备限制条件，即目前深海压力环境模拟设备最大内径为1000 mm，最高承压140 MPa，以及全海深载人潜水器研制需求，所提出的模型球的内径为800 mm，设计估算的极限强度载荷控制在110 MPa左右。模型球的设计参数见表1，马氏体时效镍钢材料机械性能见表2。

表1 设计输入参数Tab.1 Design parameters

表2 球壳物理参数Tab.2 Physical parameters of the spherical shell

1.2 模型球设计标准

根据《潜水系统和潜水器入级规范》[3]，假定耐压壳体厚度为t，球壳薄膜应力计算如下：

其中：R0为球壳外半径，Rm为球壳中面半径，Ri为球壳内半径，P为最大工作压力。

而球形耐压壳体的极限强度计算方法则规定如下：

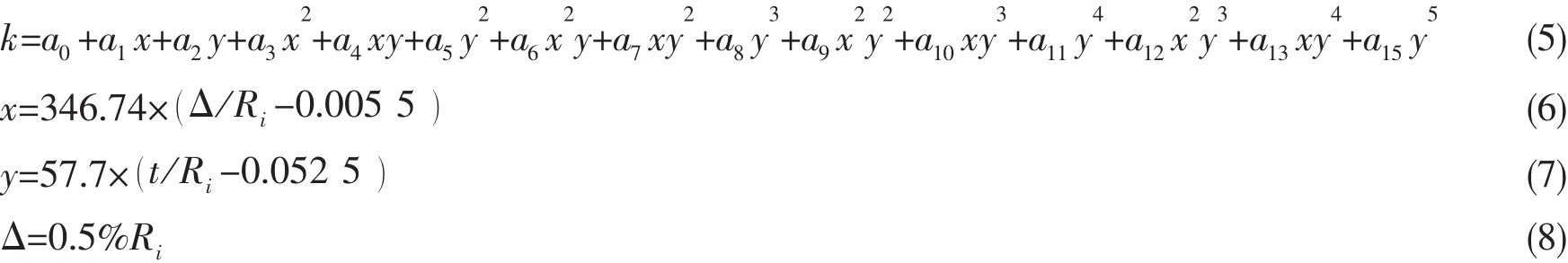
其中：k为制造偏差修正系数，Δ为球壳最大制造允许误差，Pcr为耐压球壳破坏压力。

公式（5）中各项系数取值如表3所示。

表3 公式（5）中系数取值Tab.3 Coefficients in formula(5)

有限元分析设计耐压壳体时其强度规定执行如下控制标准，即在最大工作压力P作用下其应力强度满足如下规定：

（a）薄膜应力强度：

（b）平均薄膜应力+弯曲应力强度：

（c）峰值应力强度：

（d）对于极限承载压力则要求其满足如下规定：

即耐压球壳结构安全系数保证不小于1.5。

2 数值分析

2.1 耐压球壳厚度计算

模型球内径为Ri=400 mm，破坏压力目标确定在Pcr=110 MPa，则相应此破坏压力的最大工作压力为P=Pcr/1.5=73.3 MPa。 由公式（3）、（4）、（5）、（6）、（7）和（8）可得到满足屈曲条件的最小厚度为：t=13.5 mm，综合考虑球壳在整个载人潜水器中的整体比重，取t=13.5 mm。其简化模型如图1所示。

图1 耐压球壳简化模型Fig.1 Simplified model of the spherical shell

2.2 许用应力计算

参照《潜水系统和潜水器入级规范》16.1.5.1[3]，计算耐压壳体承受最大工作压力时，要对包括开孔在内的球壳结构进行有限元应力分析，且符合下述衡准：

（1）耐压壳体的平均膜应力应不超过材料屈服强度的2/3，即：

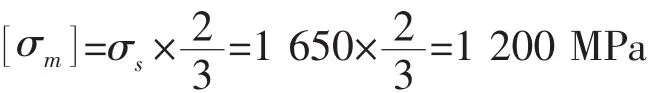
（2）不计局部应力集中的平均膜应力和弯曲应力的组合应力，应不超过材料屈服强度的3/4，即：

（3）计及局部应力集中的耐压壳体任一点处的最大峰值应力应不超过材料的屈服强度；但如果最大峰值应力是压应力，则最大峰值应力可允许超过材料拉伸屈服强度，但应不超过材料拉伸极限强度。即：

2.3 有限元计算

传统的薄壳理论认为静水压力不断增加的情况下，薄壳将发生线性屈曲，其临界应力等于失稳后的应力。而由公式（4）得出全海深球模型属于厚壳，屈曲前材料就已经处在非线性阶段，失稳后材料丧失承载能力。并且初始缺陷对球壳的临界载荷也有一定的影响。

（1）边界处理与网格划分

耐压球壳受到静水压力时不受任何约束，考虑耐压球壳是对称结构，因此取四分之一上半球，在边界上施加对称条件，球壳外表面施加静水压力。考虑该耐压球壳属于厚壳，厚度半径比较大，采用六面体自由网格划分，然后对上半球四分之一球壳分三部分，划分后的网格如图2所示。

（2）静力学分析

简化螺栓孔等特征后，建立1/4上半球模型，对称面受到无摩擦法向接触约束。设计耐压球模型的工作载荷为73.3 MPa，根据规范[10]要求极限承载压力至少应为最大工作压力的1.5倍，因此在海水接触面施加110 MPa压力。其分析结果如图3所示，从图中可以看出，几何形状突变区域应力为1 393.8 MPa。表4为上半球的应力计算结果。

将厚度t=13.5 mm代入（1）式中得到：

图2 1/4上半球网格划分Fig.2 Grid partition of a quarter hemisphere

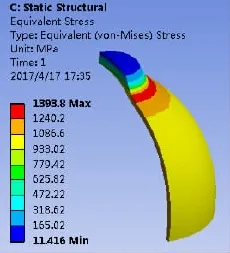
图3 73.3 MPa压力下的上半球应力分布云图Fig.3 Stress distribution of the upper shell under the pressure of 73.3 MPa

表4 上半球应力计算结果（计算压力110 MPa）Tab.4 Stress calculation results of the upper shell under the pressure of 110 MPa

（3） 屈曲分析

设定材料双线性各向同性硬化参数，屈服强度1 650 MPa，切向模量0 MPa，根据球壳圆度的测量结果，取线性屈曲一阶模态的3%作为几何缺陷。对上半球进行材料及几何非线性屈曲分析，时间120 s分为120步，每增加一步代表载荷增加1 MPa，结果如图4所示，结构在压力106.8 MPa时达到极限载荷。图5是在屈曲分析时，结构放大78倍后的合位移效果图，最大位移为2.675 mm，发生在应力集中区域，也就是几何形状突变位置。

图4 上半球极限载荷分析Fig.4 Limit load analysis of the upper shell

图5 上半球失稳波形Fig.5 Instability waveform of the upper shell

3 模型试验

为了验证该设计方法在马氏体镍钢耐压壳设计的适用性，本文首先设计了缩尺比模型，通过缩尺比模型的极限强度考核验证载人舱的设计标准。模型试验中，将贴着应变片的耐压球壳放入极限压力为140 MPa的压力筒内，图6为耐压球壳模型，内直径800 mm，厚度为13.5 mm，球壳由上下两个半球通过螺栓连接在一起。上半球开有三个孔，用来安装穿舱件，连接球壳内外应变片。开口的下面设计有应力加强部分，其中开孔的最高点距离圆心的半径为432 mm。

图6 试验样球Fig.6 Test model

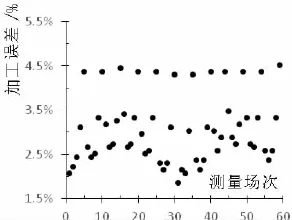
图7 球壳加工误差（%）Fig.7 The manufacture tolerance of the spherical shell

3.1 测试准备

测试前，为了减少理论分析与试验验证在客观上存在的显著差异，需要对球壳的厚度进行测量，结果如图7所示。从图中可以看出，第一行的数据误差最大，显然是耐压球球壳上几何形状突变区域；另外球壳在加工后确实存在一定的初始缺陷。

在球壳的不同位置上贴应变片，其贴片方案如图8、9所示。贴应变片时需对球壳表面进行处理，保证应变片和球壳表面的最大接触，用外部导线连接到一台静态应变仪上，再给球壳内部充满水，防止球壳在破坏分析阶段的突然失效损伤压力筒。

3.2 测试过程

设备调试完毕之后，将待测球壳放入筒内，记录球壳在交变载荷作用下的应力应变值和球壳的收缩率。本文主要针对前者。压力筒的施压过程如图10所示，第一个循环阶段每三分钟加5 MPa，加至70 MPa用来测试球壳在屈曲变形阶段前的应力应变值，第二个阶段前期每三分钟加5 MPa，等接近理论极限载荷时，每分钟加3 MPa、1 MPa或0.5 MPa等，如图10所示，尽可能准确地得到球壳在后期非线性变形下的失效载荷。

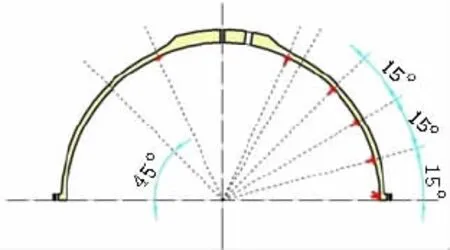
图8 上半球内表面贴片方案Fig.8 Positions of the strain gauges inner the upper shell

图9 上半球外表面贴片方案Fig.9 Positions of the strain gauges outer the upper shell

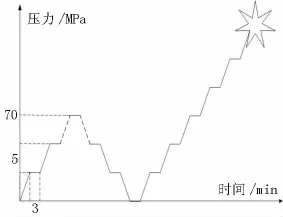
图10 试验施压过程Fig.10 Loading process during the test

图11 117 MPa压力下破坏后的球壳Fig.11 The damaged spherical shell when pressure reaches 117 MPa

3.3 测量结果

根据上述试验，测得了耐压球壳在不同大小的静水压力下的应力应变值，以及球壳破坏时的最大载荷，并发现发生失效的位置在几何形状变化点。其中球壳上几何形状规则区域和突变区域的应力应变曲线如图12所示。从图中可以看出，几何形状变化区域的临界载荷为104 MPa，而几何形状规则区域的临界载荷为107.1 MPa，与ANSYS理论分析结果基本一致，说明了该马氏体镍钢的材料性能和制造工艺达到了理论预报的要求，可以用于整球的制造。

图12 结构几何变化区域和规则区域应变对比Fig.12 Stress versus strain in geometric change location and regular location

4 结 语

本文主要针对内半径为400 mm、厚度为13.5 mm的马氏体镍钢耐压球模型进行了极限强度分析和压力试验测试，得到了球壳的破坏强度和失效载荷，并得出如下结论：

（1）从有限元分析结果和试验验证得出，试验分析和有限元分析的结果相吻合，非线性有限元分析方法分析载人潜水器耐压球壳的稳定性具有一定的可靠性。

（2）有限元分析时，球壳的厚度、圆度、初始缺陷等对球壳极限承载能力均有显著影响，球壳屈曲变形发生在几何形状发生变化的部位。

（3）模型试验证明了设计规范用于马氏体镍钢耐压壳设计以及18Ni250材料作为全海深载人潜水器耐压球壳材料的可行性。

该文中的试验验证和理论分析，均是对简化后的未开孔球壳的，实际的潜水器耐压球壳整球开有人员出入口和观察窗等，因此还需要进一步开展马氏体镍钢开孔球壳极限强度的研究。