基于相对熵的区间Pythagorean模糊多属性AQM决策方法及其应用

李 娜， 高雷阜， 王 磊

(1.辽宁工程技术大学 基础教学部，辽宁 葫芦岛 125105；2. 辽宁工程技术大学 理学院，辽宁 阜新 123000)

0 引言

多属性决策(MADM)是指具有多个属性的有限方案排序和选择问题，其理论与方法在经济、管理、工程和军事等诸多领域具有广泛的应用[1]。赵萌等[2]利用相对熵替代经典TOPSIS方法中距离，将其应用到MADM领域，Navarrete等[3]提出了一种AQM(Alternative queuing method)决策方法。由于受客观环境的复杂性、决策者的专业水平以及知识结构等因素的影响，决策者难以给出精确的属性值信息，往往用模糊数(FS)[4]，直觉模糊数(IFS)[5]或者区间直觉模糊数(IVIFS)[6]表示。IVIFS是对IFS的扩展，在模糊不确定信息的表达和处理方面更具有实用性。王坚强[7]给出了一种权系数信息不完全确定的区间直觉模糊决策方法，徐泽水[8]提出新的IVIFS的得分函数和精确函数，并应用到区间直觉模糊MADM领域，卫贵武[9]将经典的TOPSIS决策方法扩展到区间直觉模糊环境，高建伟等[10]基于前景理论给出了一种区间直觉模糊决策方法，邵良杉等[11]在区间直觉模糊信息下提出了双向投影决策方法。

考虑到实际决策过程中，受到环境的复杂和人的认知等因素的影响，决策者可能给出方案满足和不满足一个属性的程度之和大于1 的情况，例如：评价软件开发项目，对于技术可行性这个属性，决策者给出具有这个属性的程度为0.5，而不具有这个属性的程度可能为0.6，由于，直觉模糊数无法描述，但0.52+0.62=0.61<1为此，Yager提出了Pythagorean模糊集[12,13]其特点是隶属度与非隶属度之和可以大于1，但隶属度与非隶属的平方和小于等于1，可见Pythagorean模糊集是对直觉模糊集的一种扩展，因此，在处理模糊性和不确定性信息方面具有更强的表现能力。在Pythagorean模糊环境下，Zhang等[14]提出一种扩展的TOPSIS决策方法，Garg[15]提出了基于Einstein集结算子的MADM方法，Ren等[16]提出了Pythagorean模糊TODIM多属性决策方法，Zhang[17]提出了Pythagorean模糊层次QUALIFLEX决策方法，刘卫锋等[18]提出了一些广义Pythagorean模糊信息集结算子(PFOWA算子、GPFOWA算子、PFOWG算子、GPFOWG算子)并将其应用到的MADM领域。正如IVIFN是对IFN的扩展，区间Pythagorean模糊数(IVPFN)是对Pythagorean模糊数的扩展。Peng等[19]提出了扩展的区间Pythagorean模糊ELECTRE决策方法，Liang等[20]利用偏差最大化方法确定属性权重，并提出了基于区间Pythagorean模糊加权平均算子的决策方法。

以上文献研究表明，区间Pythagorean模糊MADM问题研究还有待完善。鉴于此，本文研究属性值为IVPFN，属性权重不完全确定的MADM问题。将相对熵与IVPFN结合，给出一种新的与理想方案的相对满意度，进而确定属性权重。提出一种新的IVPFN得分函数，据此确定每一个属性下方案间的优序关系及0-1优先关系矩阵，结合属性权重和AQM (Alternative Queuing Method)方法计算各方案的综合度，给出排序结果。最后，将此方法应用于软件开发项目的选择。

1 区间Pythagorean模糊数及相对熵

1.1 区间Pythagorean模糊数

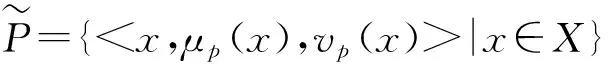
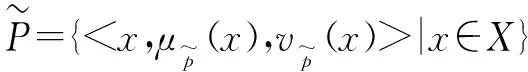
1.2 相对熵

相对熵可以描述两个系统的差别，设A,B为两个系统，它们的状态为xi和yi(i=1,2,…,l)，则两个系统之间相对熵[21](Kullback-Leibler距离)为

M(A(xi),B(xi))

(1)

相对熵不满足对称性，它不是两个系统间的真正距离。然而，将相对熵视为两个系统间的距离可以解决TOPSIS法无法克服两方案中垂线上点的排序问题[2]。在(1)式的基础上，下面给出IVPFN的相对熵。

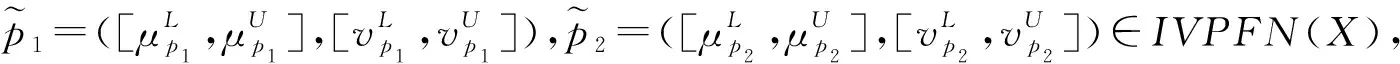
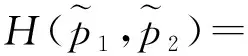
(2)

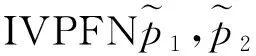
2 基于相对熵的区间Pythagorean模糊信息下AQM决策方法

2.1 决策问题描述

2.2 属性权重的确定

实际决策过程中，往往属性权重信息不完全已知。 借鉴TOPSIS思想，如果某个方案与正理想方案区别越小(或者与负理想方案区别越大)，则相应的权重就应该越大，反之则越小。由(2)式相对熵可视为两者之间的距离，因此，依据方案与区间Pythagorean模糊正理想方案的相对熵越小相应权重越大的思想来确定属性权重。

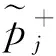
(3)

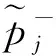
(4)

(5)

和

(6)

分别为方案Yi与Y+和Y-的加权相对熵。

H(Yi,Y+)反映了方案Yi与正理想方案Y+的差别，H(Yi,Y-)反映了方案Yi与负理想方案Y-的差别。由TOPSIS思想，某方案与正理想方案的相对熵越小，则该方案越优。记

(7)

为方案Yi的相对满意度。

相对满意度越大的方案应赋予越大的权重，反之亦然。为此，建立如下多目标优化模型

max (ξ1(ω),ξ2(ω),…,ξm(ω))

(8)

Ω为属性权重信息不完全的数学表达式集合。根据多目标优化理论，模型(8)可转化为如下单目标优化模型

(9)

模型(9)为有约束的非线性优化模型，由于目标函数的特点，传统的混合惩罚函数法或可行方向法均很难获得非劣解，可采用软件Matlab 7.0或Lingo 9.0求解获得权重。

2.3 区间Pythagorean模糊信息下的AQM决策方法

AQM方法是Navarrete等于1979年提出的一种决策方法，其核心思想是利用0-1优先关系矩阵给出方案的排序[22]。

在确定方案集{Y1,Y2,…,Ym}在每一属性下的0-1优先关系矩阵前，需要给出任意方案Yi与Yj的序。犹豫度也是IVPFN的重要指标，已有的IVPFN的得分函数[19]没有考虑犹豫度的影响，为此考虑犹豫度对排序的影响，提出一种新的IVPFN得分函数。

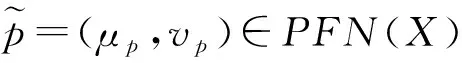
(10)

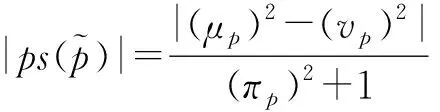
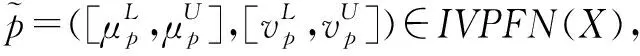
(11)

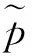
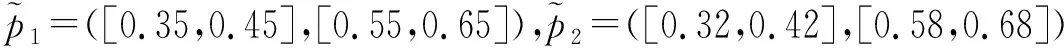
利用式(11)得分函数，可构造方案间的0-1优先关系矩阵D=(dij)m×m，如果Yi≻Yj，那么dij=1，且dji=0；如果Yi≈Yj，那么dij=dji=1；如果Yi与Yj不能比较，那么dij=dji=0。 于是，区间Pythagorean模糊信息下AQM决策步骤如下：

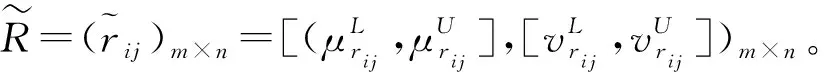
步骤3依据式(2)至式(9)确定属性权重ω=(ω1,ω2,…,ωn)T。

步骤4计算每一属性下方案Yi优于Yj、Yj优于Yi以及Yi与Yj无差别的权重：

对于方案Yi与Yj，在第k(k=1,2,…,n)个属性下，令(Yi≻Yj)k表示方案Yi优于Yj，令(YiYj)k表示方案Yj优于Yi，令(Yi≈Yj)k表示方案Yi与Yj无差异。由下式计算方案Yi优于Yj的权重：

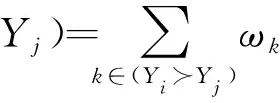
(12)

类似的方法可计算方案Yj优于Yi的权重ω(YiYj)和方案Yi与Yj无差异的权重ω(Yi≈Yj)。

步骤5计算所有方案对(Yi,Yj)的总体指示值

(13)

其中，σ表示Yi与Yj的重要度，且σ∈[0,1]。

步骤6给定阈值ε>1，计算方案{Y1,Y2,…,Ym}在所有属性下的总序关系

(14)

由式(14)得到所有属性下方案间的合成0-1优先关系矩阵D=(dij)m×m。

步骤7根据合成0-1优先关系矩阵D=(dij)m×m计算每个方案Yi(i=1,2,…,m)的综合度

λi=ρi-θi

(15)

其中，ρi为D=(dij)m×m的第i行元素为1的个数，θi为第i行元素为0的个数。综合度λi的值越大，方案Yi(i=1,2,…,m)越优，依据λi得到所有方案的排序，从而得到最佳方案。

3 实例分析

步骤1区间Pythagorean模糊决策矩阵如表1所示。

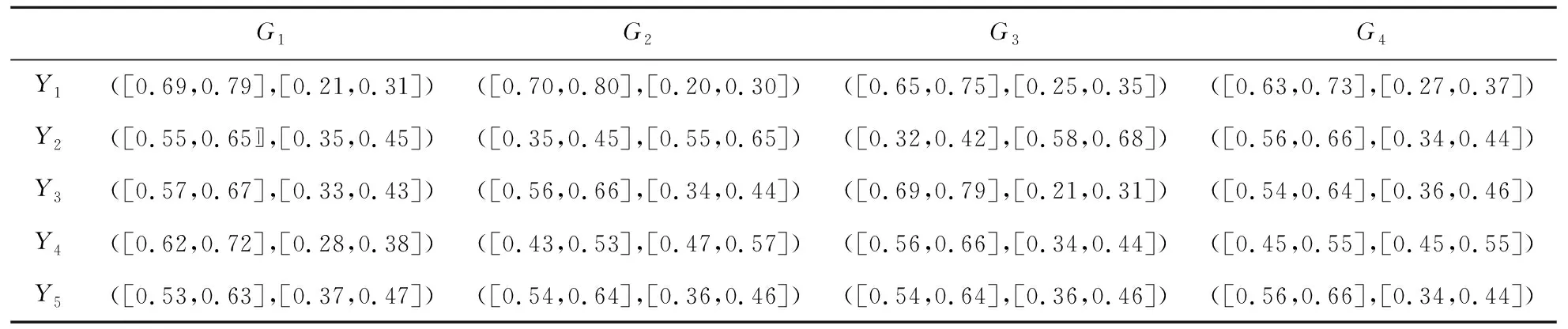
表1 区间Pythagorean模糊决策矩阵

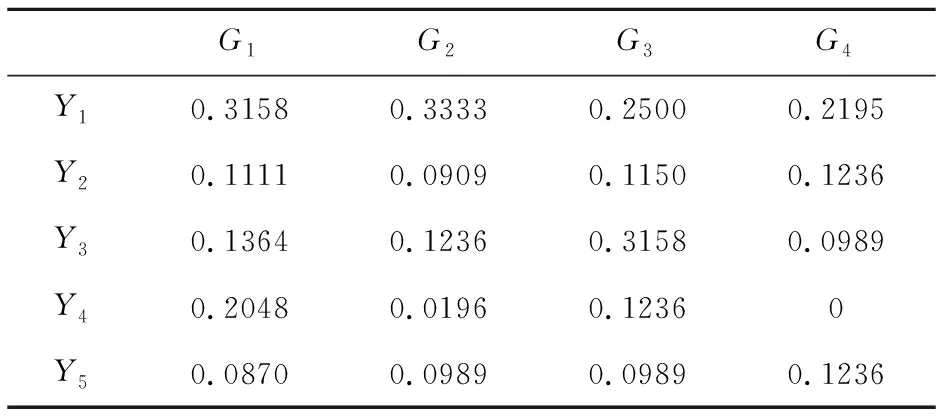
表2 得分函数矩阵

步骤2利用式(11)计算得分函数矩阵，如表2所示。

根据表2计算属性Gj下方案{Y1,Y2,…,Y5}间的0-1优先关系矩阵Dj=(dkl)5×5(j=1,2,…,4),结果如下：

步骤3利用表1的数据，构建形如式(9)模型，利用软件Matlab 7.0求得属性权重ω=(0.30,0.22,0.25,0.23)T。

步骤4利用式(12)计算方案Yi优于Yj的权重ω(Yi≻Yj)，以及权重ω(YiYj)和ω(Yi≈Yj)，结果如表3所示：

表3 方案间的序及对应的权重

步骤5利用式(13)计算所有方案对(Yi,Yj)的总体指示值(取σ=0.5)，如表4所示：

表4 σ=0.5时的总体指示值

步骤6利用式(14)计算(取ε=1.11)所有方案间的合成0-1优先关系矩阵D=(dij)5×5。

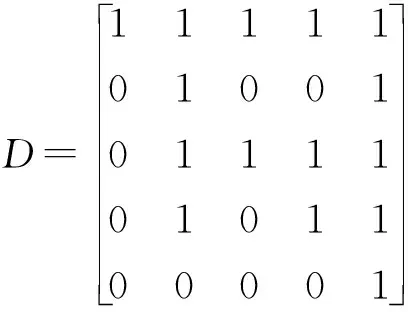
步骤7根据式(15)计算每个方案的综合度：λ1=5,λ2=-1,λ3=3,λ4=1,λ5=-3,由此可知，λ1>λ3>λ4>λ2>λ5,即方案排序结果为：Y1≻Y3≻Y4≻Y2≻Y5，表明电子邮件开发项目Y1为最佳选择。

为了分析决策过程中参数重要度σ和阈值ε对决策结果的影响，分别取(σ,ε)=(0,1.1),(0.2,1.1),(0.4,1.4),(0.6,1.6),(0.8,1.8),(1.0,2.0),通过计算方案的综合度，并将综合度和排序结果列入表5，如表5所示。

表5 6种参数组合下各方案的综合度和排序结果

由此可知：

(1)按照文献[20]中的区间Pythagorean模糊加权平均算子(IVPF-WAA)，假设属性权重为ω=(0.30,0.20,0.25,0.23)T，并利用得分函数得到排序结果：Y1≻Y3≻Y4≻Y2≻Y5, 与表5中当参数(σ,ε)=(0,1.1),(0.2,1.1),(0.4,1.4)时完全一致，说明本文的决策方法是合理可行的；

(2)按照文献[19]中的ELECTRE方法,得到的排序结果：Y1≻Y3≻Y4≻Y5≻Y2，与本文的排序结果略有不同，但最佳选择都是项目Y1。其原因，文献[19]是在属性权重信息完全未知情形下，利用距离测度构建偏差最大化模型求解权重，而本文是在属性权重信息不完全已知情形下，利用相对熵测度构建相对满意度最大化模型求解权重，同时也说明参数(σ,ε)的变化对决策结果具有重要影响。

4 结论

本文研究了属性权重不完全确定的区间Pythagorean模糊多属性决策问题，提出了IVPFN的相对熵、区间Pythagorean模糊正理想方案及区间Pythagorean模糊负理想方案的概念，依据方案与区间Pythagorean模糊正理想的相对熵越小权重越大的原则，建立了基于方案相对满意度优化模型，以此获得属性权重；接着，提出了一种新的IVPFN得分函数，据此获得了方案间的序关系以及每一个属性下方案间的0-1优先关系矩阵，进一步，对经典AQM决策方法进行扩展得到方案间的合成0-1优先关系矩阵，依据方案的综合度获得了方案的排序结果。最后用实例说明了该方法的有效性和可行性。