需求不确定下供应链间古诺博弈决策分析

孙红霞, 李 煜, 李继华

(1.北京工商大学 商学院,北京 100048; 2.国网北京市电力公司 物资分公司,北京 100054; 3.山东华宇工学院 基础部，山东 253034)

0 引言

现如今，为了能在日趋激烈的市场环境中获取竞争优势，企业间单打独斗的竞争模式已十分罕见，取而代之的是供应链与供应链之间的竞争模式。企业往往通过采取与供应链上下游企业紧密合作的方式参与市场竞争，在实现“单赢”的同时实现“共赢”，从而为企业带来更多的利润。然而在供应链间的竞争中，各供应链上的成员是以最大化供应链整体利润为目标进行决策还是以最大化自身利润为目标进行决策都是需要考虑的问题。所以，如何为企业确定最佳决策结构，如何制定合理的产品价格从而使供应链获得更多竞争优势，是企业在供应链管理中需要解决的关键问题。因此，开展供应链间竞争决策分析研究对于指导供应链的实际运营有着重要的现实意义。

目前有关供应链竞争决策的研究主要集中于两个方面。一方面是以单条供应链为研究对象，分析供应链内部的不同企业间的竞争问题[1～6]。另一方面则是考虑供应链与供应链间的竞争。肖迪和黄培清[7]采用非合作博弈的方法研究了两条均由一个供应商和一个制造商组成的供应链之间的价格竞争。李伯勋等[8]以两条包含一个制造商和一个零售商的供应链为研究对象，讨论了两供应链采用不同决策结构时链间Stackelberg博弈问题。孟庆春和李慧慧[9]通过考虑供应链间的竞争关系，结合新产销合一理念，研究了供应链价值最大化问题。不少学者还将供应链间的竞争应用于不同领域。陈志松等[10]研究了多晶硅光伏供应链的竞争、合作与协调。付小勇等[11]将双链竞争问题用于解决废旧电子产品回收市场中存在处理商选择回收渠道的问题，并构建了双链竞争下处理商回收渠道选择的博弈模型。Hafezalkotob[12]将链间价格竞争问题拓展到绿色供应链中，建立了在政府财政干预影响下的价格竞争模型。此外，一些学者还研究了需求不确定环境下的供应链竞争的问题。Wu等[13]研究了在需求不确定下两条供应链竞争的均衡解。艾兴政等[14]利用贝叶斯统计推断方法和博弈理论构建市场不确定环境下链与链竞争的控制结构模型。之后，艾兴政等[15]又构建了在需求不确定环境下两个制造商、两个排他性零售商构成的链与链价格竞争模型。Ai等[16]研究了在需求不确定条件下两条销售可持续产品的供应链间的竞争问题，对制造商与零售商的决策进行分析。He等[17]分析了需求不确定环境下多条供应链间的竞争问题。张婷婷[18]利用均值标准差期望效益函数研究了不确定市场需求下零售商是领导者，制造商是跟随者的两条供应链间的价格竞争。

近年来，随着人们所研究问题复杂性和不确定性的提高，对模糊集理论的研究也越来越丰富。主要对区间值模糊集[19]、直觉模糊集[20]和区间值直觉模糊集[21]等进行研究，并将这些模糊集理论拓展到理论研究、解决多属性决策问题和实际应用中。由于市场信息的不确定性以及决策环境的复杂性，对市场需求函数的变动情况的认识是模糊的，很难用精确的数据对市场需求函数进行描述，而模糊集理论恰好可以提供一种处理市场需求函数模糊性的方法。在上述文献中研究的需求不确定供应链间竞争问题中，未将决策者的态度或偏好考虑其中。而在现实中，决策者的态度在供应链管理中起着至关重要的作用，会影响最终的决策结果，所以有必要将决策者对供应链风险的态度考虑其中。因此，本文利用区间数将需求函数模糊化，并引入心态指标用于描述决策者对风险的态度，构建了三种模式下的供应链间价格竞争模型，分析了心态指标等变量对零售价格、顾客需求量、供应链利润以及最终决策结果的影响。

1 区间数及其排序

定义1[22]设A=[aL,aU]为有界闭区间，如果aL,aU∈,则称A为区间数，用I={[aL,aU]|aL≤aU,aL,aU∈}表示上的全体区间数。当aL=aU时，记[aL,aU]=aL，即实数可视为特殊的区间数。

定义2[22]设A=[aL,aU]，B=[bL,bU],A,B∈I且aL>0,bL>0，定义运算如下：

(1)[aL,aU]+[bL,bU]=[aL+bL,aU+bU]；

(2)[aL,aU]-[bL,bU]=[aL-bU,aU-bL]；

(3)λ×[aL,aU]=[λaL,λaU]，λ>0。

定义3[23]设区间数A=[aL,aU]，对任意的α∈[0,1]，其排序指标定义如下：

FA(α)=MA+(2α-1)DA

(1)

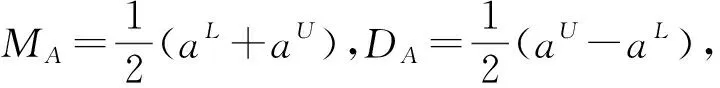
对任意两个区间数A=[aL,aU]和B=[bL,bU]，排序方法如下[23]：

(1)若任意α∈[0,1]，均有FA(α)≤FB(α)，则A≤B；

(2)若任意α∈[0,1]，均有FA(α)=FB(α)，则A=B；

(3)若任意α∈[0,r]⊂[0,1]有FA(α)≤FB(α)，而任意α∈[r,1]⊂[0,1]有FA(α)≥FB(α)，对于心态偏谨慎者而言，A≤B；对于心态偏激进者而言，A≥B。

2 问题描述

本文考虑市场上存在两条包含一个制造商和一个零售商的二级供应链。假设两条供应链经营可相互替代的同质商品，供应链间进行古诺博弈，供应链内部进行Stackelberg博弈，目标是选择价格策略并最大化利润。此外，根据供应链采用集中决策还是分散决策，链间博弈中产生了三种决策结构，即分散-分散决策、集中-分散决策和集中-集中决策。其中，集中决策是以最大化供应链整体利润为目标进行决策；分散决策是以最大化自身利润为目标进行决策。

为了方便讨论与分析，本文首先给出如下记号：

dik：需求不确定下第k种模式第i条供应链的顾客需求量；ai：需求不确定下第i条供应链的市场规模，它描述的是当零售价为零时的需求；b：需求不确定下顾客需求对价格的敏感系数；θ：需求不确定下产品的可替代性；pik：第k种模式下零售商i的零售价格；wik：第k种模式下制造商i的批发价格；ci：制造商i的单位生产成本；πRik：需求不确定下第k种模式零售商i的利润函数；πMik：需求不确定下第k种模式制造商i的利润函数；πSCik：需求不确定下第k种模式供应链i的总利润函数。

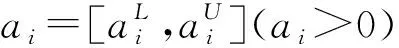
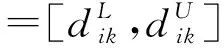
i=1,2;j=3-i

(2)

零售商的利润函数可表示为

πRik=(pik-wik)×dik

(3)

制造商的利润函数可表示为

πMik=(wik-ci)×dik

(4)

供应链的总利润函数可表示为

πSCik=(pik-ci)×dik

(5)

根据公式(1)，零售商、制造商以及供应链总利润函数的排序指标可依次表示为

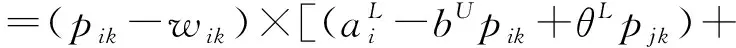
(6)

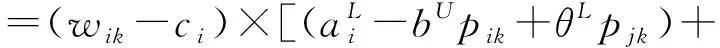
(7)

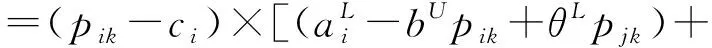
(8)

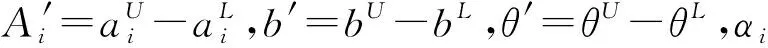
注1平均心态指标是指第i条供应链上各成员心态指标的平均数。即αi=(αi1+αi2)/2，其中αi1为第i条供应链上制造商的心态指标；αi2为第i条供应链上零售商的心态指标。

注2由于利润函数为区间数，而区间数的排序由排序指标的大小决定。因此，最大化利润通过最大化排序指标来实现。

3 模型建立与分析

在建立供应链间价格竞争模型时，假设供应链中的产销量相等，因为两条供应链进行的是古诺博弈，因此他们同时决定各自的零售价格和批发价格。在进行分散决策时，供应链中的制造商为领导者，零售商为跟随者，即链内进行的是Stackelberg博弈。下面将对分散-分散决策(模式1)、集中-分散决策(模式2)和集中-集中决策(模式3)这三种情况分别建立模型并求解。

3.1 模式1：分散-分散决策

在该模式下，两条供应链均采用分散决策，根据假设，存在链内动态博弈。首先，制造商i以利润最大化(即最大化利润的排序指标，下文不再赘述)为目标确定批发价格wi1即：

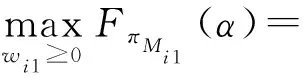
其次，零售商i根据制造商i的批发价格wi1来确定零售价格pi1并使自身利润最大化，即：

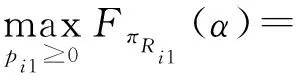
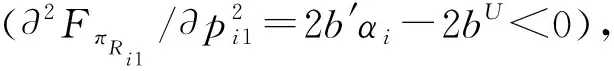
(9)

联立p11与p21得

(10)

将式(10)代入式(7)，求wi1偏导，得到制造商的批发价格wi1，即：

(11)

根据公式(11)可得到分散-分散决策模式下批发价格的均衡解

(12)

再将公式(12)代入公式(10)可得到分散-分散决策模式下零售价格的均衡解

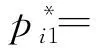
(13)

最后，将公式(13)分别代入公式(2)和(5)，可求得分散-分散决策下的顾客需求量和利润函数。

3.2 模式2：集中-分散决策

集中-分散决策表示第一条供应链采用集中决策，以最大化供应链整体利润为目标决策；而第二条供应链采用分散决策。

首先分析第一条供应链。由于该链采用集中决策，则有

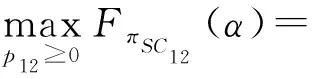
由∂FπSC12/∂p12=0，得到

(14)

其次分析第二条供应链。第二条供应链内进行Stackelberg博弈，即：制造商作为领导者先给出批发价格，零售商根据给定的批发价格做出最优反应，根据公式(6)，采用逆向归纳法得到零售商2的零售价格

(15)

联立公式(14)和(15)，得到

(16)

(17)

将公式(16)(17)代入公式(7)，并对w22求偏导，得到供应链2批发价格的均衡解

(18)

将公式(18)分别代入公式(16)(17)，可得到集中-分散决策模式下零售价格的均衡解

(19)

(20)

最后，将公式(19)(20)分别代入公式(2)和(5)，可求得集中-分散决策下的顾客需求量和利润函数。

3.3 模式3：集中-集中决策

当两条供应链都采用集中决策时，两者均以最大化供应链整体利润为目标进行决策，并确定最优的零售价格，即:

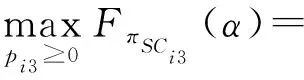
由∂FπSCi3/∂pi3=0，得到

(21)

联立p13与p23可求得集中-集中决策模式下零售价格的均衡解

(22)

最后，将公式(22)分别代入公式(2)和(5)，可求得集中-集中决策下的顾客需求量和利润函数。

3.4 结果分析

性质1在分散-分散、集中-分散和集中-集中三种竞争模式下，两条供应链上的零售价格均随着市场规模的扩大而增大。

证明将公式(13)(19)(20)(22)对Ci求偏导，可分别得到

由于一阶导数均大于0，因此在这三种模式下零售价格随着市场规模的扩大而增大。

性质2在集中-分散和集中-集中竞争模式下，顾客需求量和供应链利润均随者市场规模的扩大而增大。

证明首先分析市场规模对顾客需求量的影响。将公式(19)(20)(22)代入(1)(2)两式并对Ci求偏导，可分别得到

将式子简化可得一阶导数大于0，因此在这两种模式下顾客需求量均随市场规模的扩大而增大。

同理，分别将两种模式下的供应链利润对求Ci偏导，可得供应链利润随着市场规模的扩大而增大。

性质3在集中-分散和集中-集中竞争模式下，两条供应链上的零售价格均随着产品可替代性的变大而增大。

证明将公式(19)(20)(22)对Mi求偏导，可分别得到

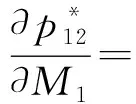
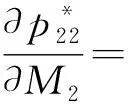
其中，S=4B1B2-M1M2。简化上述式子并发现其一阶导数均大于0，因此在这三种模式下零售价格随产品可替代性的变大而增大。

4 算例分析

考虑到模型的复杂性，本节在数值算例的基础上，分析了三种模式(分散-分散、集中-分散、集中-集中)下心态指标、产品可替代性、价格敏感系数、市场规模等关键变量对均衡解和最终决策结果的影响。为了重点讨论关键变量的影响，本节采用控制变量的思想假设两条供应链具有相似性，即α1=α2=α，c1=c2=c，a1=a2=a。

4.1 数值算例

假设市场上存在两条包含一个制造商和一个零售商的二级供应链，分别记为供应链1和供应链2，两条供应链上分别有制造商1、零售商1和制造商2、零售商2，他们经营着相互替代的同质商品，并在市场上进行价格竞争。假设两条供应链的单位生产成本和市场规模相同并且两条链上的决策者对供应链风险的态度持温和心态，在需求不确定环境下市场规模为a1=a2=[50,60]，产品可替代性为θ=[0.4,0.5]，顾客需求对价格的敏感系数为b=[0.6,0.7]，两条供应链中各成员的心态指标均为0.5，即α1=α2=0.5，单位生产成本为c1=c2=8。

根据上节的推导结果，可分别求出三种模式下的最优零售价、批发价、顾客需求量以及供应链利润，如表1所示。(结果保留2位小数)

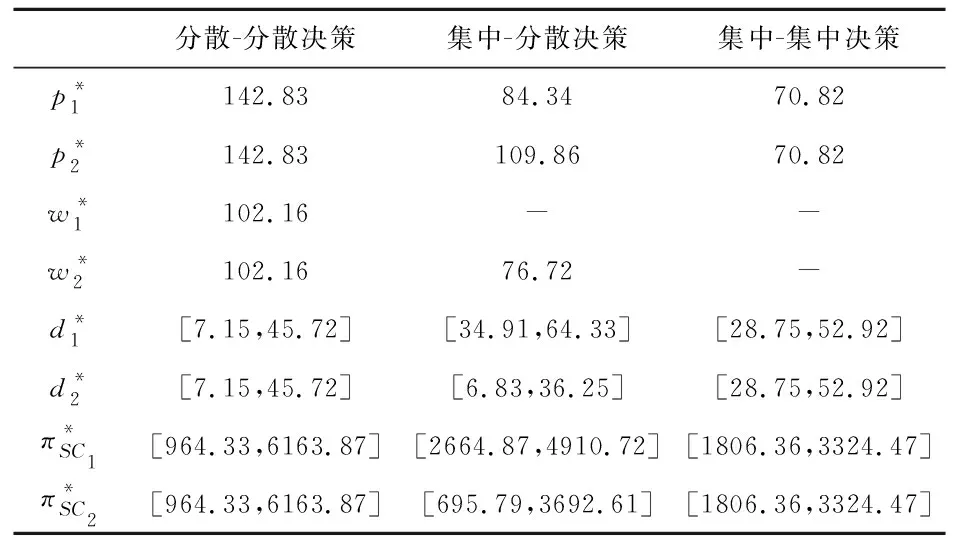
表1 三种模式下最优零售价、批发价、顾客需求量和供应链利润

4.2 心态指标对竞争结果的影响分析

心态指标反映了供应链上的决策者对风险的态度，风险的态度会影响到供应链间的竞争结果。基于上述例子，下面分析三种模式下心态指标的变化对零售价格、顾客需求量以及供应链利润的影响。图1、2、3分别反映了决策者的风险态度(α)与零售价格、顾客需求量和供应链利润的关系。以下各图中，集中-分散决策1代表采用模式2时第一条供应链的有关结果，集中-分散决策2代表采用模式2时第二条供应链的有关结果。

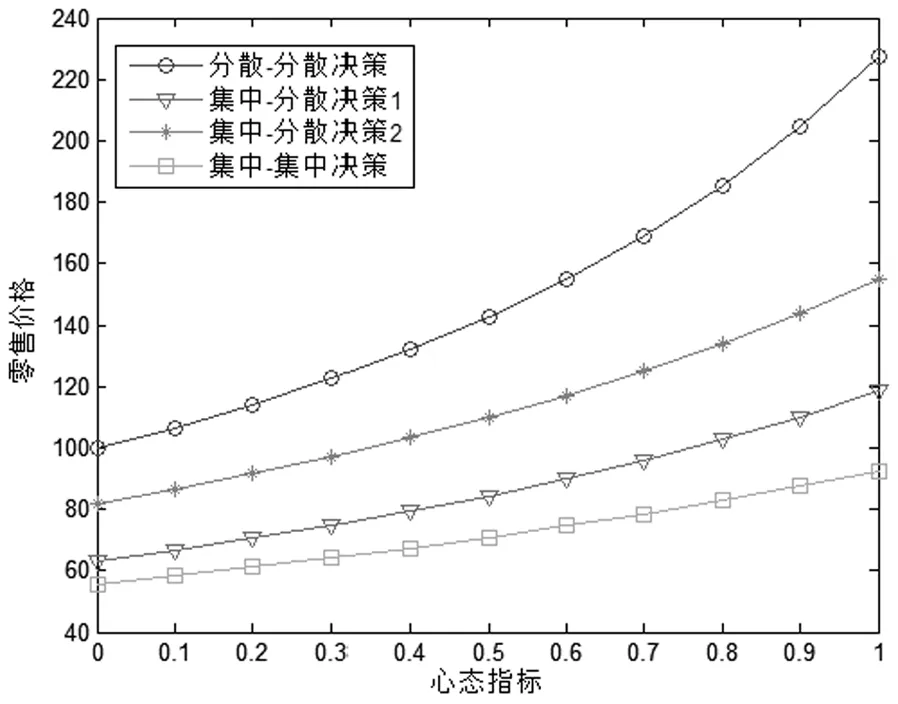
图1 不同模式下心态指标与零售价格的关系

在供应链竞争中，由图1可知，当决策者的心态逐渐趋向于乐观时，无论采取集中还是分散决策，零售价格都不断上升。此外，无论决策者的对待风险的态度如何，供应链间在进行价格竞争时，采取分散决策的零售价格要远高于采取集中决策时的情况，而且随着风险偏好的增加，采取分散决策的零售价格的增加速度大于采取集中决策时的情况。由图2可知，当决策者的心态逐渐趋向于乐观时，无论采取集中还是分散决策，顾客需求量都平稳上涨。其中，采取集中决策时供应链的需求量高于采取分散决策时的情况，当一条供应链采用集中决策而另一条采用分散决策时，采用集中决策的供应链需求量高的优势更明显。这说明采用集中决策的供应链利用较低的零售价格优势夺取了更多的市场，从而增加了自身的需求量。由图3可知，当决策者的心态逐渐趋向于乐观时，无论采取集中还是分散决策，供应链的利润都持续增长。当α≤0.7289时，无论其中一条供应链采取集中决策还是分散决策，另一条供应链采用集中决策要优于采用分散决策；当α>0.7289时，此时无均衡解。

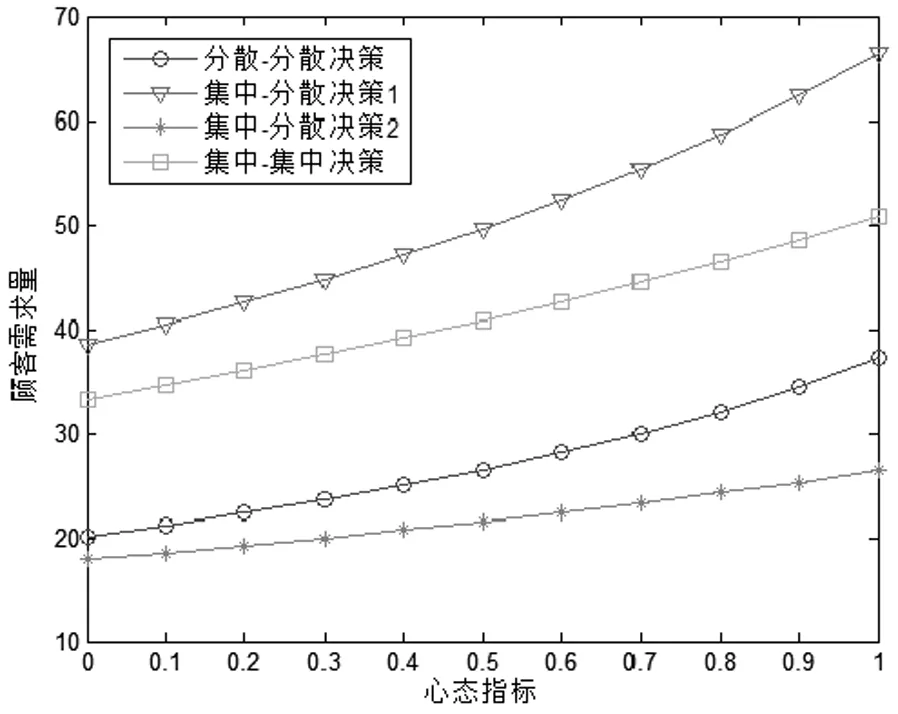
图2 不同模式下心态指标与顾客需求量的关系

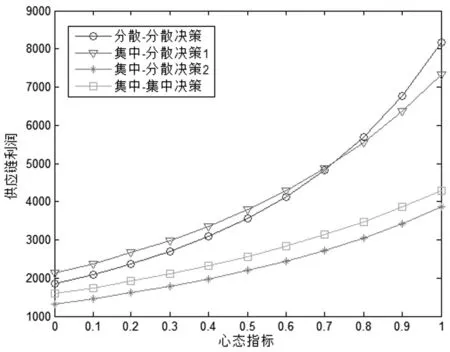
图3 不同模式下心态指标与供应链利润的关系

4.3 模糊变量对竞争决策结果的影响

基于上述分析，本节将讨论当模糊变量a,b,θ分别变化时，对决策结果的影响。假设模糊变量取值的左右端点差均保持0.1不变。

4.3.1θ改变对结果的影响

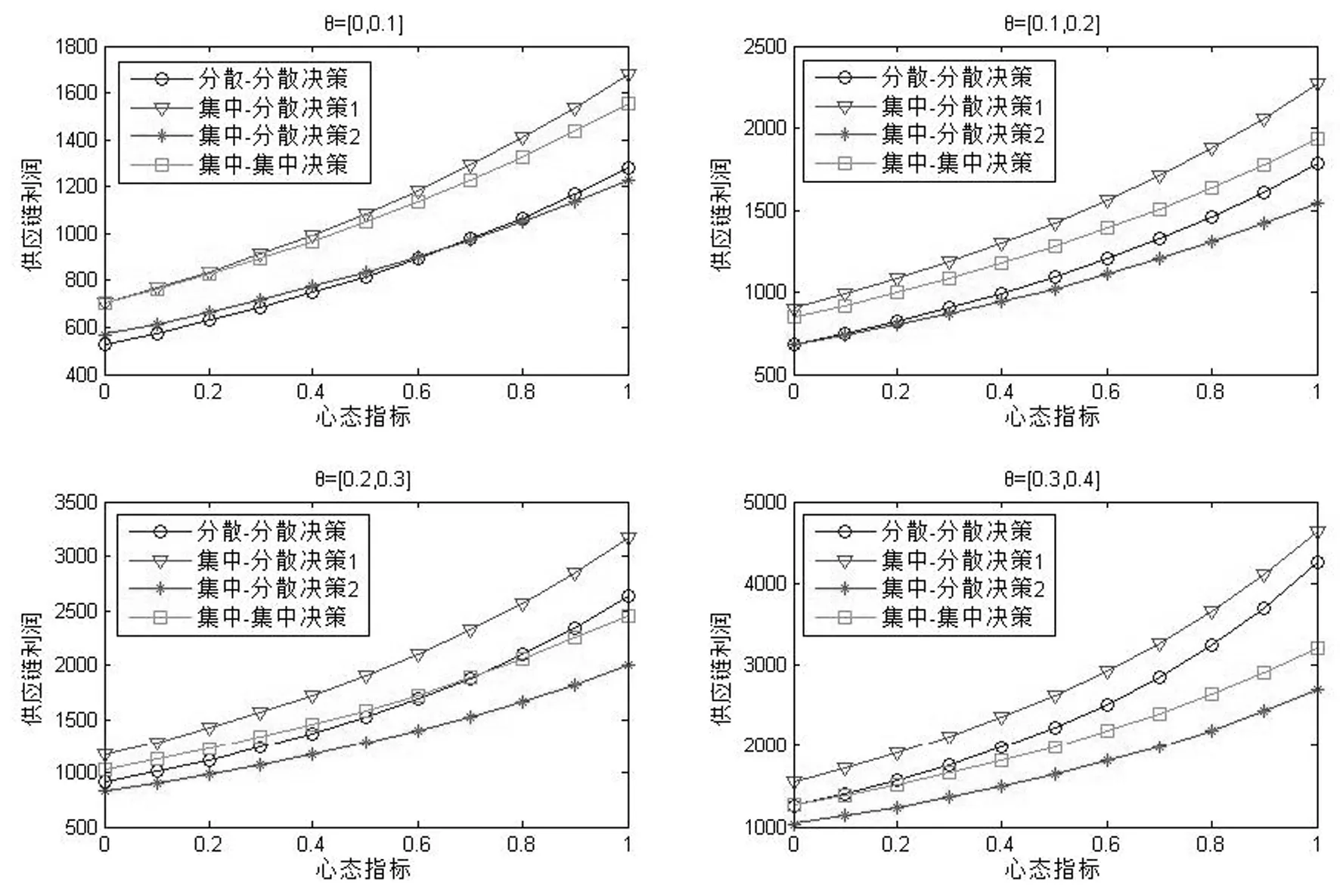
当θ分别等于θ=[0,0.1]，θ=[0.1,0.2]，θ=[0.2,0.3]，θ=[0.3,0.4]，且其他变量保持不变时，不同模式下供应链利润与心态指标的关系如图4所示。结合图3(θ=[0.4,0.5])，改变时五种决策结果见表2。

表2 不同θ下的决策结果

从结果来看，当决策者保持相同的风险态度时，相同模式下产品的可替代性越高，供应链的利润越高；当风险偏好的增加时，三种模式下的供应链利润均呈上升趋势。此外，产品的可替代性会影响最终的决策结果，当θ从[0,0.1]变化到[0.3,0.4]时，集中-集中决策为该供应链间竞争的唯一均衡解，且此决策结果不受心态指标的影响，而当θ=[0.4,0.5]时，决策的结果受心态指标的影响。分析发现，产品的可替代性越高，决策结果受心态指标影响的可能性会越大。

4.3.2b改变对结果的影响

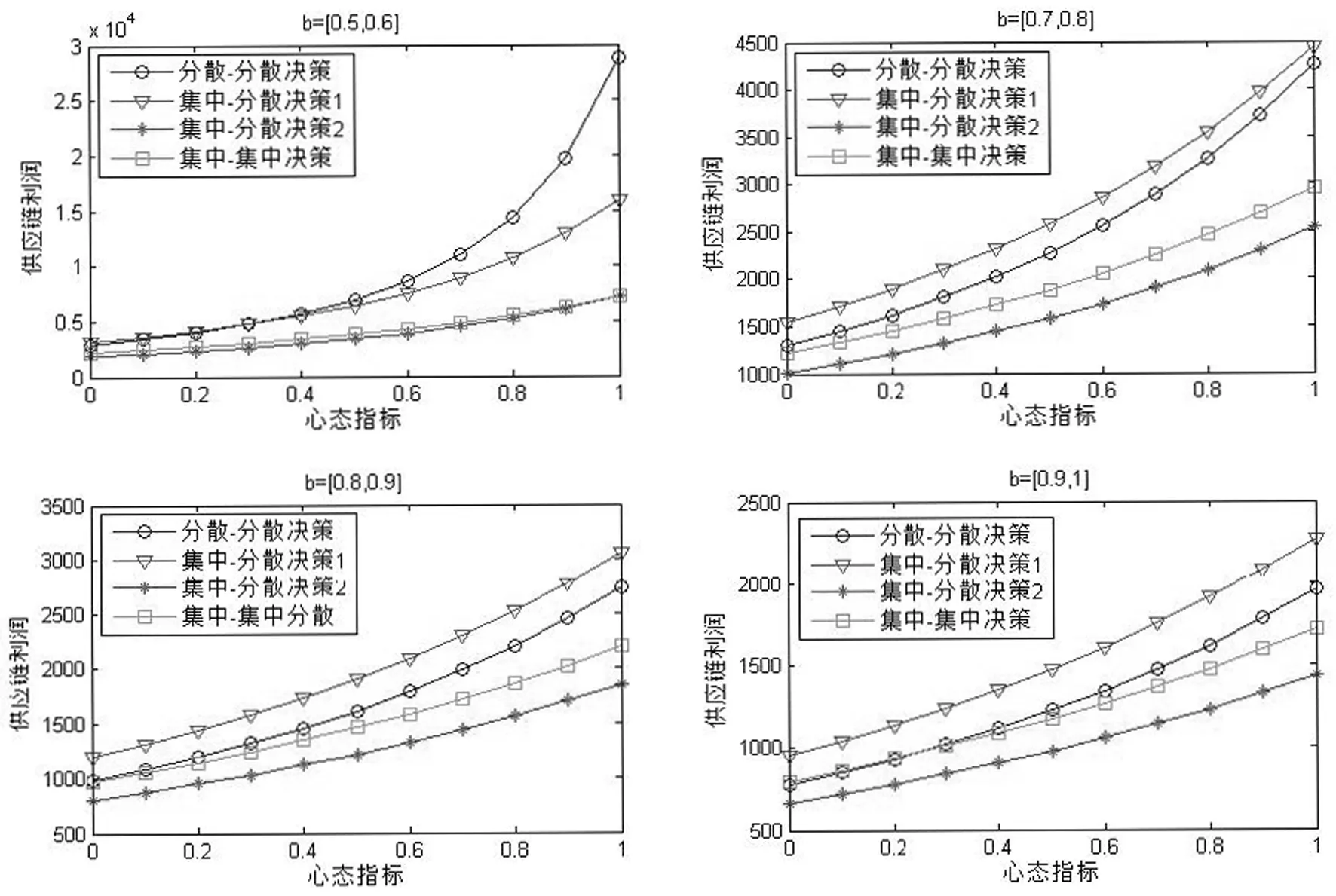
当b分别等于b=[0.5,0.6]，b=[0.7,0.8]，b=[0.8,0.9]，b=[0.9,1]，且其他变量保持不变时，不同模式下供应链利润与心态指标的关系如图5所示。结合图3(b=[0.6,0.7])，b改变时五种决策结果见表3。

表3 不同b下的决策结果

从结果来看，当决策者保持相同的风险态度时，相同模式下顾客需求对价格的敏感度越高，供应链的利润越低；当风险偏好的增加时，三种模式下的供应链利润均呈上升趋势。此外，价格敏感度不同对最终的决策结果会有影响，当b=[0.7,0.8]，b=[0.8,0.9]，b=[0.9,1]时，集中-集中决策为供应链间竞争的唯一均衡解，无论心态指标是多少，最终决策结果不变；而当b=[0.6,0.7]或b=[0.5,0.6]时，决策结果有了变化，并且不同的心态指标下的供应链利润会对最终决策结果有一定影响。分析发现，顾客的需求对价格的敏感度越低，决策结果受心态指标影响的可能性会越大。

4.3.3a改变对结果的影响

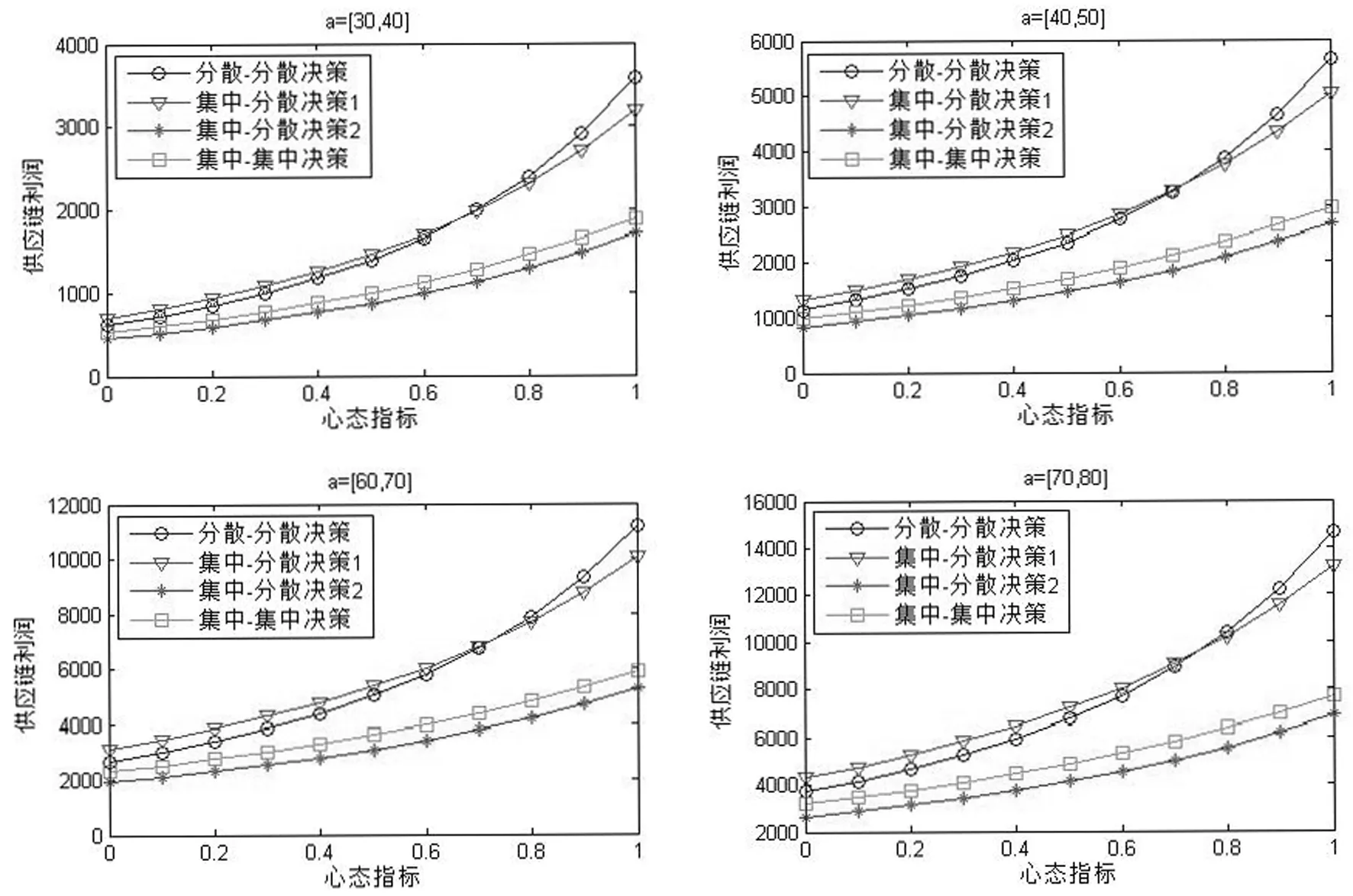
当a分别等于a=[30,40]，a=[40,50]，a=[60,70]，a=[70,80]，且其他变量保持不变时，不同模式下供应链利润与心态指标的关系如图6所示。结合图3(a=[50,60])，a改变时五种决策结果见表4。

表4 不同a下的决策结果

从结果来看，当决策者保持相同的风险态度时，相同模式下市场规模越大，供应链的利润越高；当风险偏好的增加时，三种模式下的供应链利润均呈上升趋势。此外，市场规模和心态指标的不同对最终的决策结果会有影响，随着市场规模的增大，获得均衡解所在的心态指标的范围也增大。分析发现，市场规模越大，决策结果受心态指标影响的可能性越小。

5 结论

本文研究了在需求不确定环境下两条包含一个制造商和一个零售商的二级供应链之间的价格竞争问题，考虑了链间竞争中产生的分散-分散决策、集中-分散决策、集中-集中决策这三种竞争模式。通过建立供应链间价格竞争模型求出不同模式下供应链竞争的均衡解，分析了需求不确定环境下市场规模对供应链利润、顾客需求量和零售价格的影响以及产品可替代性对零售价格的影响。通过算例分析出决策者对供应链的风险态度会影响零售价格、需求量、供应链利润以及最后的决策结果，分析发现市场规模越小，顾客的需求对价格的敏感度越低，产品的可替代性越高，决策结果受心态指标影响的可能性会越大。

在未来的研究中，可在本文的基础上将供应链上的一家制造商和零售商拓展为包含多家制造商与零售商的供应链；将两条链间的竞争拓展为多链间的竞争。此外，本文考虑的是链间同时竞争的情况，考虑链间竞争存在先后顺序，一条链为领导者，另一条链为跟随者的情形也是今后研究的方向。