素数和孪生素数判定方法①
2019-02-15周忠奇周师洁
佳木斯大学学报(自然科学版) 2019年1期
周忠奇, 周师洁
(1.湖北煤炭地质局,湖北 武汉 430070;2.北京新东方集团武汉学校,湖北 武汉 430070)
0 引 言
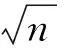
1 引 理
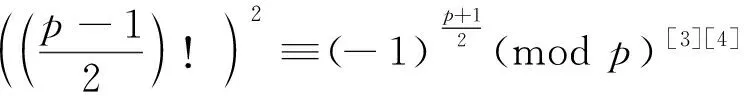
2 定 理
定理1: 奇数m为素数当且仅当
证: 必要条件:若m为素数,则
根据引理有
定理2: 设p≡1(mod 4),则p,p+2均为素数的充分必要条件是
证: 必要条件:若p,p+2皆为素数且p≡1(mod 4),根据定理1,有
又因p≡-2(modp+2),p2≡4(modp+2)和-5p≡10(modp+2)所以
根据定理1和p+2≡-1(mod 4)
由(1)和(2)得
必要条件成立.
因(p,8)=1,由(3)可得
根据定理1可知p为素数.再由(4)可得
因(p+2,2)=1,p+2≡-1(mod 4)所以
或
根据定理1知p+2为素数.充分条件成立.
定理3:设p≡-1(mod 4),则p,p+2均为素数的充分必要条件是
证: 必要条件:若p,p+2皆为素数,p≡-1(mod 4),根据定理1有
又因p≡-2(modp+2),p2≡4(modp+2)和5p≡-10(modp+2)所以
根据定理1和p+2≡1(mod 4)
由(5)和(6)得
必要条件成立.
因(p,8)=1,由(7)可得
根据定理1可知p为素数.再由(8)可得
因(p+2,2)=1,p+2≡1(mod 4),所以
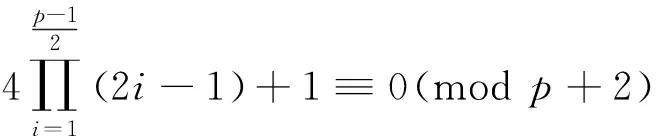
根据定理1知p+2为素数.充分条件成立.
3 结 语
以上素数和孪生素数的判定方法,只是对素数和孪生素数的一种刻画.由于这种判定方法都要计算所有不大于奇数m的连乘积的平方模m或模m(m+2),所以,这种判定方法在实际计算中不是高效率的.对于孪生素数,目前尚未发现有用一个式子且能在多项式时间内完成检测的方法.
