一类具有积分边界条件的分数阶微分方程的解①
2019-02-15孙园园周宗福
孙园园, 周宗福
(安徽大学数学科学学院,安徽 合肥 230601)
0 引 言
分数阶微分方程引起许多学者的研究兴趣,其中带有积分边值条件的分数阶微分方程出现很多研究工作。这些研究工作有些讨论的是分数阶微分方程边值问题解的存在性及唯一性,有些研究的是这类边值问题的正解。文献[5]讨论了带有积分边值条件的非线性分数阶微分方程解的存在性:
其中a∈C[0,1],b∈C([0,1],(-,0)),f∈C((0,1)×(0,+),[0,+)),g,h∈L1[0,1]为非负的,奇异点在t=0,1,u=0处。受到以上文献启发,研究下面具有双积分边界条件的分数阶微分方程
其中2<α为α阶Riemann-Liouville分数阶导数。分别用Banach压缩映像原理和Krasnoselskii不动点定理给出边值问题(1.1)解的存在唯一性及存在性。然后举一个例子说明定理的应用。
1 预备知识
定义1.1[7]函数f的α阶Riemann-Liouville分数阶导数定义为(α>0)
n-1α 引理1.2 假设y∈L1[0,1],2<α3,则下面带有双积分边值条件的分数阶微分方程 (2) 的解可表示为 其中 证对于(2),有 u(t)=c1tα-1+c2tα-2+c3tα-3- (3) 由条件u(0)=0,得c3=0。 又有 由条件可知 得 从而 (4) 易知,u(t)为方程(1.1)的解当且仅当u(t)为T的不动点。 定理2.1 假设f:[0,1]×R→R是连续函数且满足 (H1)存在常数l≥0,使得对任意t∈[0,1],x,y∈R有|f(t,x)-f(t,y)|l|x-y|; 那么边值问题(1)存在唯一解. 证令 Pb1={x∈E:‖x‖b1}。由(H2),易见b1>0,Pb1为E上的非空有界闭集。算子T如(4)所定义,下证TPb1⊂Pb1。对任意u∈Pb1,t∈[0,1]有 于是可得‖Tu‖b1,从而TPb1⊂Pb1。下面任取x,y∈Pb1,t∈[0,1],有 |(Tx-Ty)(t)||H(t,s)|‖x-y‖ds+ 故‖Tx-Ty‖由因此T为Pb1上的压缩映射。由Banach压缩映像原理,T在Pb1上存在唯一的不动点, 即边值问题(1.1)存在唯一解。 定理2.2 假设f:[0,1]×R→R连续,且满足以下条件 (H3)存在非负函数w1(s),w2(s)∈C[0,1],使得对任意(s,x)∈[0,1]×R,有 |f(s,x)|w1(s)|x|+w2(s) 那么边值问题(1)至少存在一个解。 又令Pb2={x∈E:‖x‖b2}。在Pb2上定义算子T1,T2: 由(H3),对任意x,y∈Pb2,t∈[0,1],有 |(T1x+T2y)(t)||H(t,s)|·|x(s)|ds+ w2(s))ds rb2+M1b2+M2 对任意x,y∈Pb2,t∈[0,1],有 由(H4)知,r<1,故T1为压缩映射。由f连续,则T2为连续算子。下证T2是全连续的。 |f(s,u(s))|w1(s)|u(s)|+w2(s) w1(s)‖u‖+w2(s)w1(s)b2+w2(s) 对任意u∈Pb2,t1,t2∈[0,1],不妨令t2>t1,则 |(T2u)(t2)-(T2u)(t1)|M|G(t2,s)- G(t1,s)|ds 由Arzela-Ascoli定理可知,T2Pb2为列紧的,从而T2在Pb2上是紧的。故T2在Pb2上全连续。 由Krasnoselskii不动点定理[8]可知,T=T1+T2在Pb2上至少存在一个不动点。因此, 边值问题(1)至少存在一个解。证毕。 例3.1 考虑下面的分数阶微分方程积分边值问题 (5) |f(t,u)|w1(t)|u|+w2(t),t∈[0,1] 故由定理2.2知,边值问题(5)至少存在一个解。 利用Banach压缩映像原理和Krasnoselskii不动点定理分析和研究一类带有双积分边界条件的分数阶微分方程,实际上还可以利用类似方法得到正解的存在性。
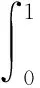
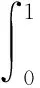
2 主要结果
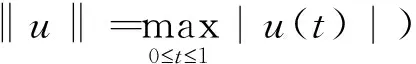
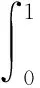
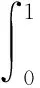

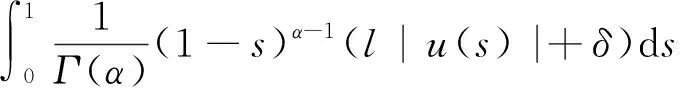
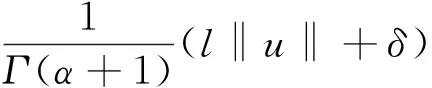


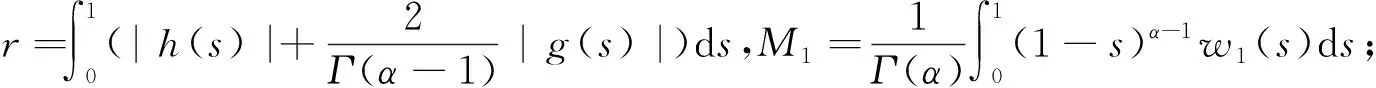
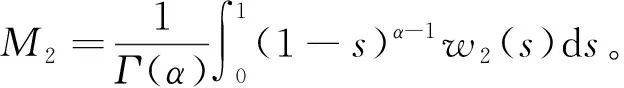



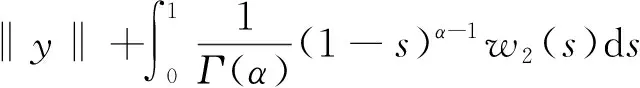
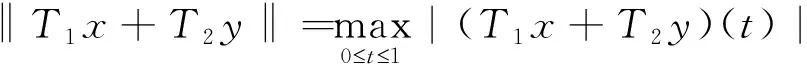
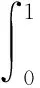

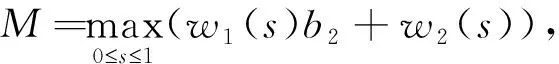

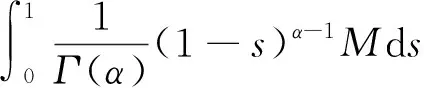
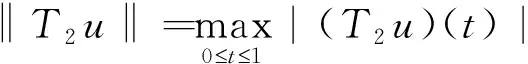
3 例 子
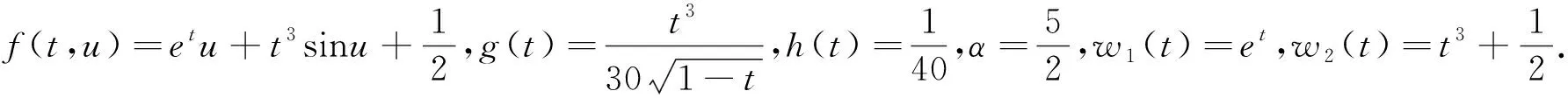
4 结 论
