零级Hamilton量二重简并的量子体系能级微扰法研究①

张伟欣， 韩海生， 李 颖， 张海丰

(佳木斯大学理学院，黑龙江 佳木斯 154007)

0 引 言

在量子力学中，体系的能量本征值能够精确求解的问题非常有限，除了少数体系(例如谐振子，氢原子等)外，往往不能严格求解[1]。因此，在处理各种实际问题时采用适当的近似解法，例如微扰论，变分法，自洽场方法，绝热近似，准经典近似等，其中最广泛的就是微扰论。

设量子力学体系的Hamilton算符为

H=H0+H′

(1)

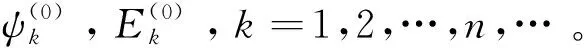
(2a)

(2b)

(2c)

(2d)

(2e)

等等。

设微扰作用后，能级和本征态变成

(3a)

ψn=ψ(0)+ψ(1)+ψ(2)+…

(3b)

零级近似ψ(0)由两个简并态ψα、ψβ组成：

ψ(0)=Cαψα+Cβψβ

(4)

规定波函数的各修正项和ψ(0)正交：

〈ψ(0)|ψ(1)〉=0

(5a)

〈ψ(0)|ψ(2)〉=0

(5b)

因此

(6)

将(3a)、(3b)代入能量本征方程

Hψn=(H0+H′)ψn=Enψn

(7)

并按能级分开，可得零级项

(8)

一级项

(9)

二级项

(11a)

(11b)

上式相当于{ψα，ψβ}子空间中H′的本征方程，即

(11c)

方程组(11)存在非平庸解的必要条件为

(12)

(13)

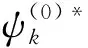
(14)

代入式(6)，即得

(15)

以ψ(0)*左乘式(10)，并对全空间积分，即得

(16)

讨论：

1)如在{ψα,ψβ}子空间中H′的对角元不相等，而非对角元为零，即

εα>εβ

(17a)

(17b)

这时式(13)给出

(18a)

(18b)

2)如果

εα=εβ=ε

(19)

(20)

这时式(13)给出

(21)

而式(11)给出

(22a)

(22b)

(22c)

(22d)

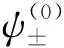
3)如果

(23)

2 给定H′取值的应用实例

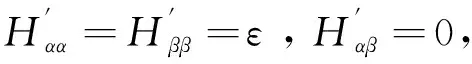
(24)

(25a)

(25b)

而上题式(14)代入式(25)，即得

(26a)

(26b)

存在非平庸的条件为Cα,Cβ的系数行列式等于0，即

(27)

其中

(28a)

(28b)

(28c)

讨论：

(29a)

(29b)

这些结果和非简并态微扰论的结果一样。

(30a)

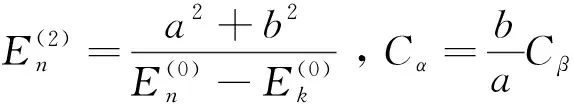
(30b)

3 结 论