任意角入射时matlab在电磁屏蔽材料设计中的应用①
2019-02-15韩海生张海丰裴魏魏
韩海生, 马 佳, 张海丰, 裴魏魏
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
随着信息技术的发展电磁屏蔽材料引起广大科研院所的高度重视,对抗与反对抗、电磁辐射污染、隐身技术、电磁能设备防干扰等引起了世界各国的高度重视,电磁屏蔽技术对国家国防事业发展和竞争力都起到了至关重要的作用[1~5]。多数论文对电磁波垂直入射界面进行分析研究,但由概率论原理垂直入射几率很小,只能作为电磁波斜入射的特例,电磁波斜入射的研究对工程材料优化设计、相关参数的匹配更具有重大意义[6~11]。论文利用全貌分析方法[12]的研究理念与三维网格法弥补某一电磁参数的影响所带来的负面效应,对电磁屏蔽材料的计算机辅助优化设计提供了理论支撑,三维网格法不仅提高材料外形设计的效率而且提高材料的吸收效果。
1 波密介质对后向反射率的影响
电磁波从波疏介质传到波密介质,在界面透射可以忽略不计,反射波存在半波损失,如图1所示,半波损失是引起能量损失的主要因素。
在界面处的入射波振动方程为y10,入射波振动方程为y20,由波的叠加原理可知位相差为π的奇数倍时,叠加后能量最小。波的反射与叠加原理和介质吸收系数为电磁屏蔽材料的后向反射率的设计提供了新的思路,当介质1足够薄时,后向反射率能达到最好效果。

图1 界面半波损失
(1)
y20=A20cos(ωt+φ20)
(2)
2 单层损耗材料的反射系数关系
由电磁波传输理论[13],线元dz可以看成集总参数电路,线元的电流与电压满足传输线方程:
(3)
(4)
求解式(3)与式(4),可得传输线的输入阻抗为
(5)
其中,Z1为介质1的输入阻抗,Z2为介质2的阻抗,d为介质的厚度。由传输线理论得出介质内电磁场的表达式为:
E2=E2y=(Aejα2z+Be-jα12z)ejσ2x
(6)
其中α2=k2z=k2cosθ2,σ2=k2x=k2sinθ2,k2为波数,θ2为入射角。
(7)
Zin=jZ2tgα2d2
(8)
可以看出有金属衬底的单层介质后向反射系数为
(9)
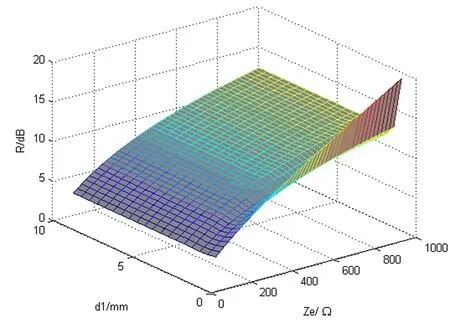
图2 斜入射时R与d、Ze的网格图
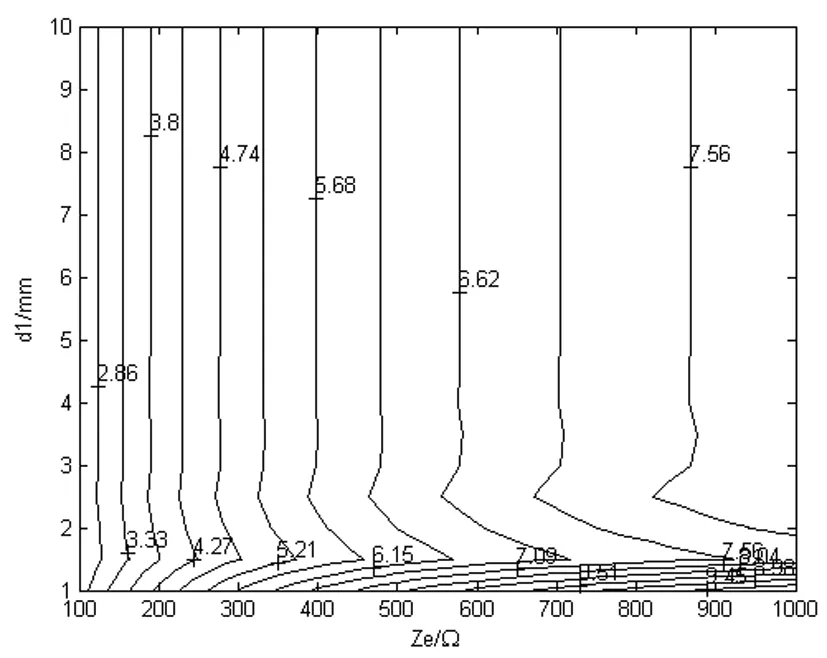
图3 斜入射时d与Ze的等高线
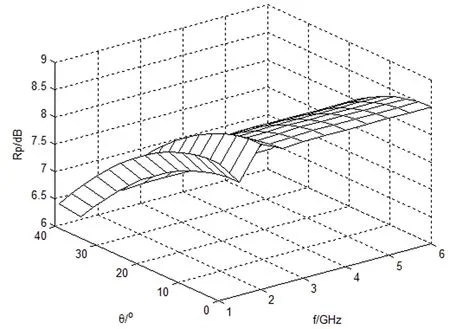
图4 斜入射时R与θ、f的网格图
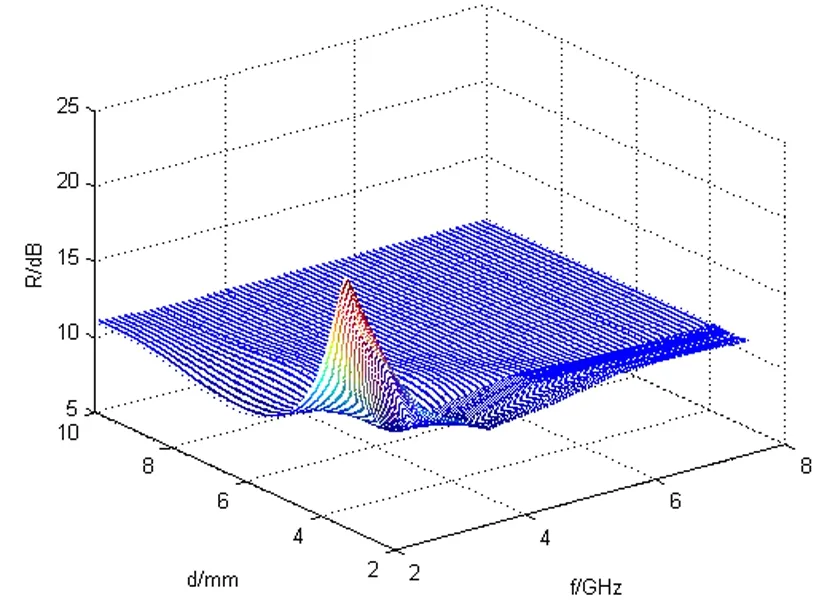
图5 斜入射时R与d、f的网格图
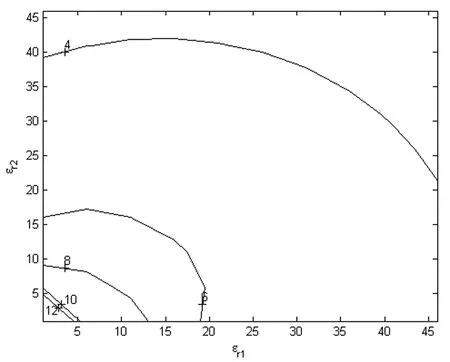
图6 斜入射时εr1和εr2的等高线

图7 斜入射时μr1和μr2的等高线
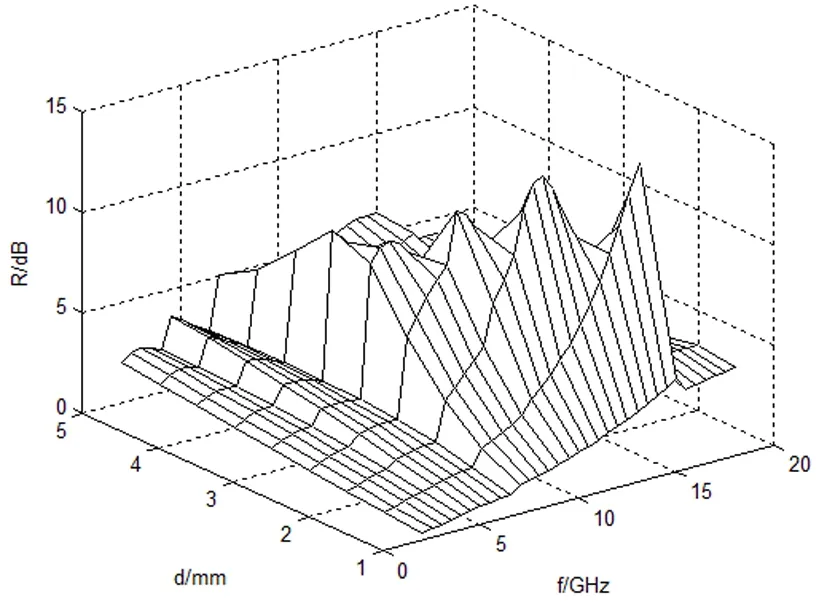
图8 有金属衬底的单层结构的R与f的关系式
3 利用网格法讨论参数对反射率的影响
从图2-图3可以看出,电磁屏蔽材料的后向反射率与屏蔽材料的厚度无关,随着阻抗值Ze的增加而增加,设计时通常只考虑阻抗值。
图4可以看出,后向反射率随入射角的增加而减小,但入射角在00~400时电磁屏蔽材料的后向反射率均大于6dB,满足设计要求。
图5可以看出在低频段曲线出现波动,高频段曲线平稳,在所有频段内,后向发射率达到10dB,满足工程设计的要求。
由参考文献[11-13]可知,随着介电常数εr1和εr2的增加,后向反射率的衰减dB值逐渐变小,后向反射率的衰减dB值随着磁导率μr1的μr2逐渐减小时,也随之变小;由图6可以看出εr1<18、εr2<16,μr>7后向反射率的衰减值均大于6dB,符合工程设计要求;
4 单层材料吸波特性的计算机辅助设计
电介质的极化与磁介质的磁化与频率息息相关,当入射波的频率增大时,极化与磁化现象减弱。根据利用三维网格法对盐酸参杂聚苯胺复合吸收剂在1-18GHz频段进行了优化设计,如图8所示。可以看出当考虑电介质与磁介质的频率特性时后发射率随着厚度的增加峰值向着低频段移动,且频带只是在窄频有较好的吸收效果。
5 结 论
吸波材料是通过能量转换实现对电磁波的有效吸收,衰减特性是利用半波损失与界面材料的阻抗匹配程度以及介质的吸收对电磁波进行衰减;文中利用三维网格法对影响后向发射率的电磁波的频率与入射角进行优化设计,设计结果表明当考虑频率特性时后向反射率与屏蔽膜的厚度相关,增加厚度可以提高低频段的吸收效果。
