速证“Goldbach猜想”
2019-02-15张奎福
数理化解题研究 2019年3期
张奎福
(吉林省长岭县巨宝中学 131533)
一、符号
p│mmmodp=0
p⊥mmmodp≠0
p∈Pp是质数
i∉Pi不是质数
n∈Nn是自然数
t在(a,b)区间a (a,b)区间跨度b-a ∏ 乘积 ∑ 求和 q∈P且(x-q)∈P时,q和(x-q)同是x的“1+1”,有D(x)个.如: D(1)=0;D(2)=0;D(3)=0;D(4)=1有2;D(5)=2有2,3;D(6)=1有3; D(7)=2有2,5;D(8)=2有3,5;D(9)=2有2,7;D(10)=3有3,5,7;D(11)=0. 偶数x>5时,D(x)>0, 即:大于5的偶数都有“1+1”. 设n∈N, ∵nmodp有p个可能值,且连续p个自然数n的nmodp互不同值, 设偶数x>5,2<奇数q 当恒有p⊥q(x-q)时,q∈P且(x-q)∈P, 当p⊥q(x-q)时, ∵p⊥q,∴qmodp≠0 modp. ③ ∵p⊥(x-q),∴qmodp≠xmodp. ④ 当p⊥x时,xmodp≠0 modp. 由①③④知:qmodp有(p-2)个可能值. ⑤ 当p│x时,xmodp=0 modp. 由①③④知:qmodp有(p-1)个可能值. ⑥ 又∵当(x-p)∈P时,p和(x-p)也是偶数x的2个“1+1”, ⑦ ∴由②⑤⑥⑦知: ∴有“1+1”定理:偶数x>5时,D(x)>0, 即:大于5的偶数都有“1+1”. “Goldbach猜想”成立.二、定义
三、猜想
四、准备
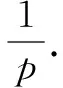
五、证明
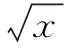

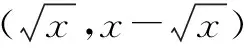
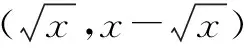
六、结论