基于改进应变能密度法的电动轮自卸车车架焊缝疲劳寿命预测

米承继 谷正气 蹇海根 张 勇 李文泰 余 冰

1.湖南工业大学机械工程学院，株洲，412007 2.长沙理工大学工程车辆轻量化与可靠性技术湖南省高校重点实验室，长沙，410114 3.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

电动轮自卸车是1 000万吨以上大型露天矿山场所运输的主力军，常年在矿山坑洼路面行驶，环境恶劣，工况复杂。车架作为最主要承载部件，其疲劳可靠性能是保证车辆正常作业和安全运行的关键因素。电动轮自卸车车架大多由高强度低合金调质中厚钢板拼焊而成，实际运行过程中往往在结构薄弱焊趾处发生开裂。由于车架结构几何形状复杂多变、截面尺寸大小和形式多样、载荷呈随机性且单个铰接位置受力达数十吨，损伤机理极其复杂，显然难以通过传统焊缝疲劳模型进行寿命理论计算或者利用疲劳试验来研究车架焊缝失效机理。因此，结合焊接接头微宏观性能试验和高精度理论模型进行数值模拟来研究电动轮自卸车车架焊缝疲劳可靠性问题很有必要。

焊缝失效的一种常见类型是焊趾处受垂直焊缝方向拉应力[1]，使焊趾处的缺陷发展，并最终导致结构失效。因而，求解焊缝的结构应力是进行损伤机理分析和疲劳寿命预测的关键因素。文献[2-4]利用线性外推法将结构应力表征为母材横截面内的拉应力和剪切应力，结合有限元法计算焊缝结构名义应力或热点应力。然而，对于复杂载荷作用下的焊缝结构应力数值计算大多强调结构在线弹性阶段的力学行为，这会忽略焊缝因为塑性变形而造成的疲劳损伤。文献[5]结合弹塑性力学理论和工程技术拓展临界平面法，提出利用非线性方程来描述临界平面内拉应力和剪切应力与拉应力疲劳极限和剪切应力疲劳极限，该方法能够预测焊缝的多轴比例和非比例循环加载疲劳寿命，但是对于复杂结构的工程实际问题至今仍然没有可靠的方法来高效确定临界平面的位置。为避开这一困扰，文献[6-8]通过焊缝结构的弹塑性力学模型求解应力应变响应，结合最大局部应力应变和应力应变疲劳寿命方程来评价剩余寿命，同时为保证数值求解计算精度，文献[9]还考虑焊缝的残余应力及热处理对焊接接头疲劳强度的影响，文献[10]提出利用三维激光扫描技术来构建焊缝精细化数值模型。然而，模型精度的提高并未从根本上解决焊缝寿命高精度预测问题。进而，文献[11-14]提出将弹塑性应变能量密度作为衡量焊缝疲劳损伤的参量，从能量转化角度揭示疲劳失效过程中焊缝损伤演化机理。

能量法与其他局部应力应变方法最大的区别在于，能量为一标量，能够有效避免矢量损伤参量所涉及的位置与方向问题。基于此，本文首先针对文献[12]构建的应变能量密度疲劳损伤模型进行改进，以拓展该模型对复杂载荷作用下材料或结构应力应变响应出现非完全封闭而交叉现象的表征能力。其次，开展高强钢焊接接头机械性能和疲劳试验研究，获取焊缝疲劳性能参数。再次，在电动轮自卸车车架有限元模型得到试验验证的基础上，开展多载荷步非线性有限元分析，根据数值计算得到的应力应变响应进行应变能量法疲劳寿命预测，并将预测结果和实际开裂位置进行对比分析。

1 应变能量密度法的改进

单一载荷循环作用下的结构应力应变响应一般为一完全封闭的曲线，其相应的弹性应变能密度和塑性应变能密度计算方法见图1。

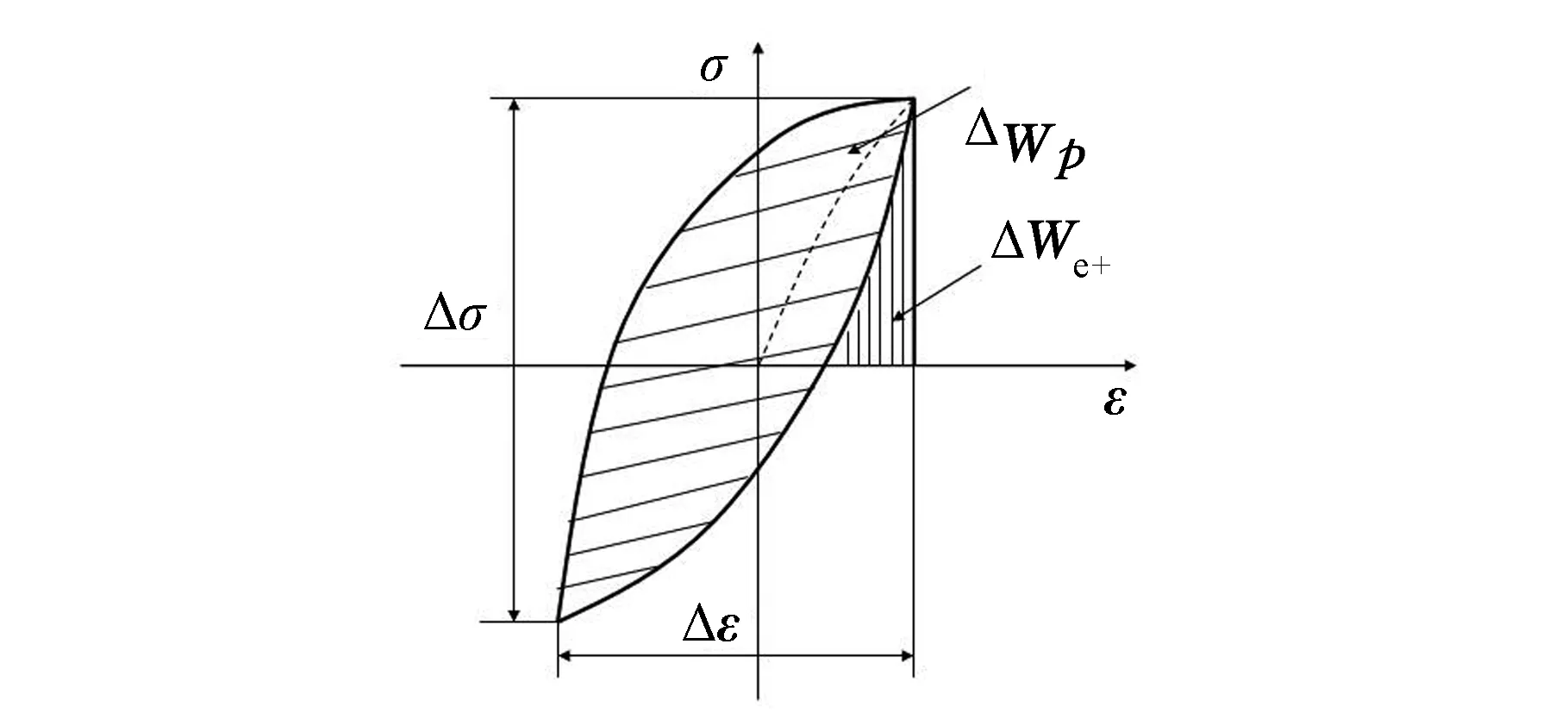
图1 单一载荷循环作用下应变能密度计算Fig.1 Strain energy density calculation under single loading

根据图1所示，当应力应变响应所围成的是一完全封闭的滞回曲线时，其拉伸正弹性应变能密度ΔWe+可表示为

(1)

为体现平均应力的影响，式(1)还可改写为

(2)

式中，σmax为拉伸最大应力值；E为弹性模量；Δσ为循环应力范围；σm为平均应力。

当材料承受压缩应力时，不会对疲劳损伤起作用，因而，不需要计算拉伸负弹性应变能密度。

单一载荷循环作用下的塑性应变能密度ΔWp可表示为

(3)

根据材料的循环应力应变本构方程，塑性应变能密度ΔWp可改写为

(4)

式中，Δεp为塑性应变范围；n′为应变硬化指数。

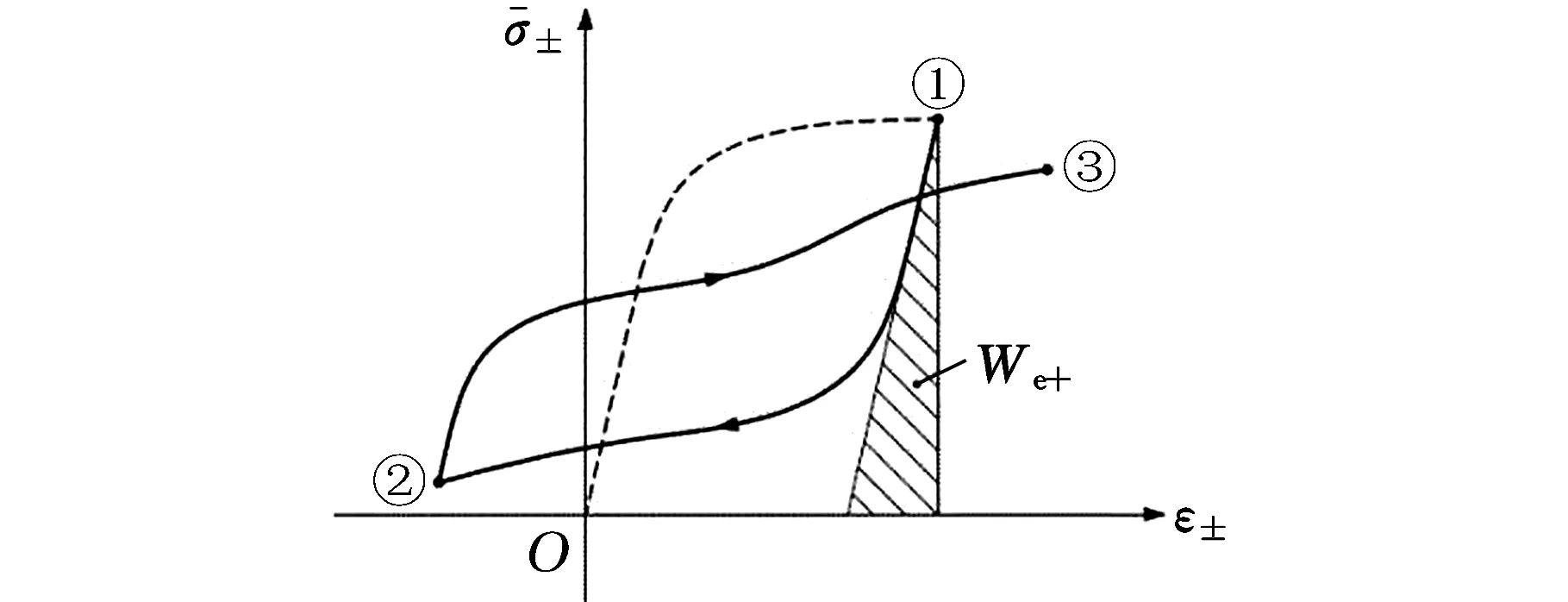
然而，对于实际焊接结构，往往会承受复杂的载荷作用，且在其循环加载作用下，焊缝会产生循环软化或硬化效应，使得应力应变响应发生相应的变化，以至于在载荷循环作用下出现应力应变曲线相交叉，呈现为一非完全封闭的曲线。为此，本文在已有的应变能密度求解方法上进行改进，将封闭环以外的部分塑性应变能密度也考虑进来，具体求解方法见图2。

根据图2所示，当应力应变响应所围成的是一非完全封闭的滞回曲线时，其拉伸正弹性应变能密度ΔWe+可表示为

(5)

(a)弹性应变能密度计算方法

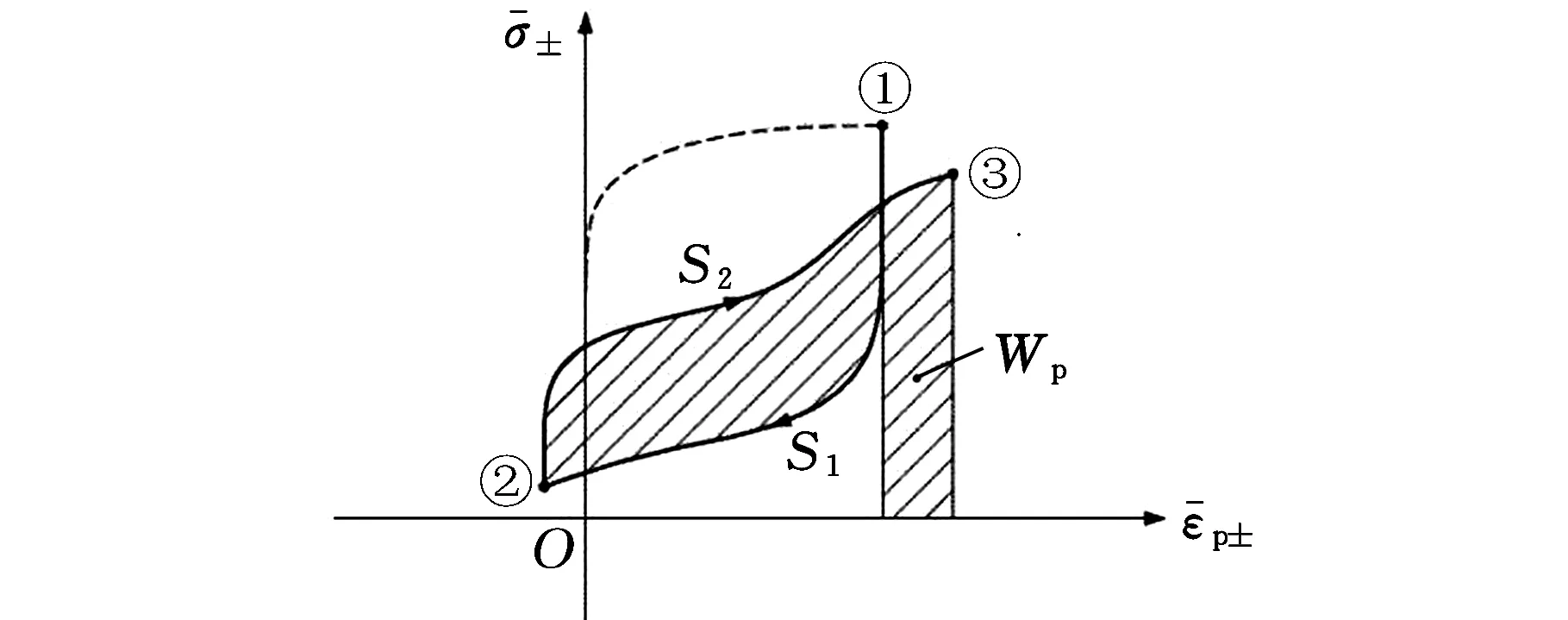
(b)塑性应变能密度计算方法图2 复杂载荷循环作用下应变能密度计算Fig.2 Strain energy density calculation undercomplex loading cycle

对于同样为非闭合的应力应变滞回曲线，塑性应变能密度可以由卸载和再加载所对应的面积组合而成，其具体的关系式可表示为

(6)

图2中阴影部分的面积即为塑性应变能密度。与单一载荷作用下的塑性应变能密度求解相比，复杂载荷循环作用下的塑性应变能密度还包含封闭环以外的部分塑性应变能密度值，主要体现在式(6)等号右边第二项。

总应变能密度作为衡量损伤的参数，可由塑性应变能密度和拉伸正弹性应变能密度相加得到，即

ΔWt=ΔWp+ΔWe+

(7)

2 焊缝材料参数获取

本文主要研究电动轮自卸车车架对接接头疲劳性能，因而设计一种厚度为6 mm的焊接接头，试件的设计尺寸图和实物见图3。

2.1 机械性能参数

焊接接头的单调拉伸试验设备采用MTS 810型电液伺服万能材料试验机。基于位移控制，对试件施加轴向单调拉伸载荷直至试件被拉断为止，焊接接头安装示意图见图4。由于该材料为高应变钢材，为保护引伸计不因突发状况而遭到破坏，在材料载荷发生明显下降幅度时终止试验。最后通过数据处理得到的焊接接头工程应力应变曲线和真实应力应变曲线见图5。

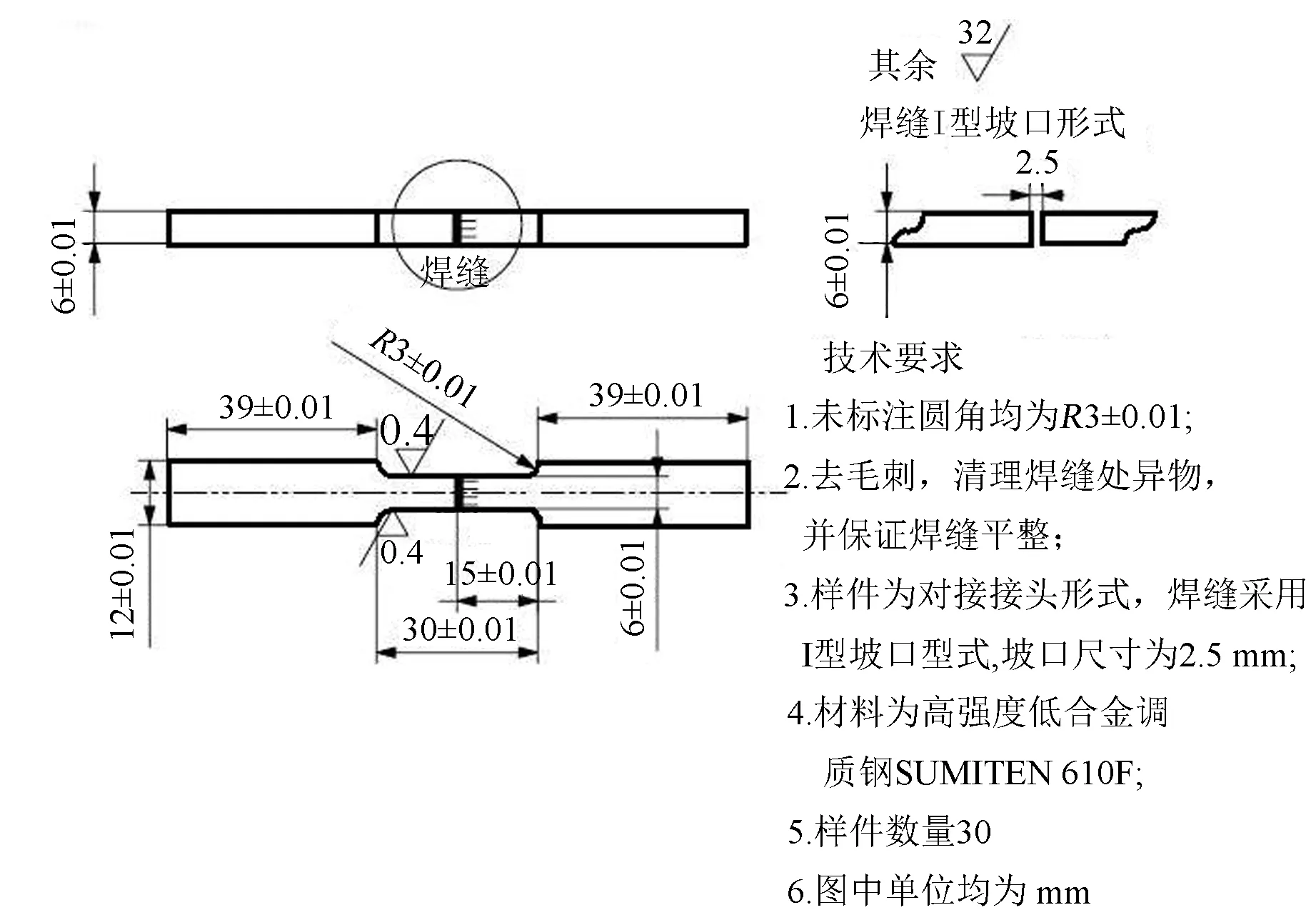
(a)焊接接头试件尺寸

(b)焊接接头试件实物图3 焊接接头试件Fig.3 Test specimen of welded joints

图4 焊接接头安装示意图Fig.4 Experimental schematic diagram of welded joints

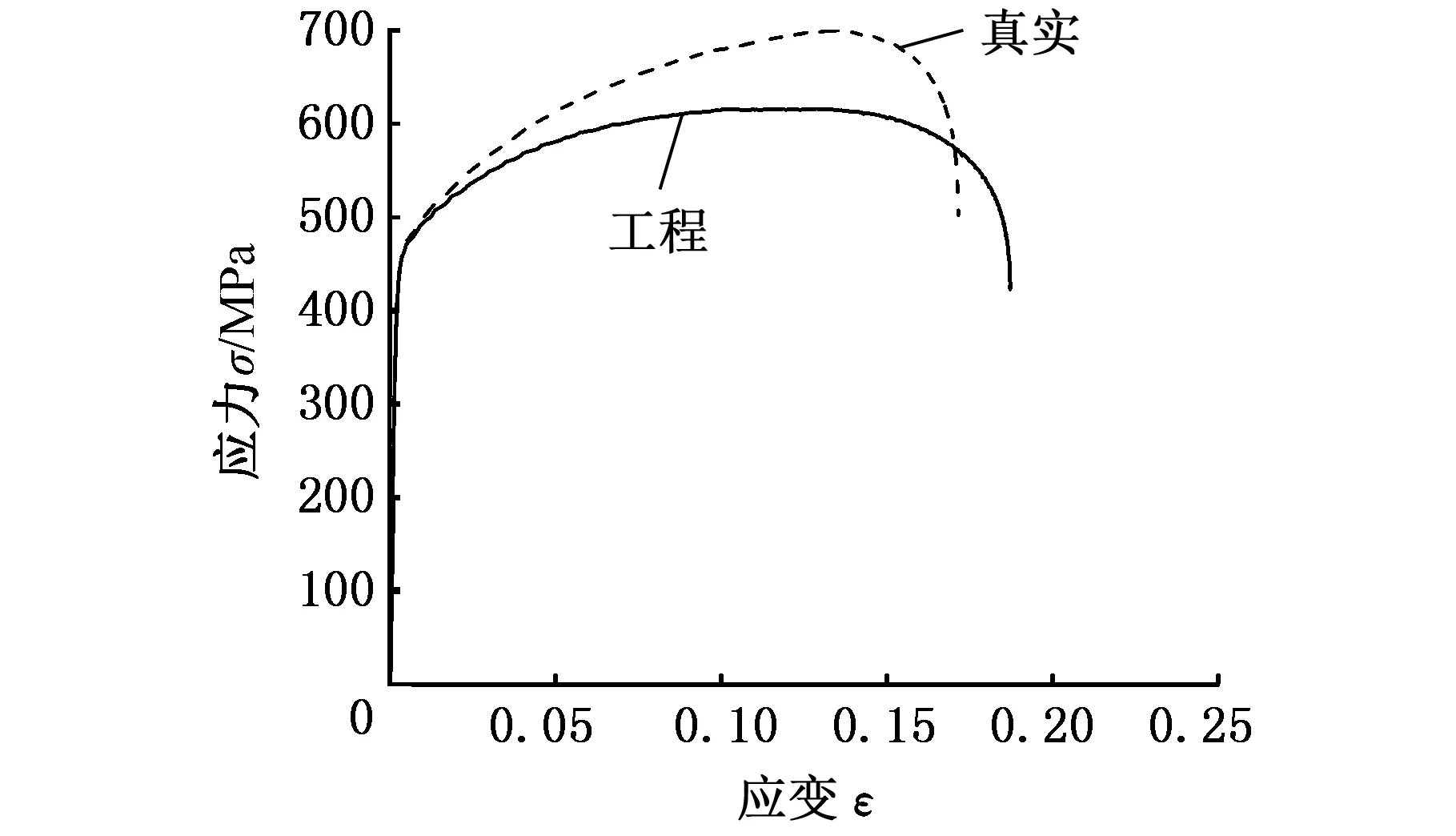
图5 焊接接头应力应变曲线Fig.5 Stress-strain curve of welded joints

焊接接头主要力学性能参数见表1。从测试结果来看，焊接接头的弹性模量参数略高于母材，这主要是焊缝区域在焊接过程材料硬化所致；其他性能参数与母材比较接近，这间接说明，该焊接接头的机械力学性能良好。

2.2 疲劳性能参数

基于应变控制的焊接接头试件疲劳寿命试验，首先需要确定不同的应变水平，通常情况下，初始应变水平可以取为略高于屈服极限所对应的应变值， 其他应变水平可以根据材料属性逐渐减小，本文研究的焊接接头应变水平分布为0.45%、0.35%、0.25%、0.15%和0.1%。

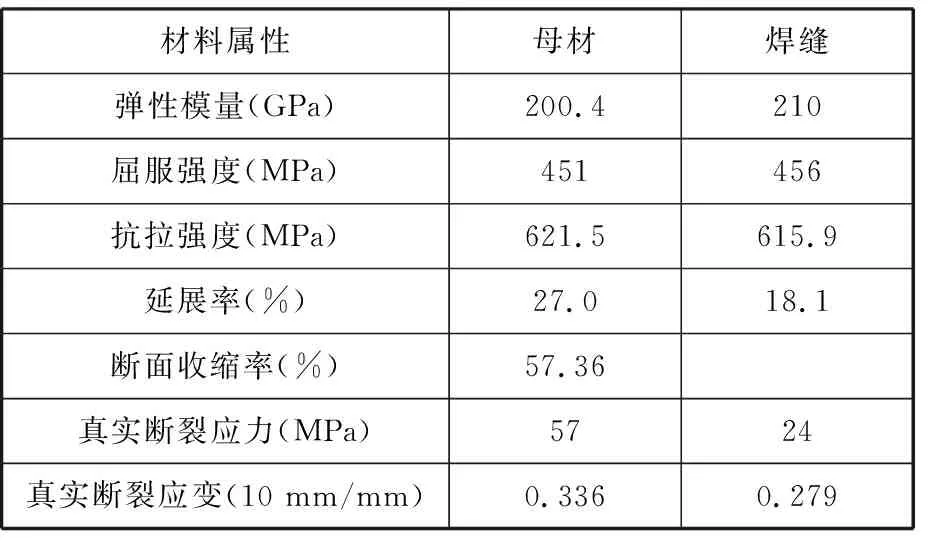
表1 焊接接头机械性能参数

根据试验结果，并结合疲劳寿命所对应的应力应变响应曲线，可以求出相应的应力幅值、应力范围、弹性应变幅值、塑性应变幅值，从而得到对数弹性应变幅值、对数塑性应变幅值与对数疲劳寿命的关系曲线，见图6，可以看出，拟合曲线和试验结果比较接近。

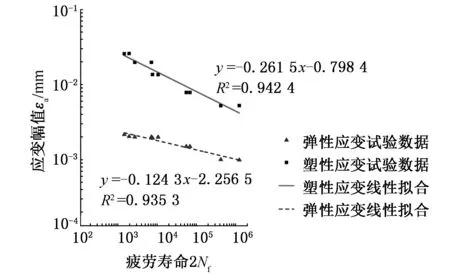
图6 弹塑性应变疲劳寿命试验结果Fig.6 Elastic and plastic strain and fatigue life test results

借助引伸计同样可以得到不同应变水平下的周期应力应变数据，其中某一试件的周期应力应变曲线见图7，可以看出，焊接接头试件在应变不变的情况下应力峰值明显减小，属于材料循环软化行为。另外， 其次周寿命的滞回曲线面积与半周寿命的滞回曲线面积相差不是太大，说明材料

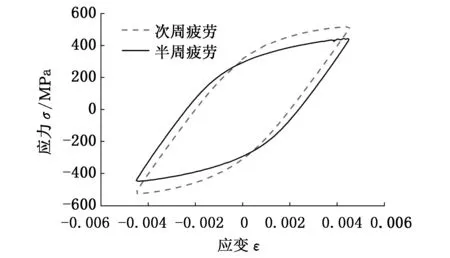
图7 某试件周期应力应变响应曲线Fig.7 Cyclic stress-strain curve for one specimen

在一定载荷作用后很快达到稳定状态。

(8)

式中，εa为应变幅值；Δσ/2为应力幅值；K′为循环强化系数。

结合车架焊缝应变疲劳寿命试验和Ramberg-Osgood方程，得到的周期应力应变响应见图8。由图8可看出，拟合的曲线与试验数据吻合良好，能够有效模拟车架焊缝的周期应力应变行为。式(8)的参数值在表2给出。

图8 周期应力应变响应Fig.8 Cyclic stress-strain response

表2 车架焊缝疲劳材料参数

要实现车架焊缝基于应变能量法的疲劳寿命预测，还需要得到材料的应变能密度和疲劳寿命的关系。结合应变能密度计算方法和周期应力应变响应曲线，即可求得不同应变水平下的总应变能密度，然后找到对应的疲劳寿命值，通过数学方程拟合得到焊缝疲劳材料特性。参考文献[11]，本文利用幂函数拟合总应变能密度和疲劳寿命的关系，其一般数学方程可表示为

(9)

式中，Nf为疲劳寿命；A为应变能密度系数；B为应变能密度指数。

结合车架应变疲劳寿命试验数据，式(9)的参数值见表2。其中，车架焊缝应变能密度疲劳寿命曲线见图9。由图9可看出，拟合曲线与试验结果相差不大，幂函数能够有效表示两者的关系。

图9 总应变能密度疲劳寿命曲线Fig.9 Total strain energy density and fatigue life curve

3 车架多载荷步非线性有限元分析

3.1 有限元模型建立及验证

考虑到车架是由各种厚度的钢板和一部分圆管组合焊接而成，具有薄板结构特性,存在膜应力状态,同时考虑模型的大型性和计算硬件的实际情况等，决定采用壳单元对车架进行离散。电动轮自卸车车架上负载质量较大的部件主要有动力总成、燃油箱、货物与车厢、左、中、右甲板、散热器以及液压油箱，其重心位置均通过其几何结构的质心求得，主要的集中质量点利用Mass单元模拟，刚性耦合连接利用Rbe3单元模拟，得到的车架有限元模型的单元总数为87 932，节点总数为82 867。最终建立的车架有限元模型见图10。

收缩裂缝主要是指混凝土因外界因素所致的体积变化，一般情况下是干缩裂缝与塑性裂缝，其中塑性收缩裂缝的发生时间主要在混凝土初凝阶段，此时具有较高的水化反应，水分会出现大量增加的情况，导致混凝土失收缩。干裂裂缝主要在混凝土硬化前后，表层混凝土水分散发比较快，内部结构热量散发相对较慢，直接导致混凝土表面收缩性相大，内部收缩性小，致使收缩情况产生一定的不均匀，从而发生收缩裂缝现象。

图10 车架有限元模型Fig.10 Finite element model of frame

车架在满载静止状态下主要承受各附加装置以及货物的重力，重力通过对建立的质量点单元施加重力加速度来实现；然后，对前后悬架下支点的自由度进行约束，释放车架前进方向的自由度以及3个转动自由度。通过MSC.Nastran数值求解计算，车架的最大主应力云图和最小主应力云图分别见图11和图12。可以看出，在车架纵梁底板与尾梁内侧板拐角处的最大应力值达120 MPa，由于该位置结构几何形状较复杂，且受到货物重力作用，因此应力水平较高。另外，车架纵梁顶板与尾梁内侧板处、前后悬架铰接位置和后牵引接头位置，最大主应力水平分别在100 MPa、60 MPa和50 MPa左右，其他位置的应力水平均较低。

图11 车架最大主应力云图Fig.11 Maximum principal stress contour of frame

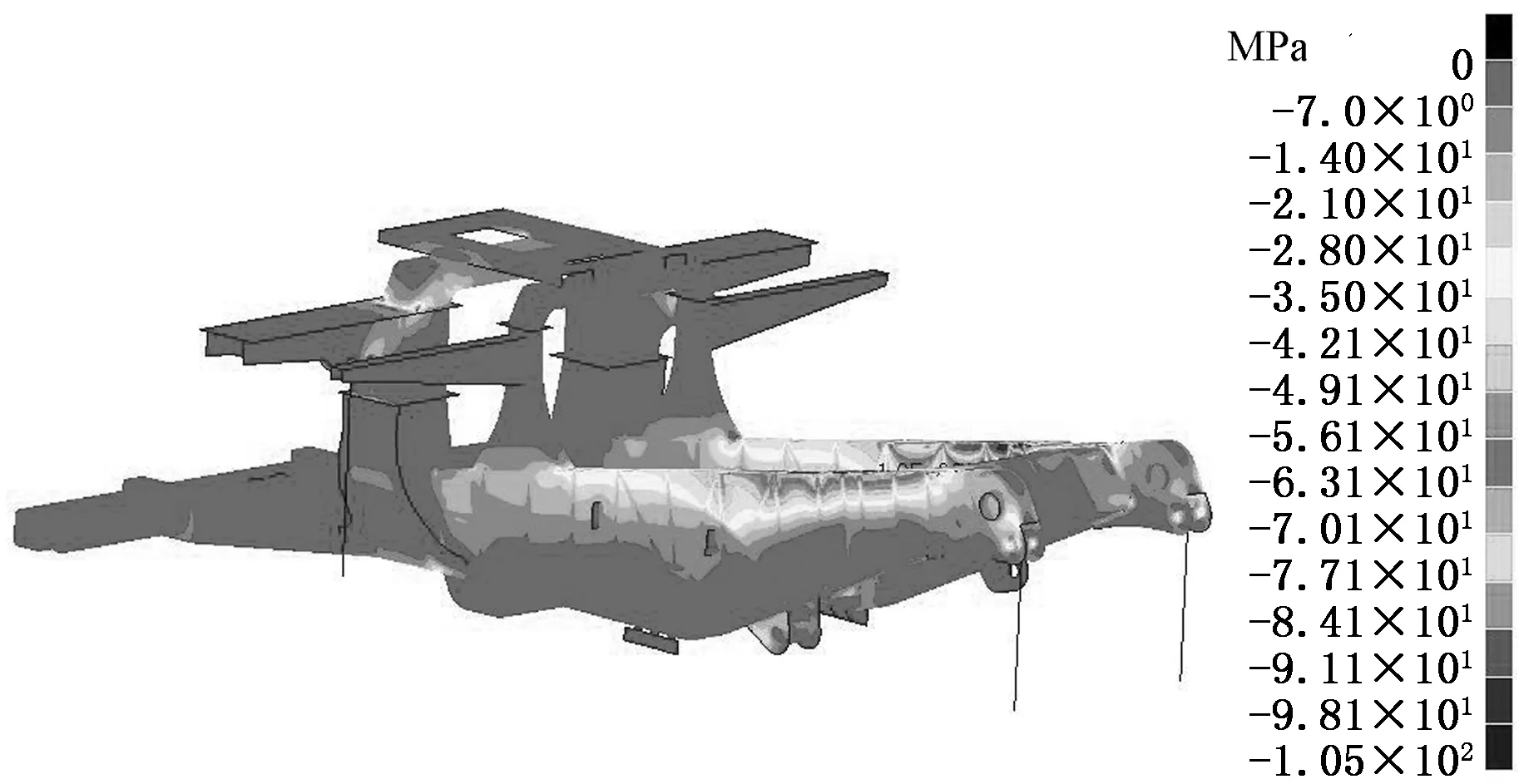
图12 车架最小主应力云图Fig.12 Minimum principal stress contour of frame

为验证电动轮自卸车车架有限元模型的准确性，对车架满载静止工况下的应力状态进行了测试。主要测试车架关键部位的应力值，从车尾往车头方向标记，左边定义为A，右边定义为B，共包括11个测点，具体位置的测点见图13，应变片具体安装位置见图14。

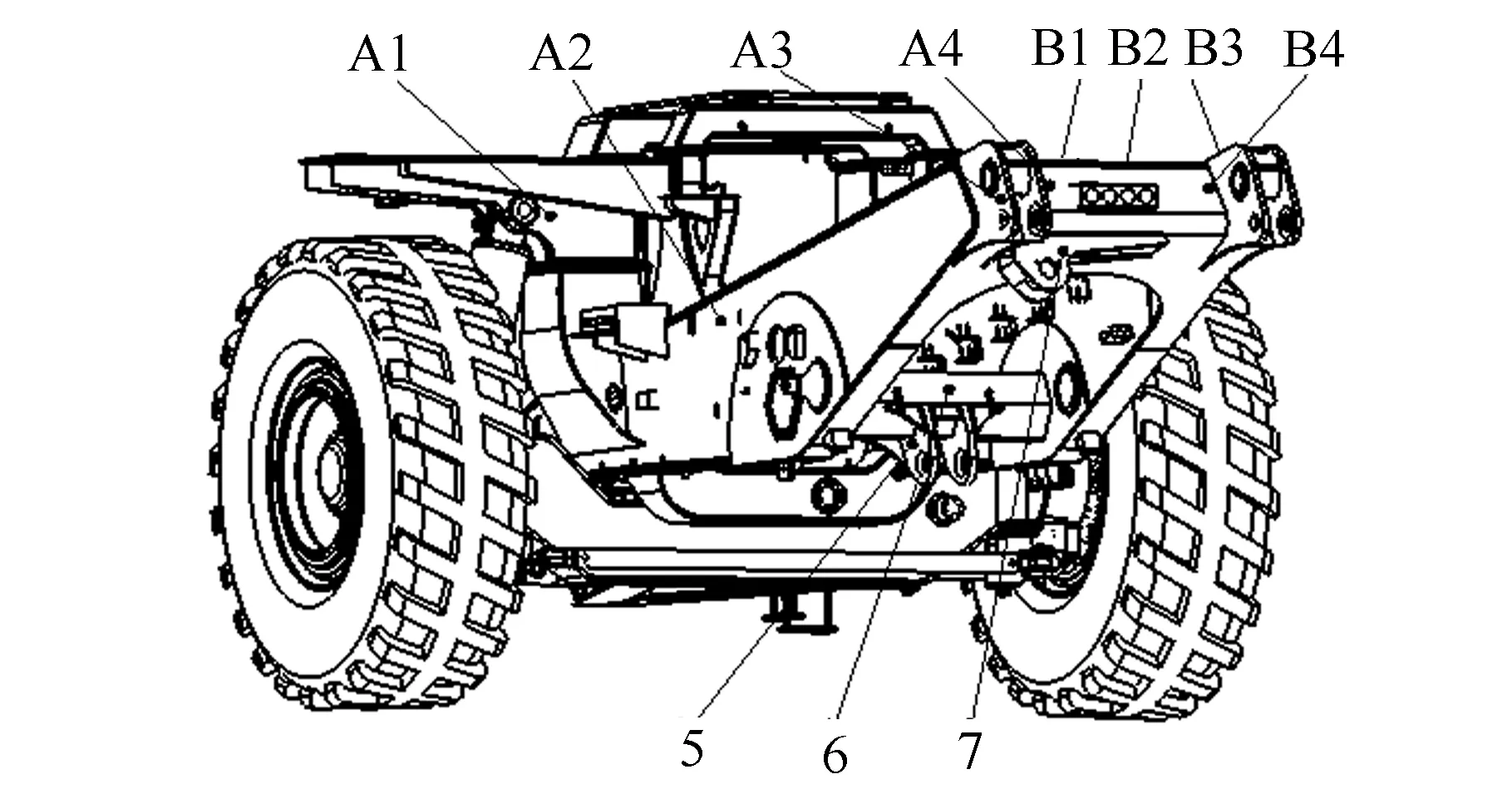
图13 车架应力测点布置图Fig.13 Measuring points layout of frame stress

图14 测点B4应变花安装示意图Fig.14 Strain rosette schematic diagram of point B4

将车架有限元分析应力结果和主要测点试验应力值进行对比，结果见表3。可以看出，测点7的误差最大，达70.5%，主要是因为满载静态有限元分析仅考虑了垂直方向的载荷，在静强度分析时没有施加后横拉杆铰接位置处的局部侧向作用力，后横向稳定杆位置处主要传递侧向载荷，实车结构可能由于货物偏载造成局部受力不均而产生一定的应力，从而使得试验结果和仿真结果误差较大。测点A3和B3误差达55%左右，其主要原因在于车架有限元模型忽略了车厢和车架之间的橡胶垫，将车厢和货物重力直接施加于车架相应节点上，并且由于车架纵梁顶板和底板与车架尾梁之间存在几何过渡，一定程度上造成该位置局部应力集中，从而出现大面积高应力区域，某种程度上造成了高应力区域的转移。除上述测点误差较大以外，其他测点的有限元分析结果和试验结果误差绝大部分在10%以内，部分有限元分析结果和试验结果非常接近，从而充分验证了本文所建立的车架有限元模型的准确性，也为后续依据该模型进行车架多载荷步非线性有限元分析奠定基础。

表3 车架仿真和试验应力结果对比

3.2 多载荷步非线性有限元分析

当车架焊缝的材料力学行为和结构载荷受力情况确定后，借助有限元分析对其进行求解计算，从而得到循环载荷作用下不同单元和节点的应力应变信息。根据试验得到的应力应变响应数据，可以求出仿真分析所需要的塑性应变和应力之间的对应关系，并将其作为车架焊缝的非线性材料参数。然后将车架焊缝有限元分析分成3个载荷步，第一个载荷步为首次加载过程，模拟车架焊缝开始受到拉伸或压缩作用；第二个载荷步为卸载过程，该过程是计算求出车架焊缝单元应力应变滞回曲线的必要步骤；第三个载荷步为再次加载过程。本文所需要的载荷来自多体动力分析[14]，分别对车架满载水平路面和下坡转弯制动路面的主要铰接点载荷时间历程进行等效处理。其中，满载水平路面车架左前悬架和前横向稳定杆主要受力方向等效载荷分别见图15和图16。

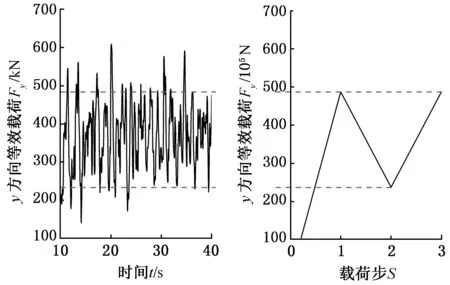
图15 左前悬架y方向等效载荷Fig.15 Direction y equivalent loading at leftfront suspension

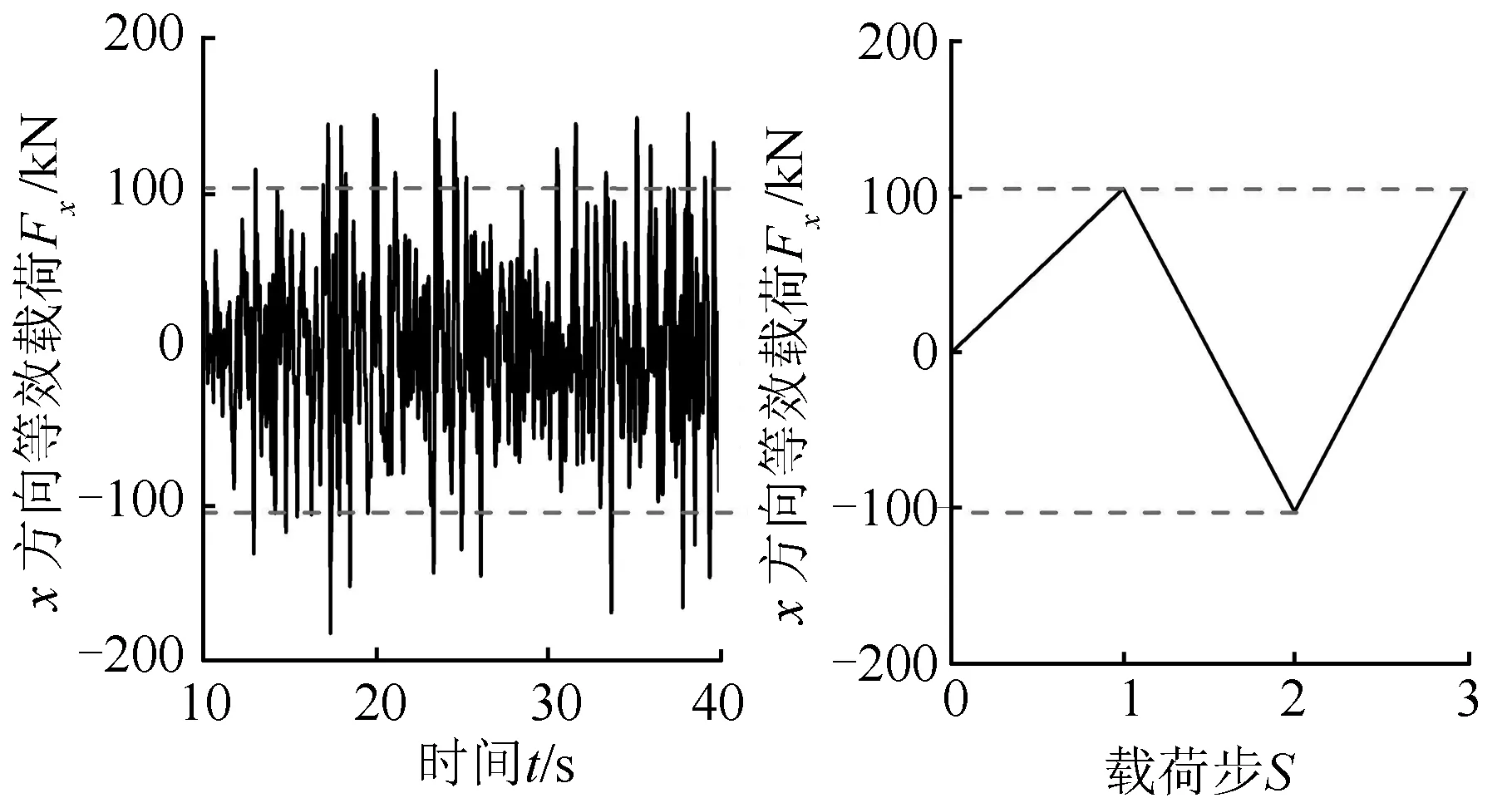
图16 前横向稳定杆x方向等效载荷Fig.16 Direction x equivalent loading at front stabilizer

车架焊缝在循环加载作用下进行的是有限元静态分析计算，其载荷呈线性关系施加于有限元模型，考虑到油气悬架非线性刚度特性对分析计算结果的影响，本文通过建立弹簧单元来模拟油气悬架，并借助inp文件来定义其刚度与位移之间的非线性特性。通过计算得到的前后悬架非线性刚度曲线见图17和图18。

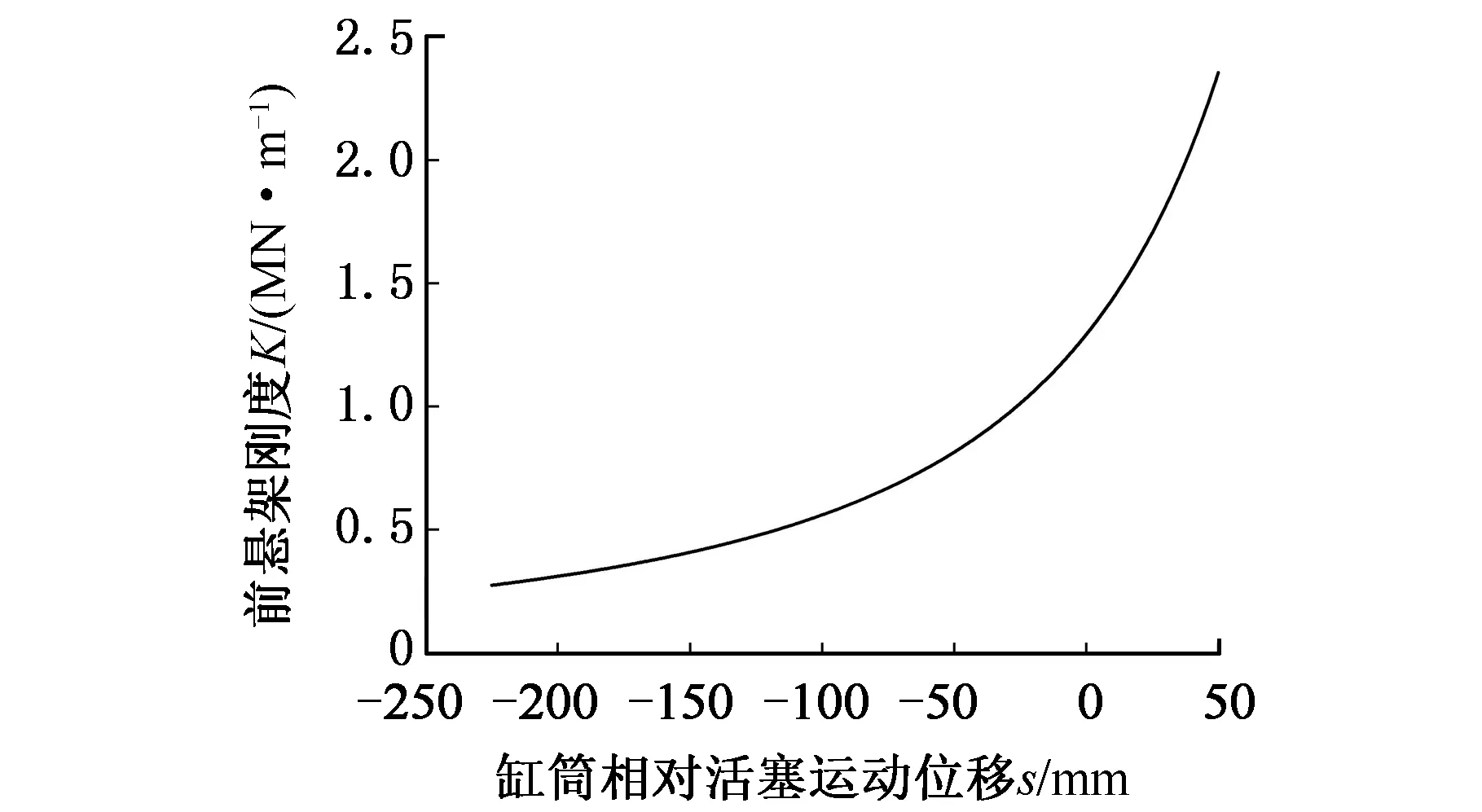
图17 前悬架刚度曲线Fig.17 Stiffness curve of front suspension

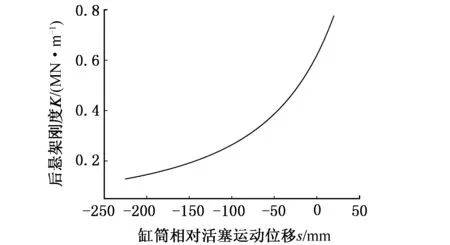
图18 后悬架刚度曲线Fig.18 Stiffness curve of rear suspension

结合试验得到的车架焊缝非线性材料行为，将其循环应力和相应的塑性应变作为材料参量，定义混合的各向同性与运动硬化法则，选择半周数据类型；将建立的弹簧单元与车架主要铰接点位置通过MPC-link方式耦合在一起，并约束弹簧下支点的自由度，将车架主要受力等效载荷施加于耦合节点上，就可以对车架焊缝有限元模型进行求解计算。本文分别对满载水平路面行驶工况和下坡转弯制动行驶工况进行多载荷步非线性有限元分析计算，第二次加载完成后利用ABAQUS求解计算得到的车架焊缝单元应力和塑性应变云图见图19～图22。

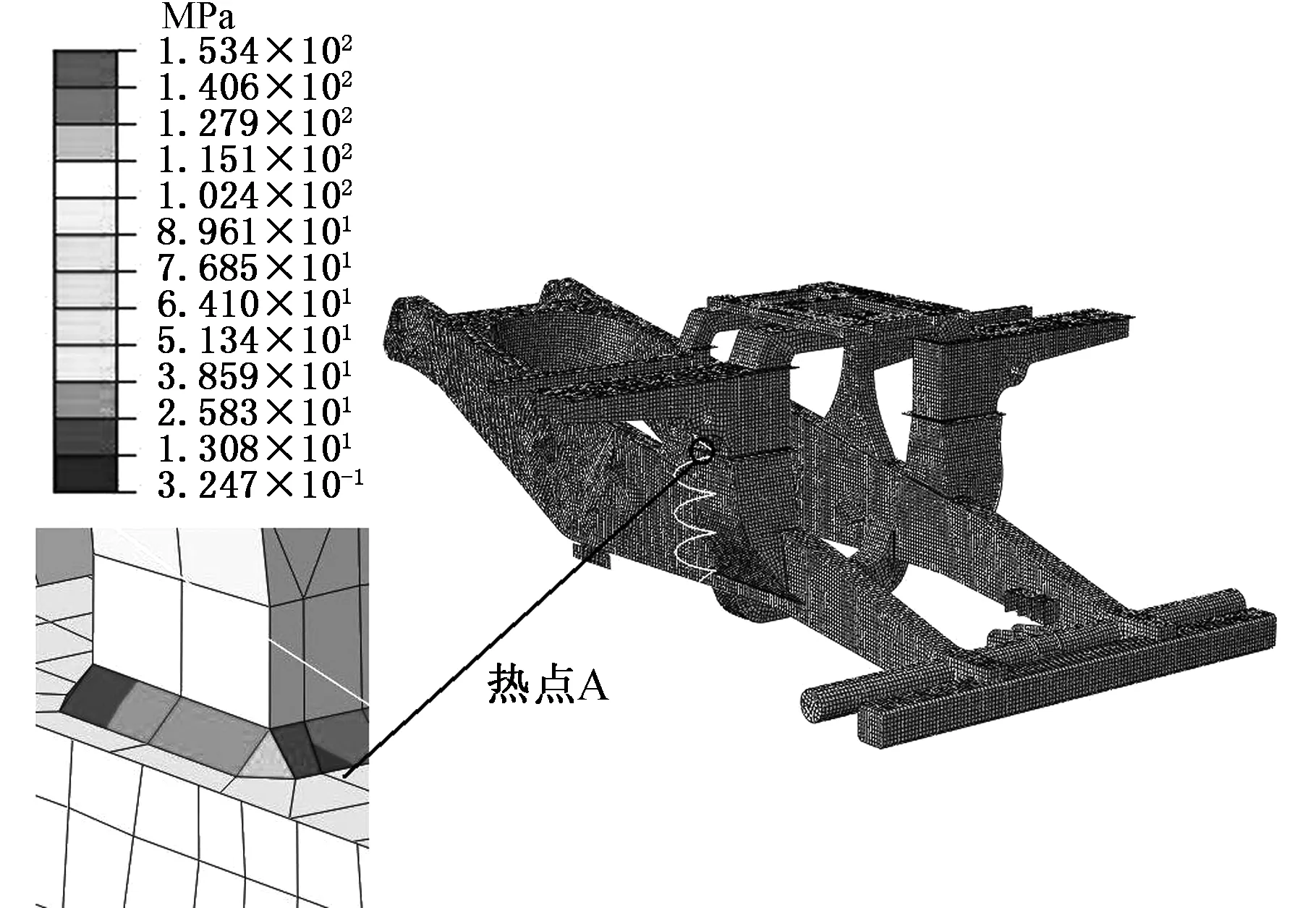
图19 满载水平路面车架焊缝应力云图Fig.19 Stress contour of frame weld seams under full loading for horizontal road surface

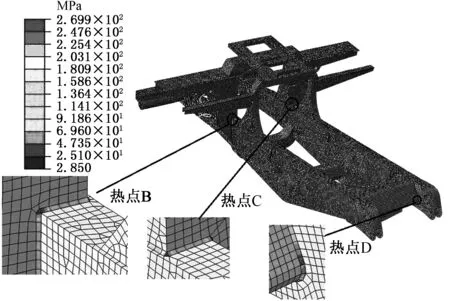
图21 下坡转弯制动路面车架焊缝应力云图Fig.21 Stress contour of frame weld seams under full loading for downhill and turning road surface

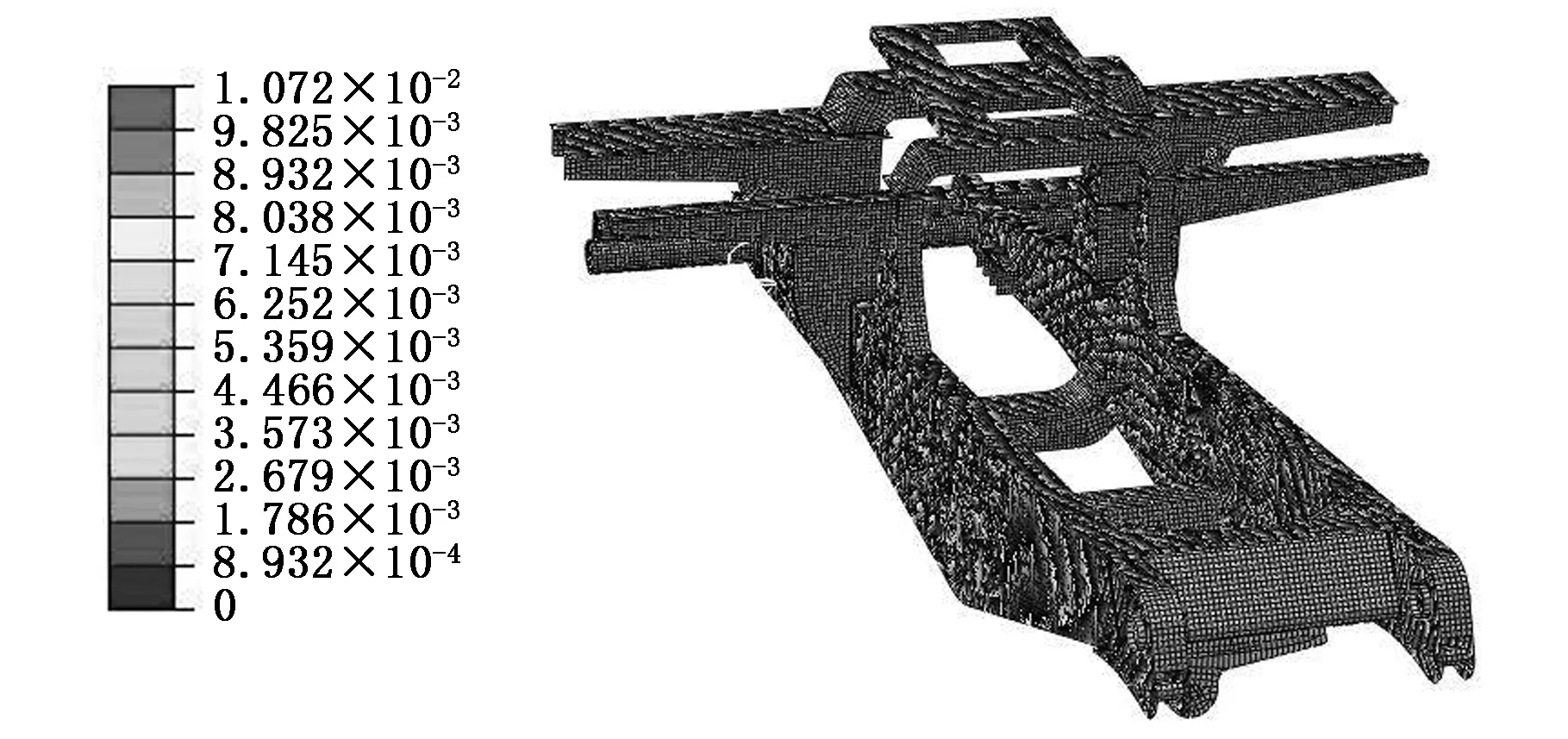
图22 下坡转弯制动路面车架焊缝等效塑性应变云图Fig.22 Equivalent plastic strain contour of frame weld seams under full loading for downhill and turning road surface

由图19可以看出，在满载水平路面行驶工况下，最大等效应力为153 MPa，出现在车架右侧龙门梁与右悬架筋板连接处，在该位置存在一定的几何过渡，且焊缝结构形式较复杂，也是主要承载部位，因此出现较大的应力值。

由图21可以看出，在下坡转弯制动路面行驶工况下，最大等效应力为270 MPa(热点D)，出现在车架右后悬架与尾梁筋板连接处，在该位置也存在一定的几何过渡，且后悬架位置载荷较大，还受到后横向稳定杆位置处的横向载荷，属于复杂交变载荷，因此出现较大的应力值。另外，在车架左右大梁位置与车架纵梁连接位置也出现了较大应力(热点B和C)，应力值也达到260 MPa左右，因此这3处位置均为疲劳寿命分析计算关注的重要位置。

4 车架多载荷步非线性有限元分析

4.1 预测结果

对于满载水平路面行驶工况，由静态分析可知，其塑性应变非常小，主要成分为弹性应变能密度，只需要求出循环载荷作用下最大等效应力，再根据式(5) 即可求出相应的应变能密度。对于车架下坡转弯制动路面行驶工况，存在一定的塑性变形，因此需要得到其循环载荷作用下的应力应变响应。不过，需要指出的是，车架主要承受垂直方向的载荷作用，因此，其应力应变量主要集中在主应力S11和主塑性应变P11上，如图23a所示(热点D)，而其他方向的应力应变值非常小，在此忽略不计；另外，车架焊缝单元除了承受拉压载荷外，还承受其他方向的作用力，因此焊缝危险单元还具有剪切应力和剪切塑性应变，如图23b所示(热点D)。根据式(5)和式(6)，即可求出不同危险节点的弹性应变能密度和塑性应变能密度，从而结合应变能密度疲劳寿命曲线实现车架焊缝疲劳寿命预测，结果见表4。依据同样的方法，可求得热点B和C的弹性应变能密度和塑性应变能密度，从而根据总应变能密度确定其相应疲劳寿命值。由于热点B和C与热点D的应力应变曲线比较相似，本文不一一给出。

(a)主应力应变响应

(b)剪切应力应变响应图23 车架焊缝热点D应力应变曲线Fig.23 Stress-strain curve of frame weld seam at point D

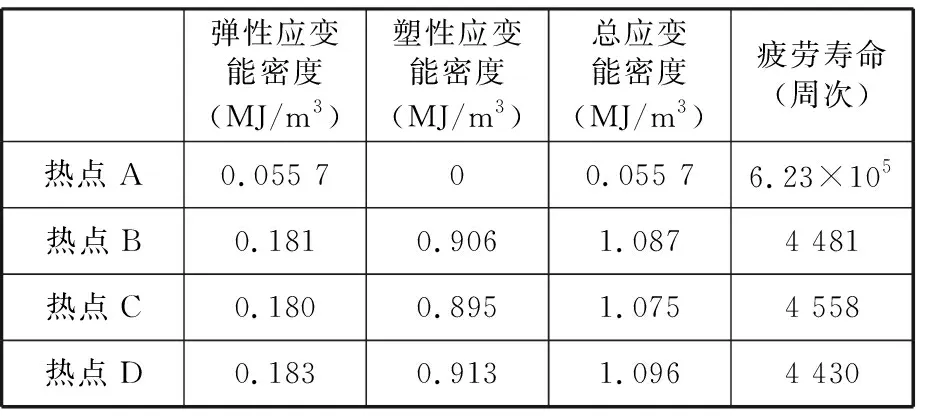
表4 应变能量法车架焊缝疲劳寿命预测结果

4.2 对比分析

为说明本文提出的改进应变能量法的有效性，将其疲劳寿命计算结果以及传统应变能量法(不考虑封闭环以外的应变能密度)疲劳寿命计算结果与构件实际失效位置进行对比，见图24和图25，从裂纹的起始路径和痕迹信息来看，属于疲劳失效。而疲劳寿命预测的危险区域与实车焊缝开裂的位置非常接近，热点B和热点C对应于车架焊缝开裂位置1和2，这说明，基于应变能量法的车架焊缝疲劳寿命预测结果可靠。另外，在发现车架焊缝开裂位置1和2一个月之后，实车在预测的热点D位置也发现了微小裂纹，由于矿山考查条件有限，未能给出开裂实物图。在实际工作中，热点D位置附近车架纵梁位置有橡胶垫缓冲装置，而数值模拟计算中没有考虑该因素，因此导致该位置疲劳寿命计算结果与实际失效时间存在误差。

图24 车架裂纹位置1(热点B位置)Fig.24 Crack 1 in left frame beam (close to point B)

图25 车架裂纹位置2(热点C位置)Fig.25 Crack 2 in right frame beam (close to point C)

结合矿山实际工况考察，电动轮自卸车每天经过该下坡转弯制动路面行驶工况的次数为10左右，同时考虑满载水平路面工况造成的损伤(主要是弹性应变能密度对应的疲劳损伤)，根据改进应变能密度法预测得到的车架焊缝主要热点B、C、D点疲劳寿命大约为13个月左右；而根据传统应变能密度法计算得到的总应变能密度约为0.911 MJ/m3，对应的疲劳寿命大约为6 012周次，考虑满载水平路面工况造成的损伤，计算疲劳寿命相当于15个月左右。而车架焊缝实际开裂时间为8个月左右，显然，基于改进应变能密度法的预测结果与车架焊缝实际开裂时间更加接近，进一步说明了该方法的有效性。基于改进应变能密度法的预测结果比车架焊缝实际开裂时间要保守，这可能是因为电动轮自卸车实际运行路面要比多体动力学仿真分析计算的路面工况更加恶劣，以至于恶劣工况下车架承受的实际载荷更大。

5 结论

(1)本文针对复杂载荷作用下焊接结构应力应变响应出现非完全封闭而交叉的现象，提出了一种改进的应变能密度计算方法，为电动轮自卸车车架焊缝疲劳寿命预测提供理论参考。

(2)通过设计焊接接头试验试件进而开展试验研究，得到焊缝的机械性能和疲劳性能参数，并构建应变能密度疲劳损伤模型，从而为车架多载荷步非线性有限元模拟所需要的材料参数提供可靠而有效的数据基础。

(3)建立电动轮自卸车车架有限元模型，在其有效性得到验证的基础上，等效车架随机载荷谱，考虑油气悬架非线性刚度特性，开展多载荷步非线性有限元分析，获得满载水平路面和下坡转弯制动路面两种工况下的应力应变响应曲线。进而依据改进的应变能密度法计算疲劳损伤参量，并将预测结果与实际开裂位置和失效时间进行对比，发现两者之间吻合较好，证明了本文方法的有效性。这为开展复杂载荷作用下电动轮自卸车车架焊接结构疲劳寿命预测研究提供了可行的新途径。