面向高效节能的复杂曲面分区数控铣削加工优化方法

赵俊花 李 丽 李玲玲 李聪波

1.西南大学工程技术学院，重庆，4007152.重庆大学机械传动国家重点实验室，重庆，400030

0 引言

复杂曲面类零部件被广泛应用于航空航天、汽车、船舶、能源、国防等领域，如航空发动机叶轮、大型舰船螺旋桨、汽轮机转子、汽车覆盖件精密模具等，其制造技术水平对国民经济发展和国防现代化建设都具有十分重要的意义[1]。三轴或五轴数控加工是当前复杂曲面类零部件较常采用的加工方法，通过精确控制数控机床上刀具和工件的相对切削运动，保证曲面加工质量、加工效率等经济性指标达到要求。然而，由于复杂曲面曲率的频繁变化特性和数控机床的复杂运动特性，导致复杂曲面数控加工存在能量消耗大、能耗特性复杂多变、能效低等问题，具有很大的节能优化空间[2]。

近年来，国内外学者围绕复杂曲面数控加工能效优化问题已开展了一些研究。RYUTA等[3]分析了五轴数控机床进给系统的运动特性并建立了进给系统的能耗模型，揭示了工件装夹定位点对进给系统能耗的影响关系。UCHIYAMA等[4]通过试验设计研究了五轴数控机床主轴系统运动与能耗的关联关系，并通过同步控制五轴数控机床的三个平移轴和两个旋转轴实现节能13.2%。XU等[5]分析了五轴机床运动特性并建立了五轴加工能耗模型，在此基础上以能耗最小为目标提出了一种复杂曲面五轴加工刀具路径生成方法，通过与几种常用刀具路径生成方法(如等残留高度法)进行比较，实现节能25%。李丽等[6]以加工时间最短和能耗最小为目标，提出了基于自适应模拟退火算法的五轴加工刀具路径生成方法，通过求解最优的刀触点间距和加工行距、刀触点连接顺序和方式，以确定能耗和加工时间综合最优的刀具路径。

目前，复杂曲面分区加工的研究较多着眼于加工时间、加工质量等经济性指标，未考虑复杂曲面分区加工对能耗的影响关系。从复杂曲面分区出发，研究复杂曲面五轴加工高效、节能优化方法，对降低复杂曲面加工能耗、提高加工效率具有重要意义。鉴于此，本文以复杂曲面五轴铣削为研究对象，提出一种面向高效节能的复杂曲面分区五轴铣削优化方法。

1 问题描述

本文的复杂曲面分区铣削优化问题描述为：复杂曲面的几何特征直接影响加工机床、加工刀具、切削参数与刀具路径的选择，由此影响加工工件的表面质量、加工效率和能量消耗等。根据复杂曲面曲率特性，运用模糊C均值聚类(FCM)算法对复杂曲面进行分区；在此基础上，针对每一个分区曲面，选取机床允许范围内的铣削参数(主轴转速和进给率)与几种常用刀具路径，采用正交试验设计开展复杂曲面分区铣削加工试验，获取能耗和加工时间最优的切削参数和刀具路径；最后，对复杂曲面分区铣削优化结果分别开展仿真和加工试验验证，并将曲面分区铣削优化结果与传统曲面整体铣削结果进行对比验证。复杂曲面聚类分区铣削优化方法见图1。

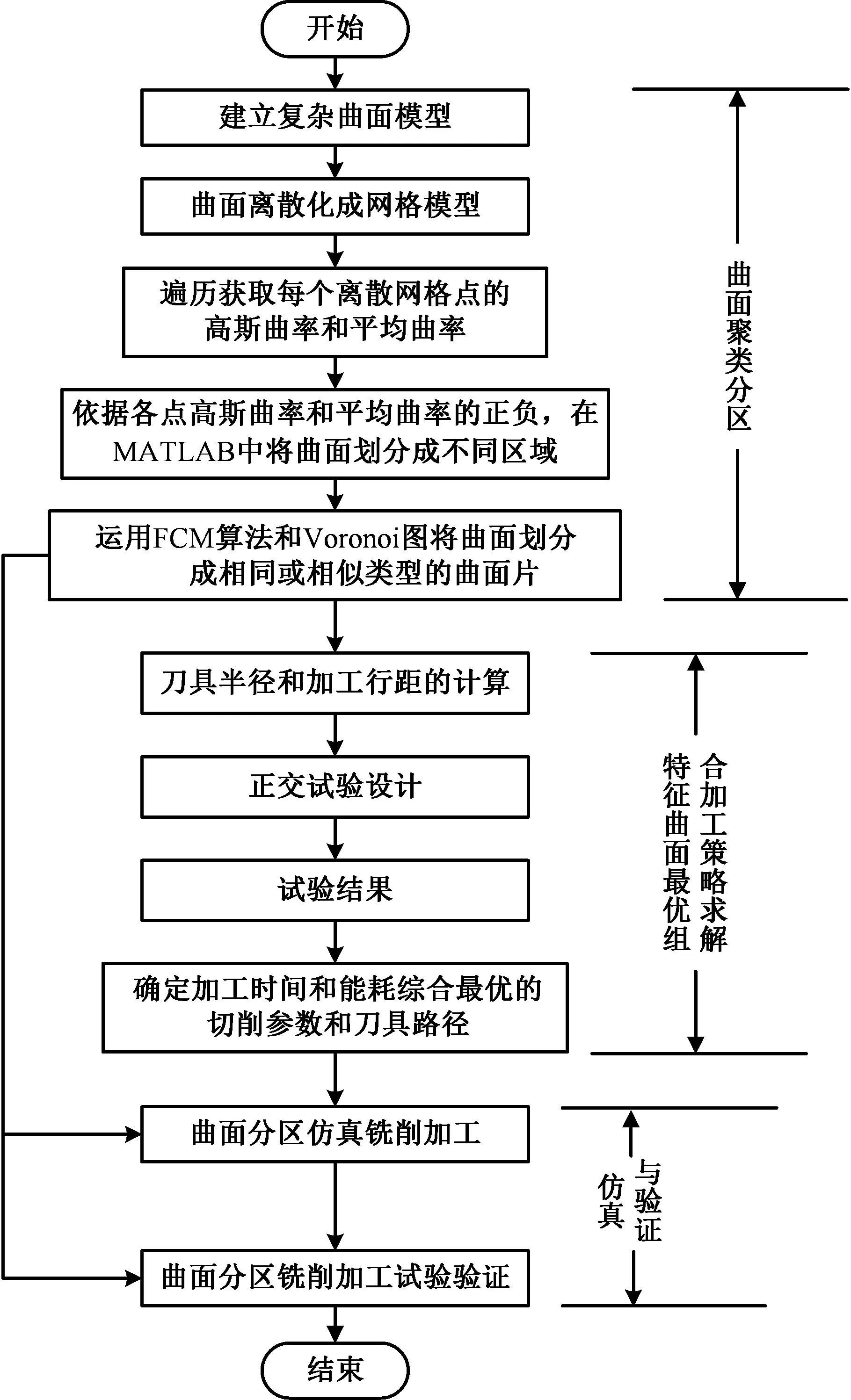
图1 复杂曲面聚类分区优化铣削方法Fig.1 Complex surface clustering partition optimization milling method

本文复杂曲面分区铣削优化问题的相关假设条件如下：①复杂曲面分区优化铣削加工是在加工工件、数控机床、球头铣刀已经确定的前提下开展的；②在球头铣刀加工曲面过程中，在等残留高度h一定的条件下，考虑到曲面曲率特征的不断变化，导致切削深度和切削宽度改变，本文仅选择主轴转速和进给率作为优化的铣削参数；③仅对加工工件在单工步、不换刀情况下进行曲面分区铣削优化研究。

2 复杂曲面聚类分区

首先，根据复杂曲面的曲率特性作几何特征分类；然后在此基础上，对复杂曲面进行离散化处理并初步划分形成不同区域；最后，基于FCM算法分片，产生相同或相似的曲面片族。

2.1 复杂曲面几何特征分类

本文采用NURBS曲面描述复杂曲面。首先根据NURBS曲面曲率特性对曲面进行分类。平均曲率的正负代表了曲面凹凸性，高斯曲率的正负代表了曲面的弯曲程度。kH为曲面的平均曲率，kG为曲面的高斯曲率，计算公式[2]如下：

(1)

(2)

式中，E、F、G为NURBS曲面S(u,v)的第Ⅰ类基本量；L、M、N为NURBS曲面S(u,v)的第Ⅱ类基本量。

由曲面上某点处的平均曲率和高斯曲率的符号可以判断该点的类型和该点所处区域的形状[12]，具体见表1。其中，高斯曲率为正、平均曲率为零这样的点不存在，未在表中列出。

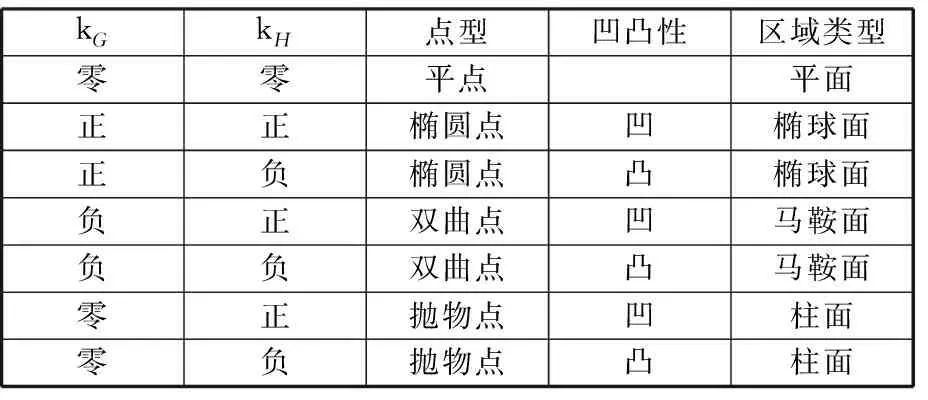
表1 点的类型和曲面区域类型

2.2 曲面离散化与初步划分

为得到曲面的点云信息，首先对曲面进行离散化。曲面离散的基本过程是在曲面的u向、v向各选一条等参数线,如s(u,0)、s(0,v)，按曲面大小离散这两条等参数线，记录这些网格点的坐标值，形成曲面参数域的离散点。

在此基础上，对复杂曲面进行初步划分。具体过程为：首先建立NURBS复杂曲面(图2)，将该曲面离散成40×40的网格模型(图3)，并在离散化网格模型的基础上，遍历获取分布在网格上每一个离散点的高斯曲率和平均曲率；运用MATLAB语言编程，依据表1判断每个点的类型，同一类型的点集被聚集在一个面域，相邻的两个点的面型发生变化时，该点就成为边界点，不同的面域之间被明显地分隔，将所有的边界点连起来就形成了曲面的划分边界。在MATLAB中进行曲面初步划分，得到的二维图和三维图分别见图4和图5。

图2 复杂曲面Fig.2 Complex surface

图3 曲面离散网格模型Fig.3 Surface discrete grid model

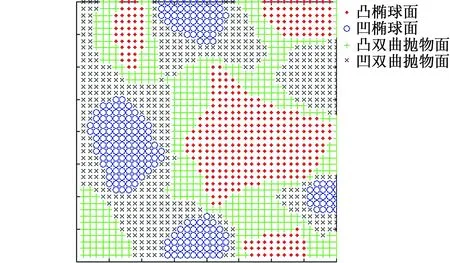
图4 曲面初步划分二维图Fig.4 Preliminary partition of surface in 2D

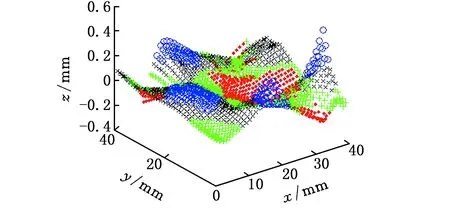
图5 曲面初步划分三维图Fig.5 Preliminary partition of surface in 3D

2.3 基于FCM算法的曲面分片

FCM算法相比于传统的模糊聚类算法，具有计算简单、运算速度快、抗噪性强、在计算机上易于实现等特点[13]。在曲面初步划分后，利用FCM算法迭代过程，找到每个曲面区域的聚类中心(如图6中“*”所示)。在此基础上，为了得到明显的曲面边界，引入 Voronoi 图将各边界点连接起来。图 7为Voronoi生成的曲面边界。为方便后续曲面分片，对每个曲面区域的聚类中心和边界顶点编号，再将二维图上划分的曲面区域的每个边界点，按照其在网格上的位置分布通过坐标映射投影到曲面上进行曲面分割，从而得到坐标映射和曲面分片,分别见图8和图9。曲面分片后，可将邻近相同类型的曲面片合并，以减少分片数量，方便后续曲面分区加工。

图6 曲面区域聚类中心Fig.6 Cluster center of surface area

图7 曲面区域边界Fig.7 Boundary of surface area

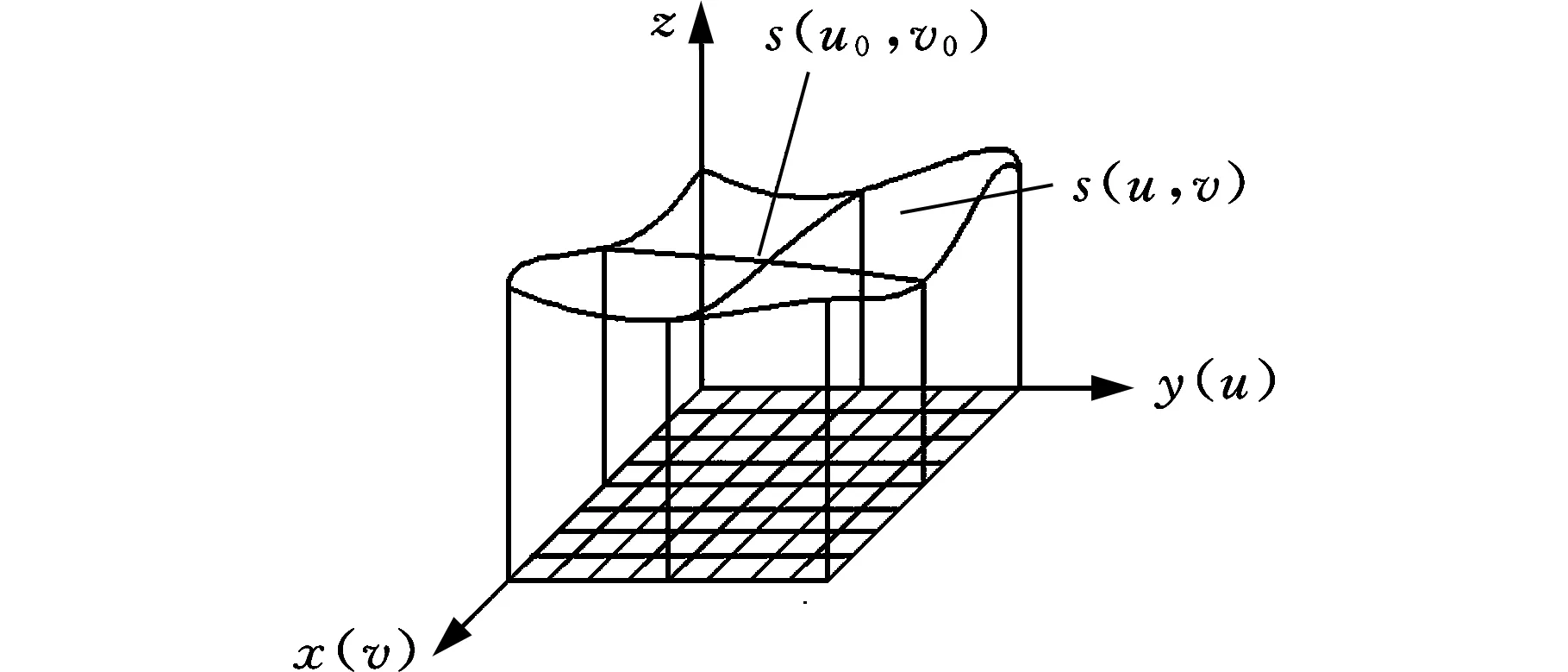
图8 坐标映射Fig.8 Coordinate mapping

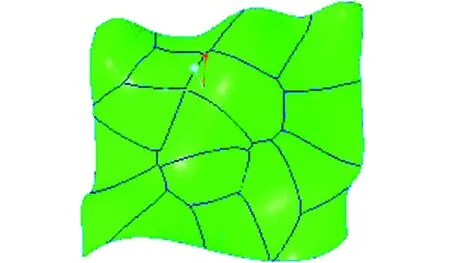
图9 曲面分片Fig.9 Surface slicing

3 复杂曲面聚类分区高效节能铣削正交试验

选用直径d=30 mm 的C6061铝合金棒作为正交试验的加工工件。该工件的曲面模型和曲面二维划分分别见图10和图11，曲面分片图见图12。图12中，深灰区域为椭球面(图13a)，浅灰区域为马鞍面(图13b)。本节针对椭球面和马鞍面这两种曲面，分别设计复杂曲面分区铣削优化正交试验(L934)。

图10 曲面模型Fig.10 Surface model

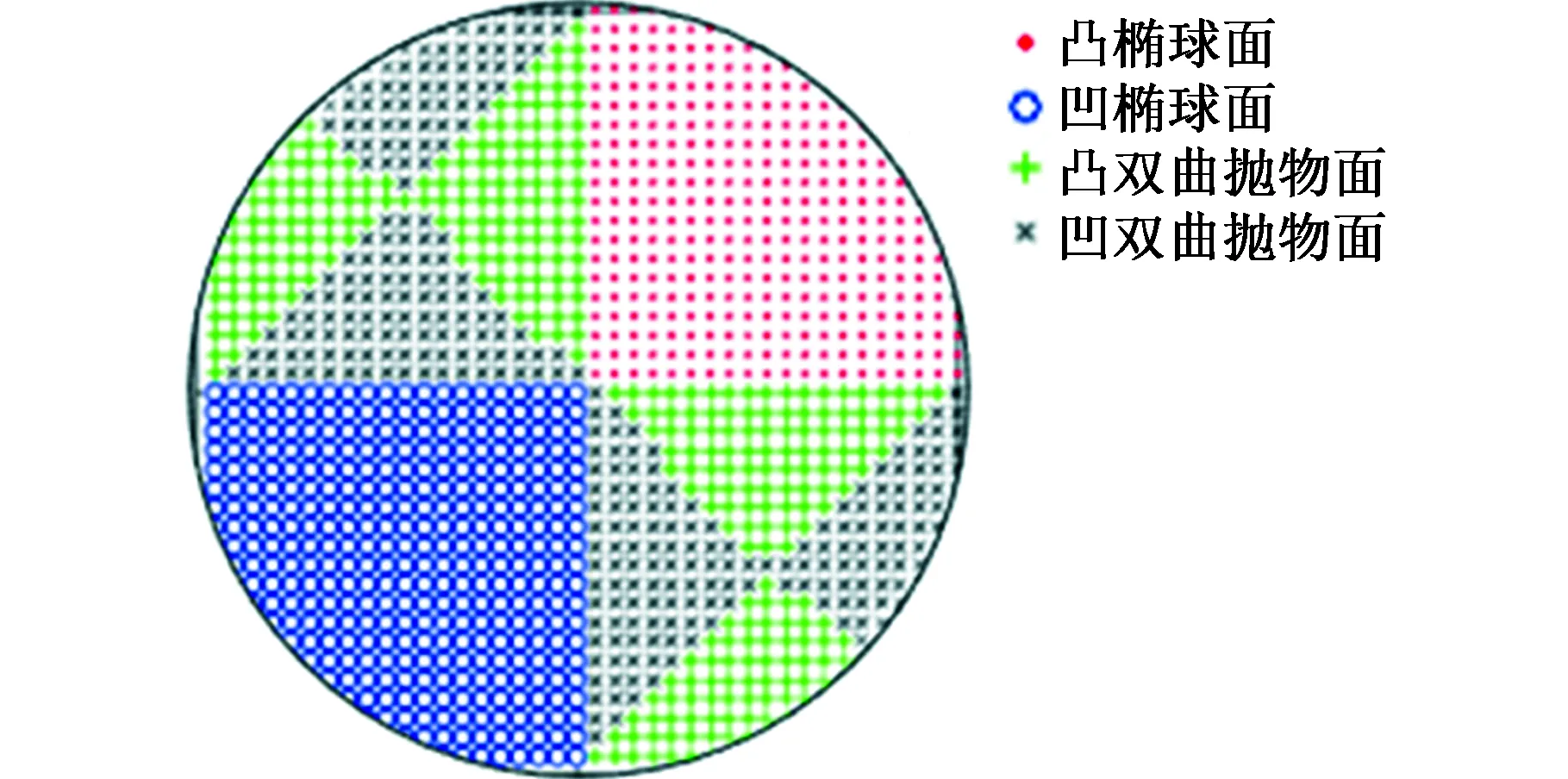
图11 曲面二维划分Fig.11 Partition of surface in 2D

图12 加工工件曲面分片Fig.12 Surface slicing of machining workpiece

(a)椭球面 (b)马鞍面图13 试验曲面模型Fig.13 Surface model in the test

3.1 试验条件

(1)加工机床。采用济南三机床有限公司的JTVC650B立式加工中心，用日置PW6001功率分析仪来监测机床切削过程的实时功率。

(2)加工刀具。在进行曲面加工时，为避免发生干涉，球头铣刀刀具半径r应小于待加工表面凹处的最小曲率半径[6]，即r<1/kmax,kmax为加工曲面凹处的最大法曲率，且kmax>0。本文采用2刃的钨钢球头铣刀，粗加工刀具直径D1=6 mm，半精加工刀具直径D2=3 mm。

(3)切削条件。采用干切削完成复杂曲面的铣削过程。粗加工留余量0.5 mm，半精加工深度ap为0.5 mm,残留高度h为0.06 mm。

(4)加工行距的确定。为了保证加工精度及刀具路径的合理性，本文通过等残留高度法[2]得到刀具路径行距L，其计算公式[14]如下：

(3)

式中，R为曲率半径；h为残留高度，曲面曲率为凹时符号取“-”，曲率为凸时符号取“+”。

3.2 试验方案

(1)因子水平设计。本文正交试验的设计变量主要包括主轴转速、进给率、刀具路径。其中，切削参数应根据刀具、工件及机床刚性范围来确定；刀具路径选择平行铣削、45°平行铣削、流线铣削这3种方式。正交试验的因子水平见表2。

表2 因子水平表

(2)能耗和加工时间综合评价指标。本文中复杂曲面分区铣削优化的目的是：在等残留高度条件下，以能耗和加工时间为综合目标进行复杂曲面分区优化铣削加工。目标函数为

F(L)=w1E(n,vf,ψ)+w2T(n,vf,ψ)

式中，E为加工能耗；T为加工时间；ψ为刀具路径生成方式；vf为进给率；n为主轴转速；w1、w2分别为机床能耗与加工时间的影响权重，w1=w2=0.5。

3.3 试验结果分析

分别针对表2中的因子水平表，开展复杂曲面分区铣削加工试验，测量得到总能耗和加工时间数据，见表3。

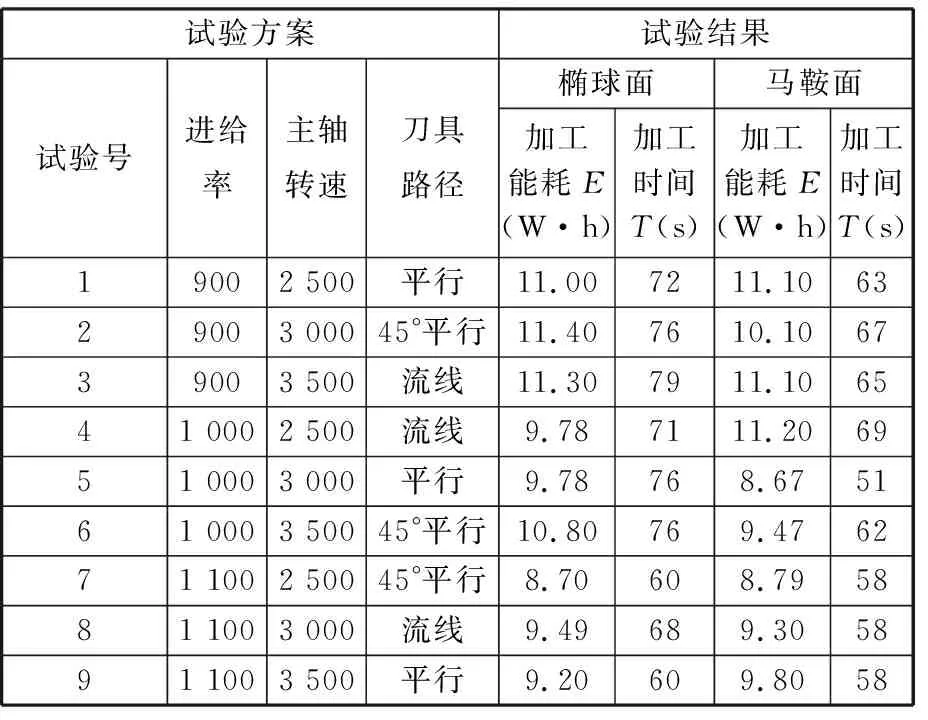
表3 曲面铣削参数与刀路方式最优匹配数学试验

(1)能耗情况分析。从表3中可以看出：对于椭球面加工，不同的切削参数与刀具路径方案产生的能耗有明显差异，其中，最低能耗是8.70 W·h,最高能耗是11.40 W·h，通过方差分析可以发现进给率对其加工能耗的影响显著，刀具路径对能耗有一定影响；对于马鞍面加工，最低能耗是8.67 W·h,最高能耗是11.20 W·h，进给率对能耗的影响程度最大。

(2)加工时间分析。从表3中可以看出：对于椭球面加工，其最短加工时间是60 s,最长加工时间是79 s，进给率和刀具路径对加工时间的影响最为显著，对主轴转速的影响次之；对于马鞍面，其最短加工时间是58 s,最长加工时间是69 s，进给率对加工时间的影响程度最大。

(3)能耗与加工时间综合分析。综合考虑加工能耗和加工时间，椭球面加工的最优组合选取进给率1 100 mm/min、主轴转速2 500 r/min的平行铣削方式；马鞍面加工的最优组合选取进给率1 100 mm/min、主轴转速3 000 r/min的45°平行铣削方式。

4 案例应用验证

本节对椭球面和马鞍面的最优切削参数与刀具路径方案，开展仿真与试验加工验证，同时，将复杂曲面分区铣削加工结果与传统曲面整体铣削结果进行对比，以验证所提方法的有效性。

4.1 曲面分区仿真铣削加工

采用第3节中椭球面和马鞍面的最优组合切削参数和刀具路径，对C6061铝合金棒工件进行曲面分区铣削加工前的仿真，并与曲面整体铣削加工仿真作对比，本文研究主要集中在半精加工阶段。在MasterCAM中用圆柱体毛坯进行仿真铣削加工，曲面分区铣削时，椭球面采用进给率1 100 mm/min和主轴转速2 500 r/min的平行铣削方式，马鞍面采用进给率1 100 mm/min和主轴转速3 000 r/min的45°平行铣削方式；曲面整体铣削时，在进给率1 100 mm/min和主轴转速3 000 r/min的条件下分别进行平行铣削、45°平行铣削和流线铣削这3种单一刀轨铣削。根据铣削结果，比较分区铣削和3种单一刀轨铣削的刀具路径长度和切削时间，结果见表4。曲面的3种单一刀轨铣削和分区铣削的仿真刀具路径见图14。

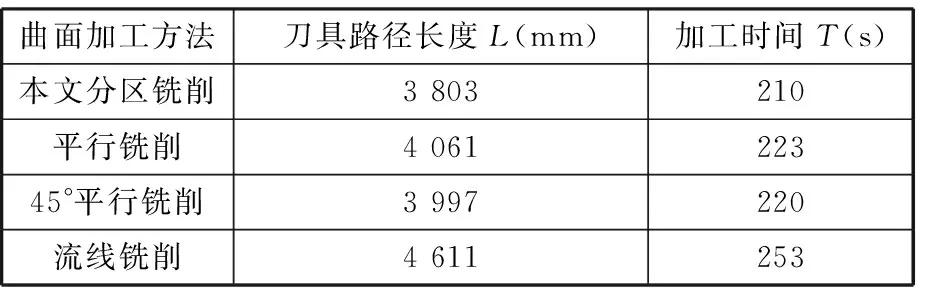
表4 仿真结果

(a)曲面平行铣削(b)曲面 45°平行铣削

(c)曲面流线铣削(d)曲面分区铣削图14 曲面分区铣削与单一刀轨铣削的刀具路径比较Fig.14 Comparison of the generation toolpaths between milling patch by patch and milling globally

根据表4的仿真结果可知，本文曲面分区铣削加工方法生成的刀具路径长度较3种单一刀轨铣削加工方法生成的刀具路径长度显著减短，加工时间也明显缩短。其中，分区铣削的刀具路径长度较平行铣削减短了6.4%，较45°平行铣削减短了4.9%，较流线铣削减短了17.5%；分区铣削的加工时间较平行铣削缩短了5.8%，较45°平行铣削缩短了4.5%，较流线铣削缩短了17.0%。由此可知，曲面分区铣削加工方法较单一刀轨的流线铣削加工方法在刀具路径长度和加工时间上的优势突出。

4.2 试验验证

在Mastercam仿真加工生成的刀具路径基础上，选择JTVC650B立式加工中心作为加工机床，同时选取第3节正交试验中椭球面和马鞍面的最优切削参数和刀具路径，进行曲面分区铣削，本文研究主要集中在半精加工阶段。选用相同的工件(C6061铝合金棒工件)做曲面整体铣削，其中进给率为1 100 mm/min、主轴转速为3 000 r/min，刀具路径分别选用平行铣削、45°平行铣削及流线铣削。半精加工深度ap为0.5 mm,残留高度h为0.06 mm。 曲面分区铣削加工与曲面整体铣削加工的能耗和加工时间对比见表5。工件分别采用曲面分区铣削加工和曲面整体铣削加工所获得半精加工曲面，见图15和图16。

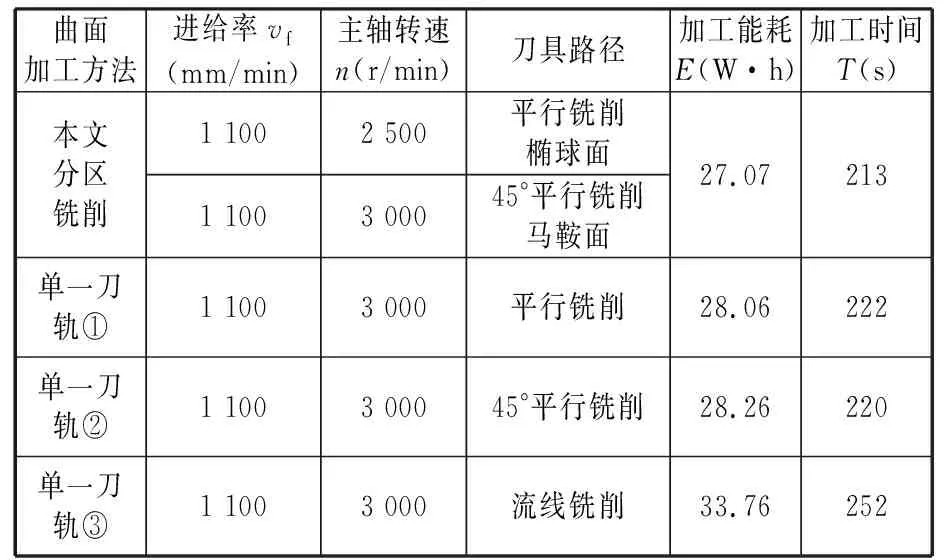
表5 试验结果

图15 曲面分区铣削的半精加工曲面图Fig.15 The semi-finishing surface map of partition milling

由表5的试验结果可以看出：复杂曲面分区铣削加工与复杂曲面采用统一切削参数和刀具路径的加工方式相比，前者能耗最多降低19.8%，最少降低3.5%，平均降低9.1%；曲面分区铣削与曲面整体铣削相比，前者加工时间最多缩短15.4%，最少缩短3.2%，平均缩短7.5%。由此可以说明：复杂曲面分区铣削与复杂曲面整体铣削相比，可有效提高加工效率并降低能耗。

(a)平行铣削 (b)45°平行铣削

(c)流线铣削图16 曲面整体铣削加工的半精加工曲面图Fig.16 The semi-finishing surface map of milling globally

5 结论

针对复杂曲面类零件数控加工过程存在的能耗高、加工效率低等问题，从复杂曲面分区加工的角度出发，提出了面向高效节能的复杂曲面分区加工铣削优化方法。基于复杂曲面的曲率特性，运用FCM算法实现了复杂曲面分区。对于每一个曲面分区，采用正交试验设计求解最优的切削参数和刀具路径，实现能耗和加工时间的综合最优。通过将复杂曲面分区铣削方法与复杂曲面整体铣削方法进行能耗和加工时间对比，验证了所提方法的有效性。所提出的复杂曲面分区铣削优化方法为复杂曲面类零件高效节能数控加工提供了一种新思路，对于降低复杂曲面类零件制造过程的能量消耗、提高加工效率具有重要意义。

本文主要采用试验分析方法确定复杂曲面分区对能耗和加工效率的影响情况，并求解出能耗和加工时间最优的切削参数与刀具路径。下一步将深入研究复杂曲面分区与数控加工能耗、加工效率之间的关联模型，为复杂曲面高效、节能数控加工优化方法提供支持。