熔融沉积成形快速成形机加热构建平台的温度场分析及优化

吕 宁 郑 健 赵 欣 徐 薇

哈尔滨理工大学自动化学院，哈尔滨，150080

0 引言

3D打印作为近年来高速发展的快速成形技术，已经在医疗材料、机械部件成形、模型模具等制造领域得到广泛应用。熔融沉积成形(fused deposition modeling，FDM)技术是3D打印中使用最多的技术,FDM成形过程是在热场内进行的[1]。本文借助Alitum Designer软件对FDM成形的传统加热构建平台(heated build platform,HBP)进行改进设计，并通过FloTHERM软件对HBP进行模拟温度数据分析，形成热场分布图。本文主要研究内容有：①对HBP的工作原理进行分析；②针对传统HBP加热不均匀的现象提出优化设计方案，即利用温度补偿的方式保证HBP整体温度均匀分布；③通过FloTHERM软件完成对传统HBP和优化后的HBP的温度场模拟，形成热场分布云图；④进行打印验证，将相同模型不同HBP的打印效果进行对比，以验证优化和仿真的合理性。

1 HBP的工作原理分析

FDM快速成形机分为封闭型和开放型两种，对于封闭型快速成形机，打印空间与外部温度交换较少， HBP在封闭环境下工作时，温度交换主要集中在打印空间内部，成形期间打印空间内部温差小，对于最终成形件，会一定程度地避免收缩问题。但是对于开放型快速成形机，打印空间与外部空间直接连接，打印空间的温度直接取决于外部空间温度，且HBP也会与外部空间进行大量热交换，导致HBP中心区域与边界区域有温度差，打印过程中对成形件加热不均匀，使得成形件对平台的附着力不同，进而加剧了成形件收缩现象的发生[2]。

PLA(polylactic acid)材料熔点为175～180 ℃，根据实际测量结果，打印温度在202～210 ℃时材料挤出效果最佳，而HBP温度在40～50 ℃时，成形件对打印平台的黏着性最好，不会发生收缩现象。打印过程中最佳温度范围如图1所示。

图1 挤出头和HBP打印温度范围Fig.1 Extrusion head and HBP print temperature range

HBP主要通过电阻热效应来加热，电流通过电阻产生热效应，通常加热功率为240 W，在12 V电压条件下，电阻约为2 Ω，电流为6 A。

HBP的温度控制过程如下：由系统每隔20 ms读取温度传感器上的模拟数值，经过12位模数转换器(analog-to-digital converter,ADC)转换成数字量，再通过系统设定的转换规则将数字量转换为十进制温度值，这个过程通过定时器中断完成；然后将读取得到的温度值和设定的温度值进行比较，最后通过PID控制调节法来输出控制加热电路通断的信号(PWM波)，控制HBP加热的启停，从而对HBP温度进行调控。控制流程如图2所示。

图2 HBP控制系统流程图Fig.2 HBP control system flow chart

2 HBP的温度数值模拟

使用HBP有助于防止翘曲，从而可提高打印质量。被挤出的耗材冷却时会稍微收缩，而当耗材在HBP上进行成形时，材料在成形过程中会保持一定的温度，从而保证材料在熔点以下冷却时更均匀地收缩。使用HBP通常会产生更高质量的成品。市面常见的HBP是PCB_heatedbed_MK2(下文简称MK2)。

HBP需要6A的电流才能工作，在供电电压与3D打印机供电电压相同(即12 V)时，HBP的电阻就要求控制在2 Ω内。在印刷电路板(printed circuit board，PCB)制版时，HBP的电阻完全取决于PCB的敷铜量[3]。MK2往往是将PCB板分为4个区域进行并联分区加热，这样可以使得加热时间缩短。但分区时是将整个PCB板进行四等分，各个区域线长线宽相等，这样也保证了加热时各个区域发热量相等，但是HBP的边界区域相对面积更大，与外界产生的热交换和热传导更多。通过使用红外温度探头对MK2各点温度进行采集，温度差采集结果如图3所示。

图3 HBP温度差曲线图Fig.3 HBP temperature difference graph

MK2基本尺寸为214 mm×214 mm。由温度采集结果可以看出，HBP在加热后表面温度并不是均匀分布的，即HBP并不是以恒定温度对模型进行加热，温度绝对误差为3.2 ℃。FDM成形在本质上是利用高温将材料融化成半流动液态型，根据分层数据控制打印喷头挤出，堆叠形成打印产品[4]。在打印过程中，材料经过挤出头时，温度在200 ℃左右，在HBP上冷却时，由于边界与中心温度不同，导致材料冷却收缩率不同，当HBP绝对温度差过大时，不仅没有避免成形件收缩翘边现象，反而会加剧这种现象发生。对于ABS材料和PLA材料来说，如果要求成形件精度在误差允许范围内，就要求HBP的绝对误差小于1 ℃。

在HBP温度场分析中，由傅里叶热传导定律和能量守恒定律可以得到HBP温度场系统的热平衡方程，即热传导方程：

(1)

式中，ρ为材料密度；c为材料质量热容；T为温度；t为时间；Kx、Ky、Kz分别为x、y、z方向上的热导率；Q为原料凝固释放的热量，其符号放热为正，吸热为负。

系统温度T为恒定值，计算稳态解时

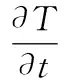
(2)

所以，系统稳态时温度场热量平衡方程为

(3)

计算该公式时需要考虑温度场应用计算中的三种边界条件，分别是：

(1)第一类边界条件。边界面上的温度分布为常数，与时间无关，不随时间t的变化而变化，即

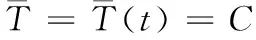
(4)

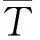
(2)第二类边界条件。在边界面上热流密度已知的情况下，有

(5)

式中，cosx、cosy、cosz分别为x、y、z轴上边界面沿法线的余弦值；φ(t)为热流密度，且为与时间无关的常数，J/(m2·s)。

(3)第三类边界条件。当任意边界面温度已知为Tb时，且已知表面传热系数为h时，此时物体与外界发生热传导，可以用以下公式表示：

(6)

式中，Tf为环境温度。

由于HBP多为热对流方式对热量进行传导和交换，本次模型仿真采用第三类边界条件，所以式(6)可以转换为牛顿冷却公式：

Q=h(Tb-Tf)S=hSΔT

(7)

φ(t)=h(Tb-Tf)=hΔT

(8)

式中,S为接触面积;ΔT为温度差。

从式(7)、式(8)可以看出，HBP与外界进行热量传递的主要影响因素有传热系数h、温度差ΔT和HBP与外界接触面积S，所以，对HBP温度场的优化应从这3个方面进行考虑。

优化前HBP在PCB布线时将供电线分布在HBP的两侧，由于供电线的线宽要远大于发热区域的线宽，相对电阻小，所以边缘区域发热量不足。在实际加热过程中，边缘区域温度就会较中心区域更低，并且通过对优化前HBP温度场仿真和热传导公式推导，验证了优化前HBP等分加热区域对边界面加热效果并不理想，边界面与外界接触的面积更大，热量传递更多，直接导致边界面与中心区域温度差过高，无法满足高精度成形件对精度的要求。根据傅里叶热传导定律和牛顿冷却公式的推论，及传热系数h、温度差ΔT和与外界接触面积S3个影响HBP温度均衡的重要条件，对加热区域重新进行划分，并单独为边界面区域分区。经过验证，通过增加边界面区域的发热量来实现温度补偿是减小HBP温度差的有效方法。图4和图5分别为优化前和优化后HBP的分区加热示意图。

图4 优化前HBP分区加热示意图Fig.4 HBP partition heating diagram before optimization

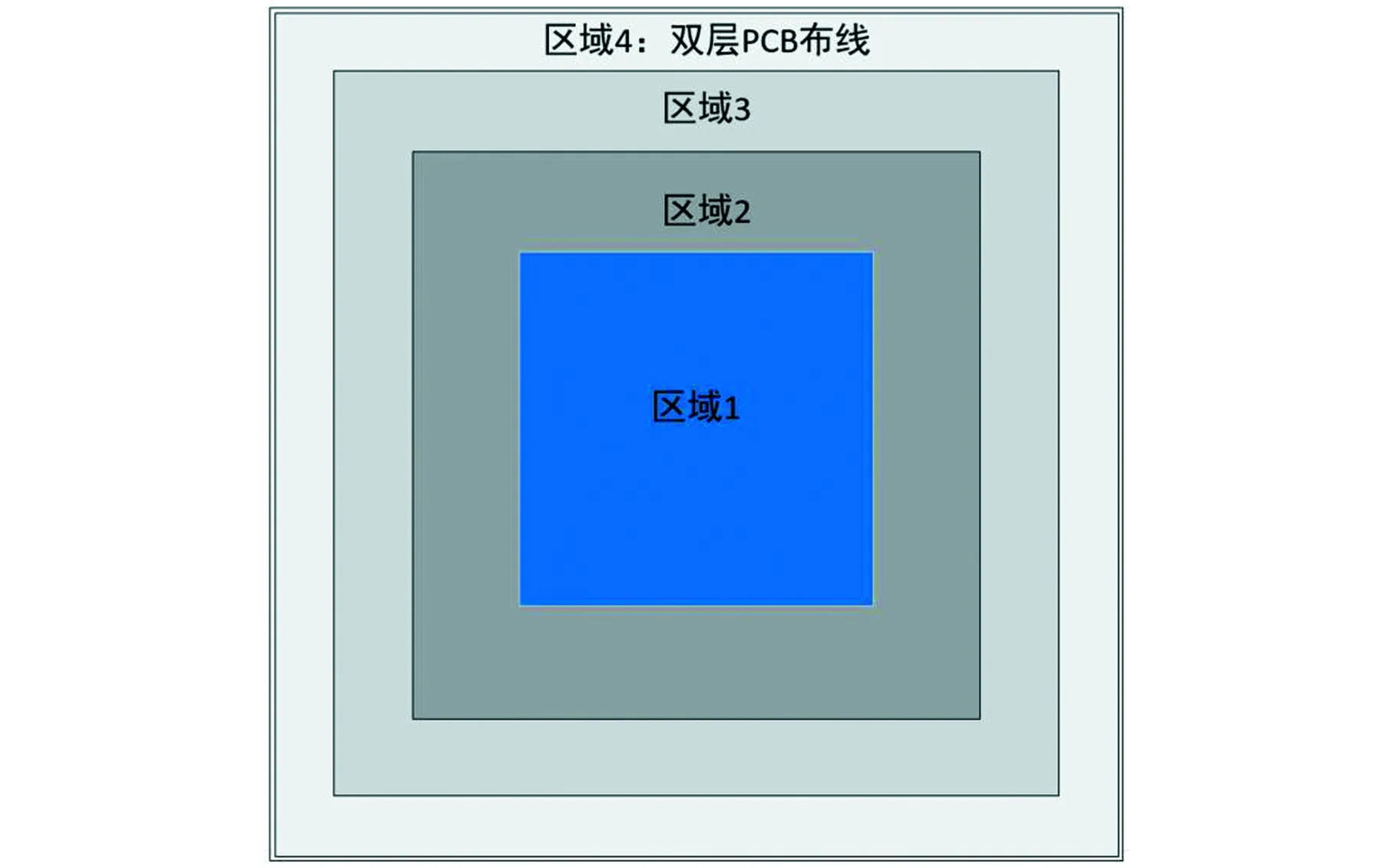
图5 优化后的HBP分区加热示意图Fig.5 HBP partition heating diagram after optimization

通过Alitum Designer重新规划HBP的PCB布线设计，将HBP单层板升级为双层板，将供电线与加热线分离，使得加热区在HBP的面积中占比更高。对区域进行重新划分，单独为边界区域分区，并且通过减小边界区域的线长和线宽，使得边界面区域在加热过程中发热量更高，实现温度一次补偿。

在边界区域(图5的区域4)实行双层布线。正常工作时边界面的双层PCB布线同时工作，实现温度二次补偿，使得HBP各区域温度更为均衡，避免成形过程中材料受热不均匀导致的收缩形变。图6为优化后HBP的PCB布线图。

(a)正面图 (b)背面图图6 优化后HBP的PCB布线正面图和背面图Fig.6 Optimized PCB layout of HBP front view and rear view

3 HBP温度场实验验证

本文通过FloTHERM软件[5]分别对优化前和优化后HBP的PCB模型进行温度场仿真。通过Altium Designer将MK2的PCB模型转化为FloEDA格式导入到FloTHERM中，为了模型的热仿真能尽可能地接近真实值，基于有限单元法对HBP进行网格划分，在网格划分过程中，在保证精度的同时还需要考虑仿真计算速度(即相邻网格之间温度差不超过0.1 ℃)。以此为基准，将设计好的PCB模型导入FloTHERM中，采用FloTHERM的计算流体动力学和数值传热学来解算PCB的温度分布，进行有限元划分。划分后的HBP网格如图7所示，共划分为63 463个单元和102 431个节点。

图7 HBP温度仿真网格划分Fig.7 HBP temperature simulation grid

在完成网格划分后就可以对MK2温度场进行分析计算，由于HBP在正常工作情况下最主要的温度交换方式是热传导和热辐射，所以在选择计算模式时需要选择热辐射计算，环境温度选择为20 ℃。在计算过程中，先进行热辐射交换因子计算，再开始后续的计算工作，运算完成后会生成温度场分布云图，在云图中可以得到计算模型的最高温度、最低温度和详细的温度分布情况[6]。MK2温度分布云图见图8。

图8 环境温度为20 ℃时MK2温度分布云图(优化前)Fig.8 MK2 temperature profile at 20 ℃ ambient temperature(before optimization)

从图8中可以得出，优化前MK2绝对温度差为3.3 ℃，实际测量温差(3.2 ℃)也与仿真结果极为接近，验证了测量和仿真的一致性。在云图中可以更直观地看到由于供电线在MK2的边缘，发热量不足，使得边界面与中心区域形成较大的温差，这对快速成形过程中大体积成形件的模型精度会造成极大影响，严重影响成形精度。

将优化后HBP的PCB模型导入到软件FloTHERM中，分别设置环境温度为0 ℃和20 ℃进行仿真，得到相应的分布云图见图9和图10。

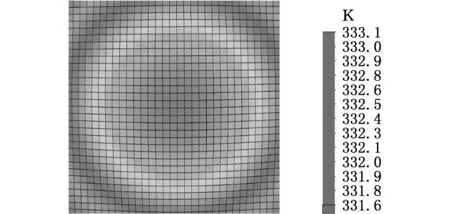
图9 环境温度为0 ℃时MK2温度分布云图(优化后)Fig.9 MK2 temperature profile at 0 ℃ ambient temperature(after optimization)

图10 环境温度为20 ℃时MK2温度分布云图(优化后)Fig.10 MK2 Temperature profile at 20 ℃ ambient temperature(after optimization)

从图9、图10中可以得出，当外界温度为0 ℃时，边界面与中心区域绝对温度差为0.9 ℃，当外界温度为20 ℃时，边界面与中心区域绝对温度差为0.3 ℃，远远小于MK2优化前的温度差3.2 ℃，显著地减小了温度差，使得HBP温度更加均衡。

通过上述对两种HBP温度数值仿真可以看出，优化后的HBP模型在温度均衡性上明显优于优化前的MK2。下面将通过实验对2种不同HBP的打印效果进行验证。实验材料采用直径为1.75 mm的PLA丝材，为了更好地体现HBP对打印效果的影响，选用没有封闭成形室的3D打印机。在正常打印过程中，方形平板模型是最容易产生翘曲变形的模型，方形模型尺寸为80 mm×80 mm×5 mm，模型如图11所示。

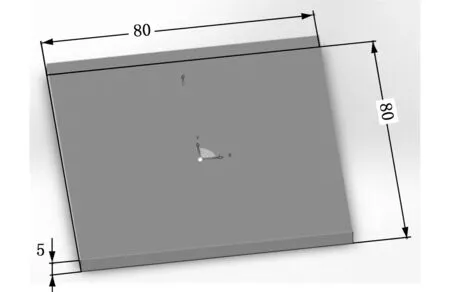
图11 方形平板模型Fig.11 Square tablet model

在打印过程中，为了验证温度对成形精度的影响，需要对FDM快速成形机的HBP温度、挤出头温度、打印速度、喷嘴尺寸等参数进行统一设置，各项参数配置见表1。

表1 设备各项参数表

在环境温度为20 ℃时分别使用不同HBP对矩形平板模型进行打印，将模型的中心分别放在HBP中心、距HBP中心33 mm和距HBP中心67 mm处进行打印。将方形平板模型的4个角分别定义为A、B、C、D点，其中，在距中心33 mm处和距中心67 mm处2种情况下，靠近HBP边缘的2个点为C、D点，靠近HBP中心的2个点为A、B点。A、B、C、D四点位置分别如图12所示。当矩形平板模型在HBP中心处进行打印时，A、B、C、D点位置如图13所示。

图12 测量点位置示意图(距中心67 mm)Fig.12 Location of measuring points (67 mm from the center)

图13 测量点位置示意图(中心位置)Fig.13 Location of measuring points (central location)

打印完成后，分别测量模型各点翘曲量和实际尺寸，与理论模型进行对比。打印后的模型效果如图14所示。实际测量数据见表2。

图14 打印完成模型Fig.14 Print complete model

表2 模型尺寸测量数据

其中，成形件1～6分别是在2种不同HBP的中心位置、距中心33 mm和距中心67 mm处成形，其中距中心67 mm处的2个成形件的CD边与HBP边界面重合。从实验数据可以看出，成形件在实际成形过程中都发生了收缩翘曲变形现象。其中，优化前HBP打印出来的成形件翘曲量明显大于优化后HBP打印出来的成形件翘曲量；距中心67 mm处的成形件由于CD边与HBP边界面重合，翘曲量远大于在HBP中心位置成形件的翘曲量。

在4个角点的形变中，位于中心位置的成形件4个角点翘曲量基本相同，其余成形件的C、D点翘曲量较大，A、B点翘曲量较小，验证了HBP温度不均衡导致了形变的产生，且成形件整体尺寸变小。

4 结语

通过实验可以看出，在减小成形件翘曲变形方面，优化后的HBP要明显好于优化前的HBP，验证了HBP温度是影响成形件收缩的主要原因，并且优化后的HBP在中心位置的成形件形变量极小，成形尺寸与原模型相差无几，大大提高了FDM打印成形精度。然而，成形件收缩变形的根本原因是层间应力，通过优化HBP温度可以有效减小翘曲变形现象的发生，但是无法彻底避免。

在实际成形过程中，还可以通过提高环境温度、减小打印层厚、降低打印速度等方式来更好地对成形件收缩变形进行优化[7]。