广义线性模型下ERIC方法的调节参数选择

王亚荣，白永昕，田茂再，，2b

(1.兰州财经大学 统计学院，甘肃 兰州 730020；2.中国人民大学 a.统计学院；b.应用统计科学研究中心，北京 100872)

一、引 言

当今，在大数据背景下经常会遇到一些高维数据。所谓的高维数据，是指数据的维数会随着样本量大小的不断增加而随之逐渐增长。然而，一个好的回归模型并不是考虑的自变量越多越好，而在建立回归模型时选择变量的基本指导思想是“少而精”；当面对这些高维数据时，如何才能从众多的数据中挖掘出人们关心的且最能体现出整个数据特征的变量，这对该领域的数据分析就显得尤为重要。统计建模目前是处理这类问题最主要的也是最有效的方法之一，但在建模过程中为了保证良好的准确性和解释性需对模型进行变量选择。为此，Fan和Li提出了惩罚的思想，其拟合效果良好，同时还指出一个好的惩罚函数应当使计算出的估计量满足以下三种性质[1]：

1.无偏性：当未知参数的真实值较大时，其系数的估计值应当是几乎无偏的，以避免不必要的模型偏差。

2.稀疏性：估计量应该满足一个阈值规则，能够自动地将系数估计值小的参数设为零，以达到降低模型复杂度的目的。

3.连续性：要求得到的参数估计具有连续性，具有一定的抗随机影响能力，以避免在模型预测时的不稳定性，即变量选择的结果会由于数据集合的微小变化而发生大的变化。

基于这种思想，后续出现了很多基于惩罚最小二乘法的变量选择准则，例如：Hoerl和Kennard提出了岭回归方法[2]；Frank和Friedman提出了桥回归[3]；Tibshirani提出了LASSO(Least Absolute Shrinkage and Selection Operator)惩罚[4]；尤其对于变量个数大于样本数时，该方法明显优于传统最小二乘法和极大似然估计[5]；Fan和Li是在对各种惩罚的研究中提出了SCAD(Smoothly Clipped Absolute Deviation)惩罚；李扬等人提出了污染数据的稳健稀疏成组变量选择方法[6]，以上这些惩罚函数都具有很多优良性质，其中应用比较广泛的就是SCAD惩罚函数，当选择合适的调节参数时它可以很好地选择出正确模型，并且可以同时进行参数估计，一般不会过度压缩参数。最重要的是，该惩罚函数不仅克服了LASSO估计在某些情况下不相合的缺点，而且所得到的估计量具有oracle性质，这种惩罚方法不仅增加了模型的稳定性，而且大大降低了算法的复杂性[7][8]297-307[9]。需要指出的是，该惩罚函数的良好性质取决于调节参数的恰当选择。

在调节参数选择方面，当n→时信息准则AIC(λ)选择调节参数λ时依概率没有欠拟合的现象，即模型中的显著变量将全部被选中，而不会出现遗漏重要参数的情况，但这并不说明AIC(λ)准则所选的就是正确模型，因为AIC(λ)准则将不可避免地出现过拟合的情况，而这种情况并不会随着样本量n的增大而消失。之后，周荣旺提出了在大样本情况下使用MBICu(λ)方法和MRIC方法进行调整参数选择[10]；江河使用广义交叉验证与BIC方法对SCAD惩罚函数进行调节参数的选择，实证结果表明BIC对模型参数的惩罚比GCV强一些，BIC方法选择了一个比GCV方法要大一些的调节参数，并进一步压缩了所选择模型中的参数个数，这样防止了过拟合的出现[11]；Hui等人提出了在自适应LASSO惩罚函数中使用ERIC方法来进行调节参数的选择，并证明了ERIC方法的大样本性质，结果表明ERIC方法在选择真正模型调节参数时远胜过BIC和其他传统的信息准则[12]；崔杰研究了多元广义线性模型基于SCAD惩罚函数的调节参数的选择方法，提出了一个选择调节参数的IC信息准则，该准则结合了AIC准则和BIC准则，证明了在一定条件下该准则选择的模型具有相合性[13]，但是该准则的良好性质是在变量个数p固定的情况下得到的，因此当变量个数发散或者比样本量大的时候该准则将不再适用[13]；家会臣等人指出，Logistic回归模型中交叉验证在小样本时选到真模型的概率更大[14]；陈萌萌指出，可在高维回归中使用组块3×2交叉验证的方法进行调节参数的选择[15]；王天颖等人提出了惩罚交叉验证准则(PCV)，并讨论比较了该准则与其他选择调节参数准则的效果，结果表明在选择变量的准确性方面，该准则比AIC准则、BIC准则、GCV准则都更加有效[16]；罗静等人通过使用广义线性混合效应模型和广义估计方程对空气质量指数进行了分析，即基于广义线性模型将推广的正则化信息准则ERIC(the Extended Regularized Information Criterion)方法应用到SCAD惩罚函数进行调节参数选择，并对相应的大样本性质给出详细的证明过程[17]；Zou和Li使用不同的调节参数选择方法，分别基于Logistic回归模型和Poisson回归模型进行拟合，对比分析各种方法的拟合效果，并将拟合效果较好的ERIC方法应用于实证分析[18]。这里，ERIC准则主要是为了解释应用SCAD惩罚的效果，尤其是当系数不趋于零时的拉普拉斯先验效果，因为在广义线性模型的SCAD惩罚估计中通过ERIC准则选择的调节参数具有选择一致性，这种一致性认为使用ERIC准则选择调节参数比用其他准则有更广泛的适用范围。笔者在SCAD惩罚中使用ERIC准则，借鉴Zou和 Li提出的局部线性近似(LQA)算法进行参数估计，模拟结果表明在真正模型中ERIC准则在选择调节参数时优于其他的选择准则。

二、模型及其SCAD惩罚对数似然函数

(一)广义线性模型

考虑使用如下广义线性模型(GLM)：设y1，y2，…，yn相互独立，且对每个i，yi服从指数分布：

(1)

其中b(·)和c(·)为已知连续函数；θi与φ为未知参数，则称Y=(y1，y2，…，yn)服从指数分布族。期望E(yi)=b′(θi)，方差Var(yi)=b″(θi)φ。当θi=xTβ时，式(1)可改写为：

(2)

其中β=(β1，β2，…，βp)T为回归系数；θi为典则参数，随xi的变化而变化；φ为冗余参数，且通常用于解释方差。满足上式则称Y与x1，x2，…，xP服从广义线性模型。

(二)SCAD惩罚对数似然函数

Fan和Li提出了一种连续可微的SCAD惩罚函数，其形式可构造为：

对SCAD惩罚函数求一阶导数可得到下式：

有了上面的SCAD惩罚函数，就可以写出SCAD的惩罚似然函数。基于式(2)的广义线性模型的对数似然函数形式为：

(3)

因此，基于SCAD惩罚的对数似然函数可写为：

(4)

(三)SCAD惩罚对数似然的参数估计

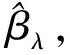
(|βj|2-|βj0|2)βj≈βj0

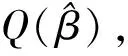
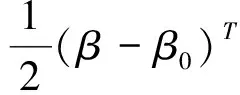
(5)

则迭代解为：

β(k)=β(k-1)-[2l(β(k-1))-n∑λ(β(k-1))]-1

(6)

当算法收敛时，估计应该满足条件：

因此可通过下面的迭代求得式(4)的解：

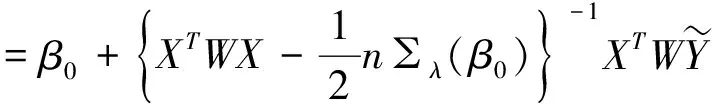
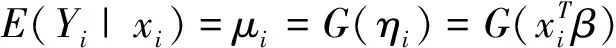
V(μ)=b″(θ)

三、调节参数选择方法

SCAD惩罚函数的优良性质取决于调节参数λ的正确选择，因为不同的调节参数对应于不同的模型，究竟哪个调节参数对应的模型才是最好的，这是一个很重要的问题。调节参数λ的确定，主要还在于选择一个评价模型优劣的准则Crit，而选择Crit的常用方法有CV准则、AIC准则和BIC准则等，但这些传统的选择准则都各有缺陷，要么欠拟合，要么过拟合，因此本文基于比较先进的ERIC方法进行调节参数的选择。这里，给出ERIC信息准则，并将其应用到SCAD惩罚函数中进行调节参数选择，ERIC函数形式如下：

(7)

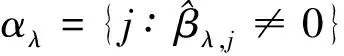
需要特别强调的是，因为模型的复杂性，方法ERICυ(λ)与BIC(λ)有着根本上的区别：BIC(λ)的改进形式更适合高维数据模型，BIC(λ)在每一个新的变量进入模型而惩罚了一个常数值；与此相反，ERICυ(λ)有着动态方差惩罚，且这个动态方差惩罚取决于λ本身。至于大样本情况，ERICυ(λ)假定λ随着样本量的增加而增大，因为基于偏差方差权衡的惩罚效果很重要。

四、渐近性质

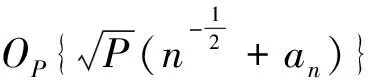
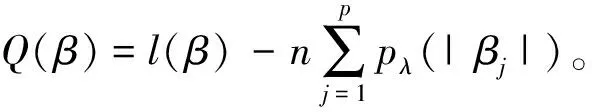
假定1观测Vi独立同分布，f(V,β)为概率密度函数，f的对数求导满足：

(j=1，2，…，p)

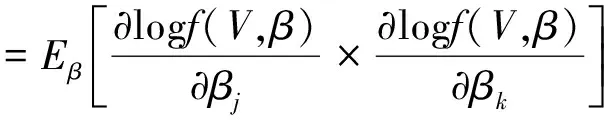
假定2Fisher信息矩阵：

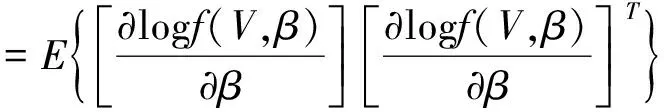
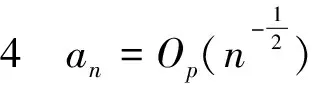
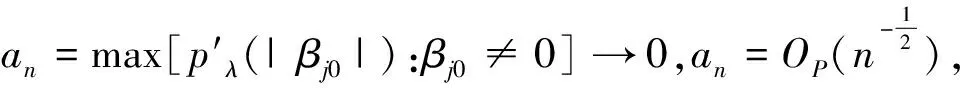
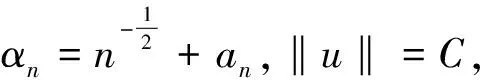
(8)

这就意味着惩罚对数似然函数Q(β)至少以1～ε的概率存在一个局部最大值：

Dn(u)≡Q(β0+αnu)-Q(β0)

≤l(β0+αnu)-l(β0)-

这里αλ是β10的元素个数。令l′(β0)为l的梯度向量，因此：

≜T1+T2+T3

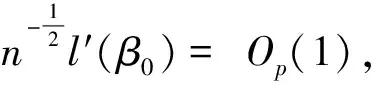
(9)

定理1得证。

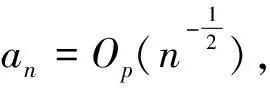
证明：

①：由定理1可得知，当n→时，如果λ→0且，那么任意β1满足‖β1-β10‖=Op(n-1/2)，对任意常数C有：

且ε=Cn-1/2

j=αλ+1，2，…，p

(10)

(11)

这里β*位于β与β0之间，由于：

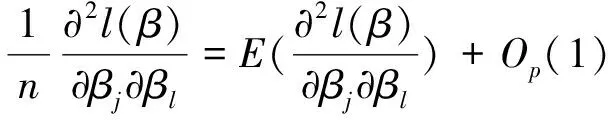
通过假定β-β0=Op(n-1/2)，因此有：

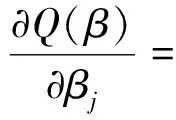
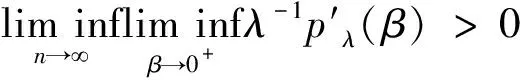
定理2的1)得证。

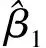
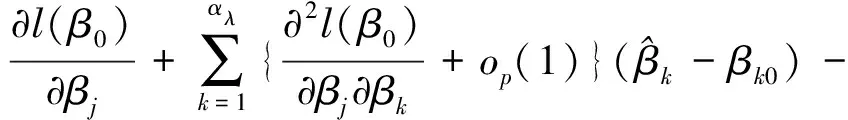
上式满足Slutsky定理和中心极限定理，因此有：

→N(0,I1(β10))

定理2的2)得证。

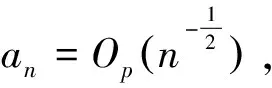
证明：令α0=(j:βj0≠0)为不带惩罚的真实(初始)模型，αλ0为带惩罚的真实(初始)模型，αλ为带惩罚的所选模型，p0=|α0|。

欠拟合模型：Λ-={λ:α0⊄αλ}

正确模型：Λ0={λ:α0=αλ}

过拟合模型：Λ+={λ:α0⊂αλ,α0≠αλ}

带惩罚的ERIC准则记为：

因此记不带惩罚的ERIC准则为：

所以在假定2的条件下，将上述式子用泰勒展开：

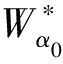
其中A为常数矩阵，因此：

故原式可化为：

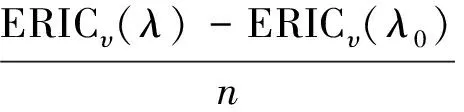
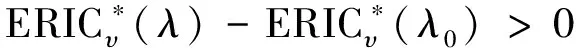
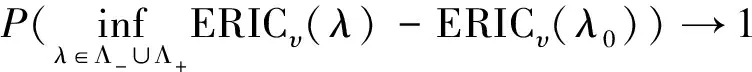
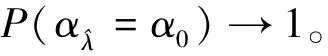
定理3得证。

五、模 拟

那么相对模型误差为：

其中ME为候选模型的模型误差；MEfull为全模型的模型误差；RME为重复试验中候选模型的模型误差ME与全模型的模型误差的比值，称其为相对模型误差；MRME为重复试验中相对模型误差RME的中值，因此本文模拟部分使用MRME作为衡量模型预测优劣的指标。

(一) Logistic回归

假定给定xi，yi服从概率为P(yi=1|xi)=p(xi) 的Bernoulli分布，取：

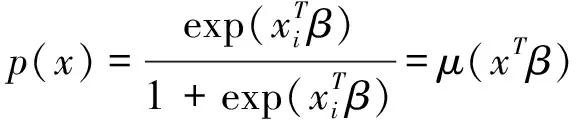
因此式(4)可写为：

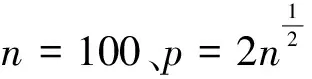
模拟结果如表1所示，Oracle表示用参数真值计算的结果，表中欠拟合、正确拟合、过拟合分别表示500次重复试验中预测模型的欠拟合概率、正确拟合概率、过拟合概率，而MRME为重复试验中相对模型误差RME的中值。

在整个模拟过程中可明显发现，CV方法计算速度比较慢，耗时较长，消耗大量计算资源，并且拟合效果不理想。

表1 Logistic回归模拟结果表

从表1模拟结果可以看出，随着样本量n的增大或者相关系数ρ的减小，ERIC方法的相对模型误差中值MRME比CV、AIC、BIC准则的MRME都小；当ρ=0.25、n=400且ERIC1时，MRME值为0.174，已经非常接近真实模型的MRME值，即Oracle值0；当ρ=0.25且n=400时，ERIC能够选择出正确模型的概率分别为76.6%和83.8%，特别是ERIC1为83.8%，比较接近理想概率1，拟合效果较好，可见υ=1时的ERIC更适合样本量较大时的情形。

下面是当n=400且ρ=0.25时，ERIC0.5(λ)和ERIC1(λ)准则选择调节参数λ时的箱线图(见图1)。

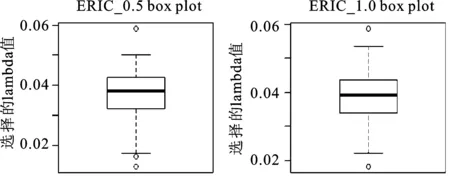
图1 ERIC准则选择的调节参数λ值箱线图

从图1可以看出，由ERIC准则选择的调节参数λ的分布表现的还是比较均匀的，尤其是右侧的ERIC1(λ)箱线图；左侧的ERIC0.5(λ)箱线图略微负偏(下侧的须较上侧的须略长)，而右侧ERIC1(λ)箱线图分布就比左侧的ERIC0.5(λ)更显均匀。图1中小圆圈表示的是可能的离群点的观测。

(二)Poisson回归

假定给定xi，yi服从均值为λ(xi)的Poisson分布，则λ(xi)=exp(xTβ)=μ(xTβ)，因此式(4)可写为：

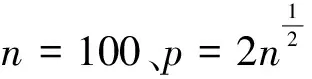
从表2可以看出，随着样本量n的增大或者相关系数ρ的减小，ERIC方法选择正确模型的概率以及相对模型误差中值比其他三种方法表现较好，但是相对模型误差中值相差不大，在相同的样本量和相关系数下，模型误差中值MRME仅有微小的差别。尽管ERIC准则与其他准则相比表现略好，但是与Oracle值相差还是比较大，没有在Logistic回归中拟合得好。

下面是当n=400且ρ=0.25时，ERIC0.5(λ)和ERIC1(λ)准则选择调节参数λ时的箱线图。由于Poisson分布产生的随机数据是离散的，且经常会存在一些特别大或者特别小的异常值，这种离群的表现，导致箱子整体被压缩得很扁，有时甚至只剩一条线。因此，鉴于调节参数取值为正数，可尝试对其做对数变换。图2是对数变换后所得箱线图。

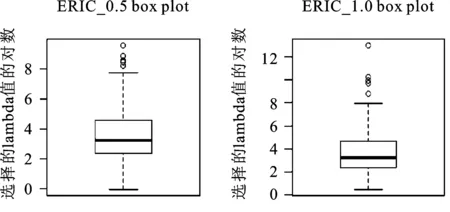
图2 ERIC准则选择的调节参数λ值取对数后箱线图

从图2可以看出，由ERIC准则选择的调节参数λ的分布表现得虽然没有在Logistic回归中那么均匀，波动程度略大且略微有点正偏(上侧的须较下侧的须略长)，但从整体来看调节参数λ的分布也还算均匀。

六、实证分析

本节利用广义线性模型下的SCAD惩罚函数对一组实际数据进行调节参数的选择和参数估计，并且分析相关结果。

(一)数据描述

以南德国银行的信用评分数据为例。利用SCAD惩罚对该组数据进行变量选择及建模分析，研究各指标与信用评分Y之间的关系，其中调节参数的选择使用文章提出的ERIC方法；数据中包含1000家客户信用数据，其中700名客户信用好，300名客户信用不好，每个客户在数据中有如下属性：

Y：信用质量(buen表示信用好，mal表示信用不好)

Cuenta：信用客户的银行质量(no表示没有，good running表示信用好，bad running表示信用差)

Mes：账户的月份

Ppag：先前账户的支付情况(buen表示好，mal表示不好)

Uso：使用目的(privado表示私用，profesional表示公用)

DM：设计手册中的信贷额度

Sexo：性别(hombre表示男性，mujer表示女性)

Estc：婚姻状况(vive solo表示单身，no vive solo表示其他)

这里试图从分析该组数据来确定影响该银行的信用评分指标。

(二)数据处理

通过对数据的初步观察，发现信用客户的银行质量Cuenta是多分类离散变量，因此这里引入虚拟变量X11和X12，其中X11表示信用好的账户，X12表示信用差的账户，这样有助于检验不同的属性类型对因变量信用质量Y的作用；信用质量Y是分类变量，因此分析之前需先将因变量Y转化为二值型的0～1变量，0表示信用不好，1表示信用好，然后储存为矩阵的形式；除此之外还有变量Ppag、Uso、Sexo、Estc也做同样的变化，分别用X4、X5、X7、X8表示；其次使用Logistic模型研究自变量X对因变量Y的影响，最后计算该模型基于ERIC准则的调节参数选择及选择后的参数估计。

(三) ERIC信息准则的调节参数选择

由于模拟部分不论是在Logistic模型中还是Poisson模型中都显示出当υ=1时ERIC方法的相对模型误差中值较小，且表现较好，因此数据整理好之后，本节就使用υ=1时的ERIC方法对该组数据进行调节参数的选择以及选择后的参数估计，分析结果见图3。

图3 ERIC准则选择的调节参数λ值的箱线图

从图3可以看出，由ERIC方法选择的调节参数λ的分布比较均匀(下侧的须与上侧的须几乎一样长)。图3中小圆圈表示的是可能的离群点的观测。

表3 SCAD惩罚下使用ERIC准则进行调节参数的选择及参数选择后的估计表

注：*表示显著性程度。

由表3所得结果可以看出，所选择的模型没有设计手册中的信贷额度X6、性别X7和婚姻状况X8，说明设计手册中的信贷额度X6、性别X7和婚姻状况X8对客户的信用的好坏几乎没有影响；而影响信用好坏的主要因素是信用好的账户X11、信用差的账户X12、账户的月份X3、先前账户的支付情况X4、使用目的X5这几个变量；这里调节参数的选择过程是先给出一系列λ值，然后计算其对应的ERIC值，最后选择出令ERIC值最小的λ值作为最优的调节参数。表3显示选择的最优调节参数λ为0.0112，对应的ERIC值为62.241 5。