线矢力各向同性分析与其在机构构型综合中的应用

2019-02-15许允斗郭金伟王志峰姚建涛赵永生

农业机械学报 2019年1期

许允斗郭金伟王志峰陈阳姚建涛赵永生

(1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛 066004； 2.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004； 3.首都航天机械有限公司，北京 100076)

0 引言

线矢力是指被约束在方向、位置固定的直线上的矢量[1]，它是力螺旋的一种特殊形式，在基于螺旋理论的少自由度并联机构自由度分析[2-3]及构型综合[4-6]中发挥了重要的作用，在六自由度并联机构的奇异位形分析[7-9]及各向同性六自由度并联机器人的设计[10]方面也有一定的应用。除此之外，尚无线矢力在并联机构其他方面的应用研究报道。机构的承载能力也直接与线矢力相关，如3-PRRR三自由度移动并联机构[11]3条支撑分支输入运动副对动平台施加的3个驱动线矢力(输入运动副所产生的约束线矢力)之间的各向同性[12]决定了机构的承载性能(P为移动副，R为转动副)。因此，线矢力的各向同性是其重要的性能指标。

然而，现有文献对线矢力各向同性的研究较少，文献[10,13-15]研究如何布置各测量分支使得并联机构六维力传感器达到力和力矩各向同性，该类型传感器每个测量分支向测量平台施加一个沿着分支轴线的约束线矢力，所以每个测量分支实际上相当于一个线矢力。除此之外，尚无其他对线矢力自身各向同性性能进行分析的报道。文献[16-18]对三自由度移动并联机构的构型综合进行了研究，并已得到了很多新构型。但这些文献的对象均为非冗余驱动三自由度移动并联机构，即输入运动副数目等于自由度数，目前对有冗余驱动三自由度移动并联机构尚未见报道。然而，冗余驱动在承载能力的提高方面[19-21]起到了至关重要的作用，如国内外几种典型的大型农业机械[22-23]均采用冗余驱动并联机构以有效地提高其承载能力，所以冗余驱动三自由度移动并联机构具有良好的应用前景。

此外，现有文献综合三自由度移动并联机构时并未考虑机构的承载性能，即不考虑由各输入运动副引起的驱动线矢力之间的几何关系。因此，本文结合线矢力的各向同性分析，对冗余驱动三自由度移动并联机构进行构型综合时，先考虑各驱动线矢力的几何关系，以得到承载能力各向同性的冗余驱动三自由度移动并联机构。

1 线矢力各向同性分析

本文分析仅当线矢力相交于一点的情况。在交点处建立一个参考坐标系OXYZ，设相交于一点的n条线矢力在该坐标系的Plücker坐标为

(1)

式中 (ai,bi,ci)T——第i条线矢力的方向矢量

一般情况下，为满足各向同性，各线矢力在空间应呈对称分布，则可设n条线矢力均匀分布在一锥面上，如图1所示。n条线矢力的Plücker坐标可写为

(2)

其中

α=2π/n

式中θ——线矢力所在锥面的锥顶角的一半

α——各相邻线矢力在水平面投影的夹角

由于各线矢力均通过坐标原点，线矩始终为零，故将其省略。

图1 线矢力在空间上的分布Fig.1 Spatial distribution of line vector forces

将各线矢力的Plücker坐标写成矩阵形式

(3)

为了使各线矢力满足各向同性，则矩阵M的条件数应等于1，即矩阵M的最大奇异值和最小奇异值的比值为1。由矩阵分析理论可知，矩阵M的奇异值恰好等于MMT矩阵特征值的开方，MMT可表示为

(4)

经分析可知，该矩阵前(n-3)个特征值为零，故要求MMT矩阵的最后3个特征值相同，结合MMT特征矩阵的行列式，可以求得使MMT矩阵满足最后3个特征值相同时锥顶角的一半θ为54.736°。比如，当线矢力数目为4时，即n=4，则α=π/4，故4个线矢力组成的矩阵为

(5)

此时该矩阵3个奇异值均为1.154 7，故4条线矢力满足各向同性，如图2所示。

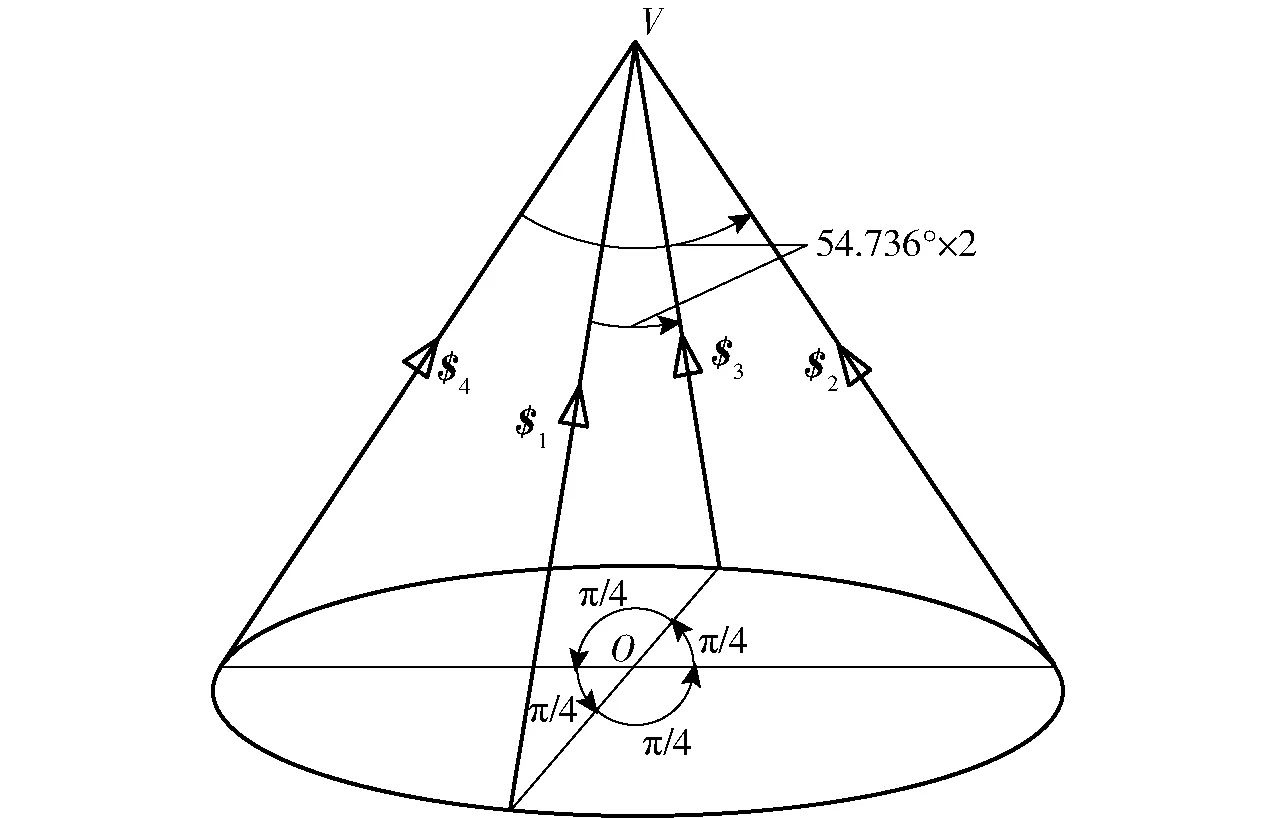
图2 4条线矢力满足各向同性时的分布Fig.2 Distribution of four isotropic line vector forces

当线矢力分布在一平面内时，此时是空间情况的一种特殊情形，即当圆锥顶点在底面时，则圆锥上均匀分布的线矢力处于一平面内，此时它们也满足各向同性条件。如空间线矢力数目为4时，投影到平面恰好为分布在两条坐标轴上的4条线矢力，显然满足各向同性条件。

2 冗余驱动三自由度移动并联机构构型综合

2.1 基于螺旋理论的约束综合法基础

根据反螺旋理论[1]可知，支链末端施加给动平台的结构约束力螺旋，与该支链的所有运动副的运动螺旋互易。机构末端约束力螺旋系为所有支链结构约束力螺旋组成的螺旋系，该约束力螺旋系决定机构的自由度。由文献[4-6,24]可知，并联机构型综合过程为首先根据机构要求的末端运动螺旋系求出其末端约束力螺旋系，然后构造支链约束力螺旋系，求出支链运动螺旋系构造支链机械结构，最后配置这些支链机械结构形成符合要求的并联机构。

2.2 基于螺旋理论的约束综合法冗余驱动三自由度移动并联机构构型综合

关于少自由度并联机构构型综合的研究，一般情况下当得到并联机构构型后，需添加驱动副，并判断所添加驱动副是否合理[25-26]。为了得到满足预期承载能力要求的机构，本文先考虑驱动副的类型与布置。此时，就需要考虑各驱动副产生的驱动力螺旋的几何关系，还需考虑驱动力螺旋与约束力螺旋之间的关系。驱动力螺旋是指支链的驱动运动副施加给动平台的力螺旋，它与该支链中除驱动副外其他所有运动副互易。

这里只构造冗余驱动数目为1的对称冗余驱动三自由度移动并联机构，即驱动副数目为4，4个驱动副对称分布在4条支链中。则每个分支施加给动平台的约束力螺旋可以是1、2或3个约束力偶，驱动副施加给动平台的驱动力螺旋是一个线矢力，这里将结合前面得到的线矢力各向同性条件使4条支链施加给动平台的4个驱动线矢力达到各向同性，即构造各向同性冗余驱动三自由度移动并联机构。

首先根据支链施加动平台的约束力偶和驱动线矢力构造支链除驱动副外的其他运动副组成的运动链，该运动链的运动螺旋系与分支约束力偶和驱动线矢力均互易；然后构造与约束力偶互易且与驱动线矢力不互易的驱动副。

表1满足支链约束力偶和驱动线矢力要求的典型运动链
Tab.1Typicalkinematicchainssatisfiedexpectedrequirementofconstraintcouplesandactuationforce

图3 典型各向同性冗余驱动三自由度移动并联机构构型(1)Fig.3 Typical isotropic redundantly actuated 3-DOF translational parallel mechanisms(1)

图4 典型各向同性冗余驱动三自由度移动并联机构构型(2)Fig.4 Typical isotropic redundantly actuated 3-DOF translational parallel mechanisms(2)

3 冗余驱动三自由度移动并联机构承载能力分析

(6)

图机构的结构简图Fig.5 Structural diagram of PM

设动平台中心O在参考坐标系VXYZ坐标为(x,y,z)T，各支与动平台连接点bi(i=1,2,3,4)在参考坐标系VXYZ下坐标分别为

(7)

设各支链与定平台的连接点为ai，由于支链自身的结构约束，可知ai与bi坐标在各自支链移动副轴线ri上的投影相等，则可得到ai坐标在ri上的投影值为

(8)

令各支链驱动P副的输入为qi，则可得

(9)

式中a0——初始位置各支链连接定平台的铰链点沿P副轴线的位移

对式(9)两边求时间的导数，可得输入速度与动平台速度之间的关系为

(10)

式中J——将动平台速度映射到输入速度的速度雅可比矩阵

由虚功原理[27]可得外力与各支链驱动力之间的关系为

(11)

式中F——外力

τi——支链i提供的驱动力

假设各驱动副的承载能力极限值均为τmax，则可求得该机构在X、Y和Z主方向的承载能力极限值均为2.309 4τmax[28]，而且JT是一个常数阵，表明该机构在运动过程中始终是满足承载能力各向同性的。由此表明，在构型综合时考虑了驱动线矢力的各向同性，综合得到的机构也是满足承载能力各向同性的。因此，也一定程度上验证了关于线矢力各向同性的分析以及对冗余驱动三自由度移动并联机构的综合理论是正确的。