基于混合蛙跳优化的采摘机器人相机标定方法
2019-02-15陈科尹邹湘军关卓怀彭红星吴崇友
陈科尹 邹湘军 关卓怀 王 刚 彭红星 吴崇友
(1.农业农村部南京农业机械化研究所, 南京 210014; 2.贺州学院信息与通信工程学院, 贺州 542899; 3.华南农业大学南方农业机械与装备关键技术省部共建教育部重点实验室, 广州 510642)
0 引言
相机标定是采摘机器人进行视觉识别与定位的重要前期步骤之一。相机标定精度在很大程度上决定了后续目标识别定位的准确性。因此,找到一种精度高、稳定可靠的相机标定方法显得格外重要。目前,比较常见的相机标定方法是基于张正友相机标定原理,利用计算智能优化算法对其进行改进[1-7]。YAO等[1]利用遗传算法BP神经网络对张正友相机标定方法进行改进;FÜHR等[2]在张正友相机标定方法的基础上,提出了一种基于非线性优化的相机自标定方法;PITCHANDI等[3]结合张正友相机标定方法,利用遗传算法对视觉辅助机器人装配系统的相机标定问题进行了研究;ZHANG等[4]基于张正友相机标定方法,提出了一种基于线段的柔性在线相机标定方法;游江等[5]提出了基于改进遗传模拟退火的相机标定方法;柯丰恺等[6]提出了基于凸松弛优化算法的相机内外参数标定方法;刘艳等[7]针对鱼眼镜头存在的畸变问题,对张正友相机标定法进行了改进。
但此类基于张正友相机标定原理改进的相机标定方法还存在以下问题[8-9]:在求取相机标定参数初值时,先不考虑相机畸变因素,直接利用平面靶标图像中的特征点线性求解相机标定参数初值。但实际上这些特征点存在的畸变误差会影响相机标定参数初值的准确性。在考虑相机畸变因素、进一步优化相机标定参数时,采用了非线性优化过程,若相机标定参数初值选择不当,容易收敛到局部最小,从而影响相机标定参数的精度以及稳定性。平面靶标图像数量直接影响相机标定参数的精度和稳定性。基于张正友相机标定原理的本质是通过建立平面靶标图像中特征点的世界坐标与像素坐标之间的映射关系方程组,根据最小二乘方法,求取相机标定参数。显然,通过增加平面靶标图像数量,即可增加特征点的世界坐标与像素坐标之间映射关系方程组的数量,从而提高最小二乘方法求取相机标定参数的精度。但随着平面靶标图像数量的不断增加,在同等标定环境下特征点的提取和畸变等误差也不可避免地带入相机标定过程,从而影响相机标定参数的精度和稳定性。
为此,按照对采摘机器人相机标定精度的要求(相机焦距的绝对误差在0.1~1 mm内,相对误差在1%~15%内;平面靶标图像特征点的平均像素误差在1个像素内;双目相机之间距离的绝对误差在1~5 mm内,相对误差在1%~6%内),本文拟引进混合蛙跳优化算法和LM算法对采摘机器人相机标定,进行定量研究。同时,为验证本文相机标定方法的有效性和可靠性,分别同传统张正友相机标定方法(OpenCV库自带)、基于遗传算法的相机标定方法以及基于标准混合蛙跳算法的相机标定方法进行相机标定性能对比试验。
1 相机标定
1.1 张正友相机标定原理
张正友相机标定原理[10]是通过移动相机或平面靶标(标定板),从不同的方位采集平面靶标图像,利用平面靶标上特征点的图像坐标和其已知的三维空间坐标(Z坐标置为0)的对应关系,计算出相机模型参数的初始值,然后再进行非线性优化,从而完成相机标定操作。其具体相机标定过程如图1所示。
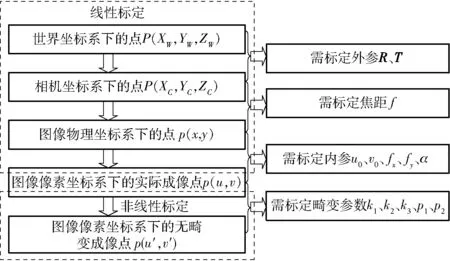
图1 张正友相机标定原理的相机标定过程Fig.1 Camera calibration process with Zhang Zhengyou’s camera calibration principle
图1中,R为相机外参旋转矩阵,T为相机外参平移向量,f为相机焦距,u0为相机内参光心横向像素坐标,v0为相机内参光心纵向像素坐标,fx为相机内参焦距横向像素,fy为相机内参焦距纵向像素,α为相机内参成像平面倾角,k1、k2、k3为相机径向畸变参数,p1、p2为相机切向畸变参数。
1.2 基于改进混合蛙跳算法和LM算法的相机标定原理
张正友相机标定方法,一般先直接求取相机模型的参数初值,然后利用LM算法对该参数初值进一步非线性优化求精,从而求出最终的相机模型参数。但是,直接求解相机模型参数初值的计算过程非常繁琐,并且由于LM算法自身固有的特点,该类相机标定方法对相机模型的参数初值非常敏感,从而使标定出的相机模型参数很不稳定。
本文结合混合蛙跳优化算法以及LM算法各自的特点,对张正友相机标定原理,进行以下几点改进:直接运用最小二乘法求取单应性矩阵,不必要利用LM算法对其进行优化,简化了求取单应性矩阵的过程。运用混合蛙跳优化算法来求取相机模型参数初值,避免直接求取相机模型的参数初值所带来的繁琐计算和LM算法对参数初值敏感的问题。运用改进LM算法对相机模型的参数初值进行优化处理,避免了原LM算法必须求取需要优化参数的雅可比矩阵,从而造成优化过程中出现不稳定现象。
1.2.1混合蛙跳优化算法
混合蛙跳优化算法[11-13]是模仿青蛙觅食过程中的群体信息交互机制而建立的一类智能计算优化算法。该优化算法结合了模因(Meme)演算法和粒子群优化算法各自的优点,具有概念简单、控制参数少、计算量小、全局寻优能力强、鲁棒性好、易于实现等特点。为此,选取该优化算法来求取相机模型的参数初始值。其基本原理可描述为:
假设L={F1,F2,…,FN}为N只青蛙组成的初始种群;其中,Fi={xi1,xi2,…,xiS}为所求问题的S维解空间中的第i只青蛙。并且,将该种群内的青蛙个体按适应值降序排列。接着把整个种群划分为m个模因组,第1只青蛙划入第1个模因组,第2只青蛙划入第2个模因组,第m只青蛙划入第m个模因组,第m+1只青蛙划入第m+1个模因组,依此类推,直至种群内所有青蛙分配完毕。
同时,把每一个模因组内具有最好适应值和最差适应值的青蛙分别标记为Fb和Fw,而该种群中具有最优适应值的青蛙标记为Fg。然后,对模因组内的每一个青蛙执行局部位置更新操作,具体更新公式为
(1)
式中r——0~1之间的随机数
D——青蛙移动的距离
⟸——位置更新操作
Dmax——青蛙所允许移动的最大距离
如果更新后得到的青蛙优于原来的青蛙,则可替代原模因组内的青蛙Fw;否则,用Fg代替Fb,执行局部位置更新操作
(2)
如果式(2)操作仍然不能获得更好适应值的青蛙或移动过程中超过了青蛙所允许的最大移动距离,那么就随机生成一个新的青蛙直接替代原来的Fw。重复数次以上局部位置更新操作,并将所有模因组内的青蛙重新混合排序和划分模因组,再执行下一轮的数次局部位置更新操作,直到满足预先设定的收敛条件或者达到混合最大迭代次数为止。
为了加快混合蛙跳优化算法的收敛速度和减少其局部位置更新操作的次数,本文在文献[14-15]的基础上,对其稍作些修改:对其局部位置更新操作,引入加速因子。仅需执行一次局部位置更新操作,取消多次重复执行该操作。修改后的混合蛙跳算法的局部位置更新操作为
(3)
式中c——加速因子
若更新后得到的青蛙优于原来的青蛙,则可替代原模因组内的青蛙Fw;否则,用Fg代替Fb,执行局部位置更新操作
(4)
如果式(4)等操作仍然不能获得更好适应值的青蛙或移动过程中超过了青蛙所允许的最大移动距离Dmax,那就随机生成一个新的青蛙直接替代原来的Fw。
修改后混合蛙跳优化算法的具体实现过程为:
(1)初始化相关参数,在所求问题的定义域内随机产生N只青蛙,构成一个初始种群,并置模因组数为m,模因组内的青蛙个数为n,使其满足N=m×n;置混合最大迭代次数为G。
(2)计算每只青蛙的适应值,并按照其适应值的大小降序排列、选出该种群中具有最优适应值的Fg和划分模因组。
(3)选出每个模因组的Fb,依据式(3)和式(4),执行局部位置更新操作,更新每个模因组的Fw。
(4)判断混合迭代次数是否达到G或者是否符合预先设定的收敛条件,如果不满足,则返回步骤(2)继续执行;如果满足,则结束算法,输出Fg,即所求问题的解。
1.2.2改进LM算法
相机模型参数的非线性优化,一般可归纳为非线性最小二乘问题。LM算法是解决该类问题较为有效的方法[16]。但是,LM算法需要求取优化参数函数的雅可比矩阵。而相机模型的优化参数函数往往都很复杂,很难通过偏导方法求取其雅可比矩阵。为此,本文采用文献[17]提出的改进LM算法,把原LM算法采取求偏导方式来获取优化参数函数的雅可比矩阵替换为通过求差商方式来获取。
一般非线性最小二乘问题,都可构造目标优化函数
(5)
其中f(X)=[f1(X)f2(X) …fm(X)]T
fi(X)=fi(x1,x2,…,xn)
X=(x1,x2,…,xn)T
式中X——需要优化的参数向量
xi——需要优化的参数(i=1,2,…,m)
改进LM算法的具体步骤可描述为:
(1)给出需要优化的参数向量的初值X(1),初始化阻尼系数c、放大系数β(一般凭经验可取c=0.01,β=10)、允许误差ε,并计算出F(X(1))。
(2)令c⟸c/β,并且计算出需要优化的参数向量f(k)及其雅可比矩阵Ak。
f(k)=[f1(X(k))f2(X(k))…fm(X(k))]T
(6)

(7)
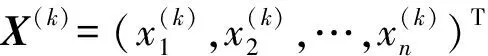
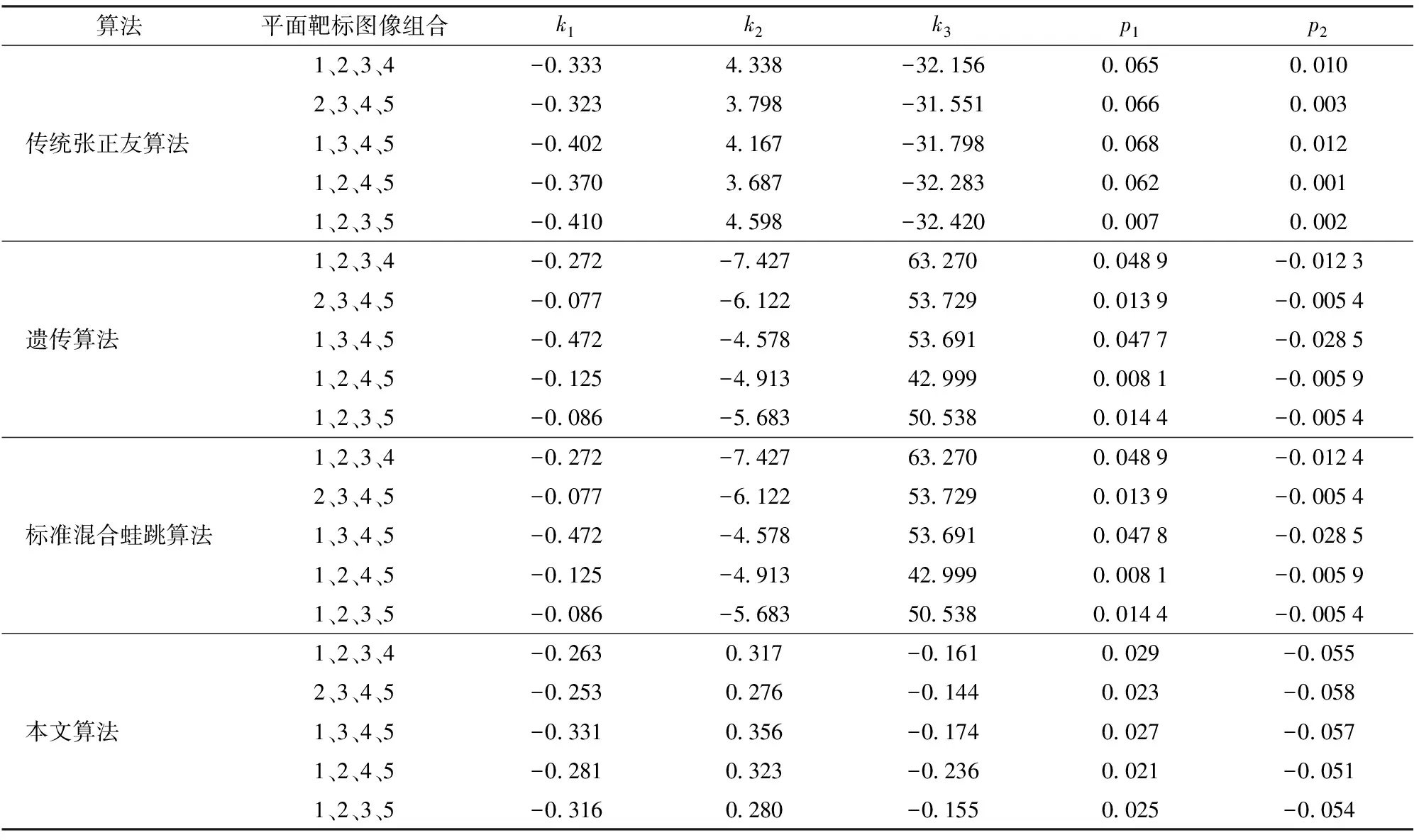
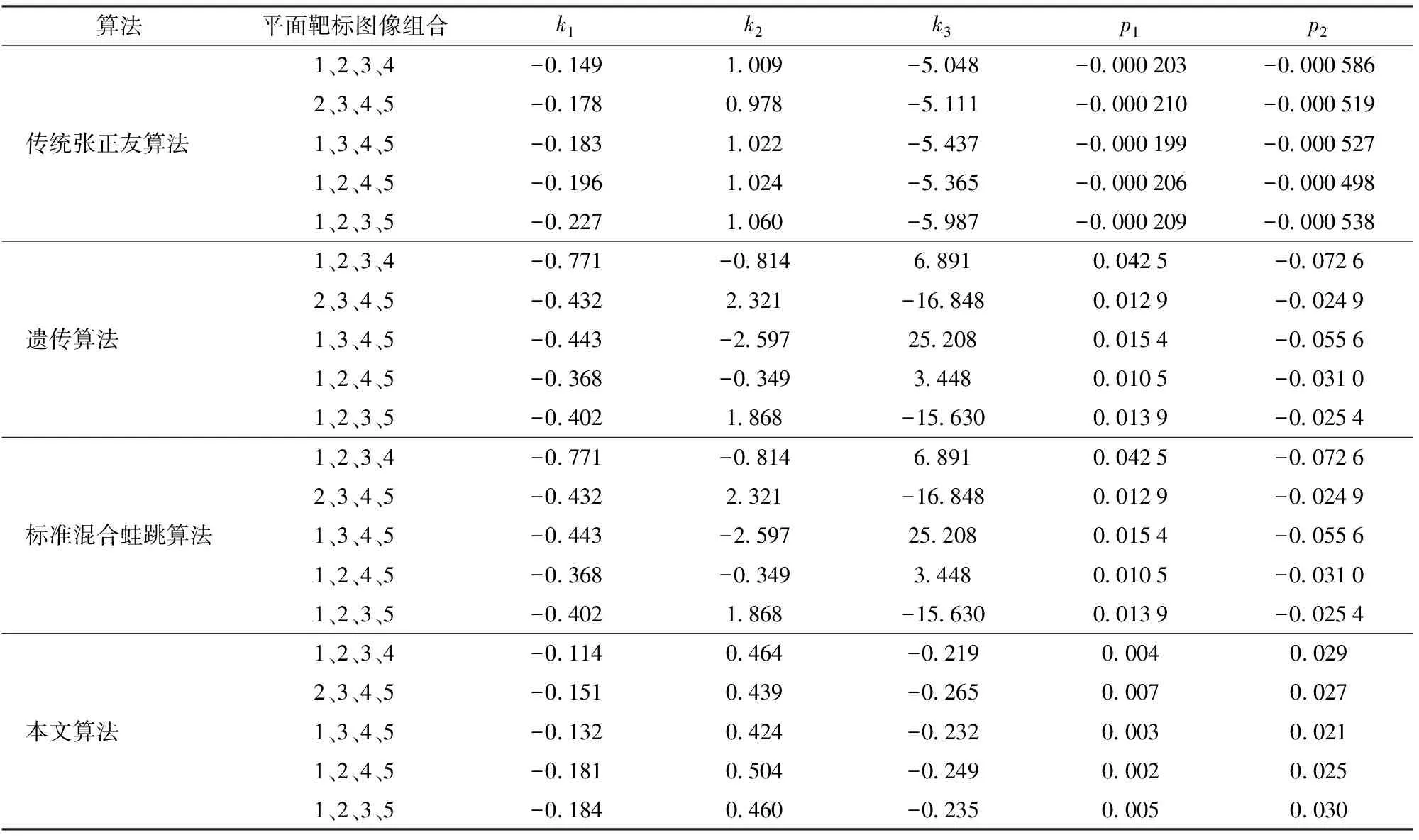
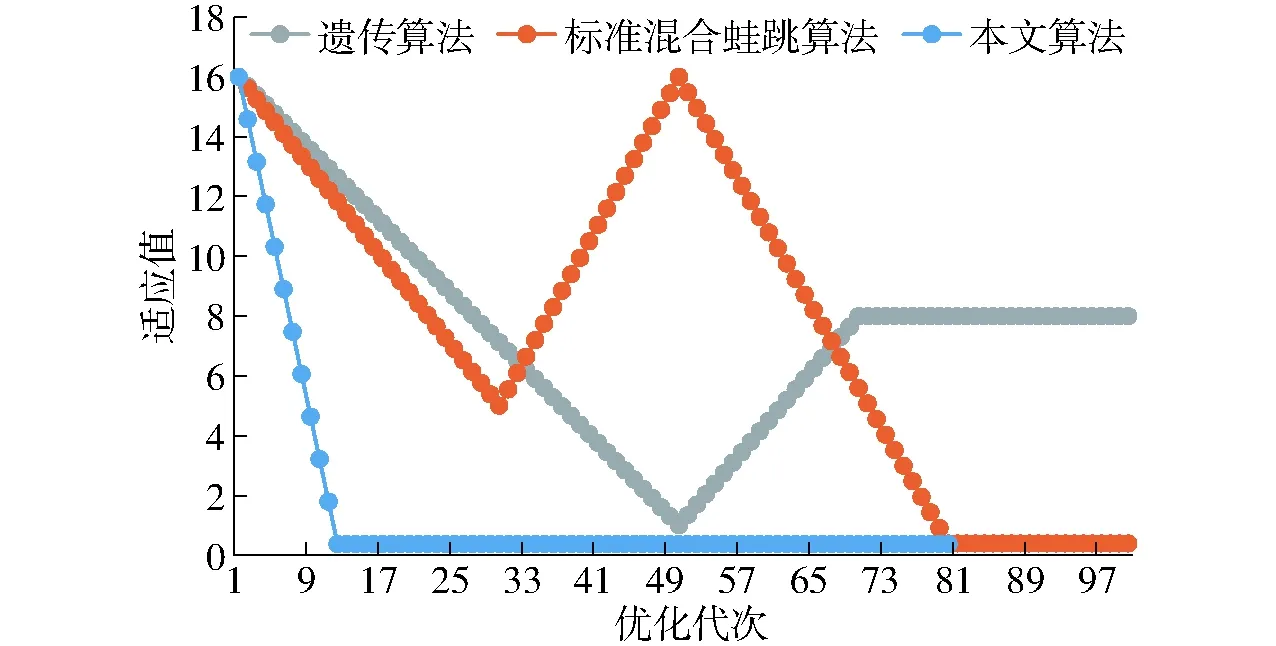
(4)计算F(X(k+1)),如果F(X(k+1)) 1.2.3结合混合蛙跳和改进LM算法的相机标定 参照张正友相机标定原理,结合混合蛙跳优化算法和改进LM算法的各自优点,把相机标定过程划分为以下两步:第1步,以混合蛙跳算法为工具,求出相机模型参数的初始值。第2步,以改进LM算法对第1步求出的相机模型参数的初始值,进一步非线性优化求精,最终求得标定精度较高的相机模型参数。 一般相机模型需要标定的参数包括:内部参数(fx,fy,α,u0,v0)、外部参数(R,T)和畸变参数(k1,k2,k3,p1,p2)。而外部参数求取公式为 (8) 式中K——相机模型的内参数矩阵 H——单应性矩阵 h1、h2、h3——H的第1、2、3列向量 s——比例系数 r1、r2、r3——R的第1、2、3列向量 改进LM算法对相机参数非线性优化目标函数定义为平面靶标图像的二维重投影误差 (9) 式中Iij——第i幅平面靶标图像上第j个特征点在图像像素坐标系下的坐标 Pij——第i幅平面靶标图像上第j个特征点的三维世界坐标 L——平面靶标图像数 M——单幅平面靶标图像特征点数 为了减少混合蛙跳算法的搜索维数,本文仅利用混合蛙跳算法来寻求相机模型的内部参数和畸变参数,而每一幅平面靶标图像的相机模型外部参数由式(8)来求取。为此,依据混合蛙跳算法的原理,可以把每一只青蛙个体表示为 (10) 式中Fk——第k只青蛙个体 显然,又可把混合蛙跳算法的每个模因组内具有最好适应值和最差适应值以及整个种群中具有最优适应值的青蛙个体表示为 (11) (12) (13) 并依据二维图像特征点与三维空间点之间的二维重投影误差和混合蛙跳算法的特点,求取青蛙个体适应值函数 (14) 基于改进混合蛙跳和LM算法的相机标定详细步骤为: (1)提取所有平面靶标图像特征点图像像素坐标系下的二维坐标,同时根据平面靶标图像特征点的二维坐标以及其三维世界坐标,利用最小二乘法直接求取每幅平面靶标图像的单应性矩阵H。 (15) 式中 rand()——0~1之间的随机函数 Wk、Hk——平面靶标图像的宽度和高度 (4)选出每个模因组Fb,依据式(3)和式(4),执行局部位置更新操作,更新每个模因组Fw。 (5)判断混合迭代次数是否达到G或者是否达到预先设定最小适应值η,如不满足,则返回步骤(3)继续执行;如满足,则转到步骤(6)。 1.2.4双目相机立体标定 由于采摘机器人采用双目相机视觉系统,所以不仅需知左、右相机模型的内、外参数,还需知左、右相机之间的对应关系(即左、右相机之间的旋转矩阵和三维平移向量)。 其具体的求解过程为先按照前面介绍的相机标定方法,分别单独求出左、右相机模型的参数,然后依据左、右相机之间的对应关系,求出左、右相机之间的旋转矩阵Rlr和三维平移向量Tlr[18-20]。 假设三维空间中的任意一点P,在世界坐标系、左相机坐标系以及右相机坐标系下的非齐次坐标分别为XW、XCl、XCr,则有 (16) 式中Rl、Tl——左相机模型的外部参数旋转矩阵和三维平移向量 Rr、Tr——右相机模型的外部参数旋转矩阵和三维平移向量 整理式(16),可得 XCl=RlrXCr+Tlr (17) 根据采摘机器人视觉定位精度的要求(视觉定位位置绝对误差0.1~1 mm,相对误差1%~10%)以及双目视觉系统的标定原理,本文设计了由1个三角架、2个出厂参数相同的广角相机(出厂焦距参数f为3.5 mm,像元横向物理尺寸dx为4.65 μm,像元纵向物理尺寸dy为4.65 μm,两个相机主光心之间距离即双目相机之间距离为60 mm)和平面靶标(平面靶标方格的边长为25 mm)组成的采摘机器人双目相机标定试验平台(图2)。 图2 双目相机标定试验平台Fig.2 Test platform of binocular camera calibration 运用OpenCV2.3.1、VS2008和OpenGL编程实现了采摘机器人双目视觉标定系统,见图3。该标定系统包括OpenCV自带的传统张正友相机标定方法、基于遗传算法的相机标定方法(设置交叉概率p为0.8,变异概率q为0.2,优化阈值t为0.5,种群大小N为50,最大迭代次数G为100)、基于标准混合蛙跳算法的相机标定方法(设置加速因子c为0.5,优化阈值t为0.5,种群大小N为50,模因组大小m为5,模因组组内青蛙个数n为10,最大迭代次数G为100)和基于改进混合蛙跳和LM算法的相机标定方法(即本文相机标定方法,设置加速因子c为0.5,优化阈值t为0.5,种群大小N为50,模因组大小m为5,模因组组内青蛙个数n为10,最大迭代次数G为100)。按照图4所示的试验流程,在室外进行相机标定试验。 图3 采摘机器人双目视觉标定系统Fig.3 Binocular camera calibration system of harvesting robot 图4 相机标定试验步骤流程Fig.4 Test procedures of camera calibration 为了评价以上相机标定方法的性能,本文根据误差理论,设计了以下评价指标。 相机焦距绝对误差 ferr=|f*-f| (18) 其中 f*=(fxdx+fydy)/2 式中f*——由相机内部参数fx、fy以及相机像元尺寸参数dx、dy计算出的相机焦距 相机焦距相对误差 fΔerr=|(f*-f)/f*|×100% (19) 平面靶标图像特征点平均像素误差 (20) 双目相机间距绝对误差 (21) tlr——实际的双目相机间距(本文中为60 mm) 双目相机间距相对误差 (22) 同时,考虑到随着平面靶标图像数量的增加,在同等标定环境下,平面靶标图像的特征点的提取误差和畸变误差也不可避免地带入相机标定过程,从而影响相机标定参数的精度和稳定性。为此,本文不选择通过采集大量平面靶标图像进行相机标定试验,而是根据张正友相机标定方法至少所需平面靶标图像数量的要求:只需4幅不同的平面靶标图像,即可完成相机内、外参数标定,左、右相机分别采集5幅不同的平面靶标图像,具体见图5、6。 图5 左相机采集到的5幅平面靶标图像Fig.5 Fine capturing planar target images of left camera 图6 右相机采集到的5幅平面靶标图像Fig.6 Fine capturing planar target images of right camera 然后,利用左、右各5幅平面靶标图像中的4幅图像的不同组合进行相机标定,并依据相机焦距绝对误差、相机焦距相对误差、平面靶标图像特征点的平均像素误差、双目相机间距的绝对误差以及双目相机间距的相对误差的性能评价指标,对以上相机标定方法进行性能评价。具体相机标定参数结果和性能评价结果,见表1~5。 为了比较基于遗传算法的相机标定方法、基于标准混合蛙跳算法的相机标定方法和本文相机标定方法的收敛性,分别统计了100次标定优化过程中适应值的变化趋势,结果见图7、8。 对比表1、2,可知在以上5组不同组合相机标定试验中,传统张正友相机标定方法获得的左相机焦距绝对误差ferr为0.340~0.637 mm,焦距相对误差fΔerr为6.660%~15.406%,平面靶标图像特征点的平均像素误差perr为0.167~0.176像素,右相机焦距绝对误差ferr变化范围为0.237~0.997 mm,焦距相对误差fΔerr变化范围为6.346%~22.181%,平面靶标图像特征点的平均像素误差perr为0.105~0.115像素;基于遗传算法的相机标定方法获得的左相机焦距绝对误差ferr为0.458~3.724 mm,焦距相对误差fΔerr为11.574%~51.552%,平面靶标图像特征点的平均像素误差perr为0.113~0.129像素,右相机焦距绝对误差ferr为1.101~8.654 mm,焦距相对误差fΔerr为23.935%~71.203%,平面靶标图像特征点的平均像素误差perr为0.120~0.181像素;基于标准混合蛙跳算法的相机标定方法获得的左相机焦距绝对误差ferr为0.455~2.155 mm,焦距相对误差fΔerr为11.521%~38.115%,平面靶标图像特征点的平均像素误差perr为0.115~0.131像素,右相机焦距绝对误差ferr为0.771~3.419 mm,焦距相对误差fΔerr为18.053%~49.416%,平面靶标图像特征点的平均像素误差perr为0.120~0.144像素;本文相机标定方法获得的左相机焦距绝对误差ferr为0.065~0.506 mm,焦距相对误差fΔerr为1.899%~12.652%,平面靶标图像特征点的平均像素误差perr为0.166~0.175像素,右相机焦距绝对误差ferr为0.083~0.360 mm,焦距相对误差fΔerr为2.429%~11.484%,平面靶标图像特征点的平均像素误差perr为0.103~0.114像素。 对比表3、4可知,在以上5组不同组合的相机标定试验中,传统张正友相机标定方法获得的左相机畸变参数k1为-0.410~-0.323,k2为3.687~4.598,k3为-32.420~-31.551,p1为0.007~0.068,p2为0.001~0.012,右相机畸变参数k1为-0.227~-0.149,k2为0.978~1.060,k3为-5.987~-5.048,p1为-0.000 210~-0.000 199,p2为-0.000 586~-0.000 498;基于遗传算法的相机标定方法获得的左相机畸变参数k1为-0.472~-0.077,k2为-7.427~-4.578,k3为42.999~63.270,p1为0.008 1~0.048 9,p2为-0.028 5~-0.005 4,右相机畸变参数k1为-0.771~-0.368,k2为-2.597~2.321,k3为-16.848~25.208,p1为0.010 5~0.042 5,p2变化范围为-0.072 6~-0.024 9;基于标准混合蛙跳算法的相机标定方法获得的左相机畸变参数k1为-0.472~-0.077,k2为-7.427~-4.578,k3为42.999~63.270,p1为0.008 1~0.048 9,p2为-0.028 5~-0.005 4,右相机畸变参数k1为-0.771~-0.368,k2为-2.597~2.321,k3为-16.848~25.208,p1为0.010 5~0.042 5,p2为-0.072 6~-0.024 9;本文相机标定方法获得的左相机畸变参数k1为-0.331~-0.253,k2为0.276~0.356,k3为-0.236~-0.144,p1为0.021~0.029,p2为-0.058~-0.051,右相机畸变参数k1为-0.184~-0.114,k2为0.424~0.504,k3为-0.265~-0.219,p1为0.002~0.007,p2为0.021~0.030。 表1 不同相机标定方法获得的左相机标定内参结果及性能评价指标Tab.1 Left camera calibration results and evaluation index with different camera calibration methods 表2 不同相机标定方法获得的右相机内参标定结果及性能评价指标Tab.2 Right camera calibration results and evaluation index with different camera calibration methods 表3 不同相机标定方法获得的左相机标定畸变结果Tab.3 Left camera calibration distortion results with different camera calibration methods 表4 不同相机标定方法获得的右相机标定畸变结果Tab.4 Right camera calibration distortion results with different camera calibration methods 表5 不同相机标定方法获得的双目相机标定结果及性能评价指标Tab.5 Binocular camera calibration results and evaluation index with different camera calibration methods 图7 左相机标定过程中的适应值变化曲线Fig.7 Variation curves of adaptive value in calibration of left camera 图8 右相机标定过程中的适应值变化曲线Fig.8 Variation curves of adaptive value in calibration of right camera 在表5中,Tx为双目相机之间平移向量的X方向分量,Ty为双目相机之间平移向量的Y方向分量,Tz为双目相机之间平移向量的Z方向分量;φx为双目相机之间旋转角向量的X方向分量,φy为双目相机之间旋转角向量的Y方向分量,φz为双目相机之间旋转角向量的Z方向分量。 由表5可知,传统张正友相机标定方法获得的双目相机之间平移向量的分量Tx、Ty、Tz分别为-57.297~-56.577 mm、-57.355~-56.149 mm、-57.391~-55.646 mm,双目相机之间旋转角向量的分量φx、φy、φz分别为2.112~3.718 rad、2.447~3.482 rad、-1.210~-0.911 rad,双目相机间距绝对误差tlrerr为2.703~3.423 mm,相对误差tΔlrerr为4.717%~6.050%;基于遗传算法的相机标定方法获得的双目相机之间平移向量的分量Tx、Ty、Tz分别为-58.933~64.252 mm、-44.215~41.508 mm、-410.380~1 909.058 mm,双目相机之间旋转角向量的分量φx、φy、φz分别为3.273~5.784 rad、-3.728~4.510 rad、-1.356~0.845 rad,双目相机间距绝对误差tlrerr为1.067~124.252 mm,相对误差tΔlrerr为1.810%~274.972%;基于标准混合蛙跳算法的相机标定方法获得的双目相机之间平移向量的分量Tx、Ty、Tz分别为-97.527~-22.735 mm、-5.635~63.765 mm、-133.680~271.134 mm,双目相机之间旋转角向量的分量φx、φy、φz分别为2.770~5.843 rad、1.996~3.412 rad、-0.028~0.502 rad,双目相机间距绝对误差tlrerr为0.175~37.527 mm,相对误差tΔlrerr变化范围为0.290%~163.910%;本文相机标定方法获得的双目相机之间平移向量的分量Tx、Ty、Tz分别为-58.134~-57.211 mm、-0.231~-0.204 mm、-4.868~-4.531 mm,双目相机之间旋转角向量的分量φx、φy、φz分别为1.949~2.735 rad、2.231~3.098 rad、-0.116~-0.108 rad,双目相机间距绝对误差tlrerr为1.866~2.789 mm,相对误差tΔlrerr为3.209%~4.874%。 由此可见,对于左、右相机焦距的绝对误差和相对误差变化,本文相机标定方法最小,传统张正友相机标定方法次之,基于遗传算法的相机标定方法和基于标准混合蛙跳算法的相机标定方法变化较大;对于平面靶标图像特征点的平均像素误差变化,虽然基于遗传算法的相机标定方法和基于标准混合蛙跳算法的相机标定方法稍微小些,但跟传统张正友相机标定方法以及本文相机标定方法的差异不大,都在1像素之内。而相机畸变参数,按照文献[3],认为合适的变化范围为-1~1,但以上4种相机标定方法,除了本文相机标定方法所获得的所有畸变参数均符合-1~1的变化范围外,其余的相机标定方法所获得的畸变参数k2、k3、p1、p2均不在此变化范围之内,且变化也相对较大。而双目相机间距绝对误差和相对误差,基于遗传算法的相机标定方法最大,分别达到124.252 mm和274.972%;基于标准混合蛙跳算法的相机标定方法也相对较大,分别达到37.527 mm和163.910%;传统张正友相机标定方法相对较小,而本文相机标定方法最小。 同时,比较图7、8,可以看出本文相机标定方法的左、右相机标定,适应值随着优化次数增加而下降,分别经过约26次和12次优化后,收敛到一个稳定的适应值;基于遗传算法的相机标定方法的左、右相机标定,适应值先下降后上升,最后分别经过约86次和71次优化后,才收敛到一个稳定的适应值;基于标准混合蛙跳算法的相机标定方法的左、右相机标定,适应值先下降再上升后又下降,最后分别经过约86次和81次优化后,才收敛到一个稳定的适应值。显然可见,本文相机标定方法的收敛速度和稳定性,均优于基于遗传算法的相机标定方法和基于标准混合蛙跳算法的相机标定方法。 以上分析表明,本文相机标定方法所获得的左、右相机内参数fx、fy、α、u0、v0,畸变参数k1、k2、k3、p1、p2和双目相机参数Tx、Ty、Tz、φx、φy、φz均比以上其他3种相机标定方法更为准确可靠。这是因为传统张正友相机标定方法是通过对单应性矩阵奇异值分解来求取相机内参初值,然后利用LM算法对该相机内参数进一步求精。但矩阵奇异值分解存在数值不稳定,并且LM算法优化结果的精度取决于参数初始值,这样将影响求取的相机内参数的最终精度。而基于遗传算法的相机标定方法、基于标准混合蛙跳算法的相机标定方法和本文相机标定方法,先采用仿生智能优化策略直接求取相机内参数初值,避免了对单应性矩阵奇异值分解所造成的相机内参数初值不准确,再利用改进LM算法进一步优化相机内参数,避免了原LM算法优化过程必须求取优化参数的雅可比矩阵所导致求取参数精度的不稳定。但这些仿生智能优化算法本质是基于概率统计规律的随机搜索,随机性很强,面对求取相机内参数这样多元参数非线性优化问题,极容易陷入局部极值,从而造成相机内参数精度不稳定以及优化收敛过程过于缓慢。而本文相机标定方法对标准混合蛙跳算法的局部位置更新操作进行了改进,协调其全局搜索和局部开采的能力,提高了其收敛速度,避免了求取相机内参数初值陷入局部极值的问题,所以本文相机标定方法求取相机内参数比基于遗传算法的相机标定方法以及基于标准混合蛙跳算法的相机标定方法更为准确可靠。此外,因为标准混合蛙跳算法比遗传算法的全局搜索能力强,所以它求取的相机内参结果比基于遗传算法的结果理想。同时,由于相机畸变参数和双目相机参数,是在相机内参数基础上求取的,所以相机内参数的准确性将直接影响相机畸变参数和双目相机参数的准确性。由于本文相机标定方法所求取的相机内参数比其他3种相机标定方法结果均更为准确,因此,本文相机标定方法所求取的相机畸变参数和双目相机参数也相对更为准确可靠。 根据对采摘机器人相机标定精度的要求,针对传统张正友相机标定方法存在标定结果不稳定、容易陷入局部极值等缺点,提出了一种基于改进混合蛙跳和LM算法的相机标定方法。该相机标定方法只需4幅不同平面靶标图像即可完成相机标定,并且相机焦距的绝对误差、相对误差,平面靶标图像特征点的平均像素误差,双目相机间距绝对误差、相对误差等相机标定性能评价指标都符合采摘机器人相机标定精度的要求。标定所获得的左、右相机内参数、畸变参数以及双目相机之间的参数,均优于传统张正友相机标定、基于遗传算法的相机标定和基于标准混合蛙跳算法的相机标定等方法。同时,在相机标定优化过程中,只需很少次优化,即可收敛到稳定的适应值,具有较高的收敛速度和稳定性,能够满足采摘机器人双目视觉定位系统的要求,是一种精度高且简便的相机标定方法。

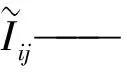

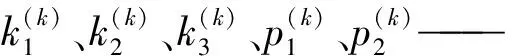
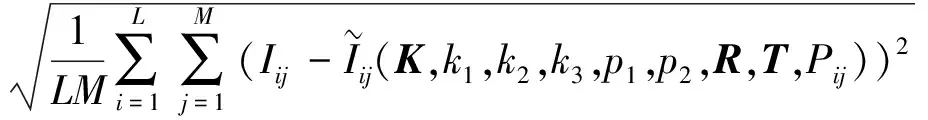


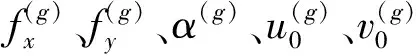
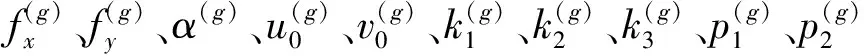
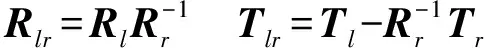
2 试验与结果分析











3 结束语
