八自由度机械臂位置运动学模型解析解

覃艳明 赵静一 仝少帅 王建军

(燕山大学机械工程学院， 秦皇岛 066004)

0 引言

随着科学技术的发展，机器人[1]得到越来越广泛的应用。作为机器人主要执行装置的机械臂则成为机器人技术的重要研究课题。我国是农业大国，农业是国民经济的基础，农业装备则是现代农业的重要支撑。农业机器人是一种以农产品为操作对象、兼有人类部分信息感知和四肢行动功能、可重复编程的柔性自动化或半自动化设备[2-4]。

目前国内学者对机器人在农业方面的应用进行了大量的研究[5-8]。由于农业机器人在执行任务过程中需要避障功能，所以一般采用冗余自由度机械臂。八自由度农业机器人机械臂为冗余机构，其运动学反解存在无穷多组解，求解比较困难[9]，目前均采用数值解求解各关节变量值，计算效率低下。因此，本文以八自由度农业机器人机械臂为研究对象，采用反变换的方法求解机械臂逆运动学的解析解，为该类农业机器人控制的轨迹规划及智能化作业提供依据。

1 机械臂结构

采用SolidWorks对农业机器人的机械臂进行三维建模，它是具有8个自由度的关节机器人，其中2个关节为移动副，6个关节为转动副。根据各部分的三维几何关系进行建模，按顺序将三维模型进行装配，可得到农业机器人的装配体，如图1所示。

图1 八自由度农业机器人三维模型Fig.1 Three-dimensional model of 8-DOF agricultural robot1.基座 2.铰座 3、9.液压缸 4.大臂内管 5.旋转机构 6.回转油缸 7.小臂 8.连接件 10.大臂外管

2 正运动学分析

农业机器人具有8个关节，根据机械臂结构，采用D-H法[10-14]进行各关节坐标系的建立。先确定机械臂的初始位姿，根据此位姿建立基础坐标系和各关节的坐标系。为了简化计算，将关节1的坐标系与基础坐标系重合，之后依次在各关节上建立坐标系，所得机构简图和各关节坐标系如图2所示。

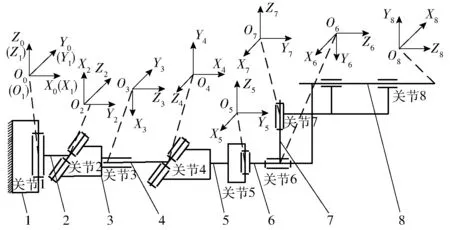
图2 机械臂各关节坐标系Fig.2 Arm joint coordinate system1.基座 2.铰座 3.大臂外管 4.大臂内管 5.连接件 6.旋转机构 7.末端摆动 8.末端装置

正运动学求解就是已知各个关节变量的值，计算机械臂的末端相对于基础坐标系的位置的姿态。根据各连杆参数以及所建立的坐标系的关系可得出各关节的D-H参数表，如表1所示。表中θ1、θ2、d3、θ4、θ5、θ6、θ7和d8为关节变量。

根据建立的坐标系以及D-H参数表可计算各连杆的齐次变换矩阵。由坐标系{i+1}至坐标系{i}的齐次变换矩阵为

表1 八自由度农业机器人的D-H参数Tab.1 8-DOF agricultural robot D-H parameters

(1)

农业机器人有8个自由度，故有8个相邻坐标系的齐次变换矩阵，可分别求得

由上述各关节的齐次变换矩阵可得机械臂的末端位姿矩阵为

(2)

式中前3列向量分别为末端坐标系{8}的X、Y、Z轴在基础坐标系中的方向矢量，第4列为末端坐标系原点在基础坐标系中的位置矢量。

将各关节变量的初值代入式(2)可得出机器人机械臂的初始位姿矩阵

(3)

3 逆运动学分析

逆运动学求解就是已知机械臂末端相对于基础坐标系的位置和姿态，求解各个关节变量的值。逆运动学求解有多种方法，如PAUL等[15]提出的反变换法，LEE等[16]的几何法，PIEPER等[17]的方法等。没有唯一确定的机器人逆运动学求解的方法，本文采用反变换法(也称代数方法)对农业机器人进行逆运动学求解。

由于有8个自由度，但能列出的等式仅有6个，考虑到机械臂为冗余机构，在空间操作时可有效躲避障碍物，另外机械臂在工作过程中小臂需垂直于工作面，则可约束关节2和关节4在工作过程中有θ2-θ4=-180°，关节1和关节5在工作过程中有θ1+θ5=-90°。添加2个约束条件后，机械臂在空间操作过程中可有效地躲避障碍物和优化工作空间。因关节8是一个末端移动关节，在实际工作过程中只需前7个关节确定姿态后，末端在其轴线方向上移动即可，故在运动学分析时可令末端不移动，即d8为定值，取d8=1 775 mm，这样虽然减少了机构的自由度，但不影响机械臂实际的工作过程，有利于计算[18]。为了书写方便，下面表达式中令cosθi=Ci和sinθi=Si，下文atan(y,x)是双变量反正切函数。由式(2)可得

θ6=±arccosoz

(4)

(5)

由式(5)可求得

(6)

进而求得

θ5=-90°-θ1

(7)

θ7=atan2(-S5，C5C6)±atan2(q1,q2)

(8)

其中

(9)

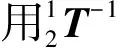
(10)

由式(10)可求得

(11)

其中

(12)

由θ2-θ4=-180°可得

θ4=θ2+180°

(13)

进而求得

d3=-C1S2(px-axd8)-S1S2(py-ayd8)-
C2(pz-azd8)+140S2-420S4C5S6+745S4S5-
134.4S4-420C4C6-96C4

(14)

上述求得的各关节变量共有16组解，根据各关节在实际工作时的取值范围和工作环境，可舍去的解有θ1的第2组解、θ7的加号组解、θ2的加号组解，最后剩余的只有两组解，即

(15)

(16)

依据“最优原则”，当向机械臂末端左边旋转时，采用第1组解，θ6取负号，即旋转机构逆时针旋转，如图3a所示；当向右边旋转时，采用第2组解，θ6取正号，即旋转机构顺时针旋转，如图3b所示。

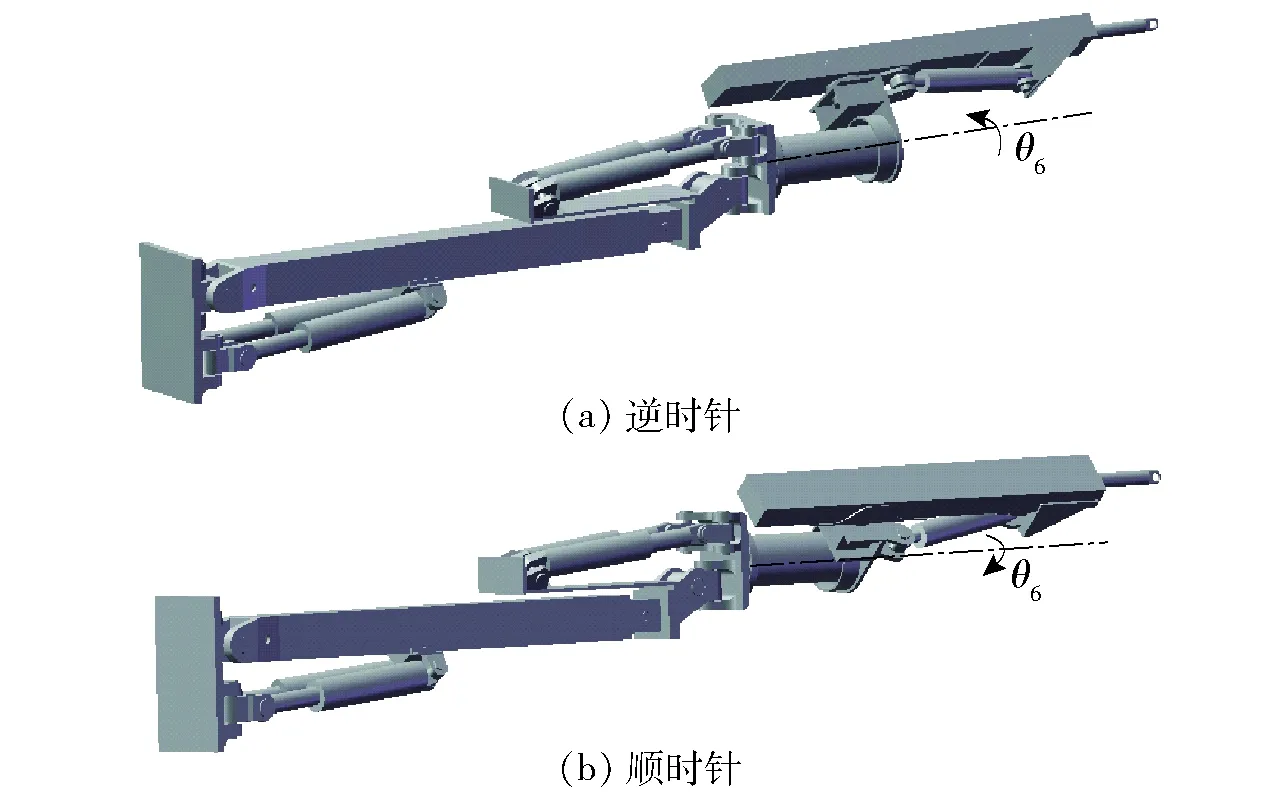
图3 旋转位形Fig.3 Rotation bitmap

4 仿真验证

利用Matlab软件对正运动和逆运动求解仿真进行验证。将正运动和逆运动算法输入到Matlab中，从D-H参数表中各关节变量的取值范围中任意取值，将其代入编写的Matlab正运动程序中，求得末端位姿矩阵，将此位姿矩阵代入逆运动程序中进而求得各关节变量的值，与开始输入量进行比较，以验证仿真结果。为了更加直观地观察机械臂各部分运动情况，可导入到ADAMS中建立仿真模型[19-20]。利用逆运动求解公式可计算各关节变量的值，输入到仿真模型中进行仿真，与理论分析进行对比，验证其正确性。

将机械臂的三维模型导入到ADAMS中，各关节变量值的初值为[0° -90° 2 808 mm 90° -90° 0° 0° 1 775 mm],可得各关节在基础坐标系下的初始位姿如图4所示。

图4 仿真模型中的初始位姿Fig.4 Initial pose in simulation model

给定一组各关节变量值输入到Matlab正运动程序中，可得末端位姿矩阵为

(17)

将式(17)作为已知量代入到Matlab逆运动程序中，可求得两组解分别为[9.999 8° -95.000 0° 3 000 mm 84.999 8° -100.000 4° -30.002 9° 0° 1 775 mm]和[17.093 2° -94.841 3° 3 097.8 mm 85.158 7° -107.093 2° 30.002 9° 0° 1 775 mm]。

目标位置在机械臂末端的左侧，根据“最优原则”，选用第1组解。

将算例中各关节变量的值输入到ADAMS中进行仿真，可得到机械臂位姿如图5所示，在机械臂末端建立的Mark点可测得末端的位姿参数，位置参数为[5 721.73 mm 775.32 mm 853.36 mm]，与式(17)给定的预期位置虽有误差但基本一致。测得的姿态参数为[90° 30° 90°]，由于本文默认采用Z-Y-X欧拉角描述刚体姿态，因此可算得其姿态矩阵为

(18)

结果也与式(17)给定的预期姿态矩阵一致，仿真验证了运动学正解与反解求解结果的正确性。

图5 机械臂最终位姿Fig.5 Adams pose simulation

5 实验验证

为了验证该运动学算法的正确性，搭建实验平台进行实验验证，实验平台如图6所示，机械臂固定在底座上，幕布上的点代表末端要到达的位置点。

在幕布上目标点中任取10个点，将目标点的数据传输到控制器中，控制机械臂到达目标位置点，可求得末端位置的实际值，与理论值进行比较，如图7所示，从图7可以得出，存在误差，但基本一致，引起误差的原因可能是机械臂的刚度问题。

6 结论

(1)以八自由度冗余农业机器人机械臂为研究对象，求解其位置运动学模型的解析解。采用D-H法得到了正运动学方程，根据农业机器人实际工况与机械臂结构特点，建立其约束条件，采用反变换法得到各关节变量的逆运动学解析表达式，根据最短路径原则，舍去不在工作范围内的解，最终共有两组解。

图6 实验平台Fig.6 Experiment platform

图7 末端位置对比Fig.7 Comparison of end position

(2)采用ADAMS软件建立了机械臂仿真模型，对其进行运动学仿真，并搭建实验平台进行实验，验证了正逆运动学算法的正确性。