一种基于模运算的小波系数调整水印算法
2019-02-15郭功勋
陈 青,郭功勋
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
随着因特网走入千家万户,数字信息的传播更加便捷、高效.我们接触的几乎所有事物都转型为数字化,如纸质媒体到数字媒体的转化,在转型的过程中无不充斥着版权制度与传播技术的互动关系.然而,由于数字媒体容易复制、传播便捷的特点,侵犯版权等行为更难以防范.为此,在向无纸化、无胶片化转型的大背景下,数字水印技术作为一种数据保护和版权认证的方法应运而生,并逐渐发展成为现今信息领域的一个研究热点[1].在水印技术中,由于小波变换多分辨率、分解特性与人类视觉系统相符合、与常用国际压缩标准兼容等特性,使得小波域的水印技术得到广受关注[2,3].
相对于空间域的水印,基于小波域的水印算法一般更具有优势.Saravanan等[4]利用db小波,将水印嵌入到载体图像的小波系数中,增加了水印的鲁棒性;A.Siddiqui等[5]将水印嵌入到图像小波变换后的的低频子带中,由于低频子带内包含了图像的大部分信息,在其嵌入会影响图像的质量.
基于小波域的数字水印虽然可以增强图像的鲁棒性,但其在缩放、旋转等攻击下效果一般,不能很好的恢复水印图像.许多学者在此基础上引入了奇异值分解(SVD)来增强水印算法的鲁棒性.文献[6,7]利用SVD稳定性,缩放不变性等特性,将其应用于图像增强的领域内,取得了不错的效果;王祖喜等[8]利用数字全息技术和奇异值分解,首先将水印进行处理后,将处理后的图像作为水印嵌入到小波的低频子带中,虽然鲁棒性得到了增强,但其不可见性受到影响;汤永利等[9]引入μ率压缩技术,结合SVD,利用量化索引调制(QIM)来实现水印的嵌入,但文献并没有抗剪切,旋转等攻击的相关实验数据,其鲁棒性值得考究;J.Kaur等[10]结合离散小波变换与SVD实现了一种改进的数字水印算法,但其应对剪切攻击时效果不好,无法提取出水印图像;任克强[11]等提出了一种融合HVS和SVD优良特性的小波域图像水印算法,将水印嵌入到图像中人类视觉系统的较重要部分,这是把小波域的水印方法与扩频通信方法进行类比,但其无抗旋转攻击的相关数据;陈青[12]等基于小波变换的多分辨特性使得水印在不同尺度与分辨层上具有不同的鲁棒性,提出了一种基于DWT-SVD的可伸缩图像渐进性水印算法,其缺点为对高强度的嵌入比较敏感,图像的质量不够好;文献[13]基于小波和奇异值分解,利用LSB方法实现了水印的嵌入.Anita等[14]利用模糊逻辑(Fuzzy logic)技术,增强了基于DWT-SVD水印的安全性;S.Ponnisathya等[15]利用混沌映射技术对水印进行预处理,然后再利用SVD将水印嵌入到小波域中;以上两种方法更多考虑的是水印图像的安全性,其图像质量和鲁棒性并没有很大提升.
近年来,在水印算法的研究上,许多学者引入了很多新的方法,并且针对某一领域内对象图像的特征,提出了有针对性的保护措施.例如薛青晨等[16]提出了一种基于奇异值分解和小波变换的,专门针对QR码图像保护的鲁棒水印算法;T.T.Takore等[17]在常规DWT-SVD水印算法的基础上,利用遗传算法,寻找最佳比例因子来平衡图像的不可见性以及鲁棒性;A.M.S.D.Mashalkar等[18]针对图学图像(MRI)的特征,以及医学图像与患者文本信息的相关性,提出了一种基于SVD的小波域水印算法;P.Chinchmalatpure等[19]针对指纹图像的特征,以及指纹图像在安全领域内的重要地位,设计了一种专门保护指纹图像的基于SVD-DWT的图像水印算法;V.Adul等[20]基于奇异值分解和DWT,提出了一种鲁棒性的视频水印算法.上述几种算法在不同程度上都提高了水印算法的鲁棒性,但由于其各自针对领域的不同,有很大的局限性,不能广泛适用于一般图像,并且这些方法并没有针对图像质量进行优化.
本文将小波和SVD相结合,设计了一种基于模运算的SVD小波系数调整算法.首先根据载体图像携带信息的不同特征,选择像素点动态范围变化较小的平滑区进行二级小波变换,将对应小波系数进行奇异值分解,并针对常规SVD对图像系数改动较大,导致图像鲁棒性不够好的问题,利用模运算减小其系数的改变幅度,实现水印的嵌入.该算法提高了图像的质量与水印的鲁棒性,并对于一般的信号处理和几何攻击有很强的鲁棒性,尤其是抗旋转攻击方面效果突出.
2 理论背景
2.1 水印预处理
为了提高我们嵌入水印的安全性,我们必须首先对水印内容进行加密和编码.首先把要嵌入大小为32(32二值水印图像“USST”转换成二进制序列W=w1w2w3…wn;将密钥转换为二进制序列K=k1k2k3…km.这里我们采用一对一循环加密算法,将水印与密钥的二进制序列进行一对一循环取模加密,得到加密后的新水印序列M=m1m2m3ml…ml,其中,l=max{m,n}
(1)
一般说来,密钥的长度越小越有利于密钥的传输和保密.所以,在本文算法中所使用的水印图像所转换成二进制序列,要求远远大于密钥的二进制序列的长度.在加密过程之后,我们还需要将新生成的水印序列 转化为二维图像数据进行存储.这样做事为了后面进行水嵌入及提取工作的顺利进行.
循环取模编码采取的是异或操作.所以,在解码时,按照式(1),直接将密钥序列与所提取出来的水印序列再次进行异或操作,就可得到加密前的水印数据.
2.2 载体图像分块
常规的图像水印算法是将水印图像嵌入到整幅图像的频域或者小波域中,这样会对图像的质量产生影响.所以为了在保证水印鲁棒性的前提上提高图像的质量,本文提出图像动态范围分块的方法.
将载体图像划分成互不重叠的n×n个块B(1),B(2),…,B(n),其中k为块的数目.计算其平均差值Di:

(2)

(3)
其中T为预设值,满足2t1≤T≤2t2,1≤t1,t2≤5.这里T越大,分得的平滑块的数量越多,复杂块的越少.
相对来说,复杂块内像素值变化较大,包含了丰富细节特征,其相关性较差,恢复原图像较困难.而平滑块内像素值变化没那么大,其相关性强,易恢复出原图像.在此基础上,本文选择只在平滑块内嵌入水印,这样既能保证图像的鲁棒性,图像的质量还能得到显著的提升.
2.3 奇异值分解(SVD)
奇异值分解是一种将非对称矩阵进行对角化的分解方法.对于任一矩阵A,可将其分解成:左奇异矩阵U、奇异矩阵S、右奇异矩阵V.其中U、V均正交,S为对角阵.
A=U×S×VT
(4)
本文算法运用奇异值分解算法,主要是因为图像的奇异值有如下性质:
1)图像的奇异值代表了图像的能量信息,因而其稳定性很好,即当图像受到一定程度的攻击时,它的奇异值不会有太大的变化.
2)图像的奇异值具有比例不变性,这对水印抵抗缩放类攻击有很大的帮助.
3)图像的奇异值具有旋转不变性,这对水印抵抗旋转类攻击有很大的帮助.
鉴于奇异值的以上特性,我们将水印信息嵌入到小波系数经奇异值分解后,得到的奇异值矩阵里,水印信息会有很好的鲁棒性.
2.4 小波系数调整算法
由于常规奇异值分解法嵌入水印主要采用加性准则,即:
S′=S+αSw
(5)
其中α为误差范围,这样将使奇异值的改动幅度较大,不利于水印的嵌入.这里提出一种基于模运算的奇异值修改方法.对应被嵌入的二值水印的值,可对原图像分块后进行小波变换所得系数的奇异值进行如下修改:
1)当嵌入的水印w值为0时:
(6)
式中,α≥4,mod(Si,α)为奇异值Si对误差范围α的模.修改后的数据对α取模运算,当0≤mod(Si,α)<3α/4时:
=mod(mod(Si,α)+mod(α/4,α)-mod(mod(Si,α),α),α)
=mod(mod(Si,α)+mod(α/4,α)-mod(Si,α),α)
=mod(mod(α/4,α),α)
=mod(α/4,α)
=α/4
则当3α/4≤mod(Si,α)<α时,将修改后的数据对α模运算:
=mod(mod(Si,α)+mod(5α/4,α)-mod(mod(Si,α),α),α)
=mod(mod(Si,α)+mod(5α/4,α)-mod(Si,α),α)
=mod(mod(5α/4,α),α)
=mod(5α/4,α)
=α/4
2)当嵌入的水印w值为1时:
(7)
式中,α≥4,mod(Si,α)为奇异值Si对误差范围α的模.若对修改后的数据对α模运算,当0≤mod(Si,α)<α/4时:
=mod(mod(Si,α)-mod(α/4,α)-mod(mod(Si,α),α),α)
=mod(mod(Si,α)-mod(α/4,α)-mod(Si,α),α)
=mod(-mod(α/4,α),α)
=mod(-α/4,α)
=3α/4
则当α/4≤mod(Si,α)<α时,将修改后的数据对α模运算:
=mod(mod(Si,α)+mod(3α/4,α)-mod(mod(Si,α),α),α)
=mod(mod(Si,α)+mod(3α/4,α)-mod(Si,α),α)
=mod(mod(3α/4,α),α)
=mod(3α/4,α)
=3α/4
由上述分析可知,当对mod(Si,α)进行区域划分,对奇异值进行相应修改后,其改变值为α/4或3α/4.很容易可以看出,相比于加性法则,这种水印嵌入的方法减小了嵌入水印对原始载体图像的扰乱,其相关性更强,更易恢复出水印图像.
3 水印的嵌入和提取
根据鲁棒水印的设计思路,结合理论背景,对水印算法进行具体的设计.该算法分为如下几个部分:水印的预处理;载体图像区域分块;水印的嵌入算法;水印的提取与检测.水印的嵌入与提取过程如图1所示.

图1 水印嵌入与提取流程Fig.1 Watermark embedding and extracting process
3.1 水印的嵌入
在本算法中,我们首先将原图像分块,选取其中细节特征较少的平滑块作为水印的嵌入区域,将图像块进行二级小波变换,选取其中频子带,将小波系数经过改进的SVD算法求取奇异值,并嵌入水印.
水印嵌入的具体方案如下:
1)水印预处理,利用式(1)对水印图像产生的二进制序列W与密钥产生的二进制序列K进行一对一循环取模加密得到加密后的序列M,再将M转化成加密后的水印图像.
2)利用式(2)(3)对载体图像进行分块处理,选出相应的平滑块进行水印的嵌入.
3)将所选区域进行二级提升小波变换,提取LH2,并将其进行奇异值分解,得到对应的奇异值.
4)在选定的水印嵌入的区域内,将奇异值进行修改以嵌入水印.修改法则如式(6)(7).
5)使用修改后的系数,进行逆SVD变化得到嵌入水印后的LH2子带,再进行二级小波逆变换得到含水印的图像.
3.2 水印的提取
水印的提取是水印嵌入的逆过程,其算法只有略微不同.具体步骤如下:
1)对含水印载体图像进行分块并进行二级整数小波分解,提取LH2子带.
2)将LH2子带的小波系数进行奇异值分解,得到奇异值.
3)利用下式提取水印:
(8)
4)利用式(1)得到加密前的原始水印图像.
4 实验结果与性能分析
实验使用MATLAB平台对上述算法进行仿真实验.实验采用标准测试图像lena(256×256)为载体图像,以32×32的“USST”二值图像为水印图像.对lena图进行二级小波分解,根据大量的实验,我们选取阈值T=5,嵌入强度α=8.本文采用峰值信噪比PSNR度量水印算法的不可见性及图像质量,用相关系数NC检测水印算法的鲁棒性.
嵌入水印后的图像在视觉上没有明显的失真,在未受攻击水印能够正确提取的情况下,含水印图像峰值信噪比数值:PSNR=47.18,一般认为PSNR≥30时图像不可见性较好,PSNR≥36时人眼已经无法发现图像受到攻击.因此,主观视觉效果和PSNR值都证实了算法实现的水印具有良好的不可见性,图像质量好.

图2 水印嵌入和提取效果图Fig.2 Results of watermarking embedding and extraction
为了验证算法的鲁棒性,对含水印的lena图像进行各种攻击测试,并同文献[12]进行对比.
1)JPEG压缩

表1 JPEG压缩攻击下的实验结果Table 1 Results under JPEG attacks
由表1数据可以看出,随着压缩比的增大,图像的质量下降,原始水印与提取出的水印的相关系数逐渐降低,但就其变化范围来讲,水印在Q=20时仍可以能较为准确的提取,故水印算法对JPEG压缩攻击具有较强的鲁棒性.
2)噪声攻击

表2 噪声攻击下的实验结果Table 2 Results under noise attacks
由表2实验结果可知,对水印系统进行噪声攻击后,仍可能较为准确地提取.水印系统对高斯噪声比较敏感,而对椒盐噪声有较强的抵抗能力.这是由于在中频嵌入水印,而中频子带对椒盐噪声不敏感,故提高了对抗椒盐噪声的鲁棒性.
3)滤波攻击
对于各种不同的滤波攻击施加的不同窗口尺寸,水印信号归一化相关系数不同,但随着尺寸的增大呈下降的趋势,但提取出的水印信号基本可以良好分辨出USST标识,对高斯低通滤波、均值滤波和中值滤波攻击均具有良好的鲁棒性,如表3所示.
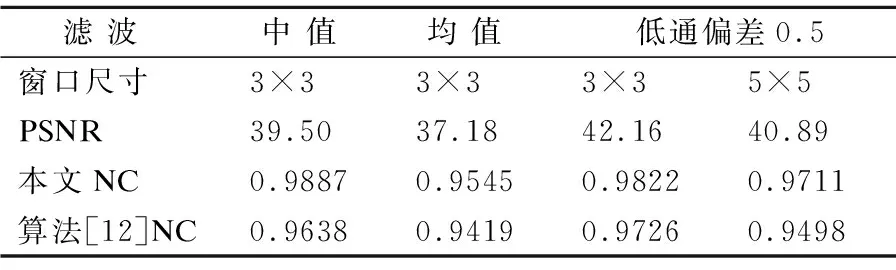
表3 滤波攻击下的实验结果Table 3 Results under filter attacks
从上面的分析可以看出,此水印算法对常规攻击具有很好的鲁棒性,并且图像的质量较好.以下就本文提出的水印方案进行几何攻击实验以验证算法的鲁棒性.
4)缩放攻击

表4 缩放攻击下的实验结果Table 4 Results under scaling attacks
因为缩放攻击存在插值运算,含水印作品在缩小攻击时丢失部分水印信息,故对缩小攻击所提取的水印信号有失真,而放大攻击没有产生原始作品信息的丢失,所以对放大攻击后仍能准确提取水印信息,如表4所示.
5)剪切攻击
对含有水印的载体图像进行剪切操作,剪切幅度分别为图像尺寸的1/8和1/4.

表5 剪切攻击下的实验结果Table 5 Results under cropping attacks
从表5实验结果可看出,本文所提出的水印算法对剪切攻击具有较强的抵抗能力.
6)旋转攻击
表6中给出了对特定角度攻击后的含水印图像和提取的水印图像,可以看出在保持图像底版不变的情况下,随着旋转角度的增加,含水印图像的边缘信息丢失的越大,水印信息与原始载体图像的同步性保持也就越差,但是对1度这样的小角度,提取的水印信号几乎没有任何失真,对10、45度这样的中等程度旋转,提取的水印信息仍具有可辨性.
由图3观察可知,对含水印作品施加小角度(0.1-1度)攻击时,提取的水印信号相关系数都在0.98以上,且在旋转0.7度后出现上升的趋势;对含水印图像施加中等角度(5-50度)的旋转攻击后,提取出的水印图像与原始水印图像有一定程度的失真,但相关系数都在0.90以上,仍然有着很高的相似度,这说明本文提出的水印算法对旋转攻击具有很好的鲁棒性.
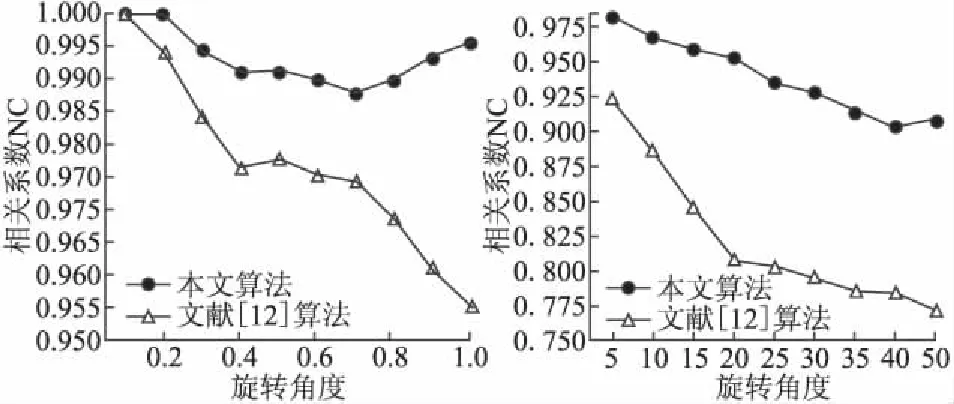
图3 旋转攻击后NC曲线Fig.3 NC curve under rotation attacks
5 结 语
本文所提出的水印方案打破在整幅图像上嵌入水印的局限,根据图像的细节特征的多少对图像进行分块,选取细节特征较少相关性较强的平滑块来嵌入水印,提高了图像的质量.本文利用奇异值分解稳定性强,有伸缩和旋转等特点嵌入水印,并针对常规算法奇异值修改较大的问题,用模运算对其进行改进,减小了嵌入水印对原始载体图像的扰乱,提高了水印算法的鲁棒性.实验结果显示,图像的质量较好,水印算法能保持较强的鲁棒性,并综合平衡了水印的各项主要指标,具有一定的实用价值.
