复杂内核数据结构的形式化描述和验证
2019-02-15冯新宇
马 顶,付 明,乔 磊,冯新宇
1(中国科学技术大学 计算机科学与技术学院,合肥 230027) 2(华为上海研究所 2012实验室-OS内核实验室,上海 201206) 3(北京控制工程研究所,北京 100190) 4(南京大学 计算机软件新技术国家重点实验室, 南京210023)
1 引 言
复杂数据结构是相对于规则数据结构而言的.规则数据结构是指数组、单链表、双链表、二叉树等可以归纳定义的数据结构.规则数据结构可以使用基于归纳谓词的分离逻辑断言来描述,已经有大量的研究工作[1-5]关注这类数据结构的自动化和半自动化验证技术.而复杂数据结构是指将多种规则数据结构组合在一起来管理组织数据的数据结构.内核设计者为了优化程序的时空间效率通常会采用复杂数据结构来管理内核数据.内核中复杂数据结构一般有由多种结构组成和多个结构间高度耦合的特点.
国外已有的操作系统内核验证项目,譬如seL4[6,7]、 CertiKOS[8,9],它们验证的目标内核都是为了验证而新开发的,内核API的算法和所使用的数据结构都是自己设计的,为了让验证变得相对比较容易,在内核数据结构的选择和设计上会尽可能的避免使用复杂内核数据结构.复杂内核数据结构的形式化描述和验证在上述这些操作系统内核验证项目中没有得到充分的研究.
Gerwin Klein等人使用定理证明工具Isabelle/HOL[注]http://isabelle.in.tum.de/overview.html对seL4中的关键数据结构进行定义和验证[注]http://sel4.systems/Info/Docs/seL4-spec.pdf.seL4中主要的数据结构如进程管理结构是通过双向链表来实现的,他们在形式化描述双向链表时用有序的列表结构来模拟双向链表结构,并不描述双向链表中相邻节点间的前后指向关系,双向链表中节点的顺序用在列表中的次序来体现.这种描述方式定义的断言中包含的信息太少了,很难用来验证复杂的代码.
Ronghui Gu等人使用定理证明工具Coq[注]https://coq.inria.fr/中对CertiKOS中的数据结构进行形式化定义,CertiKOS中的关键数据结构主要是双向链表结构.CertiKOS中定义了一个长度为64的tcb结构体数组用于存储进程控制块的信息,一个长度为64的双向链表表头结构体数组用于存储内核中各个双向链表的表头结构体.在对双向链表形式化定义时,他们使用Coq中的Inductive关键词对双向链表结构进行归纳描述,并不描述一个链表和别的链表的组合关系.如果双向链表结构中节点的内容较简单,没有其它的指向关系,这种方式可以适用,然而当双向链表结构同时和别的结构相关联时,这种定义方式难以适用.国内外也有很多针对不同数据结构形状的程序验证工作[10-13],这些工作主要是考虑对规则形状的数据结构的自动化验证,并不考虑复杂数据结构的验证技术,复杂数据结构由于多种形状耦合在一起,数据约束关系复杂,自动化验证很难做到.
对内核中用到的数据结构进行形式化描述是内核验证的关键工作之一,并且好的结构断言对提高后续的代码验证工作的效率也有很大的帮助.传统的描述规则数据结构方法有两个缺点,一是难以刻画复杂数据结构的组合关系,二是会导致相关的代码验证工作复杂化.针对内核中复杂数据结构的特点,本文提出用拆分法来形式化定义复杂内核数据结构,并且提出将规则结构断言的形状和内存块分开描述来避免代码验证中对结构断言的展开过程,以简化相关的代码验证工作.本文的主要贡献有以下几点:
1)提出用结构拆分法定义复杂内核数据结构.
2)提出在描述组成复杂数据结构的基本数据结构时将形状和内存块部分分开定义.
3)形式化定义了某航天操作系统内核的进程管理数据结构.
4)验证了该内核中的任务创建模块和任务调度模块.
2 复杂内核数据结构
复杂内核数据结构一般是由多个结构复合而成的数据结构,本章通过几个例子说明复合数据结构的特点,以及传统断言定义方式在描述复合数据结构时的不足之处.
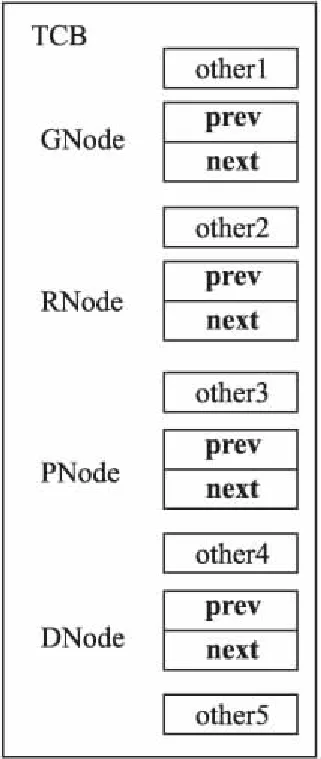
图1 TCB结构体Fig.1 TCB structure
2.1 复合数据结构
图1所示为内核中进程管理数据结构的TCB结构体.TCB结构体都嵌入了4个Qnode类型的结构体,分别为GNode、RNode、PNode和DNode.其中other1、other2、other3、other4和other5为TCB中其它的域.prev、next双向链表节点的前驱和后继指针.
图2为该航天操作系统内核的进程管理数据结构的结构图.如图2所示,内核中有4类双向链表,分别为全局链表、就绪链表、阻塞链表和延时链表.其中全局链表内核中只有一个,用来组织内核中所有的TCB(Task Control Block),当需要访问某进程的TCB时,需要通过全局链表来获取该进程的TCB信息.其中所有进程TCB的GNode组成内核中唯一的全局链表;就绪进程TCB的RNode按照任务优先级在内核中组合成多个就绪链表;阻塞进程TCB的PNode按照任务等待的资源不同组成多个阻塞链表;延时进程TCB的DNode组成内核中唯一的延时链表.

图2 进程管理树结构图Fig.2 Data structure of process management
结构断言要描述的信息包含两部分:一是内存块的值 信息,二是内存块间的指向关系.该内核的进程管理结构上同时含有多个链表,链表节点耦合在一个大结构体中,不同的链表间的节点顺序也不一致,指向关系复杂,导致该结构非常难以刻画.
Linux 内核中哈希表采用拉链法解决哈希冲突,将所有关键字为同义词的节点链接在同一链表中.其结构由指针数组和双向链表结构组合而成.在定义该结构时需要刻画数组元素的值和链表首地址之间的关系,传统定义方式难以实现.其结构图如图3所示.

图3 Linux哈希表Fig.3 Linux Hash table
利用数组存储链表节点的向导指针可以实现链表节点的随机访问.图4中双向链表的每一个节点在数组中都存有一个指向该节点的指针,通过数组的下标可以随机访问链表中的节点,其中链表的奇数节点指针保存在A[] 数组中,偶数节点保存在 B[] 数组中.通过数组的下标可以避免在访问节点过程中对链表结构的遍历过程,实现对链表奇数、偶数节点的快速访问.用传统定义方式刻画随机访问链表,相关代码的验证会变得很复杂,十分难以验证.
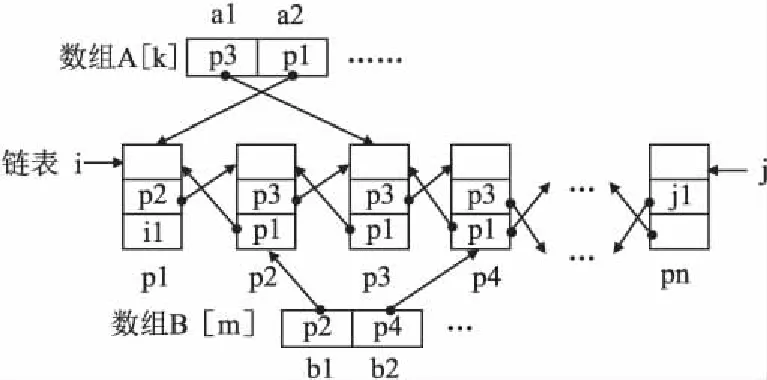
图4 随机访问链表Fig.4 Random access linked list
内核当中经常会设计一些如上文提到的内核的进程管理数据结构、Linux 内核哈希表以及随机访问链表这样的复合数据结构来管理和组织数据.而复合数据结构的复合关系有时会非常复杂,导致数据结构难以形式化定义和验证.
2.2 传统结构断言定义方式的不足
对单链表、双链表、二叉树等规则数据结构而言,都可以用传统的结构断言方式来刻画.传统的结构断言定义方式有以下几个特点:
1)断言递归定义.
2)节点首地址隐藏在断言内.
3)形状和内存块放在一起定义.
图5中i为单链表的头指针,next为节点的后继指针,链表最后一个节点的后继指针为空指针.

图5 单链表Fig.5 Structure of single linked list
传统方式中单链表断言的定义为:


单链表片段sllseg的定义中i为指向首节点的指针值,j为链表最后一个节点后继指针的值,α为链表节点的内存内容.sllseg在描述节点的内存信息时,用存在量词构造节点后继指针的信息,进而递归定义后续的链表片段.
在单链表片段sllseg的定义中,链表节点首地址信息是在sllseg内部是用存在量词构造出来的,而当描述多个结构之间的关系时,必然需要知道不同结构中内存块首地址的信息,这样的定义显然不满足要求.sllseg在描述链表节点内存信息的同时也描述了链表结构中相邻节点的指向关系,体现了形状和内存同时刻画的特点.
然而,复杂内核数据结构通常是多结构耦合的组合数据结构,不同结构间存在复杂的组合关系,这样的数据结构不存在一个归纳结构使得可以递归定义相应的结构断言;而且,由于节点首地址信息隐藏在断言内部,导致结构间组合关系难以刻画;形状和内存块放在一起定义使得在验证相关代码时需要对结构断言进行拆分,导致验证过程复杂化.
3 形式化定义
3.1 分离逻辑断言语言
操作系统内核代码通常使用C语言实现,会大量使用 指针实现对内核数据结构的访问.分离逻辑是对Hoare[14]逻辑的扩展,支持对指针程序的模块化推理.本文使用分离逻辑断言语言来刻画内核数据结构,下面首先给出分离逻辑断言的定义及其语义.

(Store) s∈Id→Addr
(Heap) h∈Addr→Val×Type





断言是对程序状态的刻画,程序状态用符号表Store和内存Heap二元组来描述.其中Store是变量到地址的映射,Heap是地址到内存值及类型二元组的映射.其中(s,h)emp表示内存为空;(s,h)[P]表示当前状态满足(s,h)emp且性质P成立;(s,h)a(v,τ)表示地址为a的内存单元中保存了τ类型的内存值v;(s,h)x(v,τ),表示全局变量x的类型为τ,且在内存中保存了τ类型的值v;(s,h)∃x.p表示在当前状态下,存在x满足命题p;(s,h)p*q表示在当前状态下,可以将内存分成不相交的两部分h1、h2,断言p在h1上成立,断言q在h2上成立.
(Type) τ::=Tnull|Tvoid|Tint8|Tint16|Tint32|Tptr(τ)|Tcomptr(id)|Tarray(τ,k)|Tstruct(id,D)
(DeclList) D::=nil|(id,r)::D′(ValueList)vl::=nil|v::vl′
(BlockListValue) svll::=nil|(a,vl)::svll′
(ValueList) vl::=nil|v::vl′
(Addr) a∈Block×off Block∈Z off∈Z
(Value) v::=Vundef|Vnull|Vint(n)|Vptr(a)


接着给出变量类型、表达式值、内存地址的定义.其中τ表示变量类型;|τ|表示相应类型的字节长度;szstruct(D)表示结构体类型的字节大小;DeclList 是由变量和变量类型二元组构成的声明列表;Value表示表达式或者变量的值;ValueList是值表,用来刻画数组、结构体类型变量的内存值;BlockListValue是内存块列表的值,内存块列表中的每个内存块除了给出值表外还给出首地址的信息.
然后给出结构体断言的定义,结构体断言定义如下:


∧τ≠Tstruct(-D1)∧D=(id,τ)::D′
if vl=vl1++vl′∧D=(id,t)::D′
∧τ=Tstruct(-,D1)∧|vl1|=|D1|
if vl1=vl1++vl′∧D=(id,τ)::D′
∧τ=Tarray(τ′,n)∧|vl1|=n
if vl=nil∧D=nil
otherwize
结构体断言Astruct的定义有3个参数:结构体首地址(b,o),类型τ,值表vl.其中τ=Tstruct(id,D)要求τ为结构体类型,id为结构体标识符,D为结构体声明列表.Astruct′按照声明列表D的顺序依次描述结构体各个字段的内存信息.当某个字段的类型也为结构体类型时,Astruct′的定义跳过对该字段的描述.这么定义是为接下来从内存上拆分结构做准备.另外当字段类型为数组类型时,其内存通过定义Aarray来描述.Astruct′中符号"++"表示列表连接符,|vl1|是值表的长度,|D1|是结构体声明列表的长度.
数组断言Aarray的定义如下:

数组断言Aarray的定义有3个参数:数组首地址(b,o),类型τ,数组值表vl.τ=Tarray(τ′,n)要求类型τ为数组类型,τ′是数组的元素类型,n是数组的长度.Aarray′按照数组的长度依次归纳描述数组各个元素的内存,当数组元素类型为结构体类型时,元素内存用Astruct描述.
3.2 双向链表的形式化定义
本文给出双向链表的形式化定义.图6为双向链表的结构图,图中prev、next的为链表节点的前驱和后继指针,i为指向链表首节点的指针,j为指向链表尾节点的指针,null为空指针.

图6 双链表结构图Fig.6 Structure of double linked list
形式化定义双向链表结构断言有两种方式,一种是在断言中同时描述节点内存和节点间的指向关系,另一种是分开描述内存和指向关系.下文中称描述指向关系的部分为形状.下面首先给出形状和内存同时描述的定义.

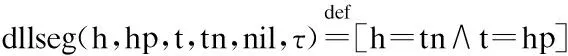

上面的定义中,dll有4个参数:h为指向链表头节点的指针的值,t为指向链表尾节点的指针的值,svll∈BlockListValue,τ表示链表节点的类型.BlockListValue的定义为:
(BlockListValue) svll∷=nil|(a,vl)∷svll′
其中,a为内存块的首地址,vl为内存块中存的值.
链表片段dllseg的参数中除了hp和tn之外,其它参数的含义与dll相同.hp为链表片段首节点的前驱指针的值,tn为链表片段尾节点的后继指针的值.dllseg对svll进行归纳定义,当svll为nil时,要求h=tn并且t=hp;当svll=((a,vl)::svll′)时,先用Astruct描述第一个节点的内存,然后再递归定义后续的内存.
另外,vl.prev=hp和vl.next=h′分别刻画了当前节点与前一节点及后一节点的指向关系.h′虽然也是用存在量词构造的,但是可以却可以通过关系h= a,在后续的归纳过程中将后续节点的首地址信息通过参数svll传递出去,从而避免传统定义方式中首地址被隐藏的缺点.
dllseg的定义中vl.prev和vl.next分别表示节点前驱指针的值和后继指针的值.dllseg同时描述形状和内存.这种定义方式在某些情况下会导致代码验证起来很困难.下面以swap函数为例,说明这种情况.
图7为swap的C代码,其中函数有三个参数Pi,Pj,和H.Pi、Pj为指向双向链表中任意的两个不相邻节点的指针,H为Head类型的指针,Head有head和tail两个域,分别为指向双向链表首尾节点的指针.

图7 swap函数C代码Fig.7 Code of swap function in C
swap的功能是交换链表中Pi和Pj指向的节点.代码(图7)的第2-5行先保存Pi和Pj的前驱、后继指针的值,第6-9行把Pi和Pj前驱、后继指针的值相互交换,第10-25行将Pi在原链表中的前驱节点的后继指针与后继节点的前驱指针改为指向Pj,对Pj也做对称处理.最后根据Pi和Pj是否为首尾节点对链表的首尾指针做相应的修改.因为代码操作的是链表中两个不相邻的节点,所以swap函数的代码实现中不包含 Pi与Pj相邻的执行路径.
swap函数的前断言定义为:


dll(h,t,svll,Qnode)*
[pi∈get-addrs(svll)∧pj∈get-addrs(svll)]*
[svll[pi].prev≠pj∧svll[pi].next≠pj]
前段言中pi、pj和ph分别是指针变量Pi、Pj、H的值,h、t是H指向的表头结构体中存储的首尾指针的值.svll中保存了链表节点的信息,get-addrs(svll)为链表节点首地址的集合(下文会给出get-addrs的定义),svll[pi].prev和svll[pi].next分别代表Pi节点前驱和后继指针的值.

图8 拆分双向链表Fig.8 Destruct double linked list
在证明过程中,当走到代码(图7)的第6行和第7行时,要对双向链表结构断言进行拆分.原因是代码修改了Pi节点的前驱后继指针,导致此时的内存不满足链表形状性质的要求.拆分结果如图8所示.Pi为拆分出的节点,L1为链表在Pi前面的片段,L2为Pi后面的片段.
拆分前双向链表断言为:dll(h,t,svll,Qnode),拆分后断言变为:
dllseg(h,Vnull,t1,pi,svll1,Qnode)*
Astruct(pi,Qnode,vl)*
dllseg(h1,pi,t,Vnull,svll2,Qnode)*
[vl.prev = t1∧vl.next = h1∧svll = svll1++(pi,vl)::svll2]*
[pj∈get-addrs(svll1) ∨ pj∈get-addrs(svll2)].
其中"++"表示列表连接符,vl为Pi节点的值表,svll1为L1片段的内存块列表,svll2为L2片段的内存块列表.
接下来走代码(图7)的第8行时,需要访问Pj节点,然而Pi和Pj是链表中任意的两个节点,因此不知道Pi和Pj在链表中的先后关系,也就不知道Pj属于L1还是L2,对此要分情况讨论.然而,当在代码中同时访问多个节点时,就需要进行大量的讨论,这会导致代码验证起来非常困难.而当将链表断言的内存和形状分开描述时,就可以避免这种讨论,从而简化验证难度.
下面给出内存和形状分开描述的双向链表断言的定义.


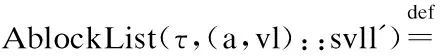


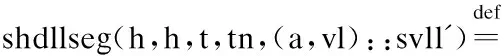
链表断言Adll中的参数和上文中dll参数的含义一样.如上式所示,Adll由AblockList和shdll两部分组成,AblockList与shdll有相同的参数svll.其中AblockList对svll做归纳,逐个描述链表中所有节点的内存信息,而shdll同样对svll做归纳,但只是描述相邻节点的指向关系,而不描述内存信息.
以图9为例,a、b为内存块首地址.AblockList只提供信息说节点a中存了3个值100、p1和p2,b中存了101、p4和p3,但是却没说p1与b以及p3与a之间的关系;而shdll则不管a、b中到底存了什么信息,只说a中的p1就是b,b中的p3就是a.
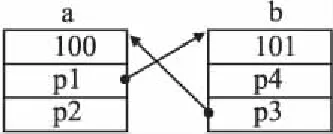
图9 例子Fig.1 Example
与前种方式定义的链表断言相比,当参数一致时,两种定义方式描述的内存信息是一样多的,且都描述了相邻节点的指向关系,因此两种定义方式提供了同样多的信息,是等价的.
使用后一种方式定义的链表断言来证明swap时,可以避免前一种定义方式需要分情况讨论的问题.在走swap第6行前链表断言为Adll(h,t,svll,τ),第6行代码(图7)修改pi节点的前驱,链表断言变为:

从上述分析可以看到,当将内存和形状分开描述之后,对节点内存的修改可以只体现在AblockList的变化上,而形状部分则可以暂时保留旧的信息.从而避免了验证过程中的断言拆分,也就避免了分情况讨论的问题.
总结形状和内存分离的好处,有以下两点.
1) 延迟维护内存与形状的一致性:
在链表断言中同时刻画内存和形状导致需要断言拆分的根本原因在于需要时时保证内存和形状的一致性.而以分离形式定义的链表断言中,shdll只是描述纯的形状性质,由此允许在内存信息发生变化时,shdll可以仍然维持旧的信息,不用立即与内存保持一致.从而达到避免分情况讨论的目的.
关于何时维护内存和形状的一致性的问题,因为在使用推理规则验证程序的过程中,每次向前推理一条语句,都要检查语句执行的前条件,而语句的前条件是在推理规则中已经写好的.譬如验证swap函数,采用向前推理的话,假设在走完swap函数的第25行之后描述程序状态的断言变成A,接下来验证return语句时,用于推理return语句的推理规则会要求A能够蕴含出函数后条件.而函数后条件会要求此时的内存中存在一个双向链表结构,这时为了验证程序满足函数规范就需要维护内存和形状的一致性.
延迟维护形状和内存的一致性是否会导致验证漏洞?答案是不会.因为延时维护形状和内存的一致性,只是在内存发生变化时不立即对内存进行形状性质的检查,但是内存上发生的变化是会被记录下来的,而内存上具体发生什么变化依赖于函数的具体实现.如果程序形状操作有误,那么在该操作执行之后得到的内存断言上不会凭空出现足够的信息使得其可以通过形状检查.以swap函数为例,swap函数的后条件会要求,最终内存上存在一个双向链表,并且该双向链表相对于前条件的链表结构交换了指定的节点在链表中的次序.如果形状操作有误,那么在最后推理return语句时,内存上不会存在一个满足函数后条件的双向链表结构.假如说在形状操作有误的情况下,还能验证出程序满足函数规范,理由只可能有一个,就是函数后条件写得太弱了,譬如说在定义函数规范时将后条件写成true,那么无论如何在推理return语句时都能通过.所以,只要保证函数规范是正确的,那么不会因为延迟形状和内存的一致性使得内存能够通过形状检查,得出一个不正确的程序满足函数规范的结论.
2)允许随机访问链表节点:
在复合数据结构中是允许编写随机访问链表节点的代码的,例如与随机访问链表结构(图4)相关的代码.当同时访问链表中的多个节点时,在验证中需要进行大量的讨论,并且情况随着节点数目的增多快速变得复杂,导致相关的代码非常难以验证.而采用形状和内存分离的形式描述结构断言,则可以大大缓解这一情况.
由此,本文提出采用形状和内存分离的形式刻画组成复杂数据结构的基本数据结构.
3.3 定义复杂数据结构
本文提出使用结构拆分法定义复杂数据结构.拆分法包含两方面:
1)结构拆分,将复杂数据结构按照其内部组成拆分成若干子结构,分别进行定义.
2)定义子结构间的组合关系,将各子结构通过组合关系联系起来.
内核中的数据结构将计算机中分离的内存通过指针组织在一起存储数据.形式化定义数据结构要描述的内容包括两部分:一是节点的内容,即节点的内存信息;二是节点间由指针建立的指向关系.因此,无论使用什么样的方法,只要在结构断言中完整地描述结构中的节点的内存和结构间的组合关系就可以正确地描述被使用的数据结构.
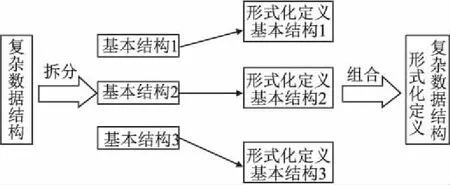
图10 结构拆分过程Fig.10 Process to decompose the structure
如图10所示,通过对复合数据结构进行拆分,可以将结构断言分成两层:一是组成复杂数据结构的各个基本数据结构的断言,二是各子结构之间的组合关系.
下面以某航天操作系统内核的进程管理结构为例,说明定义复杂数据结构的过程.
3.3.1 结构拆分
首先对内核的进程管理结构进行拆分,然后对拆分出的子结构进行形式化定义.
进程管理结构中结构体TCB的C代码定义如下所示:
struct TCB {
…
struct Qnode GNode;
…
struct Qnode RNode;
…
struct Qnode PNode;
…
struct Qnode DNode;
…
}
TCB结构体嵌入了4个Qnode结构体,GNode、RNode、PNode和DNode.在内核中分别组成全局链表、就绪链表、阻塞链表和延时链表.
对应图2,可以将进程管理结构拆分成8个部分:
1)空心进程控制块(图11);
2)所有进程的GNode集合(图12);
3)延时进程的DNode 集合(图13);
4)非延时进程的DNode集合(图13);
5)就绪进程的RNode集合(图15);
6)非就绪进程的RNode集合(图15);
7)阻塞进程的PNode集合(图14);
8)非阻塞进程的PNode集合(图14).
将TCB的GNode、RNode、PNode和DNode的内存挖去,可得到有4个空心的TCB.

图11 空心进程控制块Fig.11 Cavities TCB
图11中虚线框住的部分代表被挖去的内存,other1、othter2、other3、other4和other5为TCB的其它部分,TCBi(i∈{1,2,3,4,5})为相应TCB内存块的首地址.用上文定义的不描述嵌套结构体内存的Astruct来描述单个空心TCB的内存:

其中TCBi为进程控制块的首地址,TCB为类型,tcbvl为相应节点中存储的值.因为Astruct在定义的时候会跳过类型为结构体的字段,所以ATCB(tcbvl)中不描述TCB中嵌套的子结构体的内存,从而将Qnode从TCB挖出.被挖出的Qnode结构体的内存将在其它部分进行描述,从而实现结构拆分.所有空心TCB的内存可以用AblockList(在第3.2 节定义)来描述,则空心TCB集合可以定义为:
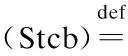
其中Stcb∈BlockListValue,TCB表示结构体类型.
GNode的内存在Global链表描述,Global链表定义为:

上述定义中,Adll为描述双向链表的断言,hg和tg分别为指向Global链表首尾节点的指针的值,svllg包含全局链表中内存块首地址和值的信息,Qnode为描述链表中内存块的值所需的类型信息.
以图12为例,图中Gi(i∈{1,2,…,5})表示内存块的首地址,GHead和GTail分别为链表的首尾指针.svllg包含了内存块Gi(i∈{1,2,…,5})的首地址和内存值信息,hg、tg则分别为GHead和 GTail的值.
对DNode而言,要将DNode按照所属的进程是否是延

图12 全局链表Fig.12 Global double linked list
时态进程,分成属于Dealy链表和不属于Delay链表两部分.链表部分的内存用双向链表断言Adll描述,非链表部分的内存用AblockList描述,则有:

其中链表部分的内存信息在断言Adelay(hd,td,svlld)中描述,非链表部分的内存在ANdelay(Sdelay)中描述.

图13 Delay节点集合Fig.13 Delay node set
以图13为例,Adelay断言描述了D1、D3和D4的内存信息,以及彼此之间的指向关系;ANdelay断言描述了D2和D5的内存信息.

图14 阻塞节点集合Fig.14 Pend node set
对于RNode和PNode,同样地可以按照进程的状态将RNode和PNode分成链表部分和非链表部分,如图14和图15所示.其中链表部分用断言Adll描述,非链表部分用AblockList描述.
3.3.2 组合关系
单纯地描述复合结构的各个子结构是不够的,还要将它们组合起来才可以正确地描述复合数据结构.通过刻画各个子结构间的组合关系,将各个子结构组合在一起.
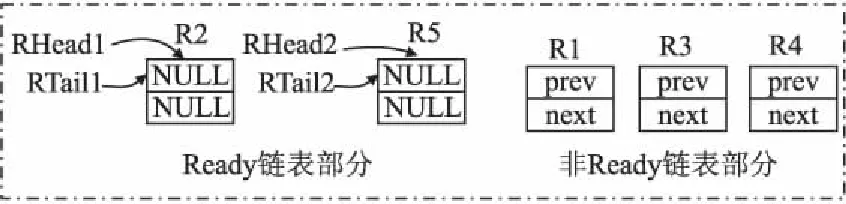
图15 就绪节点集合Fig.15 Ready node set
下面以GNode、DNode与空心TCB间的组合关系为例,说明组合关系的定义过程.
要正确地描述进程管理结构,需要保证:
1) 结构中所有链表中的节点指向关系都得到了描述.根据上文的定义,该航天操作系统内核中所有的链表都已经用双向链表断言描述了.
2) 保证内存信息都得到正确地描述.
为了保证这两点,需要刻画各结构间的组合关系.
而是否在内存上正确地定义了进程管理结构,要看拆分前和拆分后的断言描述的内存信息是否一样多.为了保证拆分前和拆分后的内存信息是一样多的,需要保证:
1)从TCB内存块中挖出的内存都得到了描述:这样保证了拆分法描述的断言中的内存信息,不少于拆分前完整TCB的内存信息.
2)子结构断言中描述的任意GNode、DNode、RNode和PNode内存块,都可以找到对应的空心TCB内存块,即所有的Qnode内存块都可以还回去:这样保证了所有被描述的Qnode内存,都是从TCB中挖出来的,从而保证拆分后的内存信息不多于拆分前完整TCB的内存信息.
从而能保证从内存上正确地定义了进程管理数据结构.
提取每个GNode内存块的首地址,则可以得到一个关于GNode的首地址集合.以图12为例,则可得到首地址集合{Gi|i∈{1,2,…,5}},下文简记为{Gi}.同样地可以得到关于空心TCB的首地址集合{TCBi}.将GNode和DNode在结构体TCB中的地址偏移分别记为offg和offd.要保证GNode满足1)、2)两点,只要保证:
1)对集合{Gi}中任意的一个地址Gi,都有Gi-offg∈{TCBi}:这可以保证GloalNode内存块都是从TCB内存块中挖出来的,保证了条件2).
2)对集合{TCBi}中的任意一个元素TCBi,都有TCBi+offg∈{Gi}:这样便保证了从任意一个TCB中挖出的GNode的内存都得到了描述,从而满足条件1).
要让i、ii同时成立,只需要:{Gi-offg|i∈{1,2,…,5}}={TCBi}成立.
同理只要{Di-offd}={TCBi},便可使DNode也满足1)、2)两点.
上文中分别用断言Aglobal(svllg)和ATCBSet(Stcb)来描述GNode和空心TCB的内存.其中参数svllg、Stcb都属于BlockListValue.BlockListValue是地址、值表二元组的列表,所以svllg和Stcb中包含了各自首地址的信息.因此可以构造函数get-addrs和get-addrs1,从svllg和Stcb中提取地址信息.
以图12为例,get-addrs1(svllg,offg)构造了集合{Gi-offg|i∈{1,2,…,5}}.同样地get-addrs(Stcb)则构造了集合{TCBi},因此GNode和空心TCB间的组合关系可用
get-addrs1(svllg,offg)=get-addrs(Stcb)
来描述.
对DNode与空心TCB之间的关系可以描述成:
get-addrs1(svlld,offd) ∪ get-addrs1(Sdelay,offd)={TCBi}
其中svlld、Sdelay∈BlockListValue,分别为包含延时链表部分和非延时链表部分的内存块信息.
要使RNode和PNode也满足1)、2),同样地也要构造集合{Ri-offr}和{Pi-offp},使之与{TCBi}相等.可以用与处理GNode与DNode时一样的方法描述{Ri-offr}和{Pi-offp}与{TCBi}的关系.
通过组合关系可以保证拆分法定义的断言正确地描述了完整TCB的内存信息.
4 验 证
作者在某航天操作系统内核的进程管理结构定义的基础之上成功验证了该内核的任务创建和任务调度模块的代码.其中任务创建模块涉及了对就绪链表的插入操作,任务调度模块

表1 统计结果Table 1 Statistical result
涉及对就绪链表的遍历操作.实现任务创建模块的C代码共计大约70行,任务调度模块中调用了上下文切换函数,实现上下文切换和任务调度的C代码共计约60行.所有的代码证明都是在定理证明工具Coq中进行的,其中用于验证任务创建模块的Coq脚本共计约5300行,用于验证任务调度模块的Coq脚本共计约1660行.统计结果见表 1.
5 结 论
一直以来,内核验证领域为简化问题,都尽量避免复杂的数据结构.而商用内核则经常会采用一些复杂的数据结构.对于复杂内核数据结构的形式化定义和验证没有经验可循,由此本文根据以往在工作中对内核复杂数据结构的认识提出利用结构拆分法来形式化定义内核中使用的复合数据结构,并且在刻画基本数据结构时采用形状和内存分别定义的形式来描述.
通过结构拆分将定义复杂数据结构的问题转化为定义多个基本数据结构及它们之间的组合关系的问题,达到问题分解的目的.将刻画基本数据结构的断言分成形状和内存两部分进行描述,可以有效地简化与基本数据结构相关的代码验证.
利用本文提出的方法,笔者成功刻画了某航天操作系统内核的进程管理结构,并且成功验证了该内核内核的任务创建和任务调度模块.实践证明,本文提出的方法是可行且有效的.
