奥克托今/3-硝基-1，2，4-三唑-5-酮共晶炸药晶体缺陷的分子动力学研究

2019-02-15杭贵云余文力王涛王金涛苗爽

兵工学报 2019年1期

杭贵云，余文力，王涛，王金涛，苗爽

(火箭军工程大学核工程学院, 陕西西安 710025)

0 引言

奥克托今(HMX)是一种常见的高能炸药，也是目前综合性能最好的单质炸药之一，因此长期以来备受关注。但HMX的机械感度较高，从而导致其发展应用受到限制。3-硝基-1,2,4-三唑-5-酮(NTO)是一种高能钝感炸药，能量接近于黑索今(RDX)，感度与1,3,5-三氨基-2,4,6-三硝基苯(TATB)相当。近年来，共晶成为一种改善含能材料性能的有效途径，并在含能材料领域得到发展应用[1-4]。2013年，Lin等[5]研究了HMX/NTO共晶炸药的性能，结果表明，HMX/NTO共晶炸药的感度低于HMX，安全性较好，且共晶具有较高的能量密度。因此，HMX/NTO共晶炸药有望成为一种新型高能炸药。

HMX通常采用改进型乙酸酐法制备，在产物中会存在杂质成分RDX. 在HMX/NTO共晶炸药制备过程中，RDX也会进入到共晶炸药中，从而导致制备的炸药不纯，即存在掺杂缺陷。此外，在晶体的生长过程中，由于外界因素的干扰，晶体的生长过程可能会受到影响，从而使晶体中存在缺陷。晶体缺陷的存在会影响炸药的性能，如稳定性、感度、能量特性与力学性能等，从而进一步影响武器弹药的威力与安全性[6-10]。因此，研究晶体缺陷对炸药性能的影响，具有一定的军事意义与实际应用价值。

本文分别建立了“完美”型与含有晶体缺陷(掺杂、空位与位错)的HMX/NTO共晶炸药模型。在材料计算软件Materials Studio 7.0(以下简称MS软件)中，采用分子动力学方法，预测了各种模型的稳定性、感度、爆轰性能与力学性能并进行了比较。研究成果可以为炸药的性能评估提供相关的理论指导。

1 计算模型与计算方法

1.1 单个分子的建立

HMX/NTO共晶炸药由HMX与NTO组成，摩尔比为1∶1. 在MS软件中，分别建立HMX与NTO的分子模型，如图1所示。

1.2 HMX/NTO共晶初始模型的建立

本文中使用的HMX/NTO共晶炸药初始结构为模拟结构。HMX/NTO共晶炸药属于三斜晶系，空间群为Pī，晶格参数a=0.906 0 nm，b=0.819 0 nm，c=1.027 0 nm，α=81.94°，β=98.42°，γ=82.03°，单个晶胞中包含2个HMX分子与2个NTO分子[5]。HMX/NTO共晶炸药的单个晶胞模型如图2(a)所示，而后将单个晶胞模型扩展为36(4×3×3)的超晶胞模型，其中包含72个HMX分子与72个NTO分子，一共144个分子，如图2(b)所示。为了便于与含有晶体缺陷的模型进行比较，将“完美”型晶体模型记作模型1.

1.3 HMX/NTO共晶缺陷模型的建立

用4个RDX分子替换“完美”型晶体中的4个HMX分子(图3(a)中标记为黄色)，得到掺杂率为2.78%的缺陷晶体模型，如图3(b)所示，将所得缺陷模型标记为模型2.

类似地，分别用6个RDX分子替换初始模型中的6个HMX分子，用8个RDX分子替换8个HMX分子，得到掺杂率分别为4.17%、5.56%的缺陷晶体模型，分别标记为模型3、模型4.

删除超晶胞模型中的4个HMX分子(图4(a)中标记为黄色)，得到空位率为2.78%的缺陷晶体模型，如图4(b)所示，将缺陷晶体模型标记为模型5.

采用同样的方法，分别删除初始模型中的4个NTO分子、2个HMX与2个NTO分子、8个HMX分子、8个NTO分子、4个HMX与4个NTO分子，将所得空位缺陷的模型分别标记为模型6～模型10.

将初始模型中最上层的HMX分子(图5(a)中标记为黄色)向上方移动0.2 nm的距离，得到含位错缺陷的晶体模型，如图5(b)所示，将缺陷晶体模型标记为模型11.

类似地，将初始模型中最上层的HMX分子向下方移动0.2 nm的距离，得到位错缺陷晶体模型，标记为模型12.

1.4 计算条件设置

分别对HMX/NTO共晶炸药的“完美”型与含有晶体缺陷的模型进行能量最小化，对其结构进行优化，而后进行分子动力学计算，其中温度设置为295 K，压力设置为0.000 1 GPa，选择恒温恒压(NPT)系综与COMPASS力场[11-12]。之所以选择COMPASS力场进行分子动力学模拟，是因为该力场适用于凝聚相和不同类型物质相互作用的研究，能在较大范围内对处于孤立体系和凝聚态体系的多种物质的性能进行准确预测。采用Andersen控温方法[13]与Parrinello控压方法[14]，范德华力(vdW)的计算采用atom-based方法，静电作用的计算采用Ewald方法，时间步长为1 fs，总模拟步数为2×105步，其中前105步用于热力学平衡计算，后105步用于统计分析。模拟过程中，每103fs保存一次轨迹，共得100帧轨迹文件。

2 结果分析

2.1 HMX/NTO共晶的晶胞参数

表1给出了“完美”型的HMX/NTO共晶模型在295 K下NPT模拟所得晶胞参数和密度。为方便比较，表1中还给出了理论计算结果。从表1可以看出，计算得到的HMX/NTO晶胞参数、密度与理论值非常接近，吻合较好，表明COMPASS力场对HMX/NTO晶体具有较好的适用性。

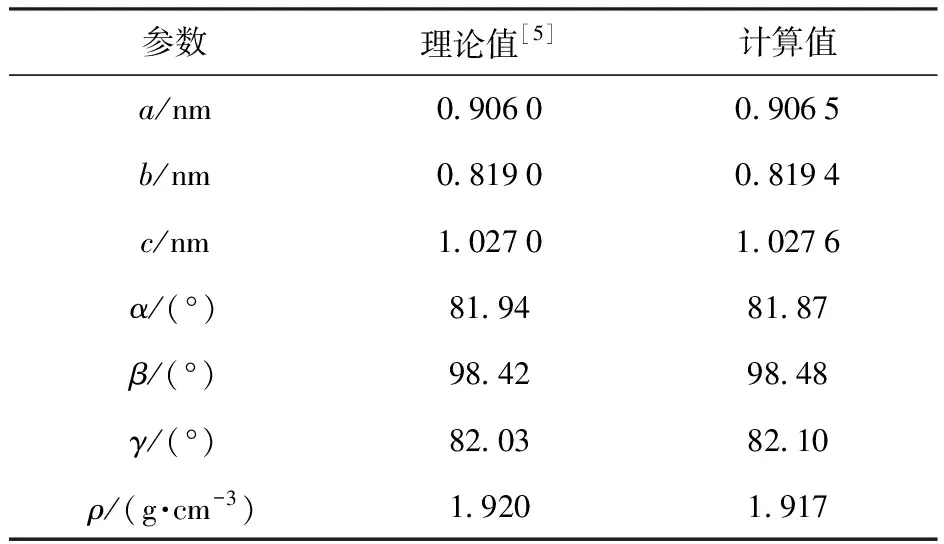
表1 HMX/NTO晶胞参数与密度的计算值与理论值

2.2 平衡判别和平衡结构

在提取计算结果时，需要让体系达到平衡状态，而体系平衡时必须同时满足温度平衡与能量平衡。通常认为当温度与能量波动范围在5%～10%时，体系已经达到热力学平衡状态。

以掺杂率为4.17%的缺陷模型(模型3)为例，模拟过程中混合体系的温度T变化曲线与能量E随时间t变化曲线，如图6所示。

从图6可以看出：在模拟计算初期，体系的温度与能量均有所上升，并且波动幅度较大；随着时间的推移，温度与能量的波动幅度逐渐减小，最终温度波动幅度为±15 K左右，能量波动幅度为±5%左右，偏差相对较小，表明混合体系已达到热力学平衡状态。对于其他晶体模型，分子动力学计算时，均以温度与能量变化曲线来判别混合体系是否达到平衡状态。

2.3 结合能

结合能Eb定义为分子之间相互作用力Ei的负值，主要用来预测体系的稳定性。结合能越大，表明分子之间的相互作用力越强，体系的稳定性越好。

对于HMX/NTO共晶及其缺陷晶体炸药，结合能的计算公式为

Eb=-Ei=-[Etot-(ENTO+Eo)]，

(1)

式中：Etot为混合体系达到热力学平衡状态时对应的总能量；ENTO为去掉体系中的其他组分后，NTO分子对应的总能量；Eo为去掉晶体模型中的NTO分子后，体系中的HMX与其他组分对应的总能量。

根据分子动力学计算得到的各组分能量，通过计算得到不同模型的结合能，结果如图7所示。

从图7可以看出：“完美”型晶体模型(模型1)对应的结合能最大(362.7 kJ/mol)，表明HMX与NTO分子之间的相互作用力最强，炸药的稳定性最好；缺陷晶体的结合能均有不同程度的减小，其中掺杂缺陷晶体模型(模型2)的结合能最大(351.6 kJ/mol)，而空位缺陷晶体模型(模型8)的结合能最小(313.9 kJ/mol)，结合能减小的幅度为3.06%～13.45%. 同时，结合能的变化趋势也表明掺杂缺陷对结合能的影响相对较小，而空位缺陷对结合能的影响最大。此外，从图7还可以看出，对于同种类型的晶体缺陷，随着缺陷数量的增加，结合能逐渐减小，表明分子之间作用力的强度逐渐减弱，炸药的稳定性逐渐减弱，即晶体缺陷会对炸药的稳定性产生不利影响。结合能减小的原因可能是由于缺陷的影响，晶体的结构遭到破坏，分子的排列方式发生了变化，从而使分子之间的作用力减弱。

2.4 感度

感度定义为含能材料在受到外界刺激时发生分解或者爆炸的难易程度，是含能材料安全性的指标，也是含能材料最重要的性能之一。目前，国内外通常采用试验测试与理论分析的方法来预测含能材料的感度。根据热点理论[15]与引发键思想[16]，同时参考以往的研究工作[17-21]，本文中选用引发键键长、引发键键连双原子作用能与内聚能密度(CED)来预测炸药的感度，并评价其安全性。

2.4.1 引发键键长

所谓引发键，是指含能材料中能量最低、最容易发生断裂的化学键。在外界刺激下，引发键更容易发生断裂破坏，从而使含能材料发生分解或爆炸。在HMX/NTO共晶及其缺陷晶体中，HMX所占的比重最高，而HMX的引发键是N—NO2键中的N—N键[16,22-23]。因此，选择HMX分子中的N—N键作为引发键来预测体系的感度。

以模型5为例，图8给出了体系达到平衡状态时引发键的键长分布情况，其中L为键长，P为键长的分布概率。在热力学平衡状态下，不同模型中引发键的最可几键长Lp、平均键长La与最大键长Lmax如表2所示。

表2 不同模型中引发键的键长

从图8可以看出，在平衡状态下，体系中引发键(N—NO2键)的键长分布呈近似对称的高斯分布。从表2可以看出，对于“完美”型与含有晶体缺陷的模型，最可几键长与平均键长近似相等，并且变化范围很小，表明晶体缺陷对最可几键长与平均键长的影响很小，而最大键长变化很明显，且不同模型之间差异较大。“完美”型晶体(模型1)的最大键长最小(0.154 3 nm)，而缺陷晶体的最大键长均大于初始模型对应的键长值，其中掺杂缺陷模型(模型2)的键长最小(0.155 1 nm)，而空位缺陷模型(模型8)的键长最大(0.160 4 nm)，与“完美”型晶体相比，最大键长的增大幅度为0.52%～3.95%. 最大键长增大，表明引发键的键能降低，预示含能材料的感度增大，安全性降低，即晶体缺陷使得炸药的感度升高。此外，表2也表明，空位缺陷的晶体模型对应的引发键键长最大，且随着缺陷数量的增加，最大键长逐渐增大，即炸药的感度逐渐升高，安全性逐渐降低。

2.4.2 键连双原子作用能

键连双原子作用能主要用来反映键的强度，键连双原子作用能越大，表明键的强度越大，键断裂时需要的能量越多，含能材料的感度越低，安全性越好。

键连双原子作用能EN-N的计算公式为

EN-N=(ET-EF)/n，

(2)

式中：ET为体系达到热力学平衡状态时对应的总能量；EF为固定晶体中HMX分子中所有的N原子后体系的总能量；n为体系中HMX分子包含的N—N键的数量。

通过计算，得到不同模型的键连双原子作用能，如图9所示。

从图9可以看出，在不同的晶体模型中，键连双原子作用能的差异较大。其中，“完美”型晶体模型(模型1)的键连双原子作用能最大(160.77 kJ/mol)，而缺陷晶体的键连双原子作用能均小于“完美”型晶体模型对应的键的能量。在缺陷晶体中，掺杂缺陷模型(模型2)的键能最大(156.57 kJ/mol)，而空位缺陷模型(模型9)的键能最小(135.53 kJ/mol)，键连双原子作用能减小的幅度为2.61%～15.70%. 键连双原子作用能减小，表明键的强度减弱，键断裂时需要的能量减小，即含能材料的感度增大，安全性降低。由此可见，晶体缺陷会对炸药的安全性产生不利影响。此外，空位缺陷的模型对应的键连双原子作用能最小，键的强度最弱，感度最高，且随着缺陷数量的增加，键的能量逐渐降低，预示空位缺陷对炸药的感度影响更为显著。之前的研究也表明，由于空位缺陷的影响，在晶体内部容易形成“热点”，从而使含能材料的感度升高，安全性降低[6,24-25]。

2.4.3 CED计算

CED定义为单位体积内1 mol物质由凝聚态变为气态时克服分子间作用力所做的功。CED属于非键力，在数值上等于vdW与静电力之和。

根据计算结果，得到不同模型的CED、vdW与静电力，结果如表3所示。

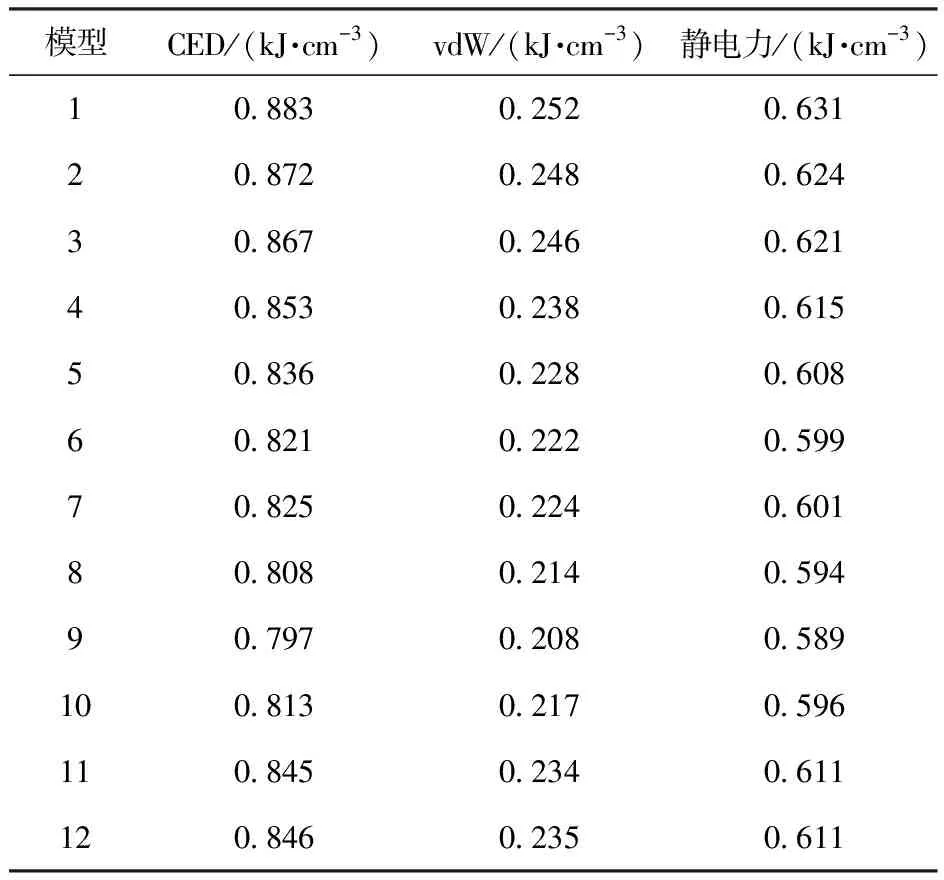
表3 不同模型的CED、vdW与静电力

从表3可以看出，“完美”型晶体模型(模型1)的能量最高，其中CED、vdW与静电力分别为0.883 kJ/cm3、0.252 kJ/cm3、0.631 kJ/cm3，而缺陷晶体的能量均有不同程度的减小。在缺陷晶体中，掺杂缺陷模型(模型2)对应的CED最大(0.872 kJ/cm3)，而空位缺陷模型(模型9)的CED最小(0.797 kJ/cm3)，CED减小的幅度为1.25%～9.74%. CED减小，表明炸药由凝聚态变为气态时吸收的能量减小，预示炸药的感度增大，安全性降低。此外，表3也进一步表明，空位缺陷晶体模型的CED最低，且随着缺陷数量的增加，CED逐渐减小，表明炸药的感度逐渐增大，安全性呈下降趋势。

2.5 爆轰性能

爆轰性能是含能材料威力与能量密度的直接体现，也是武器弹药毁伤效果的直接反映，通常用爆轰参数进行表征。常见的爆轰参数主要有爆速D与爆压p等。本文中采用修正氮当量法[26]来计算炸药的爆轰参数并预测其能量密度。

爆速D与爆压p的计算公式为

(3)

式中：∑Nc为炸药的修正氮当量；di为1 mol炸药爆炸时生成第i种爆轰产物的摩尔数；Ndi为第i种爆轰产物的氮当量系数；BK为炸药分子中第K种化学键出现的次数；NBK为第K种化学键的氮当量系数；Gj为炸药分子中第j种基团出现的次数；NGj为第j种基团的氮当量系数。

根据修正氮当量理论，通过计算得到不同模型的爆轰参数，结果如表4所示，其中炸药密度可以根据分子动力学计算结果从平衡体系中直接提取得到。

表4 不同模型的爆轰参数

从表4可以看出，对于不同的晶体模型，“完美”型晶体模型(模型1)对应的密度、爆速与爆压最大，分别为1.917 g/cm3、8 970 m/s、37.68 GPa，表明“完美”型晶体的威力最大，能量密度最高。在缺陷晶体中，位错缺陷模型(模型12)的密度、爆速与爆压最大，分别为1.904 g/cm3、8 924 m/s、37.16 GPa，而空位缺陷模型(模型8)的密度、爆速与爆压最小，分别为1.802 g/cm3、8 538 m/s、33.03 GPa，密度、爆速与爆压的减小幅度分别为0.68%～6.00%、0.51%～4.82%、1.38%～12.34%. 密度、爆速与爆压减小，表明炸药的威力减小，能量密度降低，因此晶体缺陷会对炸药的能量特性产生不利影响。此外，在3种类型的晶体缺陷中，空位缺陷模型对应的密度、爆速与爆压最小，表明其能量密度最低，也进一步表明空位缺陷对能量密度的影响更为显著。在缺陷晶体中，随着缺陷数量的增加，炸药的密度、爆速与爆压逐渐减小，能量密度逐渐降低。

2.6 力学性能

力学性能主要包括拉伸模量E、剪切模量G、体积模量K、泊松比γ与柯西压C12-C44，其中E、K、G主要用来预测体系的刚性与硬度，其值越大，表明体系的刚性越强，硬度越大。柯西压力主要反映体系的延展性，柯西压力为正值，表明体系的延展性较好；柯西压力为负值，表明体系呈脆性。

力学参数可通过弹性系数矩阵进行描述，表达式[27-28]为

σi=Cijεj，i,j=1,2,…,6，

(4)

式中：σ为应力；ε为应变；Cij为弹性系数，满足Cij=Cji，因此独立的弹性常数只有21个，对于完全的各向同性体，独立的弹性常数只有2个(C11，C22)。

体积模量K与剪切模量G的计算公式为

KR=[S11+S22+S33+2(S12+S23+S31)]-1，

(5)

GR=15[4(S11+S22+S33)-4(S12+S23+S31)+
3(S44+S55+S66)]-1，

(6)

式中：下标R表示Reuss平均；柔量系数矩阵S=[Sij]等于弹性系数矩阵C的逆矩阵，即S=C-1=[Cij]-1.

力学参数之间存在如(7)式的关系：

E=2G(1+γ)=3K(1-2γ).

(7)

基于(7)式，可以求得拉伸模量E与泊松比γ的表达式为

(8)

(9)

通过计算，得到不同模型的力学性能参数，结果如表5与图10所示。

从表5与图10可以看出：“完美”型模型(模型1)的拉伸模量、体积模量与剪切模量的值最大，分别为14.441 GPa、8.773 GPa、5.891 GPa，而柯西压的值最小(0.198 GPa)，表明炸药的刚性最强，延展性与塑性较差；对于缺陷晶体，由于炸药的晶体结构发生了变化，E、K、G减小，而柯西压增大，表明炸药的刚性与硬度减弱，延展性与塑性增强。在外界作用下，炸药更容易发生形变。在缺陷晶体中，掺杂缺陷模型(模型2)对应的E、K、G最大，分别为13.853 GPa、8.518 GPa、5.634 GPa，而空位缺陷模型(模型10)的模量最小，分别为9.325 GPa、5.687 GPa、3.801 GPa. 因此，空位缺陷对炸药力学性能的影响更为显著。此外，从图10还可以看出，对于同种类型的晶体缺陷(掺杂、空位)，随着缺陷数量的增加，E、K、G逐渐减小，而柯西压呈现出增大的变化趋势，预示炸药的刚性减弱，塑性与延展性增强。