带初始前置角和末端攻击角约束的偏置比例导引律设计以及剩余飞行时间估计

马帅， 王旭刚， 王中原， 杨靖

(1.南京理工大学 能源与动力工程学院, 江苏 南京 210094; 2.中国兵器工业第203研究所, 陕西 西安 710065)

0 引言

在导引律的设计中，考虑末端攻击角度约束可显著提高导弹的作战效能和毁伤效果，是导引律研究中的热点问题[1-3]。近年来，随着反导技术的发展，使用单枚导弹攻击配备有密集导弹防御系统的地面目标或海面舰艇时，导弹突防显得愈发困难，而多导弹协同攻击以其特有的优势能够极大地提高突防概率。相对于使用独立的单枚导弹攻击目标，使用多枚导弹同一时间从不同方向协同攻击目标是一种更有效的攻击策略。导弹间的时间协同需要每枚导弹的飞行时间估计值，估计值的准确性将对导弹间的协同攻击产生很大影响。因此，研究考虑末端攻击角度约束的导引律以及精确的剩余飞行时间估计方法具有重要意义[4-9]。

考虑末端攻击角度约束的导引律设计有很多方法，如偏置比例导引律、基于最优控制理论进行设计、基于滑模控制理论进行设计等[10]。与其他设计方法相比，偏置比例导引律结构简单，所需的信息量少[11]，更易于工程实现。Kim等[12]最早使用偏置比例导引对末端攻击角度约束问题进行研究，设计了一种将剩余飞行距离函数作为时变偏置项的导引律。Lee等[1]基于比例导引律和末端攻击角度误差反馈设计了一种不包含线性近似项的导引律，该导引律中含剩余飞行时间项，需对导弹飞行时间进行精确估计。高峰等[13]为了增大反坦克导弹命中落角，设计了一种基于落角约束的偏置比例导引律，该导引律同样包含剩余飞行时间项。以上3种导引律因需要剩余飞行时间估计或者弹目间距等信息，在实际应用中难以实现[14]。Zhang等[3]针对大末端攻击角度约束问题，设计了一种偏置比例导引律，该导引律不需要剩余飞行时间估计，且在初始前置角小于π/2 rad时，能够满足任意的末端攻击角度约束要求，但若导弹受到干扰，导致前置角大于π/2 rad，则该导引律是否适用仍需开展分析。Kim等[14]基于两阶段导引方案，提出了一种偏置项成型的导引方法，该方法需要对偏置项进行积分，且该导引律结构复杂，不利于实际应用。

针对剩余飞行时间估计问题，很多学者做了相关研究。Jeon等[5]基于小前置角假设，给出了比例导引律的剩余飞行时间估计公式。Lee等[1]在初始视线坐标系内基于小航向角假设，推导了带有误差反馈比例导引律的剩余飞行时间估计公式。张春妍等[15]同样基于小前置角假设，推导了带有落角约束偏置比例导引律的剩余飞行时间估计公式。以上方法均基于小角度假设，这些方法在用于大前置角时估算精度不高，且当指定的末端攻击角度增大时，飞行时间估计误差也会增大[3]。Dhananjay等[16]针对比例导引律给出了精确的剩余飞行时间估计方法。Cho等[17]基于高斯超几何函数同样给出了纯比例导引的剩余飞行时间解析表达式。为了精确地估算剩余飞行时间，Tahk等[18]提出了一种递归的飞行时间计算方法，该方法首先计算最小的剩余飞行时间，然后递归地补偿由路径曲率产生的时间误差。针对大前置角下偏置比例导引律剩余飞行时间估算问题，由于难以直接求得解析解，且不能使用小角度近似，文献[3,19]采用数值求解方法，基于分段迭代求解思想和泰勒级数展开，推导了比例导引律和大攻击角度约束下带有末端攻击角度约束的偏置比例导引律的剩余飞行时间估计算法。该算法可根据自定义小角度的取值来调整轨迹分段数，从而调整飞行时间估计精度和总计算量，估计误差小，误差收敛快。但该算法在前置角等于π/2 rad时存在奇点，若导弹受到干扰，导致前置角大于π/2 rad，则如何对该算法进行拓展仍需开展研究。

本文针对导弹飞行过程中受到外部干扰导致前置角变化较大的问题，研究了考虑末端攻击角度约束的偏置比例导引律设计以及剩余飞行时间估计问题。本文创新点如下：1)设计了满足任意初始航向角和末端攻击角度约束的偏置比例导引律(MBPNG_IAC)，并对该导引律下系统参数的收敛性给出了证明；2)对于文献[3]提出的剩余飞行时间估计算法在前置角等于π/2 rad存在奇点问题，本文对该算法进行了拓展，使其适用于前置角属于[-π rad,π rad]的飞行环境，采用参考文献[3,19]的方法，给出了本文提出导引律的剩余飞行时间估计。

1 MBPNG_IAC设计

1.1 弹目相对运动模型

导弹与目标的相对运动关系如图1所示：Oxy为惯性坐标系，M为导弹位置，T为目标位置，R为导弹与目标间的距离，v为导弹速度，an为导弹的法向加速度；θ为导弹的航向角，规定由水平基线逆时针转到导弹速度方向为正；q为弹目视线角，规定由水平基线逆时针转到视线方向为正；φ为导弹的前置角，规定由导弹速度方向逆时针转到视线方向为正；θd为指定的末端航向角。

弹目相对运动方程为

(1)

(2)

(3)

q=θ+φ.

(4)

在初始时刻t0时，各参数初值为R(t0)=R0，φ(t0)=φ0，q(t0)=q0，θ(t0)=θ0.

记tf为终端时刻，每一时刻导弹的剩余飞行时间tg定义为

tg=tf-t.

(5)

tg无法通过仪器测量得到，需要对其进行估计，每一时刻的剩余飞行时间估计值记为g.

1.2 任意初始前置角和末端攻击角度约束下的偏置比例导引律

针对导弹飞行过程中受到外部干扰导致前置角变化较大的问题，本文设计的形式为：

1)若α0≥0°，则导引律为

(6)

式中：N为导航系数，取N≥3；K为常量，取1≤K≤N-1；α为自定义角度，表达式为

α=(1-N)q+(N-1)θd-φ.

(7)

2)若α0<0°，则导引律为

(8)

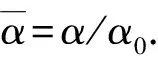
将(6)式、(8)式代入(1)式～(4)式，可得

1)若α0≥0°且φ∈(-π/2 rad,π rad]，或α0<0°且φ∈[-π rad,π/2 rad)，则有

(9)

2)若α0≥0°且φ∈[-π rad,-π/2 rad]，或α0<0°且φ∈[π/2 rad,π rad]，则有

(10)

2 使用MBPNG_IAC时系统参数收敛性证明

本文提出的MBPNG_IAC根据α0和φ所属范围进行切换，本质上是两种导引律形式，即

(11)

(12)

MBPNG_IAC在前置角属于(-π/2 rad,π/2 rad)时，采用的导引律(11)式与文献[3]中提出的适用于大攻击角度约束的偏置比例导引律(BPNG_IAC)相同。文献[20]对导引律(11)式在前置角属于(-π/2 rad,π/2 rad)时进行了分析，证明了该导引律下系统参数的收敛性，证明过程可参见文献[20]。

引理[10,20]若初始前置角满足|φ(t0)|<π/2 rad，则使用导引律BPNG_IAC的导引系统从某种意义上来说是有限时间收敛的，它满足：

1)对于t∈[t0,tf]，R(t)≤R(t0)∧R(tf)=0 km；

2)对于t∈[t0,tf]，|φ(t)|<π/2 rad∧φ(tf)=0 rad；

3)对于t∈[t0,tf]，|α(t)|≤|α(t0)|∧α(tf)=0°.

对于本文提出的导引律，只要证明当前置角大于π/2 rad时，前置角能收敛至区间(-π/2 rad,π/2 rad)，由上述引理，即可证明使用本文提出的导引律系统参数也是收敛的。

对于前置角大于π/2 rad，以下分4种情况对前置角的收敛性进行分析。

1)α0≥0°且φ0∈[π/2 rad,π rad]。

由(9)式可知，当φ∈[π/2 rad,φ0]时，有dα/dt≥0、dφ/dt<0，当且仅当φ=π/2 rad时dα/dt=0. 因此，该段内α单调递增，φ单调递减至π/2 rad. 设ε为无限趋近于0的正常数，当φ=π/2-ε时，有

(13)

ε取足够小，区间[π/2-ε,π/2 rad]内必有dφ/dt<0，该情况下前置角必定单调收敛至区间(-π/2 rad,π/2 rad)。

2)α0≥0°且φ0∈[-π rad,-π/2 rad]。

由(10)式可知，当φ∈[φ0,-π/2 rad]时，有dα/dt≤0、dφ/dt>0，当且仅当φ=-π/2 rad时dα/dt=0. 因此，该段内α单调递减，但仍满足α≥0，φ单调递增至-π/2 rad. 当φ=-π/2+ε时，有

(14)

区间[-π/2 rad,-π/2+ε]内必有dφ/dt>0，该情况下前置角必定单调收敛至区间(-π/2 rad,π/2 rad)。

3)α0<0°且φ0∈[π/2 rad,π rad]。

由(10)式可知，当φ∈[π/2 rad,φ0]时，有dα/dt≥0，dφ/dt<0，当且仅当φ=π/2 rad时dα/dt=0. 因此，该段内α单调递增，但仍满足α≤0°，φ单调递减至π/2 rad. 当φ=π/2-ε时，有

(15)

区间[π/2-ε,π/2 rad]内必有dφ/dt<0，该情况下前置角必定单调收敛至区间(-π/2 rad,π/2 rad)。

4)α0<0°且φ0∈[-π rad,-π/2 rad]。

由(9)式可知，当φ∈[φ0,-π/2 rad]时，有dα/dt≤0，dφ/dt>0，当且仅当φ=-π/2 rad时dα/dt=0. 因此，该段内α单调递减，φ单调递增至-π/2 rad. 当φ=-π/2+ε时，有

(16)

区间[-π/2 rad,-π/2+ε]内必有dφ/dt>0，该情况下前置角必定单调收敛至区间(-π/2 rad,π/2 rad)。

综合上述4种情况及引理可知，初始前置角|φ0|≥π/2 rad时，前置角φ先单调收敛至区间(-π/2 rad,π/2 rad)，之后一直维持在区间(-π/2 rad,π/2 rad)内。因此，使用本文提出的导引律，系统参数也是收敛的。

对于上述4种情况，若前置角满足|φ(t)|≥π/2 rad，则α符号不变。对于前置角φ∈(-π/2 rad,π/2 rad)时，由(9)式、(10)式分析可知，无论α为正或负，α均单调趋近于0°，即对于前置角φ∈(-π/2 rad,π/2 rad)时，α符号仍不变。因此，使用本文提出的导引律，整个飞行过程α不变号，且在飞行末端α收敛至0°，这也是1.2节只需根据α0的正负性来判定使用哪种导引律的原因。根据φ和α的变化情况以及(9)式、(10)式可知，弹目间距R在前置角|φ(t)|>π/2 rad时单调递增，在|φ(t)|=π/2 rad时取极大值，之后|φ(t)|<π/2 rad弹目间距单调递减，直至飞行末端收敛至0 km. 由(8)式可知，飞行末端攻击角度收敛于指定的航向角θd，即该导引律在前置角属于[-π rad,π rad]时，能够满足任意指定的末端攻击角度约束要求。

3 使用MBPNG_IAC时剩余飞行时间估计方法

大攻击角度约束下的偏置比例导引律不能使用小角度假设，且解析求解困难。针对该问题，文献[3，19]采用分段求解思想，对前置角的变化区间进行分段，保证每一段内前置角的变化量都是小角度，通过泰勒级数展开对每段内的微分方程进行求解，每段内的估计时间相加，即可得到总的剩余飞行时间估计值。该方法虽适用于大前置角下求解且求解精度较高，但在前置角等于π/2 rad时存在奇点，无法对前置角大于π/2 rad的情况进行求解。本节基于该方法进行拓展，得到了一种适用于前置角大于π/2 rad的剩余飞行时间估计算法。

定义小角度Ω(Ω>0°)，当初始前置角φ0满足|φ0|>π/2 rad时，将飞行过程分为3段，分别记为D1、D2和D3，3段对应的前置角区间分别为 |φ|>π/2+Ω、π/2-Ω≤|φ|≤π/2+Ω、|φ|<π/2-Ω.

对于D3段，前置角小于π/2 rad，该段可以采用文献[3]提出的估计算法。本节的重点在于D1段和D2段的剩余飞行时间估计。

3.1 剩余飞行时间估计算法

第2节中已经提到，本文提出的导引律本质上是使用了两种形式的导引律，即(11)式和(12)式。对于(11)式导引律的剩余飞行时间估计，文献[3]进行了详细推导，这里基于文献[3]提出的分段迭代求解思想，首先推导(12)式导引律的剩余飞行时间估计公式。

由(10)式可得

(17)

式中：B1=(N-1)/K.

将D1段所处时间区间[t0,tf]分为m段，即[t0,t1],[t1,t2],…,[tm-2,tm-1],[tm-1,tf]，每一时间段内前置角的变化量均为小角度，即|Δφ|≤Ω. 以第1段[t0,t1]为例，其中t1=t0+Δt1，对于时刻t∈[t0,t1]，前置角

φ(t)=φ0+Δφ(t)，

(18)

Δφ(t)为小角度且Δφ0=Δφ(t0)=0. 使用1阶泰勒级数展开：

tanφ(t)≈tanφ0+Δφ(t)/cos2φ0.

(19)

将(18)式对α求微分，并代入(17)式、(19)式得

d(Δφ)/dα=-B1(tanφ0+Δφ/cos2φ0)/α-1.

(20)

定义变量u，有

u=(tanφ0+Δφ/cos2φ0)/α，

(21)

u在t0时刻的值记为u0，u0=u(t0)=tanφ0/α0.

由(20)式、(21)式得

d(αu)/dα=(-B1u-1)/cos2φ0，

(22)

又

(23)

由(22)式和(23)式得

(24)

令B2=-B1/cos2φ0-1、B3=1/cos2φ0，对(24)式整理得

du/(B2u-B3)=dα/α，

(25)

式中：系数B2<0. 对(25)式积分，得

(26)

将(26)式代入(20)式，可得

(27)

式中：B4=sinφ0cosφ0；B5=α0.

由(10)式得

(28)

对(28)式积分，得

(29)

由(10)式得

(30)

对1/cosφ在φ0处泰勒级数展开，得

1/cosφ≈(1+tanφ0Δφ)/cosφ0.

(31)

将(29)式、(31)式代入(30)式，得

(32)

式中：B6=R0/(Kvcosφ0)；B7=sin2φ0；B8=α0tanφ0.

对(32)式在区间[t0,t0+Δt1]上积分，得

(33)

综上所述可知，使用(12)式导引律时，每段内前置角的变化量、弹目间距值以及飞行时间估计值可由(27)式、(29)式和(33)式得到。

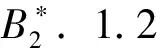
为了算法的完整性，直接给出使用(11)式导引律时每段内的参数估计表达式，即

(34)

(35)

(36)

由(27)式、(29)式、(33)式、(34)式、(35)式和(36)式，得到了D1段和D3段内每一小分段的参数估计表达式。对于D2段，有π/2-Ω≤|φ|≤π/2+Ω，当|φ|=π/2 rad时，不能再使用上述分段迭代求解方法。Ω为小角度，因此cos(π/2±Ω)≈cos (π/2)=0. 对D2段采用小角度近似，(9)式、(10)式可近似为

(37)

对于D2段，弹目间距R和角度α变化很小，这里近似当作常量处理，则该段内的飞行时间估计值为

(38)

3.2 剩余飞行时间估计过程

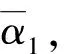
1)α0≥0°且φ0∈[π/2 rad,π rad]。

(39)

整理得

(40)

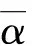
2)α0≥0°且φ0∈[-π rad,-π/2 rad]。

(41)

整理得

(42)

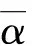
3)α0<0°且φ0∈[π/2 rad,π rad]。

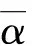
4)α0<0°且φ0∈[-π rad,-π/2 rad]。

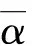
综合上述4种情况可知，当|φ|>π/2 rad时，|Δφ|均从0开始单调递增。

需要注意的是，飞行过程由D1段进入D2段时，必然对应某一时刻的前置角φp满足π/2 rad<|φp|≤π/2+Ω. 该时刻参数可由D1段内最后一段迭代得到，取该时刻参数αp和Rp，由(38)式估算D2段内的飞行时间。D3段从|φ|=π/2-Ω开始，初始参数仍为αp和Rp，初始前置角为φ=π/2-Ω或φ=-π/2+Ω，继续按D1段内的迭代方法进行求解，直至整个飞行过程结束。D1段和D3段内为保证前置角的变化量为小角度，对飞行过程进行了分段，而D2段作为一个整体进行求解。定义D1段和D3段内的分段数之和为n，总飞行时间估计值由各段飞行时间估计值求和得到。

4 仿真分析

4.1 MBPNG_IAC的有效性验证

前置角小于π/2 rad时，本文提出的导引律同文献[3]中的导引律，该导引律在不同末端约束角下的有效性已经得到了理论证明和仿真验证。因此本节主要针对初始前置角大于π/2 rad的飞行环境，取不同的末端攻击角度对本文提出导引律的有效性进行验证。

假设目标静止，坐标为(0 km, 0 km)，导弹初始坐标为(-10.0 km, 0.5 km)，速度取为常量250 m/s，初始航向角取为150°，末端攻击角度分别为0°、±60°、±120°和180°. 导航系数取N=3，系数取K=2. 考虑到导弹的加速度饱和，最大法向加速度取为5g，g为重力加速度。使用本文提出的导引律进行二维仿真分析，仿真结果如图2～图7所示。

由图2可知，导弹的初始航向角取为150°时，对于不同的末端攻击角度，导弹均能命中目标。图3中，末端攻击角度θd为60°、120°和180°时，加速度指令在0～20 s内均达到了两次饱和。对比图2可知，0～20 s内这3种末端攻击角度情况下的飞行轨迹曲率半径小，因此需要更多的法向加速度用于改变飞行方向，这与图3中加速度指令饱和的结果吻合。由图3还可知，加速度指令在飞行末端收敛至0. 图4中，末端航向角均达到了指定角度。由图5可知，前置角首先单调收敛至区间(-π/2 rad,π/2 rad)，之后一直保持在该区间内，这与第2节中前置角的变化规律分析结果吻合。由图6可知，自定义角α最终收敛至0°，且整个飞行过程中α符号不变。图7中，因初始前置角大于π/2 rad，弹目间距先单调递增至极大值，在极大值附近变化缓慢，之后前置角小于π/2 rad，弹目间距单调收敛至0 km.

图8和图9分别为初始航向角取90°和120°时的飞行轨迹曲线。由图8和图9可知，对应这两组初始航向角，导弹均能命中目标，同样验证了本文提出导引律的有效性。

4.2 MBPNG_IAC与文献[3]和文献[13]中提出的导引律在前置角大于π/2 rad时的仿真结果比较

文献[3]提出的BPNG_IAC，由于飞行时间估计算法的需要，在偏置项中加入了前置角的余弦，使前置角属于开区间(-π/2 rad,π/2 rad)[3]，该导引律是否适用于前置角大于π/2 rad的情况，仍需开展研究。

文献[1]、文献[13]和文献[15]推导了带有末端攻击角度约束的偏置比例导引律(BPNG)，对于攻击静止目标，以上3篇文献提出的导引律结构是相同的。该类导引律含剩余飞行时间估计，文献[13]将飞行时间估计近似取为弹目间距与导弹速度的比值，得到的导引律用于单枚导弹制导且不考虑攻击时间约束时，对导弹脱靶量和命中落角精度没有明显影响[13,15]。本文对文献[13]提出的偏置比例导引律在前置角大于π/2 rad时的适用情况进行分析。

导弹初始航向角取为150°，末端攻击角度分别取±60°和±120°. 对文献[3]、文献[13]以及本文提出的导引律进行仿真分析，导弹飞行轨迹如图10～图13所示。

图10为末端攻击角度θd=60°时3种导引律对应的飞行轨迹，该情况下，BPNG_IAC失效，而另外两种导引律均能以期望角度命中目标，且BPNG下飞行轨迹较MBPNG_IAC轨迹短。图11为末端攻击角度θd=-60°时3种导引律对应的飞行轨迹，该情况下，BPNG_IAC失效，另外两种导引律均能以期望角度命中目标，且飞行轨迹接近。图12为末端攻击角度θd=120°时3种导引律对应的飞行轨迹，该情况下，3种导引律均能以期望角度命中目标，BPNG下飞行轨迹较另外两种导引律的飞行轨迹长。图13为末端攻击角度约束θd=-120°时3种导引律对应的飞行轨迹，该情况下，BPNG失效，而另外两种导引律飞行轨迹完全相同。

综上所述可知，本文提出的导引律MBPNG_IAC在上述4种情况下均能以预期攻击角度命中目标，而另外两种导引律则不能同时满足要求。因此，相较于另外两种导引律，本文提出的导引律更适用于前置角大于π/2 rad的飞行环境。

4.3 初始前置角大于π/2 rad时MBPNG_IAC的剩余飞行时间估计精度分析

针对文献[3]提出的剩余飞行时间估计算法在前置角等于π/2 rad存在奇点的问题，本文对该方法进行了拓展，使之能够适用于前置角大于π/2 rad. 使用该估算方法对本文提出的导引律进行剩余飞行时间估计，仿真参数同4.1节，指定的小角度Ω取10°. 仿真结果如图14～图17所示。

图14为不同末端攻击角度下的剩余飞行时间实际值与估计值比较，其中实线代表实际值，符号线代表估计值。图15和图16为对应不同末端约束角下的飞行时间估计误差和误差百分比。初始航向角取150°：当末端攻击角度取0°时，最大估计误差为0.60 s，误差百分比为0.88%；当末端攻击角度取60°时，最大估计误差为1.74 s，误差百分比为2.49%；当末端攻击角度取-60°时，最大估计误差为-0.81 s，误差百分比为-0.90%；当末端攻击角度取120°时，最大估计误差为3.51 s，误差百分比为4.17%；当末端攻击角度取-120°时，最大估计误差为-1.07 s，误差百分比为-1.17%；当末端攻击角度取180°时，最大估计误差为6.81 s，误差百分比为6.63%.

综合上述分析可知，该估算方法估计误差较小且误差收敛快，该方法可用于前置角大于π/2 rad时的剩余飞行时间估计。

图17为整个飞行过程中的飞行轨迹分段数。在飞行初期分段数最大，之后逐渐减小直至飞行末端为1. 图17中，对应8～18 s之间，有一小段分段数保持不变。该段为第3节中定义的D2段，由小角度假设得到且当作一个整体来处理，因此D2内轨迹的分段数n在飞行过程中保持不变。小角度Ω的取值也会影响飞行轨迹的分段情况，Ω越小，飞行时间估计误差越小，但飞行轨迹的分段数会增大，计算量也会增加。图18和图19为Ω取5°时的仿真结果，仿真结果验证了上述分析。

5 结论

本文针对导弹飞行过程中受到外部干扰导致前置角变化较大的问题，设计了满足任意初始前置角和末端攻击角度约束的偏置比例导引律，并且证明了该导引律下系统参数的收敛性。对现有分段迭代求解剩余飞行时间方法进行拓展，解决了该方法在前置角等于π/2 rad存在奇点的问题，并用该改进方法给出了该导引律的剩余飞行时间估计。仿真结果表明:

1)本文提出的导引律能够满足任意初始前置角和末端攻击角度约束下的脱靶量和末端角度要求，与以往研究结果相比，该导引律在前置角大于π/2 rad时能够实现对导弹的有效控制。

2)本文改进的飞行时间估算方法可用于前置角大于π/2 rad时的飞行时间估算，估算精度较高且误差收敛快。