基于假三元模型的透辉石-硬玉固溶体热力学性质计算

2019-02-14陆现彩

岩石矿物学杂志 2019年1期

刘鑫，陆现彩

(内生金属矿床成矿机制研究国家重点实验室，南京大学地球科学与工程学院，江苏南京 210023)

矿物的晶体化学特征反映了其形成的物理化学条件，矿物固溶体更是记录了丰富的成因信息，综合分析矿物的晶体化学变化和热力学性质，可重建成岩成矿过程的物理化学条件。在变质岩石学研究中，目前有两种主要方法估算变质作用的温度和压力条件：传统矿物温压计和视剖面图温压计(Powell and Holland， 2008；吴春明等， 2013；吴佳林等， 2015)。与传统矿物温压计仅仅利用实验标定的矿物对或组合推测温度压力不同，视剖面图方法以热力学基本方程为基础，利用矿物固溶体热力学数据库对特定全岩成分进行视剖面图计算，可以得到矿物共生组合、矿物相丰度、成分以及温度压力条件等丰富的信息，是目前研究变质作用物理化学条件和精细过程的最佳方法之一(Powelletal.， 1998； Powell and Holland， 2008；魏春景等， 2009；吴佳林等， 2015)。Powell等(1998)开发了用于计算视剖面图的Thermocalc程序并建立了热力学数据库，前人先后提出了多种成分-活度模型，并用于变质作用的精细研究。但是由于地质过程的复杂性和固溶体矿物的多样性，现有矿物热力学数据库远远不够完善。研究矿物固溶体热力学性质的传统方法主要依靠化学分析和量热学，基于有限的不连续实验数据拟合热力学曲线，固有的实验误差和广泛存在的动力学效应会显著降低热力学参数的准确性。鉴于实验方法的局限性，过去几十年内建立了多种矿物固溶体热力学性质研究的理论计算方法，然而这些方法建立的矿物固溶体模型很难同时考虑长程有序效应(long-range order, LRO)和短程有序效应(short-range order, SRO)。为了弥补这一不足，往往需要知道足够多的原子间相互作用能，并且结合原子分布获得固溶体的最低自由能，因而需要海量的构型计算，而巨大的计算量和高昂的计算成本大大制约了这些理论方法的应用和推广。

本文介绍了一种全新的用于矿物固溶体热力学性质计算的假三元模型，该模型同时考虑了LRO和SRO效应，仅仅通过少量构型计算即可获得精细的固溶体热力学数据，能够准确预测矿物相变边界。本文将该方法用于研究榴辉岩中透辉石-硬玉固溶体系列的热力学性质。榴辉岩是一种标志性高级变质岩，具有鲜明的构造成因意义(陈意等， 2005；魏春景等， 2009；张丽娟等， 2018)，分析榴辉岩中的矿物固溶体体系的晶体化学特征，可利用视剖面图方法重建榴辉岩形成的温度压力条件(Greenetal.， 2007；魏春景等， 2009)，为地球动力学和构造环境研究提供关键数据。

1 模型和方法

1.1 假三元模型

将一种固溶体矿物的分子式写为MR，其晶格中有数量相同的两种阳离子位点(或者人为地分为两种)，记为α和β位点，都可被M1和M2两种阳离子占据。假设一个固溶体具有这种结构，并且包含A和B两种阳离子，则两个端员矿物为AR和BR，其中A和B都可以占据 α和β两种位点。可在二元固溶体端员(AαAβ)R2和(BαBβ )R2之间考虑一个(AαBβ)R2端员作为中间有序态(图1)，这个相可以是自然存在的矿物，也可以仅仅是一种有序态。假如3个端员组分的浓度分别标记为x1、x2和x3，则存在：

x1+x2+x3= 1

(1)

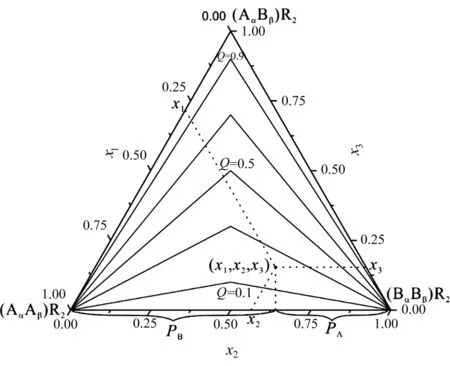
图 1 二元固溶体的假三元模型Fig. 1 Fictive ternary model for binary solid solution

由于仅存在2个独立端员，引入的(AαBβ)R2端员是为了在规则固溶体模型中引入LRO参数Q，该组分也可以使用两端员摩尔分数PA和PB和分子式APABPBR 表示。那么，(x1,x2,x3)和(PA,PB)的关系如下：

PA=x3/2+x1

(2)

PB=x3/2+x2

(3)

如果PAα和PAβ分别是两种阳离子位点A原子出现的概率(B原子同理)，应同时满足：

PAα=x1+x3

(4)

PAβ=x1

(5)

PBα=1-PAα=x2

(6)

PBβ=1-PAβ=x2+x3

(7)

Q=(PAα-PAβ)/(PAα+PAβ) =x3/2PA(PB≥0.5)

(8)

Q=(PBβ-PBα)/(PBα+PBβ)=x3/2PB(PB≤0.5)

(9)

有序度Q的变化范围是[0, 1]。Q=1意味着某个组分固溶体的最有序状态，其组分组成只能沿着图1所示三角形的2个腰边[分别为(AαAβ)R2-(AαBβ)R2连接线和(BαBβ )R2-( AαBβ )R2连接线]变化，A和B原子在α和β位置的占据上具有明显的选择性，总是尽可能先占据满其中一种位置。Q=0意味着PAα=PAβ和PBβ=PBα，也就是说，A和B原子在α和β位置完全无序分布，组分沿着图1三角形的底边[(AαAβ )R2-(BαBβ )R2两个端员的连接线]变化。x=0.5和Q=1则对应完全有序中间态。

根据亚规则固溶体的Bragg-Williams(BW)模型(Bragg and Williams， 1934， 1935)，固溶体的混合焓可以表示如下：

Hmix=PAαPBα(PAαWAα+PBαWBα)+PAβPBβ(PAβWAβ+
PBβWBβ)+PAαPBβWαβ+PAβPBαWβα

(10)

这里的W都是Margules能量参数，W可解释为有序态的焓相对于两个端员AR和BR的机械混合焓的增量，即Wαβ=ΔHord。将(4)～(7)式代入(10)式后化简可得：

Hmix=x1x2[x1(WAα+WAβ+Wαβ+Wβα)+x2(WBα+
WBα+Wαβ+Wβα)]+x1x3(x1WAβ+x3WBβ)+x2x3
(x2WBα+x3WAα)+x3Wαβ+x1x2x3(2WAα+2WBβ+
Wαβ+Wβα)

(11)

同时，定义以下等式：

WAα+WAβ+Wαβ+Wβα=W121

(12)

WBα+WBβ+Wαβ+Wβα=W121

(13)

WAB=W131，WBβ=W133，Wβα=W232，WAα=W233

(14)

2WAα+2WBβ+Wαβ+Wβα=W123

(15)

这样，式(11)可以改写为：

Hmix=x1x2(x1W121+x2W122)+x1x3(x1W131+

x3W133)+x2x3(x2W232+x3W233)+x3ΔHord+

x1x2x3W123

(16)

这就是三元体系的亚规则固溶体模型混合焓表达式，适用于热力学性质不对称的体系。研究表明(Liuetal., 2019)，该表达式会显著高估混合焓和有序-无序相变边界，可对最后一项引入校正因子K解决：

Hmix=x1x2(x1W121+x2W122)+x1x3

(x1W131+x3W133)+x2x3(x2W232+x3W233)+x3ΔHord+

Kx1x2x3W123

(17)

值得说明的是，K因子的引入，并不会影响任意二元体系(x1、x2和x3其中一个为0，对应于图1三角形的3条边)的焓效应，这也是引入该因子的前提。当K从1变化到0时，基于该展开式的计算结果与实验结果吻合度越来越高，根本原因在于BW模型没有考虑短程有序效应，因子K的引入和最后一项的消失，相当于对SRO效应校正，混合焓展开式为：

Hmix=x1x2(x1W121+x2W122)+x1x3(x1W131+x3W133)

x2x3(x2W232+x3W233)+x3ΔHord

(18)

值得注意的是，原本设定的LRO参数Q在经过校正之后携带了SRO效应信息，因此本方法的Q综合反映了LRO和SRO效应，很难将两者完全区分开。最后，BW模型下的每摩尔可交换原子的构型熵应该采取以下形式：

Sconf=-R(PAαlnPAα+PBαlnPBα)/2-
R(PAβlnPAβ+PBβlnPBβ)/2

(19)

这样，结合式(18)和(19)，可以写出自由能的表达式：

Gmix(Q,x,T) =Hmix-TSconf

(20)

式(20)表明，当温度和组分固定时，一定存在有序度Qeq，使得自由能最小。这个最小自由能即为固溶体的混合自由能。因此用Qeq表示的平衡自由能、熵和焓可用以下方程表示：

Gmix(x,T)=Geq(Qeq,x,T) =min[G(Q,x,T)]

(21)

Smix(x,T)=Seq(x,T)

(22)

Hmix(x,T)=Gmix(x,T)+TSmix(x,T)

(23)

至此，矿物固溶体的所有混合热力学性质均可通过组分、温度、有序度Q和Margules参数计算，其中Margules参数能够使用经验势或第一性原理方法计算。

1.2 Margules参数的计算

在计算中需要6个Margules参数：W121、W122、W131、W133、W232和W233，可以通过单缺陷构型方法(single-defect method, SDM)和准随机构型计算(quasi-random Structure, QRS)两种策略(Sluiter and Kawazoe， 2002； Vinogradetal.， 2006； Vinogradetal.， 2013)获得。所谓的随机结构就是离子自由排布的构型，这对于非常大的晶胞很容易实现。然而，在超胞大小受限的计算中，获得完全随机的构型异常困难，只能用尽可能随机的构型代替，也就是准随机构型，这些准随机构型中可能存在短程有序现象。针对特定组分，计算若干种准随机构型的能量，求其平均后即可用亚规则固溶体模型(式24)的焓拟合Margules参数。

Hmix=x1x2(x1W21+x2W12)

(24)

此外，还需要知道ΔHord，这仅需要计算中间组分的有序结构相对于端员矿物的机械混合焓的增量就可以获得。

1.3 透辉石-硬玉固溶体系列的计算

在透辉石(diopside， CaMgSi2O6)-硬玉(jadeite， NaAlSi2O6)这种典型的耦合替代型的矿物固溶体中，存在两种阳离子位置(图2)，较小的M1位置可以被Mg2+和Al3+占据，较大的M2位置可以被Ca2+和Na+占据，具有C2/c空间群。透辉石的一对Ca2+和Mg2+可以被一对Na+和Al3+替代而成为硬玉。该体系中存在中间相矿物绿辉石(omphacite， Ca0.5Mg0.5Na0.5Al0.5Si2O6)，在低温下具有典型的有序结构，也就是说 M1和M2可以被细分为M11、M12、M21和M22等4种亚位置，依次被Mg2+、Al3+、Ca2+和Na+完全占据，具有P2/n空间群。考虑到发生了耦合替代，这4个亚位点可以被重新分为两类，一类包括M11和M21，另一类包括M12和M22，前者可以组合标记为α位置，后者可以组合标记为β位置。这样，绿辉石的分子式可写作[Ca0.5Mg0.5]α[Na0.5Al0.5]βSi2O6，作为透辉石(端员1)和硬玉(端员2)的中间相(端员3)，从而建立了该体系的假三元模型。在高温下，绿辉石晶胞的M11、M12、M21和M22等4种亚位置两两等价，可以看做只有M1和M2两种阳离子位置，具有C2/c空间群。

图 2 透辉石-硬玉固溶体的晶胞结构(蓝色为Si—O四面体，浅蓝色为M1八面体位置，可以被Mg2+和Al3+占据，黄色为M2多面体位置，可以被Ca2+和Na+占据)Fig. 2 Unit cell of diopside-jadeite solid solution (Si—O tetrahedrons are blue, M1 octahedrons are light blue which can be occupied by Mg2+ and Al3+; M2 polyhedrons are yellow, which can be occupied by Ca2+ and Na+)

由于α和β位置为组合所得，只能利用准随机结构来获得Margules参数。因此，除纯的硬玉、透辉石和绿辉石晶胞外，还需建立一系列的准随机构型。在硬玉-透辉石、硬玉-绿辉石和绿辉石-透辉石3个二元固溶体路径上分别选择7、3 和3 个组分点进行计算，计算使用6 × 3 × 3硬玉结构超胞。计算使用GULP 软件包(Gale， 1997, 2005； Gale and Rohl， 2003)，使用的经验势如表1所示(Vinogradetal.， 2007)。为了降低误差，每个组分均选择10个准随机构型进行计算，所有构型能量减去机械混合能后求平均值，再通过拟合亚规则固溶体模型的焓获得Margules参数(表2)，Margules参数拟合效果如图3。

表1 透辉石-硬玉的经验势模型Table 1 Force field parameters for diopside-jadeite system

注：*所有Buckingham势的截断半径都是12 Å。

表 2 透辉石-硬玉固溶体的Margules参数Table 2 Margules parameters for diopside-jadeite solid solution

图 3 透辉石-硬玉体系的Margules参数图解Fig. 3 Margules parameters for diopside-jadeite solid solution

2 结果和讨论

2.1 混合热力学性质

透辉石-硬玉体系混合焓等温线(图4a)具有微弱的不对称性，中间组分的巨大低谷是由于结构中部分有序造成的，而且主要体现为LRO。该体系的构型熵等温线(图4b)显示，273 K下的绿辉石的熵为0，随着温度的升高，熵逐渐增加直到完全无序态的最大值，中间组分的构型熵低谷在1 148 K左右基本消失，对应混合焓的迅速增大，指示了有序-无序相变的发生。在较低温度下，混合自由能等温线(图4c)被有序绿辉石组分分隔成两部分，此时绿辉石的自由能为负值；随温度升高，等温线逐渐变平滑，且所有组分的自由能均具负值。混合自由能的变化一定程度上反映了其稳定性，但对稳定性的准确判断还需公切线分析的相图来说明。

2.2 超额自由能和温度组分相图

在物理化学研究中，通常用超额热力学性质表示实际固溶体和理想固溶体的热力学性质的差值，超额自由能(GE)是应用最广的一个热力学参数，其表达式为：

+(1-x) ln(1-x)]

(25)

透辉石-硬玉固溶体的超额自由能(图5)显示：在1 123 K以下，在绿辉石相的组分附近存在超额自由能的极小值，但是当温度高于1 123 K时，极小值迅速消失。

除超额自由能外，矿物固溶体(A,B)R某端员组分的固相活度系数γ是另外一种常用的热力学参数，与固溶体超额自由能存在如下关系(Redlich and Kister， 1948； Plummer and Busenberg， 1987)：

lnγA=(GE+xB∂GE/∂xA)/RT

(26)

lnγB=(GE+xA∂GE/∂xB)/RT

(27)

尽管有研究认为，晶格内的原子振动对自由能的贡献可以忽略(Bennyetal.， 2009； Ruiz-Hernandezetal.， 2010； Wangetal.， 2011)，但亦有相反的观点(Vinogradetal.， 2007； Liuetal.， 2016)。本研究采用了Vinograd 等(2007)对振动效应的校正公式：

Svib=x1x2(x1S1+x2S2)

(28)

其中，参数S1= 2.5 J/mol·K，S2= 4.5 J/mol·K。经过修正后的该体系的固相活度见图6。

基于自由能等温线，通过公切线分析可得透辉石-硬玉固溶体的温度-组分相图(图7)。对自由能考虑振动效应修正之后(虚线)，相图的温度边界有所降低，透辉石一侧降低100 K左右，而硬玉一侧降低200～300 K。同时可见两个较大的固溶隙，由中间相绿辉石分隔开。富透辉石一侧的固溶隙要比富硬玉一侧略大，相边界温度(～1 623 K)也更高(～1 473 K)，这一认识与前人研究结果一致(Greenetal.， 2007； Vinogradetal.， 2007)。

2.3 绿辉石的有序-无序相变

绿辉石的有序度随温度升高而发生显著的变化(图8)，有序-无序相变发生在1 148±25 K左右(虚线处)，左右两侧分别为P2/n相和C2/c相。结合相图推断此处相变应为一级相变。相变温度与前人实验结果1 138±10 K(Carpenter， 1982)、数学分析结果1 123 K (Greenetal.， 2007)和计算模拟结果1 150±20 K(Vinogradetal.， 2007) 非常相似。需要说明的是，很多研究分别讨论M1和M2两个位置的有序度QM1和QM2，分别提出QM1=QM2(Burton and Davidson，1988； Vinograd， 2002a， 2002b)和QM1=2QM2(Rossietal.， 1983； Vinogradetal.， 2007)两种观点。但是，由于本研究使用的模型相对简单，仅用一个参数表征LRO和SRO。低温下LRO和SRO共存，高温下LRO消失，但是SRO还存在，这也是图8中的有序度不变为零的原因。

图 4 透辉石-硬玉固溶体的混合焓(a)，构型熵(b)和混合自由能(c)等温线(温度范围为273 K到2 073 K，间隔100 K)Fig. 4 Isotherms of enthalpy (a), entropy (b) and free energy of mixing (c) for diopside-jadeite solid solution (The temperature is from 273 K to 2 073 K with a interval of 100 K)

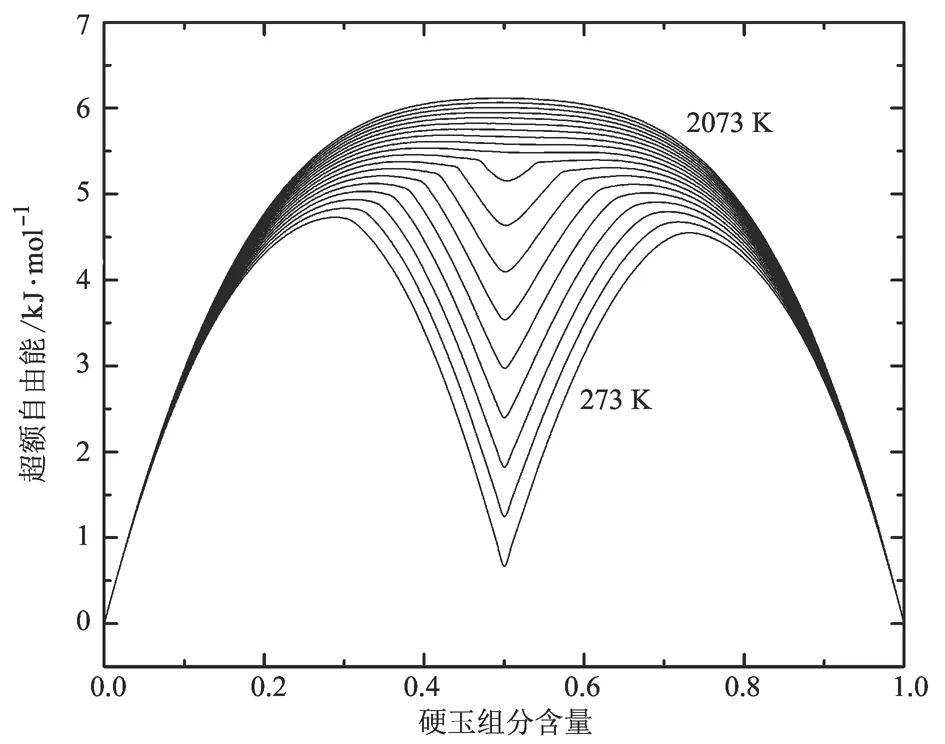
图 5 透辉石-硬玉体系的超额自由能Fig. 5 The excess free energy for diopside-jadeite solid solution

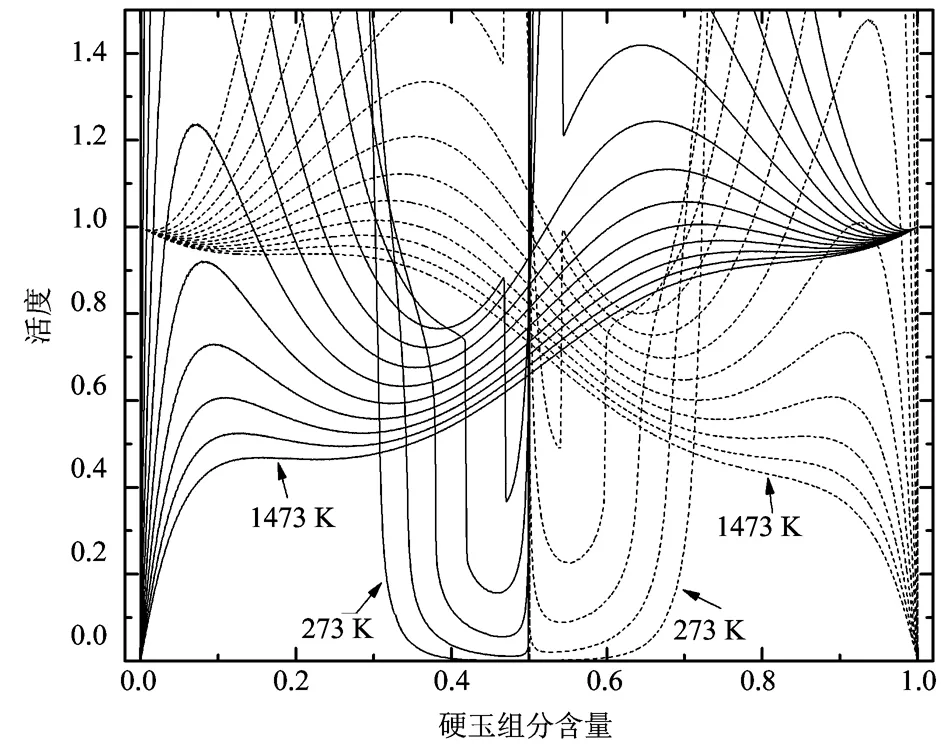
图 6 透辉石-硬玉体系的固相活度(实线和虚线分别表示硬玉和透辉石的活度，间隔100 K)Fig. 6 Activity plots for diopside-jadeite solid solution (The solid lines and dash lines show the activity of jadeite and diopside respectively with an interval of 100 K)

图 7 透辉石-硬玉固溶体的温度-组分相图(实线和虚线分别表示考虑振动贡献修正前后的相边界)Fig. 7 Temperature-composition diagram for diopside-jadeite solid solution(The solid lines and dash lines show the bounda-ries without and with vibrational correction respectively)

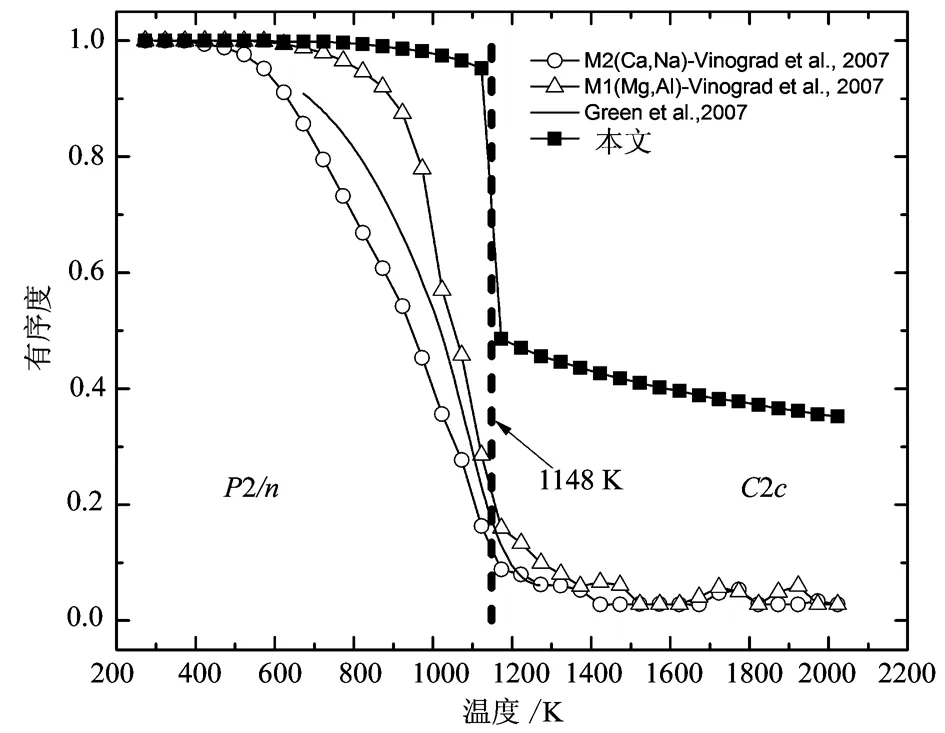
图 8 绿辉石的有序度随温度的变化Fig. 8 Illustration of LRO parameter varying with temperature

2.4 讨论

本研究获得的透辉石-硬玉固溶体的热力学性质数据可以用于相关变质作用的热力学研究，尤其适合MORB成分的榴辉岩相变质作用研究。事实上，研究榴辉岩相变质作用需要多种矿物固溶体的热力学数据，前人已经通过实验和计算的方法得到了石榴子石(Weietal.， 2004)、绿泥石(Hollandetal.， 1998)、单斜辉石(Greenetal.， 2007)、角闪石(Dieneretal.， 2007)、斜长石(Holland and Powell， 1996)等矿物固溶体的热力学参数，但准确性、可靠性和系统性存在显著差异，本文得到的透辉石-硬玉体系的热力学数据较为系统，并且充分考虑了两种有序度，端员组分的参数与前人的数据高度一致，表明可有效补充当前只存在端员组分热力学数据的不足，适用于成分更为复杂含辉石-硬玉体系变质岩的成因研究。

同时，本研究还验证了假三元模型的有效性，该方法具有计算规模小、理论模型简单的特点，可适用于其他相似替代型固溶体系列矿物的研究。这一方法的应用，可以解决当前热力学数据不够系统的现实问题。由于可以避免动力学因素的干扰和实验条件和技术的限制，这一方法至少可以部分替代实验方法的运用，作为实验数据的有效补充，为岩石成因和矿物成因研究提供数据支撑。