程序设计的时间复杂度优化技巧

赵美勇，崔旭冉，宋思睿，汤继澳，王梦媛

（1.山东科技大学，济南 250000；2.上海政法学院，上海 201701）

1 时间复杂的概念

衡量算法占用CPU时间的多少称为时间性能分析，为了便于从算法本质的角度研究算法的时间性能，常通过事前估算的方法，研究算法本身的效率，即研究算法本身的运算量。算法的运算量的大小依赖于问题的规模，则算法的运行时间是问题规模的函数，故常使用函数记录算法的相对运行时间，称为时间复杂度。时间复杂度是一个函数，它表示了一个算法的效率。时间复杂度通常用O表示，形如O（n），其中问题规模n是影响程序运行时间的最主要参数，和程序所需处理的数据量有一定的关系。这样的函数和处理的数据量有关系，而不反映具体运行时间（即函数不反映算法运行的绝对时间），因为具体的因素很多，所以时间复杂度又被称为渐进时间复杂度。数据量是影响算法的一个主要因素，数据量越大时间也就越长，而时间复杂度作为一个函数，被抽象成一个非常简单的形式，其目的就是表示时间效率。不同时间复杂度的算法，其时间和效率的差距是非常大的。

2 常见的几种时间复杂度

时间复杂度的类型往往和程序的循环有关，具体分析如下：

2.1 线性时间复杂度

假设现有下列待执行任务：给定一组数据，并要求找出该数组中数值为1的元素个数。假设该数组的长度为n，那么很容易得到这样一个算法，通过枚举每一个元素的具体数值与数值1进行比较，此枚举算法将执行n次比较操作。对于不同的计算机，这n次操作所需的时间具有一定差异，但是执行的总次数n是确定的。如果此时将这个数组长度变为2*n，即长度变为原来的两倍，那么对应的时间也会增加一倍。诸如此类的算法，其时间复杂度就被称为线性时间复杂度。

2.2 平方时间复杂度

将2.1当中描述的引例做如下修改：现在有两个长度为n的数组，此时需要找到这两个数组里有多少个元素数值相等。这时可以采用以下计算法，首先枚举第一个数组，每次取出一个元素，然后继续枚举第二个数组，将第一个数组和第二个数组中的每一个元素进行比较，对比其数值是否相同。此时最多需要比较n*n次，如果将两个数组都扩大一倍，那么比较次数就变成了4*n*n次，即原来的4倍。诸如此类的算法，其时间复杂度就被称为平方时间复杂度。

2.3 对数时间复杂度

假设现有一个已经排序的长度为n的数组，现在需要找到数组中是否存在一个元素且其值为x。在这里不再使用效率较低的枚举法进行逐项对比。因为数组是已经过排序的，所以每次只需取出当前处于区间最中间位置的元素与数值x进行比较，如果该元素的数值比x大，则向比这个数值更小的方向即左边继续比较，如果数值偏大，以此类推，进行类似的操作逐步比较。这样最多需要比较log（n）次，此时将数组扩大两倍，则需要比较log（2*n）次。诸如此类的算法，其时间复杂度就被称为对数时间复杂度。

3 优化时间复杂度

时间复杂度的优化来源于很多方面，常在编程时利用高级的数据结构、优化核心算法、牺牲空间复杂度等方式来优化时间复杂度，还可利用一些编程过程中的特殊指令等。优化的具体方法如下：

3.1 利用高级的数据结构

利用高级的数据结构主要针对一些需用复杂的数据结构来存储数据的情况，在这种情况下编程人员容易选择一些设计简单但是程序本身运行起来较为复杂的数据结构。此时，根据需求选用一种良好的数据结构来优化时间及效率就显得尤为重要，下面通过一个实例进行说明：假设有这样的一个需求，给定一个元素，要求把该元素放到一个序列的指定位置。此时我们很容易想到建立一个数组，每次插入一个新数据时，将插入的位置后面的元素全部向后平移一个单位以腾出一个位置存放新数据。分析这些操作的时间复杂度可知，设需要操作n次，由于数组刚开始是空的，那么最坏的情况是每次都将新数据插在数组的开头，则总共需要操作n*（1+n）/2次，由此判定是平方时间复杂度。但如果选择链表进行储存，则有以下时间复杂度分析：链表的每次插入操作的时间复杂度为常数即O（1），所以仅仅需要操作n次，即线性时间复杂度，相较原来使用数组，使用链表的时间复杂度明显降低了。

3.2 优化核心算法

这种情况是针对于对于算法设计能力不足，从而导致整个程序的时间复杂度增高，这种情况要求编程者需要极高的算法能力。因此，这通过几个简单的算法优化的例子来说明。

“八皇后”问题是算法设计领域的经典问题，题目大意是，有一个8*8的棋盘，在棋盘上放置8个棋子（“皇后”）使得它们互不攻击，即每次放棋子的时候，需要判断当前的列、行、两条斜对角线是否有棋子，如果有则不能放在这个地方，如果没有则可以放在这个地方，问一共有多少种放法？这个问题看起来实现不难，我们很容易写出以下算法：

算法“八皇后”问题求解

根据上面的算法我们容易直接得到下面的C语言代码：

程序1 算法1的C语言实现（未剪枝）

if（check（））//check方法检查当前棋盘是否符合题目要求

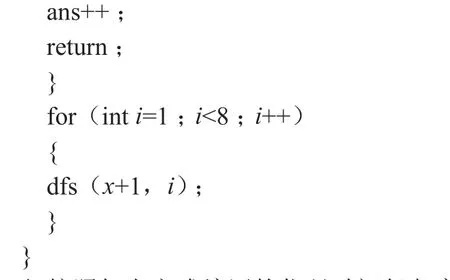
但按照如上方式编写的代码时间复杂度很高，因为此程序会将每一种情况列举出来，然后逐个判断每种情况下的棋盘是否符合要求，由于棋盘是8*8布局，因此一共有88种可能，因此这样的算法时间复杂度是相当高的，所以我们需要优化算法。类似程序1的递归搜索算法，常使用“剪枝”方法进行优化。类似上面的算法，每次递归到某一层，也许当前层的状态已经不符合题目要求了，再怎么扩展也不可能比当前情况更优，没必要继续向下搜索了，就应当强制把它“剪”掉，就像园丁在花园里为树修剪枝叶一样，就可以直接返回结果，此即为剪枝的思想。因此将此程序进行剪枝，如下：

程序2 算法1的C语言实现（剪枝后）

在处理复杂算法时，一定要从整体把握算法的效率，要在适当的位置进行剪枝，否则时间复杂度将会以指数级别增加。

3.3 牺牲空间复杂度

编程人员有时会修改某些数据的存储结构以节省硬盘存储空间，但是缺点显而易见，这样做会导致运算量增大，会增加时间的复杂度。事实上计算机诞生初期其储存空间很小，于是人们会花费更多的时间来寻找更好的算法以处理数据，例如增加一些时间的复杂度来减少空间的复杂度。一个具体的例子是，假设存在一个搜索算法可实现这样的功能，每搜索到一种新情况，即将当前情况保存下来。为此，常见的思路是开辟一个队列以存储数据且节省存储空间，每搜到一种新情况，即令这个新的情况入队。但是运用队列存储时，每次查找过程中需要判断已存储情况与搜索到的新情况是否相同的时候，需要枚举整个队列，显然，此种操作时间复杂度会很高，但是空间复杂度很低。因此为优化时间，可以选择牺牲空间。仍以上述情况为例，可以开辟一个多维数组，每一维都表示情况中的某个条件，这样做虽然会增加很大的空间复杂度，但是每次储存和判断相同情况的时间复杂度都是常数阶的，即可节省大量时间。

对于牺牲空间复杂度的方法，更多的需要结合具体情况。现时计算机硬盘储存容量通常很大，故编程人员可以选择牺牲空间来优化程序运行的时间。通常可以牺牲空间的几种情况如下：大量数据需要判断相等的情况、动态规划问题利用数组来压缩转移方程、区间数组内容的在线修改与查询等，这些问题涵盖了常见的几种需要牺牲空间来优化时间的算法。另举一个具体的例子以展示牺牲空间复杂度方法，现有一种二维的魔方，有三种操作方式，求最少需要多少次操作可以达到某种特定的目标状态。此为经典的广度优先搜索的实例，容易想到开辟一个队列用来存放我们已经搜索过的情况，但是在当前情况入队判断的时候就会遇到本文之前讨论的问题，即判断代价太大，每次枚举队列方式不符合优化时间复杂度的需要。观察可知，二维魔方只有六个格子，每个格子只有三个状态，由于状态量比较小，所以我们可以合理的牺牲空间，故可以开辟一个六维数组，每维数组的长度为3，这样整个空间大小为3的6次方，这样我们就可以利用常数时间复杂度来处理上述情况，大幅度优化了时间复杂度。

4 结束语

上面介绍了有关时间复杂度优化的几种方式，但在真正的程序开发过程中，优化时间复杂度的方法远远不止三种。更多的优化方案还需要来源于日常学习以及实际开发中的经验积累，只有熟练的掌握各种算法，才能在时间复杂度优化方面表现的更出色。现代的计算机配置逐渐走高，时间复杂度优化看似小事，但在程序底层操作时，算法的时间复杂度优化才真正体现出其意义。