基于B样条神经网络算子的散乱数据插值

徐慧芳,曹飞龙

(中国计量大学 理学院,浙江 杭州 310018)

用Rd表示d(d≥1)维欧几里得空间。S={x0,x1…,xn}⊂Rd是由一组两两不同的向量构成的集合,{f0,f1,…,fn}⊂R是一组实数,则

(x0,f0),(x1,f1),…,(xn,fn),

(1)

构成一组插值样本。如果对于任一函数f:Rd→R,有

f(xi)=fi,i=0,1,…n,

则称函数f是一组关于样本(1)的一个精确插值。如果对于给定的ε>0,成立

|f(xi)-fi|<ε,i=0,1,…,n，

则称函数f是关于样本(1)的一个近似插值(拟插值)。

单隐层前馈神经网络的数学模型可表示为

(2)

其中x∈Rd,ci∈R表示隐层与输出层之间的连接权,bi∈R表示阈值,ωi∈Rd表示输入层与隐层之间的连接权,ωi·x表示ωi与x的欧几里得内积,σ(·)是激活函数,通常取为Sigmoid函数,即σ:R→R,且满足

常用的Sigmoid激活函数有

(3)

众知,神经网络是一个万有逼近器,它能够以任意精度逼近定义在紧集上的连续函数或可积函数。在过去的三十年里,人们考虑了形如(2)式且激活函数满足一定条件的神经网络的逼近问题,得到了许多较好的结果(参见文献[1-8])。

插值是一种经典而又非常重要的数据处理方法。与精确插值相比,拟插值具有计算量小,稳定等优点(参见文献[9-10]),同时具有较好的收敛性。2006年,LLANAS和SAINZ[11]首次研究神经网络的插值问题。谢和曹[12]进一步研究了神经网络的拟插值问题。由于在许多实际问题中,我们需要处理高维数据的插值与拟合问题,而传统的插值、逼近方法(如多项式,样条函数,算子等)不能有效地处理这些问题。鉴于前馈人工神经网络的本质是一元函数(激活函数)通过自身的平移、旋转、叠加等产生一个新的多元函数并可以逼近多元函数。因此,利用神经网络插值处理高维数据的插值与逼近是一条有效的途径,特别是对于高维散乱数据。

CHEN和CAO[13]首次将(3)式中的logi-stics函数σl(x)进行变形,得到一个钟型对称函数,并以此为激活函数构造了神经网络拟插值算子,且进一步研究了该拟插值算子的逼近误差。随后,Anastassiou利用这样的钟型函数的乘积,构造了多元算子,并研究该多元算子的逼近误差,其相关的工作可参见文献[14-17]。随后,COSTARELLI和SPIGLER[18],COSTARELLI[19]用满足某种假设的激活函数拓展了相关结果。

迄今,神经网络插值方法大多都是面向规则的节点数据,而在实际中存在大量的非规则数据,即散乱数据。对散乱数据的处理往往相对困难与复杂[20-22]。本文的目的是构建神经网络插值算子并研究散乱数据的插值与逼近问题。我们从B样条函数出发,构造一类具有较好性质的函数,并以此作为激活函数构造神经网络插值算子。进一步地,我们研究了该算子的插值性质与逼近性质，建立了相应的插值与逼近定理。最后,我们给出了数值仿真实验与分析,进一步验证理论结果。

1 预备知识

假设xi∈[-1,1]2⊂R2(i=1,2,…,n)是散乱点,(x1,f1),(x2,f2),…,(xn,fn),构成一组散乱样本。为了描述散乱数据集X:={x1,x2,…,xn},引入网格范数hX、分离半径qX和分离比率ρX等概念[20,22]。

散乱数据集X的网格范数定义为

其中d(x,y)表示点x与y之间的欧几里得距离。易见,hX用来衡量[-1,1]2上的点与数据集X的最大距离。

散乱数据集X的分离半径定义为

其表示数据集X中任意两点之间最小距离的一半。

相应地,散乱数据集X的分离比率ρX定义为

它是用来衡量数据集X中散乱点的均匀分布的程度。易见,ρX≥1。

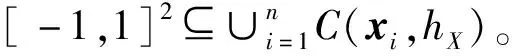
其中C[-1,1]2表示定义在有界域[-1,1]2上所有连续函数的集合,‖·‖2表示欧几里得范数。如果存在一个常数M>0，使得

ω(f,δ)≤Mδα(0<α≤1),

我们就称函数f是Lipschitz-α连续,写成f∈LipMα。函数的连续模是描述函数的光滑性和连续性的量,通常作为度量逼近误差的一个有效工具,其在函数逼近理论中有着非常重要的应用。连续模有如下的一些性质:

1)ω(f,δ)是关于δ的单调增函数,即ω(f,δ)=0,δ→0;

2)ω(f,λδ)≤(λ+1)ω(f,δ),λ≥0。

接下来,我们介绍一维s(s∈N+)阶B样条函数[6,19,24-25]

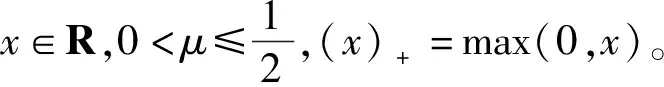
supp(Ms)⊆[-s/2,s/2],s∈N+。

使用上面定义的s阶B样条函数变换出Sigmoid函数σMs(x),即

(4)

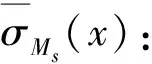
(5)

其中x∈R。

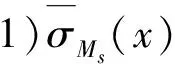
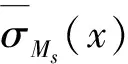
2 基于B样条神经网络算子的多变量散乱数据插值

在本节中,我们构造一类多元神经网络插值算子,对定义在R上的多元连续函数,建立一致逼近定理并且估计逼近误差。为了方便起见本文假设hX=qX。

假设X是散乱数据集,将X分解成嵌套的子集X1⊂X2⊂…⊂XM=X。Xk是X的子集。其中

其中xi=[-1,1]2,i=1,2,…,d,1≤λ<2,T=μ(s+1)。

接下来,构造多变量神经网络插值算子。首先,定义多变量域R:

R:=[-1,1]2×…×[-1,1]2。

(6)

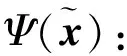
(7)

定义2.1假设f:R→R是一个连续函数，则多变量神经网络插值算子为:

(8)

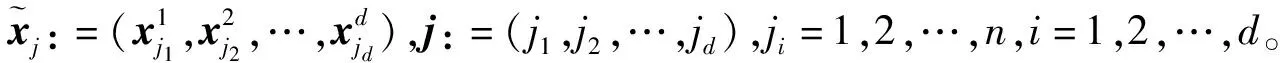
易见

(9)

(10)

(11)

定理2.1假设f:R→R是一个连续函数,则

证明如果固定任一个点k:=(k1,k2,…,kd),ki=1,2,…,n,i=1,2,…,d。则对索引集j=(j1,j2,…,jd),ji=1,2,…,n,i=1,…,d,如果k≠j,则km≠jm,m=1,…,d。

由假设hX=qX,有

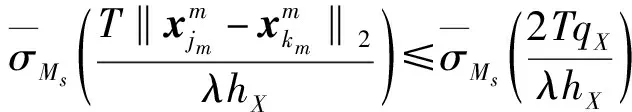
下面我们记

其中i=1,…,m,…,d。

故有

(12)

如果k=j,有

综上,

(13)

所以由(13)式,有

对于每j:=(j1,j2,…,jd),ji=1,2,…,n,i=1,2,…,d都成立。

定理2.1证毕。

在继续之前,我们回顾一下多变量函数的光滑模。假设f:R→R,记C(R)为R上的所有连续函数的集合,赋予通常的范数。对于任意f∈C(R),多变量函数的光滑模定义为

其中δ>0,‖·‖2表示R上的欧几里得范数。此外,对于连续函数f:R→R,有

=‖f‖∞<+∞。

(14)

定理2.2假设f∈C(R),则

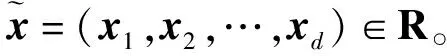
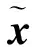
下面定义集合

和

则以上不等式可改写为

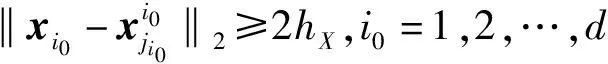
(15)

接下来,估计Δ1。

首先,定义‖·‖∞为R上的最大范数。即有

所以,对于索引集j∈S1,我们有

此外,在空间域R中有以下不等式成立

故,对于每一个s∈N+,结合‖Ψ‖∞≤1,

又由于,集合S1包含至少2d个元素。最后,得到

(16)

定理2.2证毕。

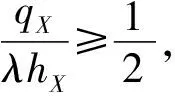
推论2.1假f(·)∈LipMα(0<α≤1),则

3 数值实验仿真与分析

本文的实验环境是Intel(R)Core(TM)i5-4590 CPU @ 3.30GHz处理器,在内存为4GB的计算机、MATLAB版本是R2016a上运行。

首先,我们给出的是1 000个散乱点在[-1,1]2上的均匀分布图。如图1。

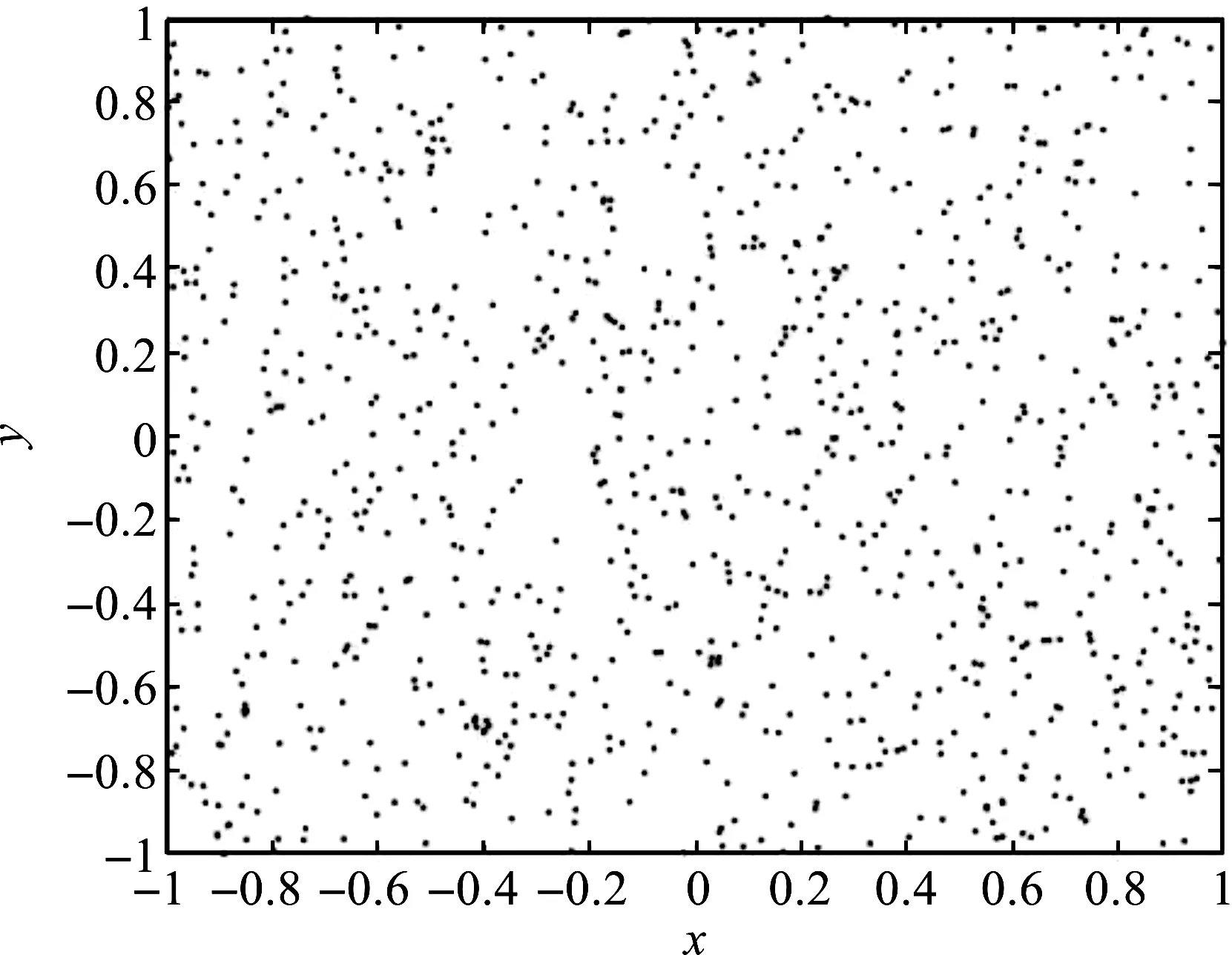
图1 1 000个均匀分布的散乱点

由于文中的非负Sigmoid函数σMs(x)是由s阶的B样条函数变化而来的。在本节中,我们将考虑由一阶B样条函数和二阶B样条函数(即s=1,2)变化出的两个具体的Sigmoid函数,即函数σM1(x)和σM2(x)来验证上文中给出的逼近定理。σM1(x)和σM2(x)定义为

(17)

及

(18)

例3.1考虑连续函数f1(x1,x2):[-1,1]2→R,定义为

例3.2考虑连续函数f2(x1,x2):[-1,1]2→R,定义为

f2(x1,x2):=sin(π·x1)×cos(π·x2)。

下面给出目标连续函数f1(x1,x2)和f2(x1,x2)的曲面图。如图2。

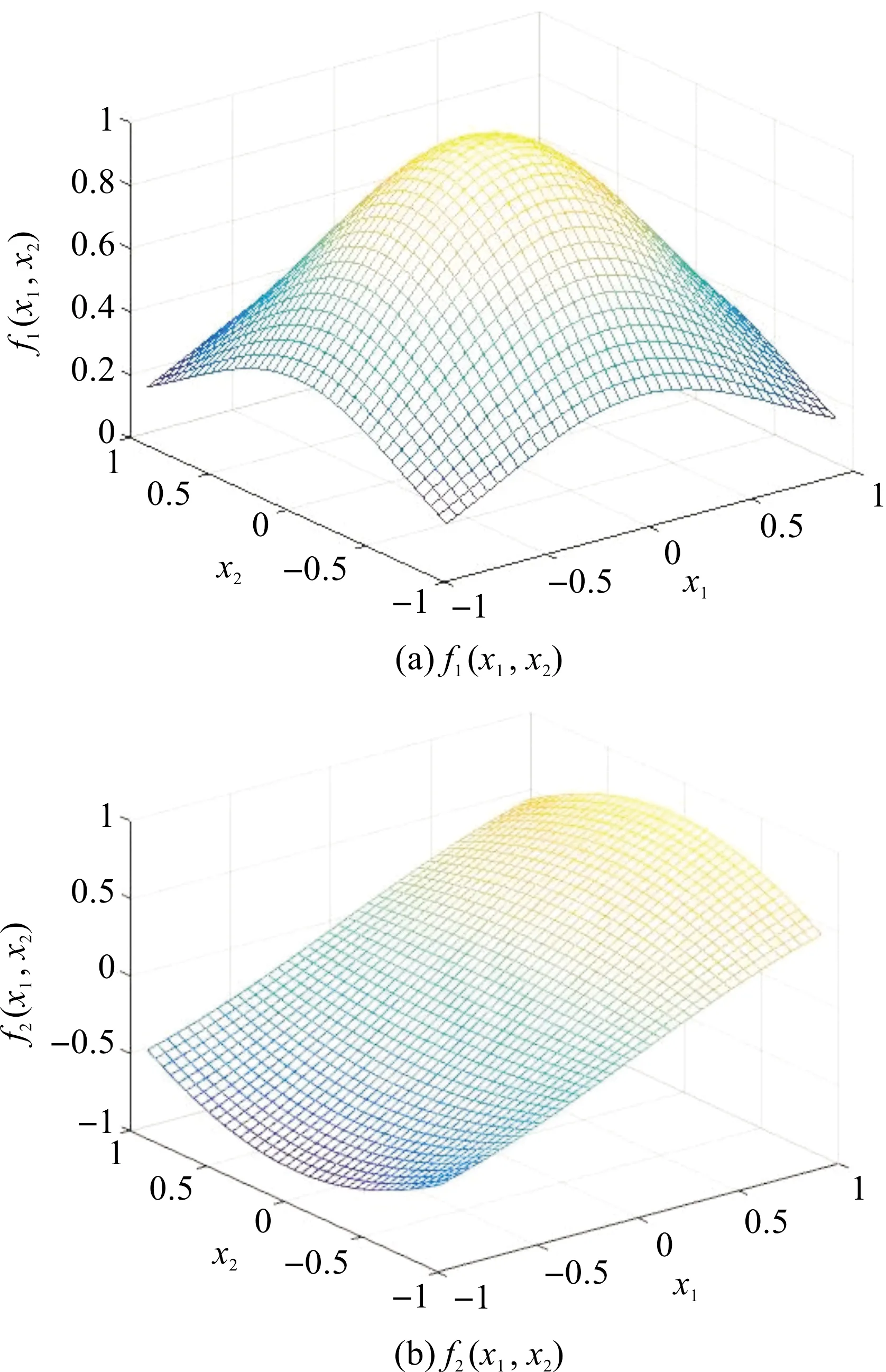
图2 目标函数曲面图

下面,针对以上两个曲面和定义的函数σM1(x)和σM2(x)。我们依次选取不同个数的散乱点来进行插值逼近,插值逼近的误差结果分别见图3和图4。

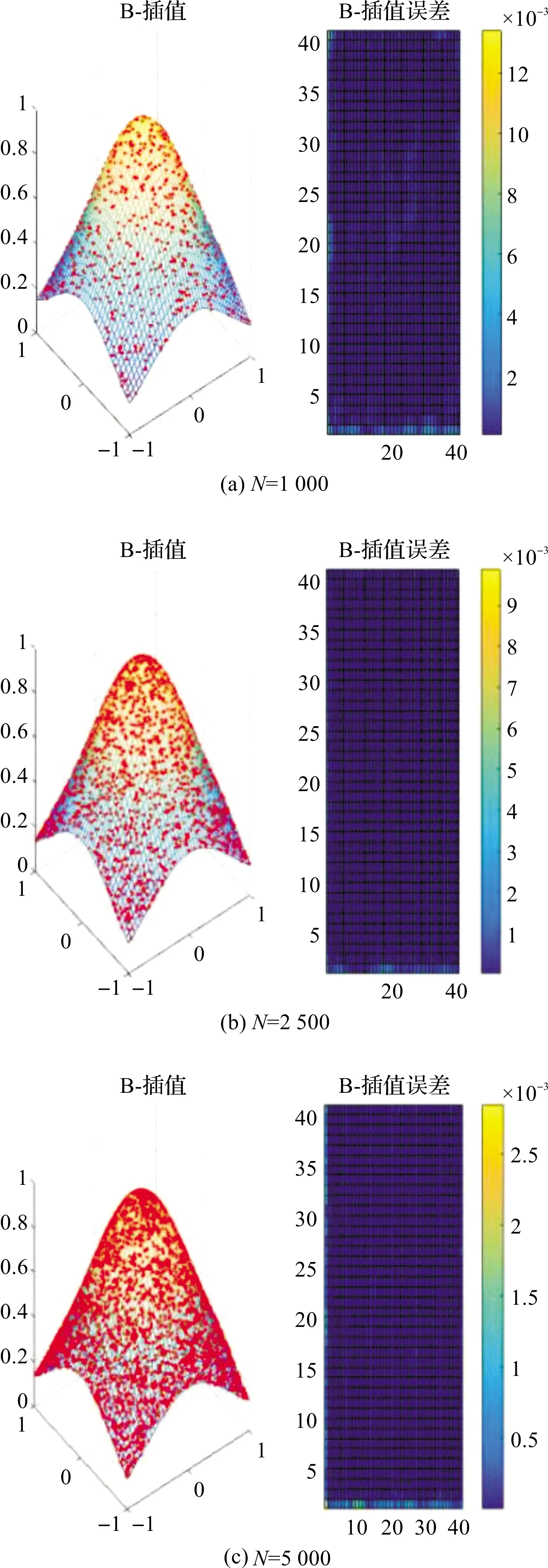
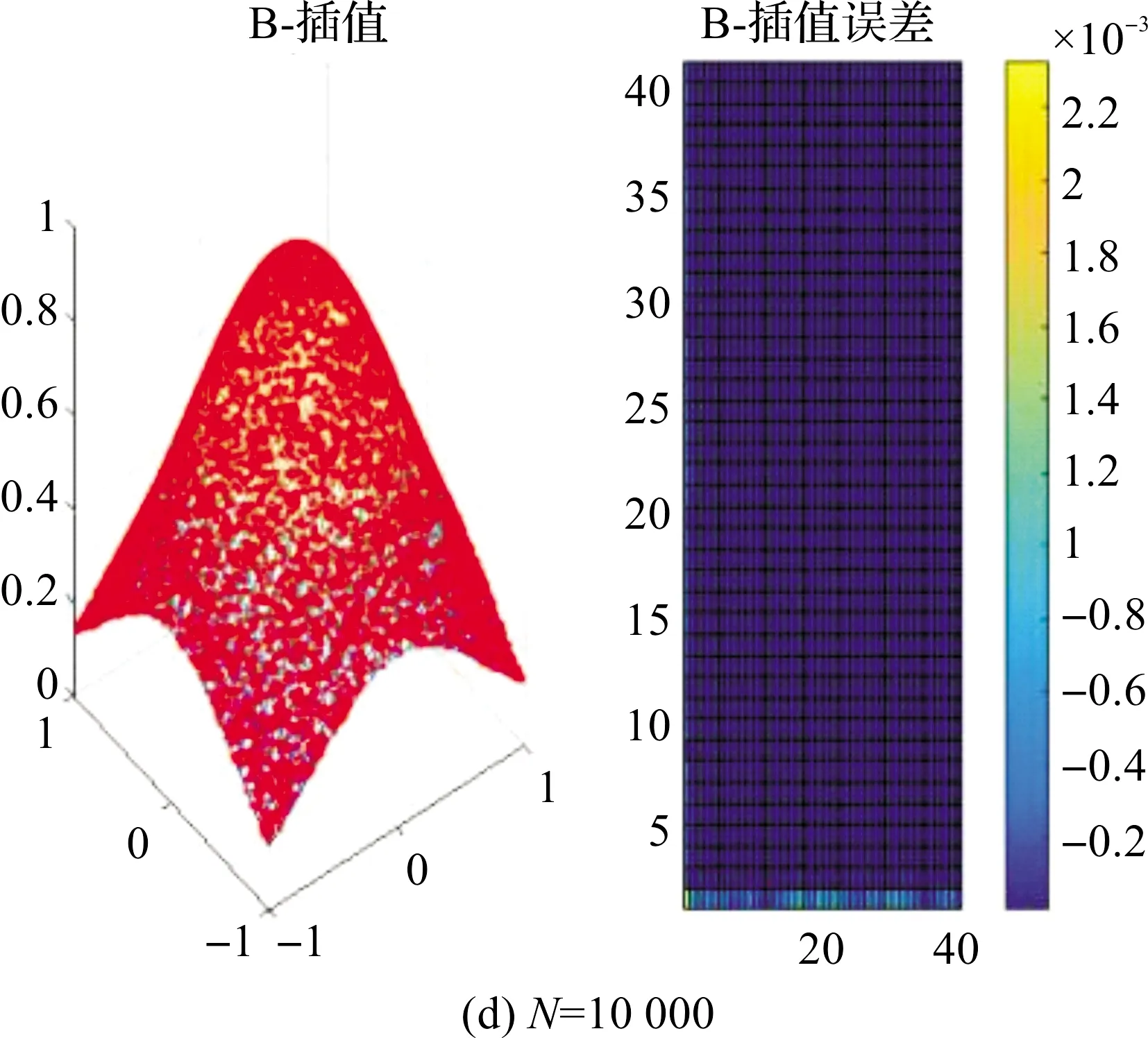
图3 s=1时,f1(x1,x2)的逼近效果

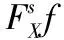
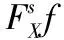
4 结 论

文章利用一维B样条函数构造了一类多元神经网络插值算子，研究了散乱数据的插值与逼近问题。对于定义在有界域上的多元连续函数建立了一致逼近定理，并且给出了逼近误差估计。通过对具体例子的数值模拟进一步验证了理论结果的正确性。