异质集成学习器在鸢尾花卉分类中的应用
2019-02-14史双睿
史双睿
(北京师范大学第二附属中学,北京,100088)
1 概述
分类模型的研究在机器学习中具有重要的意义。而集成学习作为提高分类模型性能的方法也广泛被使用。集成学习又分为同质集成学习与异质集成学习,目前在机器学习界,大多数采用同质集成学习,包括一些主流的机器学习框架,如sklearn,都只实现了同质集成学习。因此,对于异质集成学习进行探索就有了重要意义。
本研究依据具体的Iris鸢尾花卉识别实例,探究异质集成学习的方法。
■1.1 数据集特征
Iris是机器学习中一个常见的数据集,其用于鸢尾花卉分类,数据集共包含150个样本,每个样本包括花瓣长度,花瓣宽度,花萼长度,花萼宽度四个特征,样本共具有三个花卉类别,分别为Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),以及Iris Virginica(维吉尼亚鸢尾)。本研究将根据该数据集,探究异质集成学习的方法。
■1.2 数据集预处理
Iris数据集的预处理一共包含两个步骤:
(1)特征编码:第一个步骤需要将Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),以及Iris Virginica(维吉尼亚鸢尾)这三种类别的花卉映射成0,1,2 三个类别数字,映射后的数据才能参与模型的训练。
(2)shuラe处理:由于Iris数据集的前100个数据只包含0,1 两个类别的花卉,后50个数据全部为第2个类别的花卉。所以我们需要对着150个数据进行随机打乱后才能进行训练。
■1.3 数据集划分
为了模型的训练与模型的性能检验,我们需要把数据集分为训练集和测试集两部分。对于Iris数据集,一共具有150个样本。我们随机挑选出100个数据作为训练集,用于训练模型。剩下50个数据作为测试集,用于检验训练出的模型的性能好坏。
2 构建分类模型
■2.1 构建kNN模型
2.1.1 基本原理
kNN分类算法是一种临近算法,也是分类技术中最简单的方法之一。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。在训练阶段,模型通过将所有训练集映射在一个特征空间内。在预测阶段,模型将所有待分类的样本,通过计算与训练集的距离,挑选出最近的k个距离,在这k个训练集样本中,通过简单的投票原则,来决定待分类样本的预测类别。
2.1.2 在Iris数据集上应用kNN模型
在我们的Iris数据集上,我们通过将训练集的100个样本映射在一个四维特征空间内来实现kNN模型的训练。在预测过程,我们计算测试集的50个样本与训练集的100个样本的距离,从中挑选出最近的k个距离,然后采用投票原则来确定测试集样本的花卉种类。
2.1.3 结果分析
我们通过sklearn中的kNN模型包,在Iris数据集上运用了kNN模型。通过改变不同的k取值,观察在测试集上的准确率。经过测试,当k = 2,3,4,5时,模型在测试集上的准确率分别为86%,92%,88%,92%。当k = 3或5时,在测试集上的准确率达到最高92%。
2.1.4 kNN模型的优缺点分析
kNN模型的优点在于模型比较简单,结果也比较直观。但是缺点是当训练集样本非常大时,由于要计算每个测试集样本与整个训练集的距离,所以速度会明显的降低。但是由于我们的样本数目只有150个,因此采用kNN模型一方面计算速度很快,另一方面在测试集上能够取得不错的性能。
■2.2 构建逻辑回归模型
2.2.1 基本原理
逻辑回归模型是机器学习中一种常见的分类模型,其主要运用在二分类中。在多分类问题中,可以运用ovr或者ovo等策略将多分类问题转化为多个二分类问题来使用逻辑回归。逻辑回归的基本原理是采用sigmoid函数来作为我们的预测函数。在我们的鸢尾花卉分类问题中,sigmoid函数的输出就是属于每一类花卉的概率,范围在[0,1]之间。逻辑回归在训练的过程中,通过不断的最小化交叉熵代价函数,来寻求一个合适的学习参数θ向量,来使模型在训练集上的误差相对较小,同时在训练的过程中,通过加入一定的正则化项,来缓解模型的过拟合。
由于本研究为三分类问题,要对逻辑回归进行调整。这其中有两种方法:
(1)根据每个类别,都建立一个二分类器,带有这个类别的样本标记为1,带有其他类别的样本标记为0。假如我们有K个类别,最后我们就得到了K个针对不同标记、普通的逻辑回归分类器。
(2)修改损失函数,让其适应多分类问题。这个损失函数不再笼统地只考虑二分类非1即0的损失,而是具体考虑每个样本标记的损失。
2.2.2 假设函数
逻辑回归采用sigmoid作为假设函数,如式1所示。假设函数的值域为[0,1],对应了事件发生的概率。其中z =θTxX,θ是模型需要学习的参数,X在该问题中对应每个花卉样本的特征向量。即z是每个花卉样本所有特征的线性组合。

2.2.3 交叉熵代价函数
为了衡量模型的性能,需要在训练的过程中引入代价函数。对于机器学习中的分类问题而言,最常用的代价函数是交叉熵代价函数,如式2所示。其中yi为样本的真实分布,g(θ)为模型给出的预测值,即预测属于每一种花卉的概率值。模型在训练的过程中通过梯度下降法,不断的调整θ的值,来使模型在训练集上的代价函数不断的降低,不断的对模型进行优化。

2.2.4 逻辑回归的正则化
在训练的过程中,代价函数会随着迭代次数的增加而不断的降低,最终稳定在一个比较小的值。代价函数越小,说明对训练集拟合的越好,但是会带来机器学习中一个常见的问题,即模型陷入过拟合。此时模型虽然能够很好的拟合训练集,但是对于未知数据的泛化能力会比较低,也就是说,模型在测试集上的准确率会比较低。
对于机器学习中出现的过拟合问题,不存在一种手段能够完全解决。只从在一定程度上缓解。缓解过拟合的常用手段有两种。一种是增加训练集样本的数量,当训练集样本的数量增加时,模型可在一定程度上缓解过拟合,但是通常在实际情况下,我们很难去获取到更多的样本,或者说是获取更多样本的成本太高。所以我们一般采用第二种手段,即正则化,来缓解模型的过拟合。
正则化的基本思想是通过在代价函数的基础上,对学习到的参数向量进行一定的限制,使学习到的参数向量不会很大,从而能得到一个相对比较简单的机器学习模型,提高了模型的泛化能力。
常用的正则化手段有L1正则化和L2正则化,L1正则化是在代价函数的基础上,对学习参数进行L1范数限制,L2正则化则是对学习参数进行L2范数限制。L1正则化相对于L2正则化更容易产生稀疏解,偏向于得到一个更简单的模型。
2.2.5 在Iris数据集上应用逻辑回归模型
在我们的Iris鸢尾花分类问题中,由于花卉种类一共有三类。因此我们无法直接应用逻辑回归。但是我们可以采用ovr手段,将一个三分类问题转化为三个二分类问题。也就是分别把每种花卉作为一类,把剩下的两种花卉作为另外一类。在这种划分下,在每两个类别之间训练一个二分类器,也就得到了相应的三个判别函数。在预测阶段,我们将未知类别的花卉特征分别代入三个分类器中,然后取最大概率分类器的类别,作为未知花卉的类别。
同时,在训练的过程中,我们加入了L2正则化项,来缓解模型的过拟合问题。加入了正则化项的代价函数,如3式所示。
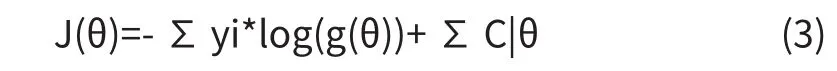
2.2.6 结果分析在经过若干时间的训练后,模型最终在测试集上达到了80%的准确率,这个准确率相对于KNN模型来讲,性能相差很大。其主要原因在于一般逻辑回归模型通常适用于二分类,在我们采用ovr手段把三分类问题转换为多个二分类问题的同时,会引入机器学习中另外一个比较常见的“偏斜类”
问题,即不同类别的样本数目相差比较大,会使训练出的模型性能不是很好。
■2.3 构建SVM模型
2.3.1 SVM模型基本原理
支持向量机(support vector machine,SVM),它最初于20世纪90年代由Vapnik提出,是机器学习中一种十分强大的分类模型。与数据挖掘中的其他分类模型相比,具有较好的泛化能力。而且针对非线性可分数据,拥有一套先进的理论方法来处理。由于其优秀的分类性能,在机器学习领域成为了研究的热点。在学术界,不断的有新的理论被提出。近年来,与SVM相关的方法,在人脸识别,手写识别,文本分类中得到了广泛的应用,并且取得了很好的效果[1]。
SVM可以简单的理解为是对逻辑回归模型的改进,对于逻辑回归来讲,是寻找一个超平面,把两类数据在特征空间中划分开来,对于线性可分的数据集来讲,可能存在无数个超平面将数据划分开来,而逻辑回归只是寻找到其中的某一个超平面。而对于SVM来讲,则是在这众多超平面中,寻找到最优的一个超平面,这里的是最优是指到两类样本点的间隔都相对较大。这个最优的分隔超平面可以使模型的泛化能力更强。
2.3.2 核函数
简单来讲,核函数的作用即为将数据从低维空间映射到高维空间。 因为在低维空间线性不可分的数据,在高维空间很可能是线性可分的,此时再运用SVM即可实现最优划分。实际应用中,可以利用参数来限制维度,以减小计算量。
在实际的数据集中,最常见的还是线性不可分的数据集,此时SVM无法直接使用,需要引入带核函数的SVM。核函数的作用主要是将在低维特征空间中线性不可分的数据映射到高维特征空间中,在高纬空间中,原本线性不可分的数据就有可能成为线性可分的数据。
2.3.3 结果分析
我们最终在Iris花卉数据集上尝试使用不同的核函数,如线性核函数,高斯核函数,多项式核函数等。在经过多轮迭代之后,最终在测试集上得到了92%的准确率。由此可见,SVM是泛化能力比较强的一种分类模型。
■2.4 构建集成学习器
2.4.1 集成学习基本原理
在人工智能的有监督学习中,我们希望学习到一个稳定的强大的强学习器,但是实际情况往往不那么理想,我们可能会得到若干个在不同的方面存在着不同缺陷的弱学习器。而集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型,集成学习的思想就是综合多个弱监督模型的优点,根据多个弱监督模型的决策结果来得到最终的决策结果。这样即使某一个弱分类器得到了错误的预测,那么其他的分类器也能将错误纠正过来。
集成学习器分为两种。第一种就是所有的个体学习器都是一个种类的,即同质的。比如都是决策树个体学习器,神经网络个体学习器等。第二种是所有的个体学习器不全是一个种类的,即异质。目前来说,同质个体学习器的应用是最广泛的,一般常说的集成学习的方法都是指的同质个体学习器。而同质个体学习器使用最多的模型是CART决策树和神经网络。
因此,从集成学习的基本思想我们可以知道,集成学习一共分为两步。第一步是得到多个基本的学习器,第二步是采用一定的策略,把第一步得到的学习器结合起来,得到最终的学习器。
2.4.2 集成学习之个体学习器
在机器学习中通常有两种方式得到个体学习器,第一种方式是所有的个体学习器来自于同一个模型,即是同质学习器,例如都来自CART树,或者都来自神经网络。另外一种方式是所有的个体来自于不同的模型,即是异质的,比如个体学习器分别来自KNN,SVM,逻辑回归等。
目前在机器学习领域,一般都采用基于同质学习器的集成学习。我们所说的集成学习在默认情况下都是指同质集成学习器。对同质学习器的研究也比较多,对异质学习器的研究比较少。但异质学习器同样作为一种重要的集成学习策略,被广泛使用。
2.4.3 集成学习之结合法
2.4.3.1 平均法
对于机器学习中的回归问题,比较常用的方法是将若干个基本学习器的输出求平均值来得到最终分类器的输出。
比较常用的求平均值的方法有算法平均和加权平均。最简单的为算法平均,如4式所示。如果每个个体学习器有一个权重wi,则最终的预测如5式所示。其中H(x)为集成学习器的最终输出,hi(x)为每个个体学习器的输出,T为集成的个体学习器的个数。

2.4.3.2 投票法
对于分类问题,一般采用投票法进行决策。每个弱分类器给出自己的判别结果,然后将所有的结果进行综合得到最终决策。
最简单的投票法是相对多数投票法,也就是我们常说的少数服从多数,也就是T个弱学习器的对样本x的预测结果中,数量最多的类别cici为最终的分类类别。如果不止一个类别获得最高票,则随机选择一个做最终类别。
稍微复杂的投票法是绝对多数投票法,也就是我们常说的要票过半数。在相对多数投票法的基础上,不光要求获得最高票,还要求票过半数。否则会拒绝预测。
更加复杂的是加权投票法,和加权平均法一样,每个弱学习器的分类票数要乘以一个权重,最终将各个类别的加权票数求和,最大的值对应的类别为最终类别。
2.4.4 在Iris花卉数据集上应用异质集成学习
在Iris花卉数据集上,我们采用了三个个体学习器,分别是KNN模型,逻辑回归模型,SVM模型,把这三个学习器采用基本投票策略的方式结合起来,票数最多的花卉类别作为预测样本的类别,最终得到了一个准确率更高更强大的学习器。
经过在测试集上进行测试,最终在测试集上达到了94%准确率,相对于单个个体学习器的最高只达到了92%而言,提升了2个百分点。这充分说明了在采用异质集成学习后,融合后的模型的性能得到了提升,取得了一定的效果。
3 结语
本文对Iris鸢尾花卉数据集,分别采用了单独的个体学习器KNN,逻辑回归,SVM以及异质集成学习,把单独的个体学习器在测试集地上的准确率从92%,80%,92%提升到了融合后的94%,充分说明了异质集成学习在该问题上取得了效果,也证明了异质集成学习和同质学习一样,具有广泛的应用前景。
