基于遗传算法—支持向量机模型的快速公交行程时间算法研究

熊 浩，韩 印 （上海理工大学 管理学院，上海 200093）

0 引言

随着生活水平的提高车辆数量的增加，拥堵已成为大城市出行亟待解决的问题，提出公交城市提高公共交通的利用率，促进公共交通，以解决大城市的交通拥堵问题。然而，低准时率的公共交通影响了人们对出行方式的选择。人工智能技术的进步，智慧城市理念的普及，使得人们对于公共交通到站时间预测采用智能化和自动化的方案。

现有的公交到港时间预测模型可以分为三类：交通流理论模型，时间序列分析模型和机器学习模型，根据它们的不同原理。交通流理论模型精度低，校准困难。卡尔曼滤波器模型具有较高的预测精度，较强的可操作性和在线预测，但对异常观测的抗干扰性较差。基于机器学习方法的预测模型具有较高的精度，神经网络模型具有良好的学习能力，能够很好地跟踪非线性，非平稳时间序列数据。但它需要大量的历史数据，并且存在诸如学习或学习不足以及局部最小化等问题。支持向量机是一种通过优化方法解决机器学习问题的新工具。近年来，它已被用于公交车行程时间预测，并且当数据样本很小且维数很高时，它仍然可以做出更好的预测。

综上所述，支持向量机模型能基于小数据样本，预测出较准确的到站时间。因此，本文旨在建立基于支持向量机理论的公交通行时间综合预测模型，并在此基础上，使用BRT数据作为数据库，在不同时间段实现BRT行程时间预测，并将预测结果与实际到达时间进行比较，以验证模型的准确性。分析了所提出的预测模型在不同时间段的适用性。

1 算法原理简介

将公交的行程时间分为相邻两站之间的运行时间和本站的驻站时间。

其中：ti+1为到达i+1站点的时间；ti为到达i站点的时间；si为在i站点驻站时间；Ti,i+1为车辆在i和i+1站点之间各段运行时间。

在路段运行时，运行时间受天气、路段、交叉口、发车时间、上下行等因素影响；在站台停留时，驻站时间受到车辆、客流量、站台形式、天气等因素影响。

1.1 支持向量机（SVM） 算法

SVM的主要思想是将训练数据集非线性地映射到高维特征空间（这个高维特征空间是希尔伯特空间）。此非线性映射的目的是在映射到高维特征空间之后将输入空间中的线性不可分数据集转换为线性可分离的数据集。然后创建分类超平面作为决策表面，以使正例和负例之间的隔离边最大化，是结构风险最小化的近似实现。它具有在各种功能集中构建功能的多功能性，不需要特定的功能形式，并且可以用于非线性系统，比如输出变量（如公交车行驶时间）和输入变量（如交通状况，客流要求等）之间的复杂关系。

SVM算法是具有线性约束的二次优化问题，结果是唯一且最优的。没有其他神经网络训练方法需要非线性优化，容易导致陷入局部最小值的风险。给定一组数据点 （x1,y1）、 （x2,y2）、 （x3,y3）、 （xk,yk），X表示输入向量空间，Y表示输出变量空间。SVM具有以下的函数形式：

其中：φ（x）是一种非线性映射函数，可以将输入向量空间X映射到高维特征空间H。

系数ω和b通过最小化规则化风险函数进行计算：

其中：第一项||ω||2称为正则化项，最小化||ω||2可使函数尽可能平滑，提高函数的泛化能力。第二项）称为经验风险函数，即通过测量不敏感损失函数得到的实验误差；常数C用于平衡结构风险与经验风险，通常C＞0。通过引入松弛变量ξi和并将上述问题转换为以下形式：

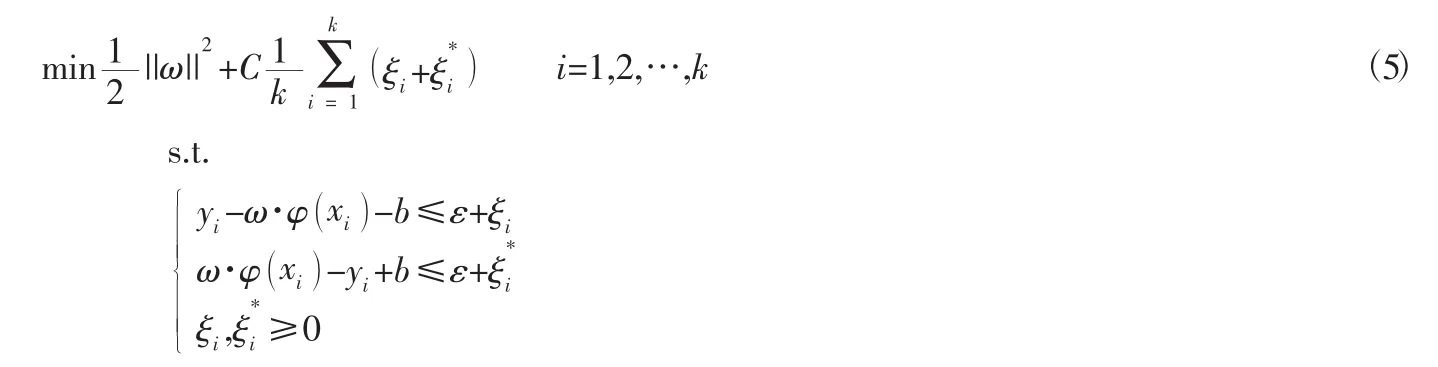
为了解决上述优化问题，引入拉格朗函数将上述形式转化为以下对偶问题：

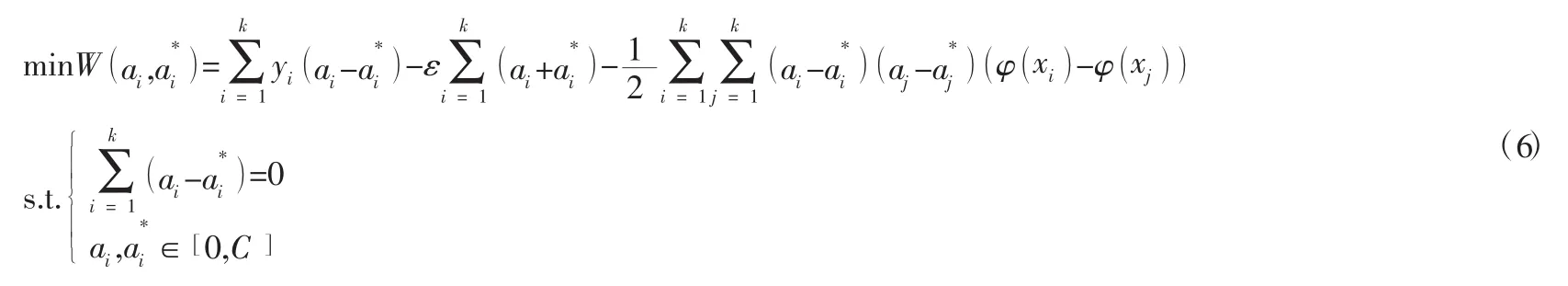
其中：ai和叫做拉格朗日因子。

则：

将核函数K（xi,xj）引入式 （7），得：

核函数K（xi,xj）为向量xi和xj在特征空间φ（xi）和φ（xj）上的内积。根据现有文献，本研究选择径向基核函数进行预测。径向基核函数如下：

为了获得结果最好的SVM模型，分别采用交叉验证、粒子群算法和遗传算法寻找参数C和γ的最优组合。

1.2 支持向量机（SVM）算法行程时间应用

影响公交车出行时间的因素非常复杂，包括天气状况、公交车运行时间、交叉口延误、路况、紧急情况等，这些都可能导致公交车行程时间的非线性变化。SVM模型具有很强的非线性预测能力，可以应用于模型预测。

因此在路段运行时，运行时间的影响因素包括天气、路段、交叉口、发车时间、发车站点、上下行。在站台停留时，驻站时间的影响因素包括车辆类型、客流量、站台形式、站台编号、天气、到站时间。

1.3 遗传算法优化原理

遗传算法（Genetic Algorithm，GA）最初是由美国Michigan大学Holland教授于1975年首次提出的，并出版了专著“自然与人工系统的适应”，遗传算法的名称逐渐为人所知，继承是生物的普遍特征，自生命诞生以来，它已经开始了漫长的进化过程。父母将遗传信息传递给后代，后代具有与父母相同或相似的特征；突变是遗传过程中亲本和后代之间性状的差异。它寻找基于自然进化规则的解决问题，例如适者生存，其特征不受搜索空间是连续还是略有不同的限制。它也适用于大规模并行计算，为传统数学方法难以解决或明显无效、复杂、非线性和优化的问题提供了一种新的有效方法。

遗传算法基于自然选择和生物遗传机制，用于全局优化，分类和评估其他数据挖掘技术的适用性。它通常包括3个基本操作，即父母选择、亲子交叉和子代变异。具体步骤如下：

（1）确定参数编码方案，并以二进制编码模式编码SVM相关参数。

（2）确定适应度函数，交叉验证模式中的准确率是遗传算法的适应度函数。

（3）遗传算法优化操作。

（4）遗传优化后，得到支持向量机的最优参数，最终得到最佳分类结果。

整个算法流程如图1：

1.4 模型参数

为了便于引入模型，之后要使用的主要模型参数符号如表1所示。

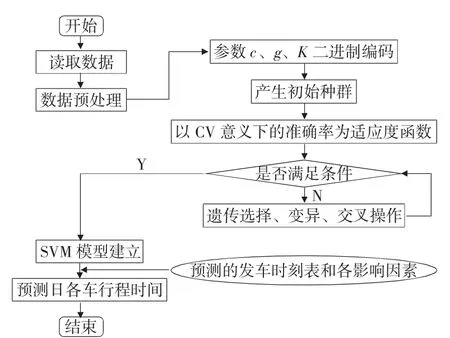
图1 遗传算法—SVM模型预测行程时间图

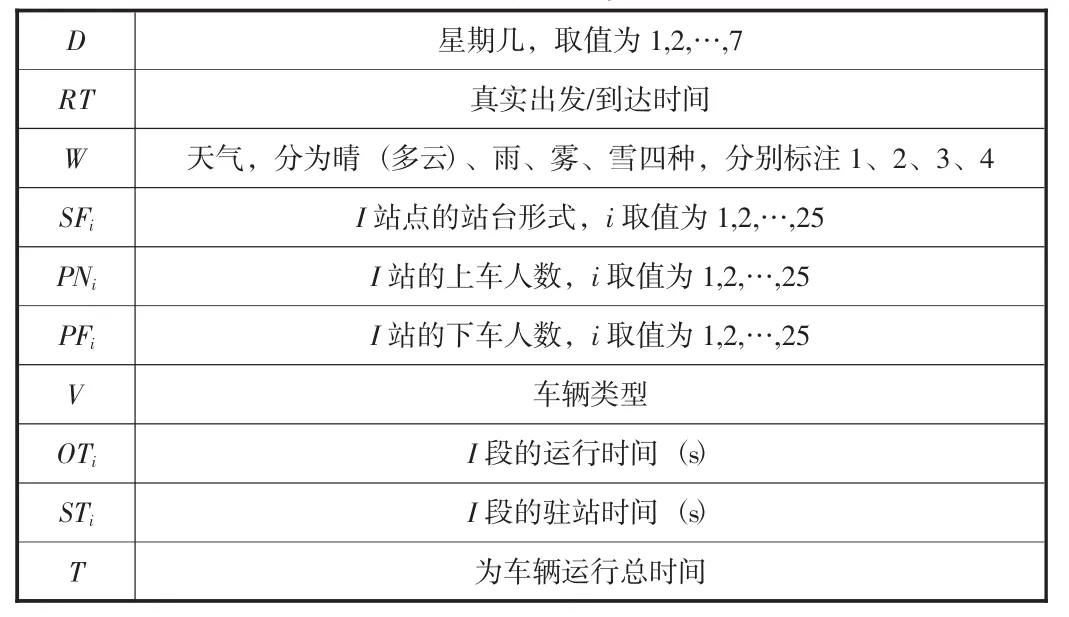
表1 符号和参数

2 数据处理

2.1 基础数据处理

为了验证模型的有效性，以上海市71路中运量公交线路为例对模型进行计算。71路中运量公交线路东起延安东路外滩，西至申昆路枢纽，共计25个站点，全长28.8km。该线路的公交车辆上面均装配有以GPS装置为主体的记录设备，该设备能够采集公交车的实时经纬度坐标、到站时刻、离站时刻、站点名称、站点编号、设备编号等信息，并将信息实时传输。每辆公交车的设备编号是唯一的，可用作匹配路段行程时间的标识。

数据是2017年11月21日到11月24日的上海市71路中运量公交各项数据。总共得到106 854条数据，经过分析，有效数据有91 863条。数据类型见表2和表3。

表2 BRT站间运行数据类型

表3 BRT驻站时间数据类型

上海市71路中运量线路及站点如图2所示：

2.2 数据分析

对处理后数据进行分析，7天的客流数据进行小时时间段分布，如图3所示，得出此线路公交车高峰运行时间在早上7:00～9:00和晚上5:00～7:00。在此基础上，对此线路运行站点客流进行分析，得出全天的客流呈现双驼峰，但早高峰刚性出行人数较多，所以短时上下车客流较多。

3 实验结果与分析

3.1 模型检验

本实验使用Matlab用于测试遗传算法优化模型的准确性。

3.1.1 评价指标确定

为了确定所研究的遗传算法优化参数的SVM模型预测结果的准确性，将前3天数据平均值和预测当天实际值作为比较加入，并且使用以下3个评估指标来评估预测结果：平均绝对误差（Mean Absolute Error，MAE），平均绝对误差百分比（Mean Absolute Percentage Error，MAPE） 和均方根误差（Root Mean Square Error，RMSE）。其计算公式见公式（10） 至公式（12）。

图2 上海市71路中运量线路及站点图

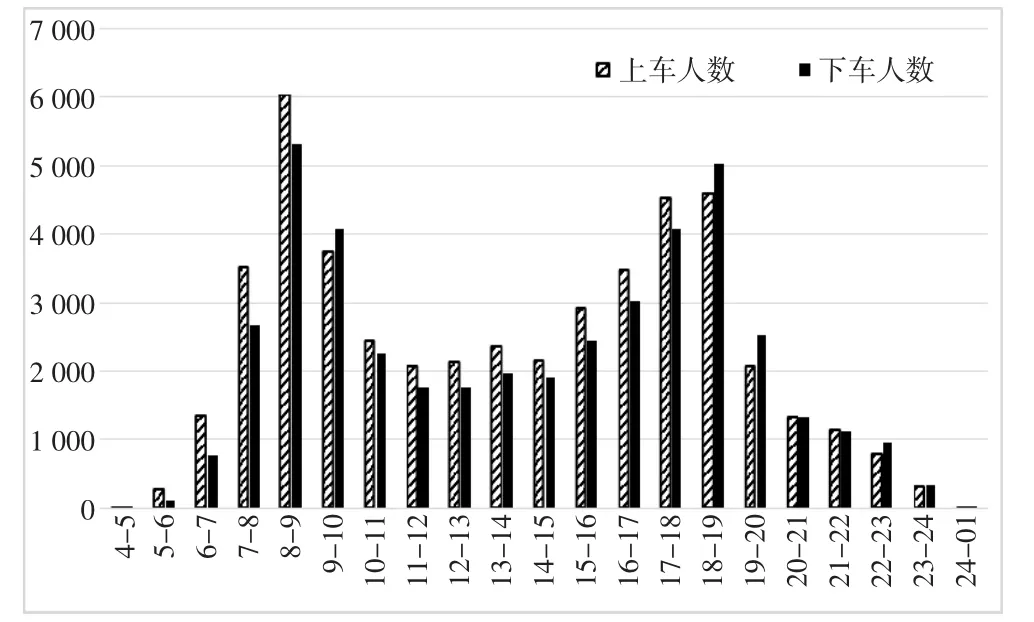
图3 上海市71路中运量上下客人数柱状图

其中，N为观测值、预测值对数。

3.1.2 结果对比

利用matlab对数据进行预测，将其预测结果与实际结果进行对比。由表4可以看到，GA预测出的数据虽跟实际值有8%～10%左右的误差，但相比使用前3天的平均值得出的结果，GA预测更加精准。

GA-SVM预测出的驻站时间偏差相比运行时间稍大，这是因为71路大部分是专有路权，运行中所受干扰较普通公交小。

3.2 结果分析

图4显示了早高峰相邻每站时间的结果对比。在GA-SVM模型和平均值对比下，GA-SVM算出的每站时间趋势与实际值更加相近，且偏差不大。但平均数趋势不甚明显，可能是由于平均数综合了全天的数据，本次只是早高峰的数据。

图5更是验证了之前的结果。图5在前5站由于人少、交通干扰少，两种算法的行程时间值和实际值偏差不大。但到达第6站之后进入市区，平均值出现大幅偏差，而GA-SVM的值趋势仍趋近真实值，但由于模型学习了3天的全天数据，本次实验只针对早高峰，导致部分时间预测出现偏差较大。

图4 相邻每站时间预测结果对比

图5 行程时间预测结果对比

4 结束语

本文预测了上海中运量车的到达时间，并将到达时间分为车站间的运行时间和车站的驻站时间。根据天气、时间、公交车类型和平台类型等影响因素，建立支持向量机回归预测模型，并通过matlab验证模型的准确性。通过数据分析，讨论了3天到达时间数据对后一天到达时间预测的影响，为决策者更好地选择公交到达时间预测模型提供了指导。研究结果表明：

（1）所建立的基于遗传算法参数寻优的支持向量机模型，经过数据学习后，能预测出较为准确的快速公交到站时间和行程时间。结果表明，遗传算法寻优参数更加准确。

表4 时间对比

（2）GA-SVM针对小批量数据的学习能预测出比较准确的驻站时间和运行时间。相比平均值法，得出的时间更加精准，更加适用。