基于XNN的库存需求预测

聂 敬，胡 卉，杨万里，刘庆凯

（长安大学 汽车学院，陕西 西安 710064）

0 引 言

一直以来，关于如何准确预测需求信息的变化，避免牛鞭效应的产生成为学术界研究的热点。简单来看，由于供应链串联递归效应的存在，使得其上各级库存、生产决策前，首先要预测下游市场需求的大小，然后再向上游发出满足自身的订单，由此，准确预测下游需求成为了减小提前期供应，避免缺货、断货和成本损失的关键。尽管随着供应链结构研究的深入，信息共享方式和先进库存管理方法的引入，在一定程度上可以提高需求预测的响应时间和订单处理速度，但由于现有需求预测方法的差异使得市场预测精度不高，导致现有库存不能满足市场需求的随机波动，造成很大的损失。王瑛（2004）基于核心制造企业的多级库存控制系统，提出了采用合作需求预测确定订购临界点，并建立了由供应网络、核心企业、分销网络组成的多级库存系统优化模型。李程（2013）使用灰色GM 1,（）1模型和BP神经网络变权组合预测得出组合预测值。孙志刚等（2013）采用蚁群算法优化支持向量机，并构建ACO—LSSVM物流需求模型。

相对于传统的预测方法，XNN具有良好的模式辩识能力和在任意精度内逼近非线性映射的能力，这意味着XNN能够自动地逼近那些最佳刻划样本数据规律的函数，不仅能很好地估计非线性函数，而且能处理数据中去掉线性部分后残差的非线性，通过使用一个或多个隐含层，网络能够自动分割样本空间，并在不同的子空间里建立不同的函数。

1 基于加性索引的可解释神经网络

XNN基于加性索引模型的概念，如下所示：

左侧的函数可以表示为K个平滑函数gi（·）的和。这些平滑函数（即岭函数）都用于在网络中训练的输入特征的线性组合（βiTx）。可解释神经网络提供加性索引模型的替代公式作为结构化神经网络。XNN内置了解释机制，这有助于解释和理解模型内部过程以及该模型学到的函数。

替代公式如下：

位移参数μ和尺度参数γk被用于模型拟合，但不参与识别，它们帮助模型通过正则化选择适当数量的岭函数。

XNN结构中三个重要的组成部分包括：

（1） 投影层（第一个隐藏层）

输入层包含将输入神经网络的所有信息。输入层全连接到投影层，在投影层上传递特征（信息）。投影层由k个节点组成（每个节点对应一个岭函数）。第一个隐藏层中的节点i的权重对应相应岭函数输入的系数（βi）。

（2） 子网络（图1的中间部分）

子网络主要用于学习应用于输入特征的岭函数。岭函数对于子网络而言非常重要，因为它们逼近投影层的复杂函数。在模拟中，研究者发现，使用由具有非线性激活函数的两个隐藏层组成的子网络，足以在拟合模型时学习足够灵活的岭函数。

（3） 组合层（最后的隐藏层）

组合层是XNN的最后一个隐藏层，由单个节点组成。节点的输入包括岭函数的所有输出以及在子网络中学习和添加的权重。在该层上使用线性激活函数，因此整个网络的输出是所有岭函数的加权和的线性组合。

2XNN模型构建

XNN类似于BP神经网络，是一种“前馈神经网络”。如图2所示，在前向传递过程中，当网络接受到一种学习模式后，神经元的激活值经输入层到隐藏层逐层经过加权求和及激活函数的变换，直至输出层。如果输出层得不到期望输出，则转入误差信号反向传播，将误差信息按照输出层输入向输入层方向逐层传播，根据预测误差的梯度值调整各层网络权值和阈值，最后回到输入层。

图1 XNN网络结构

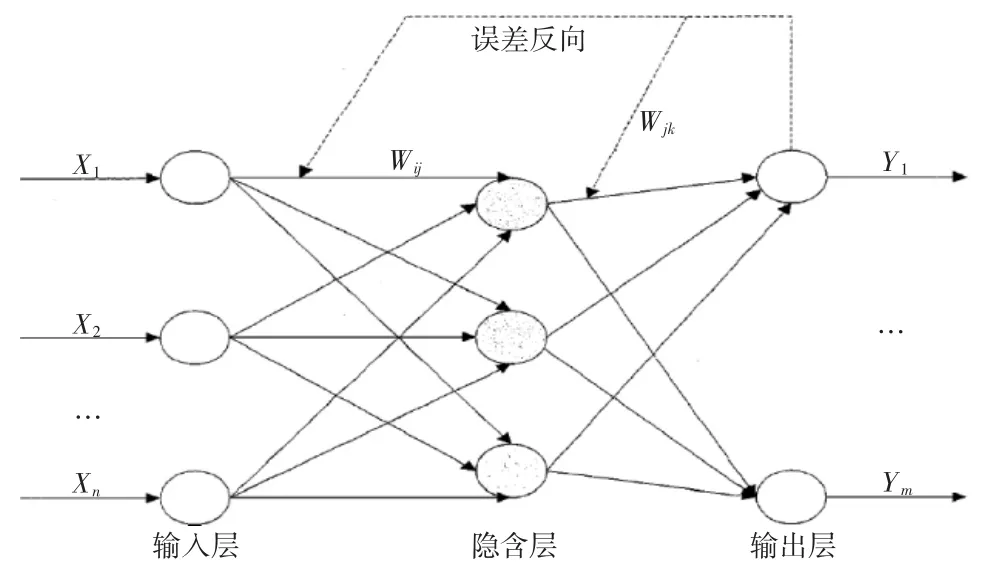
图2 神经网络结构图

图2中，X1,X2,X3,…,Xn是神经网络的输入值，Y1,Y2,Y3,…,Ym是神经网络的预测值，Wij和Wjk为网络连接权值。从图2中可以看出，神经网络可以看成一个非线性函数，影响库存需求的相关因素为网络输入值，输出为库存需求的预测值，输入值和预测值可以分别当做该函数的自变量和因变量。当网络输入节点数为n、输出节点数为m时，BP神经网络就表达了从n个自变量到m个因变量的函数映射关系。

在BP网络中隐含层的神经元的输出为：

式子中yi是第i个神经元的输出信号，f是传递函数，Wij是第j个输入信号和第i个输出信号之间的权值，θi为阈值。网络隐藏层有多种表达形式，通常选用Sigmoid函数：

2.1 预测步骤

神经网络在学习过程中，采用的是误差反向传播法，针对供应链库存需求预测，其一般步骤为：

（1）初步确定网络结构，选择样本相关数据。根据库存需求的特点，以及最终库存需求的确定，以管理者的视角，其库存需求预测的相关因素如图3所示：

如图3所示，网络有1个输出，6个输入。输出为库存需求预测，输入为初始需求、订单量、现有库存、需求增长、销售值和节点等级。

为方便计算，将输入与输出因素量化，用库存单位s表示库存基数，库存总需求为S，各个不同的输入因素量化结果如表1所示：

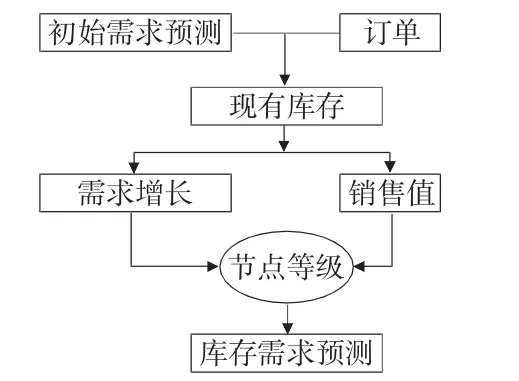
图3 库存需求预测主要影响因素

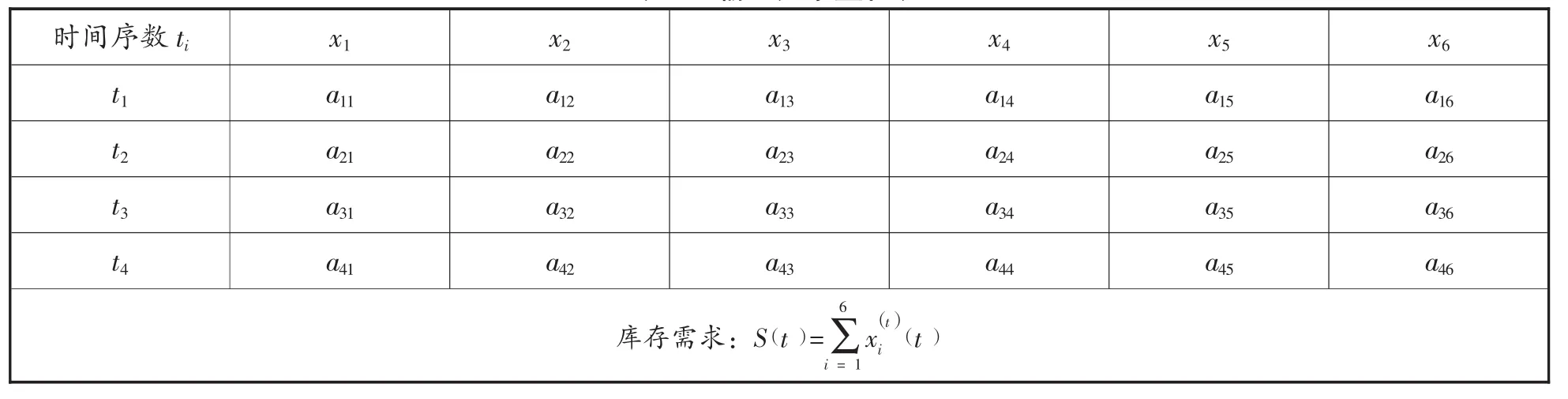
表1 输入元素量化表

S1,S2,…,S6分别代表初始需求、订单量、现有库存、需求增长、销售值和节点等级。t1,t2,…,t4分别代表供应链生命周期中的导入期、生长期、成熟期和衰退期，函数x（t）表示在时间为t时，该输入元素持有的库存量，φi为影响因素与库存基数的正比例系数。

（2）设定初始权值及其他有关参数。设定学习效率η和误差控制变量ε并训练网络，对给定的训练模式，计算网络的输出及其误差E，若E<ε，则学习结束；否则执行下一步。

隐藏层神经元的输出为：

输出层各个神经元的输出为：

权值的更新：

误差计算：

阈值更新：

以上式子中Hj代表隐藏层节点输出函数，Ok代表输出层各个神经元的输出，ek表示输出层k点的误差，bk表示输出节点的阈值，aj表示隐藏层节点的阈值。

（3）修正相应的权重，按照δ学习规则修正权重和阈值，然后返回上一步继续。

2.2 模型构建及其求解

本案例输入数据为6维，输出数据为1维，得到神经网络为1-1-7-1，即A层有1个节点，输入为时间t；B层有1个节点；C层第1到6分别输入初始需求、订单量、现有库存、需求增长、销售值和节点等级6个经过归一化后的数据，输出为库存需求预测量。

设定：神经网络的学习率为η=0.25，势态因子为α=0.73，对学习率作如下调整：

式（15）的解释是，如果连续两次迭代其梯度方向相同（sngo为符号判断函数），说明收敛速度较慢，则η学习率加倍；如果连续两次迭代其梯度方向相反，说明迭代过了头，则学习率η减半，也就是说误差代价函数在不同的方向按照各自比较合理的步长向极小点逼近，实现整个网络学习过程中步长自适应调整。

3 隐藏层的解释

通过对模型求解，将XNN的加性索引正则化，模拟了5个自变量，即x1,x2,…,x5，X服从［0,1 ］之间的均匀分布，x4,x5降为噪音变量，只针对第一层投影层和输出层惩罚强度进行调整y=f1（x）+f2（x）+f3（x）+f4（x）+f5（x）构建成为一个具有5个子网络的XNN模型，构造3个勒让德多项式来拟合x1,x2,x3分别为（如图4所示）：

图4 前3个勒让德多项式

图5显示了岭函数，第i行表示子网络i，第一列表示解释了单变量函数，其中包含由子网络学习到达其输出的权重。第二列显示βi的值，即投影系数。投影系数说明输入特征的哪个组合在通过子网络之前用作了每个岭函数的输入。在上面的例子中，从XNN的结构我们可以看出Subnetwork1已经学习了立方勒让德函数 （f3（· ）），Subnetwork2已经学习了二次函数 （f2（· ）），并且只有x2的系数非零。

4 总结

可解释神经网络（XNN）是一个关键的机器学习模型。与其他机器学习模型不同，它能「打开」神经网络的黑箱。该模型的结构和设计方式使其可以解释学习的特征以及导致其输出或预测值的函数。这些可解释性特征非常吸引人，它本质上是有可加性的，并且能通过纳入神经网络的机制（如子网络）直接得到解释。无论将XNN用作主要模型还是用于更复杂模型的替代模型，XNN都可以直接解释模型如何使用输入特征进行预测。这项技术为将机器学习模型整合入众多不同行业提供了巨大的优势，因为它能够超越现有系统，并且能够清晰解释它如何获得输出。

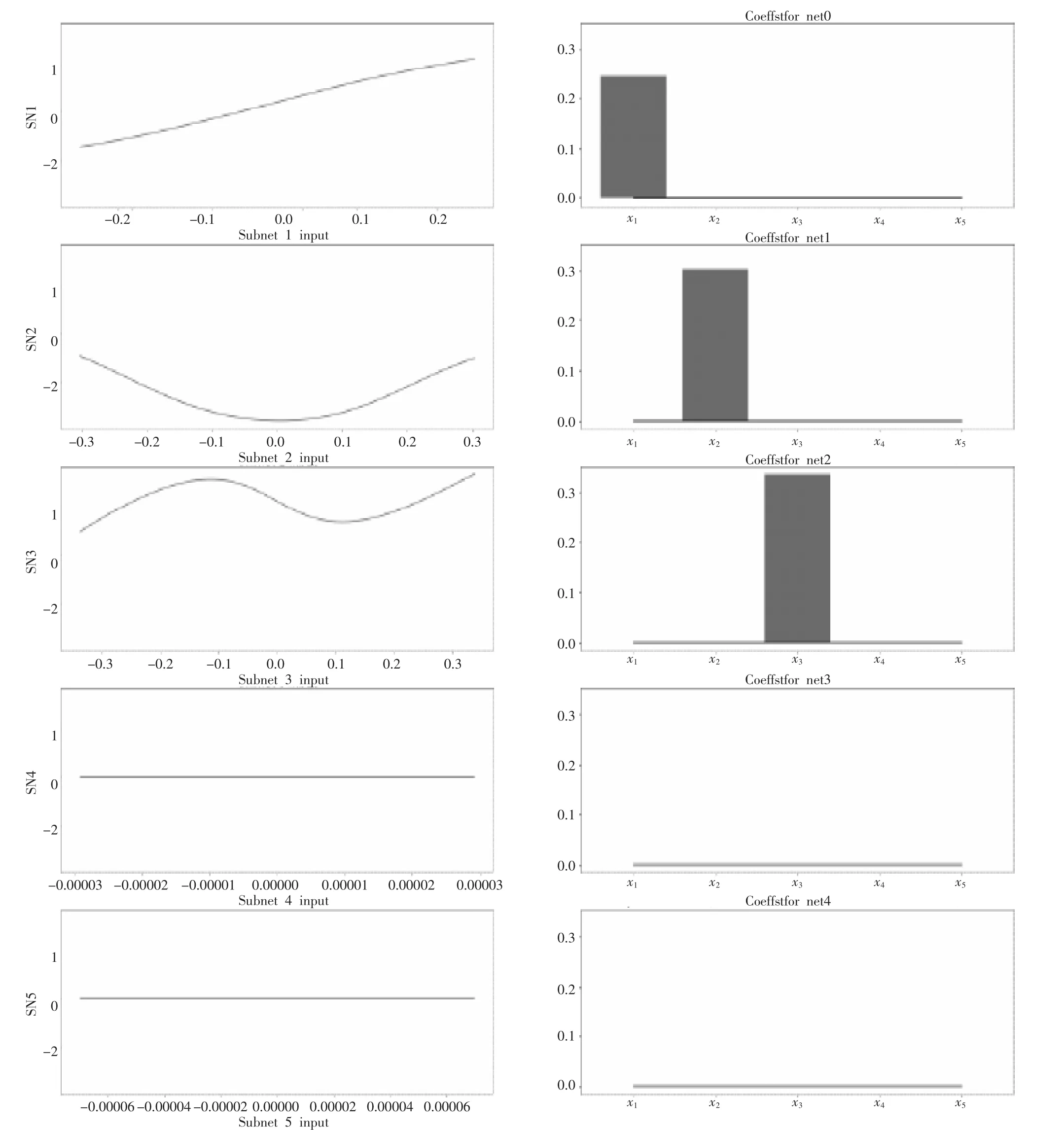
图5 训练后的岭函数（左）和对应的投影层指数（右）

[9] TANG W,LI W.Application of Support Vector Machines Based on Time Sequence in Logistics Forecasting[J].Logistics Management,2005(1):2.

[10] Freitas P S A,Rodrigues A J L.Model combination in neural-based forecasting[J].European Journal of Operational Research,2006,173(3):801-814.

[1l] Tsai T H,Lee C K,Wei C H.Neural network based temporal feature models for short-term railway passenger demand forecasting[J].Expert Systems with Applications,2009,36(2):3728-3736.

[12] Widiarta H,Viswanathan S,Piplani R.On the effectiveness of top-down strategy for forecasting autoregressive demands[J].Naval Research Logistics（NRL）,2007,54(2):176-188.