基于高斯-拉普拉斯金字塔的DR图像增强改进算法研究

【作 者】朱 伟，刘 健，竺明月，邵 勤，严 郁

1 南京中医药大学附属医院（江苏省中医院），南京市，210029

2 南京医科大学生物医学工程系，南京市，210029

0 引言

图像增强技术是对图像中的某些特征进行增强或抑制，提高感兴趣区的对比度，从而达到改善图像视觉效果的目的。对于医学DR（Digital Radiography）图像而言，由于噪声或其他原因使图像对比度降低、边缘模糊，尤其是胸部、盆腔和脊椎等纹理信息较多的部位，需要更高的图像对比度才有利于医生诊断，因此需要研究DR图像增强[1]。传统单一尺度增强技术，如直方图均衡、边缘增强等代表两种不同思路的增强算法，均对提高图像对比度有较好效果，但无法做到既能突出细节边缘又能凸现层次感，且增强图像的同时会带来噪声，容易导致谷粒效应[2]。小波变换融合两种思路的优点，可较好地解决上述问题。高斯-拉普拉斯金字塔算法即基于小波分析的思想，在多尺度上进行图像分解、细节增强和图像重构，较单一尺度能更好地实现图像细节增强，是多尺度分析的经典算法[3]。金字塔算法对大分辨率的DR图像增强方面有极大优势，也是DR图像增强的重点研究算法[4]。既往对金字塔算法的研究主要集中在图像的细节增强方面，而没能很好地利用图像的低频分量，即影响人眼视觉系统的信息。此外，还未注意图像金字塔图像冗余信息对算法时间复杂度的影响[5]。本文在考虑人眼视觉特性及获得更好细节增强效果的前提下，对高斯-拉普拉斯金字塔算法提出了改进，根据实验结果对本文提出的算法进行分析及评价。

1 高斯-拉普拉斯金字塔算法阐述

高斯-拉普拉斯金字塔是最基本的图像塔，其基本原理是：以抽样率为2将图像分解为多尺度的金字塔图像序列，每次分解所得到的图像分辨率均下降为原来的1/2，因此每层图像大小变为前一层图像大小的1/4。然后将所有图像的金字塔在相应层上以一定的规则融合得到合成金字塔，再将该金字塔按照其形成的逆过程进行重构得到融合金字塔[6]。同其他多尺度增强算法一样，包括图像分解、高频细节增强、图像重构等三个步骤，如图1所示，具体阐述如下：

（1）图像分解，即高斯-拉普拉斯金字塔的建立。首先将原始输入图像作为最底层图像F0，与模板卷积进行低通滤波，然后以2为步长对卷积后的图像进行行和列的下采样，得到平滑图像F1并将其作为下一级的输入图像再进行卷积及下采样，反复迭代直至图像尺寸变为1×1(或达到指定的分解级数)， F0-FN共同构成了高斯金字塔[7]。本文定义高斯金字塔的第l层图像为Fl：

式中N为高斯金字塔最顶层，Rl和Cl分别为高斯金字塔第l层的行数和列数，W(m, n)是一个低通滤波卷积核，可根据需要选择不同尺寸的模板。

拉普拉斯金字塔反映的是高斯金字塔两级之间的信息差，即图像经过卷积及下采样操作时丢失的高频细节部分，也是DR图像诊断时最关心的部分[7]。高频细节部分可通过每层高斯金字塔图像与其上一层图像内插扩大后的差值图像Dl获得， D0-DN共同构成拉普拉斯金字塔，此过程相当于带通滤波。高斯金字塔的第l层图像Fl通过内插获得放大图像Fl+1，使Fl与Fl+1的尺寸相同，内插算子如下：

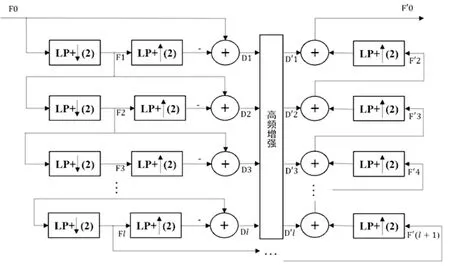
图1 高斯-拉普拉斯金字塔传统算法Fig.1 Gauss-Laplace pyramid traditional algorithm

（2）高频细节增强。图像经过分解后形成了高斯和拉普拉斯金字塔，其中拉普拉斯金字塔的各级图像代表着不同尺度的细节信息[8]。高频细节增强的目的是增强拉普拉斯金字塔的各级图像Dl，通常方法是通过非线性变换进行增强处理使其变成Dl'，在不失真的情况下改变原图细节信息的频率结构，使重构出的图像呈现出更丰富的细节。

（3）图像重构。图像的重构为图像分解的逆过程，从其顶层开始逐层从上至下按进行重建[8]。具体算法见式(4)：对最后一级分解得到的图像FN做内插，与上一级经过高频细节增强后的图像'，相加得到图像，然后将作为下一次重构的输入，逐级循环重建，直至得到和原始图像F0同样尺寸大小的输出图像。

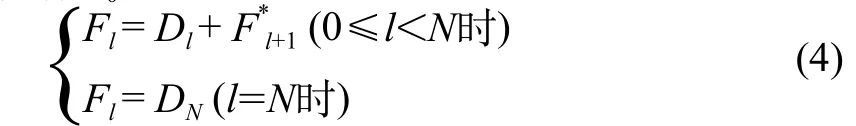
2 算法分析与改进

通过上述已知，高斯-拉普拉斯金字塔图像增强算法是通过多尺度的分解、高频细节增强、图像重构等步骤实现图像细节增强，其中对高频细节对比度增强是整个图像增强算法成败的关键，一般可通过突出细节边缘和凸显层次感两种方法来实现图像对比度的提高[9]。非线性变换不仅要保证重建图像不失真，而且要针对金字塔每一尺度图像特点给予不同的增强权重。不同的非线性变换的增强效果也不同，对于DR图像，为了获得更好的对比度增强效果，本文采用指数函数增强：

其中，x代表输入图像，y(x)代表输出图像，p控制曲线弯曲程度，不同参数p的增强效果差别很大，为了保证所有边缘均得到增强，且信号弱的边缘的增长幅度大于信号强的，则需p<1，这样可以使得DR图像在骨骼增强的同时软组织也清晰可见[10]。经过实验测试证明，在不增加噪声干扰的前提下，p取值范围在0.7～0.85之间能得到最好的细节增强效果。

增益系数a代表根据不同塔层预设不同的权重，对于图像边缘弱的增强，预设放大因子（a>1）；对于图像边缘强的抑制，预设压缩因子（a<1）。在图像分解过程中发现，一般在第四级是分水岭，前三级图像细节较小，第四级开始细节比较明显。因此，为使图像比较均衡，对前三级乘以较大的系数，对后面几级乘以较小的系数。综上，对第四级设置a=1，从第0级到最后一级逐级递减，渐变式系数可以使图像灰度变化剧烈区域的谷粒效应最小化。

金字塔算法是将图像分成不同的尺度进行处理，假设原始输入图像尺寸为N×N，对图像进行金字塔L级分解，每级分解后图像大小变为原来的1/4，第L级分解后各级图像的像素点总和为：

根据上式，显然分解后所有尺度像素点总和大于输入图像的像素点，因此在分解得到的金字塔图像中存在着大量冗余信息。尽管这种冗余对图像高频分量增强、去噪等方面有用，但会大大增加算法的时间复杂度[11-12]。对于分辨率在2 000×2 000或2 000×3 000级别DR图像，金字塔分解至少需要11级，计算量变得非常大，因此需要降低算法的时间复杂度。李名庆等[13]提出了在不影响图像整体质量前提下，通过去掉低通滤波来加速金字塔算法。但是去掉低通滤波会在下采样时丢掉部分信息导致重构图像失真，因此建议保留低通滤波。

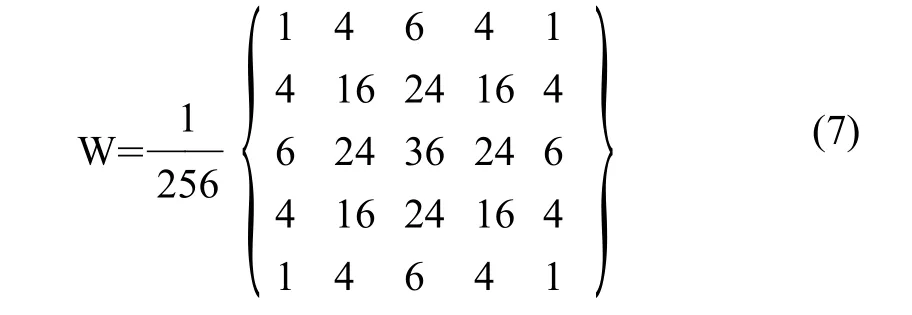
低通滤波的模板尺寸直接影响增强效果，在DR图像增强应用中，一般使用小模板增强肺部纹理等，使用较大模板增强骨骼等信息，如要增强背景信息则要使用更大的模板[14]。本文选用反锐化掩模算法中广泛使用的二维可分离的5×5的高斯核进行平滑，如式（7）。该模板有三个优势：①高斯核是唯一的线性核，即使用高斯核对图像模糊时不会引入其他噪声；②保证了经平滑后的高一层图像中的像素点与低一层图像中对应像素的相邻像素相关，避免下采样时直接丢掉部分信息导致失真；③减少冗余信息，降低了时间复杂度，同时也减少了存储空间[15]。

此外，通过对算法分析后还发现，金字塔算法只是针对每一尺度空间的拉普拉斯图像（高频分量）增强，而未能利用高斯图像，即低频部分，而该部分决定图像的全局亮度信息。人眼视觉系统是一个空域内的带通滤波器，图像亮度过高或过低情况下的图像增强对于辅助诊断没有任何实际意义[9]。因此在进行图像增强的同时应把握好图像亮度，使低频分量呈现均匀分布的状态，从而使图像整体效果符合人眼视觉系统。

综上，本文在基于人眼视觉特性及获得更好细节增强效果的基础上，对高斯-拉普拉斯金字塔算法提出了改进，对于低频分量采用直方图均衡使图像灰度显示更加均衡；对于高频分量采用指数函数增强，同时为使图像增强效果更好，根据不同塔层图像预设不同的增益权重。改进算法如图2所示，基本步骤如下：

（1）图像分解及细节增强

① 从第1级开始，输入尺寸为M×N的图像F0作为高斯金字塔第1级，对其进行5×5的高斯滤波，并对图像隔行隔列下采样得到F1，尺寸为M/2×N/2；

② 对F1进行5×5的高斯滤波，并将图像内插放大尺寸至M×N，得到E1，根据公式（5）对E1进行细节增强；

③ F0减去E1得到细节图像D1，尺寸为M×N；

④ 将步骤①采样的图像F1赋给第1步的F0，M变为M/2，N变为N/2，顺序执行①～③，直到F0图像尺寸为1×1。

（2）图像重构

① 从最后1级开始，最后1级(设为第l+1级)的金字塔图像F ' (l+1)，尺寸为a×b，将F' (l+1)进行直方图均衡、高斯滤波及上采样得到图像E'(l+1)，设2a=A，2b=B尺寸变为A×B；

② 将第l+1级E'(l+1)和第l级细节图像D'l相加，得到A×B增强图像，并将其赋值第l级金字塔图像F'l；

③ 将F'l再顺序执行①～③，A变为a，B变为b，直至加到第1级，得到最终的重建图像F'0，尺寸M×N。

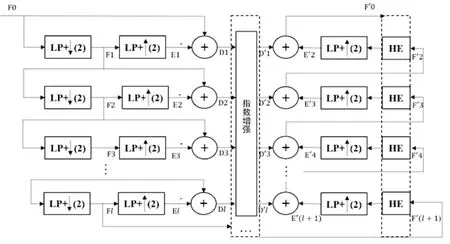
图2 高斯-拉普拉斯金字塔改进算法Fig. 2 Gauss-Laplace pyramid improvement algorithm

3 实验结果与分析

3.1 实验环境与数据

本文算法的实验环境是Matlab R2014b，CPU为i7-3770，主频3.4 GHz，内存8 GB。实验所选用的图像来自我院岛津RADSPEFDM平板DR拍出的胸部、盆腔和脊椎等纹理信息较多DR图像。限于篇幅，本文仅展示比较典型的胸部DR正位和侧位实验，图像尺寸1 440×2 160，并已隐去病人隐私数据。根据图像尺寸及式（6），预设指数函数参数p=0.7，a如表1所示。

表1 指数函数增益因子a的预设值Tab.1 Preset values of the exponential function gain factor a

3.2 实验结果与分析

实验结果如图3所示，从原始图像可以看出，胸片正位及侧位均亮度过高，肺部纹理不清晰，且脊椎等骨骼部分比较模糊；经过传统金字塔算法增强后的图像对比度提高，边缘骨骼与其背景之间的对比度变得更大，脊椎骨骼也比较清晰，胸部侧位图像效果不错，但正位亮度过低，不符合人眼视觉要求。经过本文提出的算法后，对比度得到进一步提高，胸部正位、侧位的肺部纹理十分清楚，图像比较有层次感，且图像亮度比较符合人眼视觉要求。

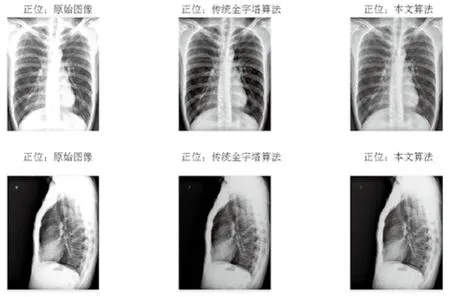
图3 实验结果对比Fig. 3 Comparison of experimental results

图像的视觉效果仅为主观评定，为定量测试算法实验效果，采用对比度衡量因子作为评价增强效果的客观标准，根据式(8)计算原图、传统算法、改进算法的对比度衡量因子。从表2可以看出原图对比度衡量因子较低，经过传统算法的图像对比度有一定提高，而经过本文算法的图像对比度得到进一步提高。

式中，Hproceed和Horiginal分别表示经过处理和原图的图像感兴趣区域的对比度。

表2 三种对比度衡量因子Tab.2 Three contrast factors

4 结论

本文在分析了传统高斯-拉普拉斯金字塔算法对于DR图像增强存在问题，并在考虑人眼视觉特性及获得更好细节增强效果的基础上，提出了一种基于金字塔的改进算法。该算法对DR图像的低频分量采用直方图均衡使图像灰度显示更加均衡；对高频分量采用指数函数增强，并根据不同塔层图像预设不同的增益权重。实验结果表明，改进算法提高了胸部、盆腔和脊椎等部位的DR图像的对比度，使图像更有层次感，获得了良好的图像增强效果。然而本算法还有些不足，即算法对于图像细节增强采取了人工预设增益因子的方法，不够智能。后续将研究分层自适应图像增强，使该算法更有实际价值。