含初始缺陷管中管侧向屈曲过程中的动态效应研究

张泽超，陈志华, ，刘红波, ，王 哲，刘凯月

(1.天津大学建筑工程学院，天津 300072；2.天津大学水利工程仿真与安全国家重点实验室，天津 300072)

高温高压下管道经常发生整体屈曲，当初始缺陷较小的时候，在管道发生整体屈曲之前通常发生瞬间的大变形，产生较大的应变，当能量释放后结构达到再次平衡，继而达到整体屈曲．

目前，针对管动力效应方面的研究主要集中于单层管道方面，刘润等[1]发现在一定温度下管线的整体屈曲会由第1种平衡状态跳跃到第2种平衡状态；施若苇[2]对比了管土作用及初始缺陷大小对管道动力响应的影响；王立忠等[3]得到管道在跳跃失稳发生时的动力响应；车小玉等[4]分析了在静力及动力阻尼条件下管道屈曲临界力的不同；Wang等[5]对单层管道整体屈曲动态效应进行了系统的研究；Erkmen等[6]建立了多尺度单层管道模型，得到了管道发生动态效应时的椭圆化现象；Lopes等[7]研究了在柔性管下运输带有谐振波的水流对管道的动力效应．

在深海油气开采领域中，为了适应深海高温高压工作条件，同时满足管道保温要求，PIP管道系统得到了广泛的应用．PIP系统由两根同心管道组装而成，在内外管道之间采用对中环支撑，确保内外管道相对位置固定，内外管形成的环形空间内填充不具备结构性能的保温材料．PIP系统的优势在于可以满足苛刻的绝热要求，当内管发生破裂时，外管可以成为系统的第2道防线，提高管道整体安全系数．

但是，目前针对管中管的动力效应研究极少见，对管中管的研究目前主要针对带初始缺陷管道水平屈曲及主动控制方面．Vaz等[8]基于单根梁微分控制方程，建立了非协调型管中管系统水平整体屈曲的微分控制方程，分析结果表明，管中管系统的整体屈曲形态与内外管的刚度、对中器的间距有很大关系；赵天奉[9]针对两处管中管系统实际工程，利用有限元技术分析了协调型和非协调型管中管的水平以及垂向整体屈曲性能，对于协调型(文中称为柔性连接管道)管中管系统，多发生由内管屈曲引发的整体屈曲，若对中器间距过大，则内管发生的低阶限制性屈曲将向高阶模态跃迁，从而危害管道安全；Goplen等[10]指出，分析和应用多层管道的重点就在于将其作为一个系统而不是作为相连的两个管道．

深海管中管在运营过程中，由于受到包括输送高压、深海压强、石油高温等各种极端荷载的作用，会存在管道整体热屈曲现象，而管道的整体屈曲发生过程中可能会伴随着动力效应的产生．管中管结构的内外管轴向力的合力代表了管中管系统的稳定性.随着内管温度逐渐增加，内管压力逐渐增大，而外管则承受拉力且随着温度增加拉力逐渐增加．内外管合力随着温度增加逐渐增加，达到极限屈曲轴力后便不再增加，说明结构发生屈曲，屈曲时的温度与初始温度之差称为管道发生屈曲的临界温差．基于有初始缺陷的管中管在整体热屈曲试验过程中产生的动力效应现象，本文分析了管道径厚比、初始缺陷长度以及管土作用对管道屈曲过程中动态效应的产生机理及作用变化规律，发现了各个因素与管道中点屈曲临界力、侧向弹出速度、侧向位移以及整体动能之间的关系，并针对此提出了控制动态效应的方法．

1 带有水平缺陷的管中管整体屈曲试验动态现象研究

1.1 管道参数的确定

采用油温加载装置，对小缺陷管中管在屈曲过程中的动力效应进行研究．参考已有的试验研究成果和试验设备性能，选用 6061-T6铝合金圆管模拟管道．管道长度为 9000mm，内外管的直径分别为36mm 和 62mm，管道内外管的厚度均为 3mm；在内外管间，沿轴向每隔 500mm 设置对中环，内外管间填充硅酸铝布作为保温材料．水平初始缺陷采用三角正弦曲线模拟，考虑不同的初始缺陷波长和幅值．由Maltby和Calladine提出的一种基于正弦函数的缺陷模式[11]为

式中：L是管道水平初始缺陷波长；l0是管道水平初始缺陷；v0为水平初始缺陷最大幅值．制作了 3个试验构件，构件参数如表1所示．

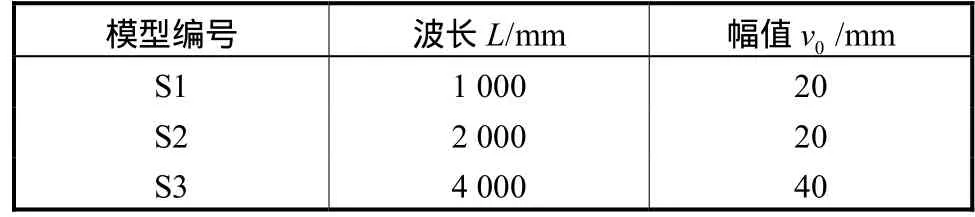
表1 试验构件参数Tab.1 Test component parameters

1.2 管道加工方法

由于双层有缺陷管道独特的构造，主要采取分段焊接拼装的加工方式进行制作，如图 1所示．首先将内外管沿轴向分为A、B、C 3段，其中A和C段为直线段，B段为缺陷段．内外管在B段通过滚压方式制作成设计缺陷大小，将外管截断为 A、B、C 3段，在B段处沿轴向切开，然后将布置好应变片的内管放入外管后，沿外管截断处进行焊接．

图1 外管及内管加工Fig.1 Processing of inner and outer pipes

1.3 试验现象分析

如图 2所示，随着温度荷载的增加，除了构件规格为波长 1000mm、幅值 20mm 的管道外，其他两根管道均发生向屈曲段凸起一侧方向的位移，不同规格的管道侧向位移激发方式不同，位移激发初始温度也不同．构件规格为波长 1000mm、幅值 20mm 的管件由于构件幅值较小，在加载过程中发生了突然的反向移动，此时动力效应较为明显．其主要原因是对于缺陷波长较小的管道，在热加载过程中由于管道在缺陷处变形的累积，会在缺陷的起止点处与管道轴向形成内弯变形，管道轴力会产生与缺陷方向相反的分量，从而导致管道发生突然的反向位移．

图2 管道油温加载结果Fig.2 Results of heating-up process on pipes

1.4 试验结果分析

图 3中为 S1、S2、S3管道在加载过程中的位移全过程，其临界温差分别为 70.6℃、50.3℃和44.6℃．S1和S3管道在加载过程中各测点的位移方向基本一致，S2管道在温差较低时管道呈现波浪形位移变形，这与管道加工时的误差有关，管道自身在5500mm处有初始弯曲缺陷．通过对比图3(a)和(b)可知，在管道幅值相同的情况下，由于 S1管道的水平缺陷长度较S2管道的长度减少了1000mm，缺陷值较小，因此 S1管道各测点在临界屈曲发生前突然发生与缺陷幅值方向相反的整体反向侧移，动态效果十分明显；对比图 3(b)和(c)可知，由于试件 S2和S3的缺陷值较大，缺陷长度占整体长度的缺长比分别为 22%和 44%，相比 S1管道试件缺长比提高了11%和 33%，虽然幅值与波长的比值由 2%下降到1%，但是并没有减少由于缺长比较小导致的管道在屈曲过程中的动态效应．由此可知，对于整体长度固定的管道，缺陷长度的大小对管道整体屈曲过程中的动态效应起到了主要作用．

图3 各阶温差下管中管各测点侧向位移Fig.3 Lateral displacement of PIP measurement points under different temperature differences

2 管中管动态效应数值模型的建立

2.1 模型参数的选取

参照已有管道试验，该试验采用油温加载装置，研究管中管结构在温度荷载作用下的整体屈曲性能.本文对其试验试件管道进行有限元模拟，试验管道长度为 9 000 mm，内、外管的直径分别为 36 mm 和62 mm，管道内外管的厚度均为 3 mm．利用ABAQUS有限元软件，建立管中管系统的有限元模型，针对小缺陷管中管在整体屈曲过程中的动力效应进行研究．建立管中管有限元模型，深海输油管道在结构上可以定义为超细长结构，也就是其长度方向的尺寸远远大于另外两个方向(即管道截面)．在水平屈曲分析过程中，海床的刚度采用传统整体屈曲理论的刚性海床面假设，管道的两端全部为铰接，管道长度为 9000mm，管道整体屈曲的激发方式为采用升温的方式．

模型中采用 PIPE21梁单元模拟内外管道，在模型中，采用单节点 ITT单元模拟对中环，用来模拟内外管之间的接触作用．ITT单元附着在内管梁单元的节点上，间隔 500mm，与之对应，存在一条虚拟的滑移线附着在外管上，滑移线由外管节点构成，见图 4.水平初始缺陷都与试验构件相同，采用三角正弦曲线模拟．模型材料参数的选取如表2所示．

图4 数值模型Fig.4 Numerical model

表2 模型参数Tab.2 Model parameters

本文中有限元模型的计算流程为：①管道就位过程(弧长法静力分析)；②管道侧向屈曲过程(隐式动力分析)．

计算采用 ABAQUS的动力隐式求解进行计算，在计算中采用瑞利阻尼，即

式中：a和b是由用户定义的参数；C为瑞利阻尼矩阵；M为系统质量矩阵；K为刚度矩阵．

根据文献[3]，取a＝0.5，β＝0．对内管采用线性加温的方式，加载速率为1/2 400℃⁄s，管道从 0℃经过 2400步逐步加载到 100℃，尽量减小升温速率过快引起的管道内力突变．

2.2 模型验证分析

将试验管道和数值模型管道的编号按照以下定义：S/M(试验/数值模型编号)-l0(初始缺陷波长)-v0(幅值)．对于缺陷长度不同的管道模型，选取模型管道与试验管道的中点位移进行结果对比．由图5可知，在相同温度下，数值模型与试验节点位移的变化规律及增长趋势相同，临界屈曲温度及管道中点临界侧向位移的试验结果与数值分析结果差值幅值在15%左右，结果较为准确，误差产生的原因主要为试验中砂石含有杂质，管土作用数值变化产生波动，由此可以验证数值模型建立方法的正确性．

图5 中点位移试验结果与数值分析结果对比Fig.5 Comparison of midpoint displacement between test result and numerical result

3 不同参数影响下管道动态效应结果分析

跳跃屈曲的过程就是系统应变能(strain energy)的释放过程[12]．根据虚功原理，管道的平衡方程[13]可以表达为

式中：为内能增量的变分；为外力功增量的变分．

管道在屈曲过程中的能量转化方程[14]为

式中：Et为总能量；Es为应变能；Ek为动能；Ew为外部功．

通过参数化建模，对总长度为 9000mm 的管中管进行管道屈曲过程中的能量转换、临界温度、轴力及侧向位移分析．

3.1 径厚比影响分析

对于缺陷波长L＝1000mm、幅值v0＝20mm 的管道进行参数化分析，外管直径D＝60mm，内管壁厚t＝3mm，定义内管径厚比h＝d/t，内管径厚比h取值分别为 30/3、35/3、40/3、45/3、50/3和 55/3．

如图 6所示，内、外管轴力之和代表了管道的稳定性，随着管径增大，管道临界屈曲温度及临界屈曲力降低，管道在后屈曲阶段内、外轴力之和趋于平缓，管道稳定性增强．

图6 管道中点轴力与温差的关系Fig.6 Relationship between axis force and temperature difference of midpoint of pipe

从图 7可知，当内管径厚比取 10时，临界温差为 44.7℃，管道侧向位移突然发生跳跃，由正缺陷方向侧移25mm跳跃到负缺陷方向51mm处，并在此处发生不断震动，震动时间约 0.4s；而当内管径厚比大于 35/3时，管道在屈曲前后仅沿正缺陷方向进行侧向移动，屈曲发生时的侧向位移突变值由 42.1mm降至 15.5mm，位移突变值呈线性减小，管道侧移突变值减小到20%且变形趋于稳定．

图 8为不同径厚比下管道中点的侧向位移，当h＝30/3时管道中点侧向位移为-59mm，临界屈曲位移方向与管道缺陷方向相反，当h＝35/3时管道中点侧向位移为 42mm，达到正的最大值，此后径厚比作用减弱．

图 9说明了不同径厚比对管道中点的侧向速度的影响，当内管径厚比为 10时，在升温过程中，管道中点的侧向速度变化波动较大，峰值相差为102mm/s，当内管径厚比为 55/3时，速度差为0.8mm/s．综上可知，在升温过程中，随着内管径厚比的增大，整体侧向速度降低，管道逐渐趋于稳定．

图7 管道中点侧向位移与温差的关系Fig.7 Relationship between lateral displacement and temperature difference of midpoint of pipe

图8 管道中点侧向位移与管径的关系Fig.8 Relationship between lateral displacement and diameter of midpoint of pipe

图9 管道中点侧向速度与温差的关系Fig.9 Relationship between lateral velocity and temperature difference of midpoint of pipe

由图 10和图 11可知，当内管径厚比为 10时，管道整体动能最大为 96.4J，而随着内管径厚比的增加到 55/3时，动能减小到 8×10-3J，此时，其动力效应可以忽略不计．由此可知，随着内管径厚比的增加，管道的动力效应明显减弱，当内管径厚比由 35/3提升至55/3时，管径大小提高了36.4%，但是整体动力效应可以降低95.2%．

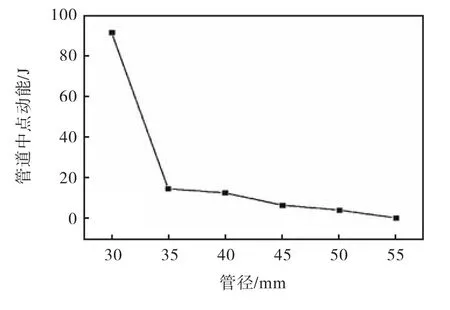
图10 管道中点动能与管径的关系Fig.10 Relationship between kinetic energy and diameter of midpoint of pipe

图11 管道整体动能与温差的关系Fig.11 Relationship between kinetic energy and temperature difference of global buckling of pipe

在外径不变的前提下，内管径厚比的增加就是内管管径的增加，也就是内管的屈曲临界力和抗弯刚度的增加．在h＝30/3时，内外管管径之比为 0.5，在管道整体升温后，外管拉力值相对内管压力值增加速度明显，因此产生负向位移；当径厚比大于h≥35/3时，可以有效减弱管道屈曲过程中的动力效应，管道整体动能值处于较低水平；在h＝35/3之后再增加内管，对管道降低动能作用不明显，且浪费材料，因此径厚比值为 12.0且内外管管径之比大于 0.5为最优值．

3.2 初始缺陷影响分析

选取内管管径为 30mm、外管管径为 60mm 的管道，缺陷幅值v0＝20mm，缺陷波长取 600mm、800mm、1000mm、1200mm、1300mm、1400mm进行分析．

图 12为管道中点轴力与温差之间的关系，分析可得屈曲临界温度从L＝600mm时的34.3℃提高到L＝1300mm时的70.9℃，随着缺陷波长的增加而增加，当缺陷波长L增加至 1400mm 时，临界温度为70.5℃，而内外管轴力之和较L＝1300mm突变值降低了 90%以上，因此可知，在缺陷波长L＝1400mm之后，管道整体稳定性能提高．

图12 管道中点轴力与温差的关系Fig.12 Relationship between axis force and temperature difference of midpoint of pipe

由图 13可知，当缺陷波长为 600～1300mm时，在屈曲发生后，管道会发生突然的向负缺陷方向的侧移，而当L＝1400mm 时，在发生屈曲后，管道位移方向依然为沿正缺陷方向．由此可知，当管道的其他参数一定时，随着缺陷波长的增加，管道临界屈曲温度提高，管道侧向位移会发生突变．

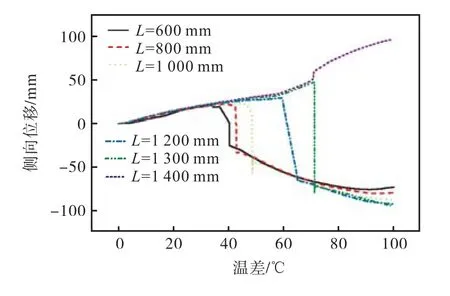
图13 管道中点侧向位移与温差的关系Fig.13 Relationship between lateral displacement and temperature difference of midpoint of pipe

对图 14分析可得，当缺陷波长L从 600mm提高至 1300mm 时，缺陷波长提高了 116.7%，而管道侧向位移值提高了 206.6%，当缺陷波长L＝1400mm 时，侧向位移值为 58.9mm．由此可知，管道缺陷波长较小(L≤1300mm)时，整体屈曲发生后侧向位移发生负缺陷方向移动，其值大小随着管道缺陷波长L的增加而增大，而当管道缺陷波长较大(L≥1400mm)时，管道向缺陷正向发生侧向位移．

图15为管道中点侧向速度与温差之间的关系，分析可知当缺陷波长L＝600mm 时，管道侧移速度为 16mm/s，随着缺陷波长逐渐增加到 1300mm，侧向位移速度达到最大值为102mm/s，而L＝1400mm时速度为 3.5mm/s，基本可以忽略．由此可知，在初始缺陷波长小于某值时，随着缺陷波长提高116.7%，侧向移动速度增加了 575%，而缺陷波长大于等于1400mm时，侧向位移速度平稳，管道逐渐稳定．

图14 管道中点侧向位移与缺陷波长的关系Fig.14 Relationship between lateral displacement and defect wavelength of midpoint of pipe

图15 管道中点侧向速度与温差的关系Fig.15 Relationship between lateral velocity and temperature difference of midpoint of pipe

由图16和17可知，当缺陷波长L＝600mm时，动能为 5.72J，随着波长增加到 1300mm时，在屈曲后，管道动能达到最大值 577J，而缺陷波长L＝1400mm时，动能最大值为0.4J，动力效果基本可以忽略．由此可知，以缺陷波长1400mm为临界值，当小于临界值时，随着缺陷波长的增加，管道屈曲后动态表现逐渐增强，总动能提高到100倍左右；而越过临界值后管道动态效应明显降低，整体屈曲过程趋于稳定．

图16 管道中点动能与缺陷波长的关系Fig.16 Relationship between kinetic energy and wavelength of midpoint of pipe

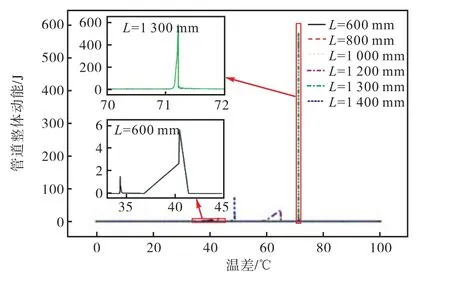
图17 管道整体动能与温差的关系Fig.17 Relationship between kinetic energy and temperature difference of global buckling of pipe

因此，以缺陷长度L＝1300mm 为临界长度，缺陷长度与整体管道长度比值为0.15，管道动能在临界长度前呈线性增长，之后整体动能迅速降低，且管道中点屈曲位移由负向变为正向．这是因为其他条件不变而仅改变初始缺陷大小，可以将管中管简化为带有初始缺陷管道轴心受压的整体稳定问题；对含有初始弯曲缺陷压弯构件分析可知初始缺陷越大，其压杆临界力越小．内管整体受压带动外管发生屈曲，由于轴向及侧向管土作用，管道会有向中点缺陷处累积变形的趋势．在临界缺陷长度以下时，外管拉力增长速度较内管压力增加速度快，会在缺陷起止点处产生较大的负向力和弯矩，从而产生负向位移；当超过临界长度后，管道内管轴力增长速率大于外管拉力，管道整体受压，管道中点位移为正．虽然当管道初始缺陷波长较大时管道更容易发生屈曲，但其动力效应不明显，所以为了消除动态效果，可增大初始缺陷波长．

3.3 管土作用影响分析

取内管管径为 30mm、外管管径为 60mm、波长L＝1300mm、幅值v0＝20mm 的管道，其管土摩擦系数分别为 0.1、0.2、0.3、0.4、0.5、0.6．

由图 18可知，随着管土摩擦系数的增加，管道整体屈曲发生时的轴力之和由-1451.8N提高至-1742.2N，管土摩擦系数提高了6倍，而轴力之和提高了20.1%，临界屈曲温度由66.7℃提高至77.7℃，提高了 16%；当摩擦系数μ取 0.5、0.6时，轴力之和发生较大突变，轴力之和的差值由μ＝0.1时的20.3N增至 499.6N，且μ＝0.5与μ＝0.6时，轴力突变值仅相差 10.5N．由此可知，随着管土摩擦系数增加，外管与海床的摩擦力增大，限制了管道轴向力的发展．

对图19和图20进行分析，当μ＜0.5时，在加载过程中，管道中点只沿缺陷正方向移动，而当μ≥0.5时，在屈曲发生后，管道中点突然跳跃到缺陷负方向．当摩擦系数μ从 0.1提高至 0.6时，侧向位移值由98.4mm变化到-76.0mm，变化177.5%．

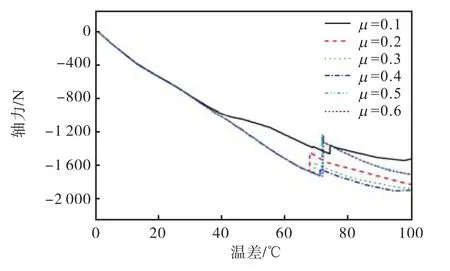
图18 管道中点轴力与温差的关系Fig.18 Relationship between axis force and temperature difference of midpoint of pipe

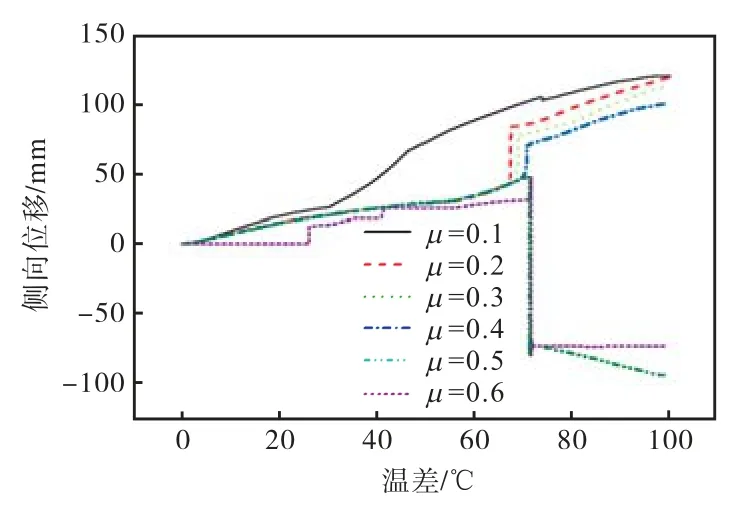
图19 管道中点侧向位移与温差的关系Fig.19 Relationship between lateral displacement and temperature difference of midpoint of pipe

图20 管道中点侧向位移与摩擦系数的关系Fig.20 Relationship between lateral displacement and friction coefficient of midpoint of pipe

对图 21分析得到，当μ＝0.1时，管道中点侧向移动速度最小，且波动最小，其峰值为8mm/s；当μ＝0.6时，管道中点侧向移动速度达到最大值101mm/s，且在屈曲前后反复波动．

由图22和23可以得到，在管道发生整体屈曲过程中，管道动能时刻变化，管道在整体屈曲前后动力效果显著．当μ＝0.1时动能最小为 11.8J，当μ＝0.6时动能达到最大为 571J，整体提高了 48倍左右．可知管土摩擦系数的影响对管道动力效果显著．

通过管土作用影响分析可知，管道发生热屈曲后，管道平直段会有向屈曲段挤进的趋势，轴向摩擦力约束了管道平直段的挤进，从而抑制了屈曲变形.随着摩擦系数的增加，管道发生侧向屈曲时需要克服的摩擦力越大，平直段内管道的轴力就越大．摩擦系数越大，管道发生失稳时的动力响应越明显，管道弹出的速度越大．

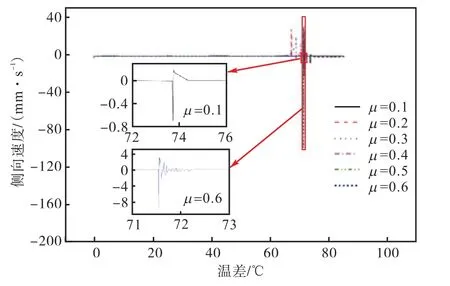
图21 管道中点侧向速度与温差的关系Fig.21 Relationship between lateral velocity and temperature difference of midpoint of pipe

图22 管道中点动能与摩擦系数的关系Fig.22 Relationship between kinetic energy and friction coefficient of midpoint of pipe

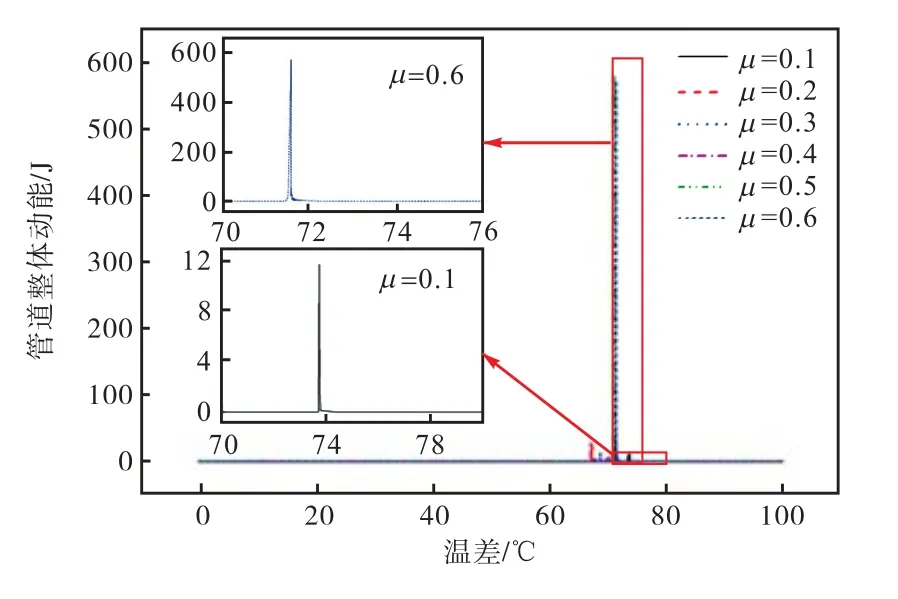
图23 管道整体动能与温差的关系Fig.23 Relationship between kinetic energy and temperature difference of global buckling of pipe

4 结 论

(1) 基于试验得到管道中点加载全过程数据，建立了管中管 ABAQUS数值模型，通过对比发现，数值计算和试验分析结果相吻合，验证了有限元分析方法的正确性；

(2) 找到了径厚比最佳临界点 12.0及内外管管径之比大于 0.5，可以为管中管的内、外管管径选值提供参考；

(3) 对管道缺陷波长进行研究，通过对比不同缺陷波长下管道动能值，得到了缺陷波长与管道长度动能临界比值0.15，为管道的合理铺设选型提供依据；

(4) 对比了不同管土摩擦系数下管道中点侧向位移、弹出速度以及整体动能值，对管土作用下管道屈曲机理进行分析，发现管土作用对管道整体动态效应影响显著．

[1] 刘 润，刘文斌，谭振东，等.含初始缺陷海底管线整体屈曲的分析和数值模拟[J].中国造船，2015，56(1)：159-167.

Liu Run，Liu Wenbin，Tan Zhendong，et al.Analytical and numerical solution on global buckling of imperfect submarine pipeline[J].Shipbuilding of China，2015，56(1)：159-167(in Chinese).

[2] 施若苇.海底管道热屈曲及管土相互作用研究[D].杭州：浙江大学建筑工程学院，2014.

Shi Ruowei.Global Buckling of Subsea Pipelines and Pipe-Soil Interaction[D].Hangzhou：School of Architectural Engineering，Zhejiang University，2014(in Chinese).

[3] 王立忠，王宽君，施若苇.管道热屈曲动力过程数值模拟[J].海洋工程，2015，33(5)：73-80.

Wang Lizhong，Wang Kuanjun，Shi Ruowei.Numerical simulation for the dynamic process of pipeline buckling[J].The Ocean Engineering，2015，33(5)：73-80(in Chinese).

[4] 车小玉，段梦兰，增光霞，等.双层管道整体屈曲实验研究及数值模拟[J].应用数学和力学，2014，35(2)：188-199.

Che Xiaoyu，Duan Menglan，Zeng Guangxia，et al.Experimental study and numerical simulation of global buckling of pipe-in-pipe systems[J].Applied Mathematics and Mechanics，2014，35(2)：188-199(in Chinese).

[5] Wang Zhe，Chen Zhihua，Liu Hongbo.On lateral buckling of subsea pipe-in-pipe systems[J].International Journal of Steel Structures，2015，15(4)：881-892.

[6] Erkmen R Emre，Mohareb M，Afnani A.Multi-scale overlapping domain decomposition to consider elastoplastic local buckling effects in the analysis of pipes[J].International Journal of Structural Stability and Dynamics，2017，17(1)：1750015-1-28.

[7] Lopes J L，Paidoussis M P，Semler C.Linear and nonlinear dynamics of cantilevered cylinders in axial flow.Part2：The equations of motion[J].Journal of Fluids and Structures，2002，16(6)：715-737.

[8] Vaz M A，Patel M H.Lateral buckling of bundled pipe systems[J].Marine Structures，1999，12(1)：21-40.

[9] 赵天奉.高温海底管道温度应力计算与屈曲模拟研究[D].大连：大连理工大学，2008.

Zhao Tianfeng.Research on Thermal Stress and Buckling of HT Submarine Pipelines[D].Dalian：Dalian University of Technology，2008(in Chinese).

[10] Goplen S，Fyrileiv O，Grandal J P，et al.Global Buckling of pipe-in-pipe：Structural response and design criteria[C]//30th International Conference on Ocean.Rotterdam：ASME，2011：777-784.

[11] 王 哲，马克俭，陈志华，等.深海管道整体屈曲研究综述[J].天津大学学报：自然科学与工程技术版，2014，47(增)：17-23.

Wang Zhe，Ma Kejian，Chen Zhihua，et al.Overview of global buckling of deep-sea pipeline[J].Journal of Tianjin University：Science and Technology，2014，47(Suppl)：17-23(in Chinese).

[12] 陈 骥.钢结构稳定理论与设计[M].北京：中国科学出版社，2003.

Chen Ji.Stability of Steel Structures Theory and Design[M].Beijing：Chinese Science Press，2003(in Chinese).

[13] 余建星，李智博，杜尊峰，等.深海管道非线性屈曲理论计算方法[J].海洋工程，2013，31(1)：54-60.

Yu Jianxing，Li Zhibo，Du Zunfeng，et al.Theoretical calculation method of the nolinear buckling of deepsea pipes[J].The Ocean Engineering，2013，31(1)：54-60(in Chinese).

[14] Tonkovi Z，Skozrit I，Sori J.Fracture of Nano and Engineering Materials and Structures[M].Netherlands：Springer，2006.