沙纹床面振荡流边界层的三维格子玻尔兹曼模拟研究

周志博 ，张庆河，张金凤

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300072；2.交通运输部天津水运工程科学研究院海洋水动力研究中心，天津 300456)

沙质海岸海床床面在波浪作用下经常呈现沙纹形态，沙纹的出现会显著增加床面对底部水体的阻力，使波浪底部边界层流动产生明显改变．因此，对沙纹床面振荡流边界层流动特性的深入认识，是研究存在沙纹情况下的泥沙运动规律、准确计算输沙量等问题的前提．为此，不少学者通过实验、数值模拟和现场观测等手段对沙纹床面振荡流边界层的水流及其紊动特性进行了研究．实验研究方面，学者们通过激光流速仪(laser Doppler anemometry，LDA)[1]、多普勒剖面流速仪[2]等设备测量了沙纹床面边界层流速、紊动强度和床面切应力等，为认识沙纹床面振荡流边界层流动奠定了基础．在数值模拟方面，受到计算资源的制约，早期的工作主要进行了二维数值模拟研究[1,3-7]．由于沙纹床面振荡流边界层内的流动通常为高雷诺数三维紊流，只有通过三维数值模拟才能较全面、细致地反映复杂的振荡流边界层流动，为此，近年来人们开始基于 DNS[8]、LES[9]等方法开展三维数值模拟研究，以加强对沙纹边界层复杂紊动特性的认识．然而，由于沙纹振荡流边界层流动的复杂性，对沙纹存在导致的流动分离、涡旋发展，沙纹床面切应力的变化过程和沙纹形状摩阻与肤面摩阻在总拖曳力中的贡献等问题仍有待深入研究．

格子玻尔兹曼(lattice Boltzmann，LB)方法是近年来发展迅速的一种新型数值模拟方法，可以从介观角度描述宏观流体的运动，具有可以高效并行计算、易于处理复杂几何边界等优点．二维LB模型对光滑平床振荡流边界层获得了较好的模拟结果[10-12]．对于粗糙床面振荡流问题；丁磊等[13]采用三维LB方法研究了振荡流边界层中颗粒的受力，并对球形颗粒规则排列构成的粗糙平床上振荡流边界层流动进行了三维全尺度 DNS模拟，研究了粗糙床面的阻力特性[14]；周志博等[15]建立了基于Smagorinsky大涡模拟方法的三维LB模型，研究了粗糙床面振荡流边界层的紊动特性和床面粗糙参数．

然而对于紊动更加复杂的沙纹床面振荡流边界层流动，通常振幅雷诺数较高，采用 DNS求解计算量巨大，而传统的LES方法，如Smagorinsky模型则不能完全满足壁面律[16]．为了能更好地反映近壁紊动特性，学者们[16]提出了一种新的壁面自适应局部涡黏(wall-adapting local eddy-viscosity，WALE)模型，该模型的建立不需要给定距离壁面的距离，也不需要引入衰减函数或求解动力过程，并且能合理地描述转捩流态的特性，更适用于复杂边界情况[16-17]．因此本文将 WALE模型引入到三维 LB模型，以更好地描述沙纹振荡流边界层流动．

1 数值方法

1.1 格子玻尔兹曼方法

格子玻尔兹曼是在介观层面构建离散速度模型，即格子模型，通过控制虚拟粒子在格子模型中的演化使流体表现出宏观运动方程控制的性质．LB方法的控制方程，即LB方程为

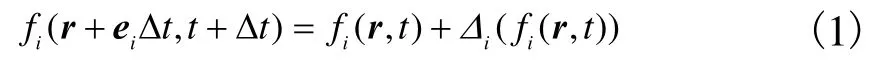
式中fi(r,t)为t时刻在r位置处沿i方向的密度分布函数；ei为沿i方向的离散速度；Di为碰撞算子，表示虚拟粒子的碰撞规则．

根据碰撞算子的选择不同，可以将LB模型分为单松弛时间(single-relaxation-time，SRT)模型[18-19]和多松弛时间(multiple-relaxation-time，MRT)模型[20-21].LBGK模型[18-19]是 SRT模型中最具代表性的一种模型.Ladd等[22]在研究颗粒流问题时发现，采用LBGK模型的计算结果在流固边界处容易产生误差，认为这是在整个计算域采用同一个松弛时间造成的，并对LBGK模型进行了改进，提出了双松弛时间(tworelaxation-time，TRT)模型．该模型的控制方程可以表示为

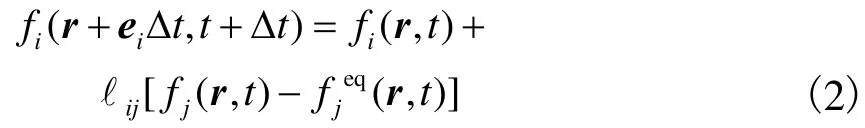
密度分布函数与流体宏观物理量，即流体密度r、动量密度j=ru和动量通量Π之间的关系为

式中u为流体宏观速度矢量．

离散速度模型是反映虚拟粒子速度的离散模式.本文采用D3Q19模型，各方向离散速度表达式为

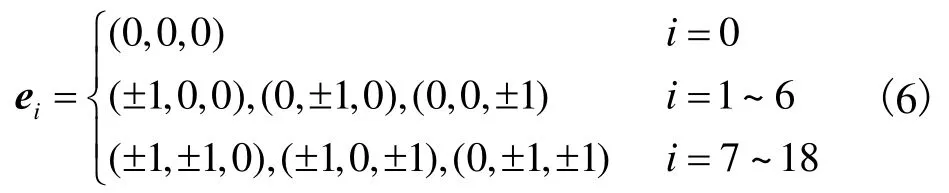
1.2 边界条件

1.2.1 周期性边界条件

在LB模型中，周期性边界上未知的分布函数可以通过虚拟粒子在格子模型中的运动规则直接确定，当代表流体的虚拟粒子从一侧周期性边界离开计算区域时，在下一个时间步会从计算区域另一侧的周期性边界进入流场．以x方向采用周期性边界为例，计算域在x方向划分Nx个网格，该格式可表示为

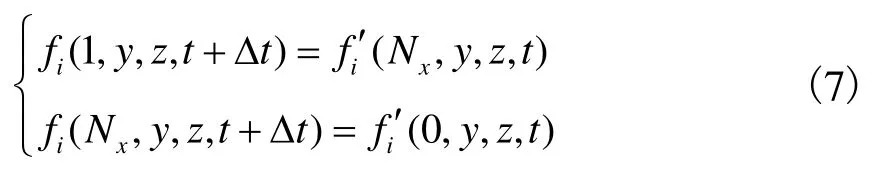
式中fi为未知分布函数，其离散速度ei方向指向流场内部．

1.2.2 自由滑移边界条件

采用镜面反射格式处理 LB模型中的自由滑移边界．当粒子由流体格点迁移至边界格点后，沿着边界法线方向的对称方向反射．该格式可以表示为

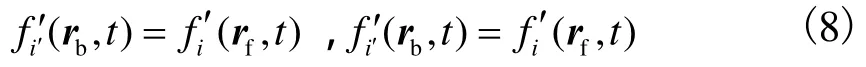
式中：ei¢为ei关于边界法向方向镜像对称的离散速度；rb和rf分别表示边界格点和流体格点的位置，rb=rf+eiDt．镜面反射格式的粒子在自由滑移边界上不进行碰撞，只进行分布函数的迁移．按镜面反射格式处理的边界法向速度分量为0．

1.2.3 固壁边界条件

采用具有二阶精度的 Half-way反弹格式处理沙纹表面的固壁边界[23]．Half-way反弹格式的边界位于相邻的固体格点与流体格点的中心处，即(rb+rf) /2处．具体的处理方式表示为

式中表示i的反方向．Half-way反弹格式的物理图像为：在t时刻，流体节点处经过碰撞后速度指向边界的粒子进行迁移，经过Dt/2后到达处的边界，然后执行反弹，再经过Dt/2后重新到达流体格点位置．图 1为 Half-way反弹格式的曲线边界示意[24]，为方便描述，这里以二维情况说明．图中方形格点为采用 Half-way反弹格式的边界格点，位于流体格点和固体格点之间，黑色实线所示为实际边界，模型中通过空心方块连接而成的边界近似表示.

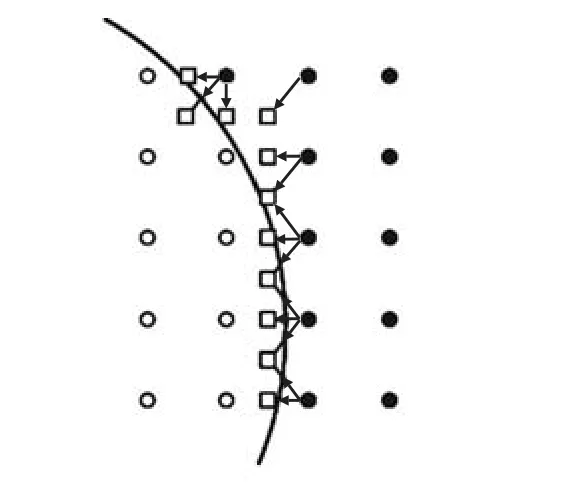
图1 Half-way反弹格式曲线边界示意Fig.1 Curved boundary of Half-way bounce-back boundary condition

此外，固壁边界受到流体的作用力可以通过动量交换法[25]计算．对某固壁边界点，相邻的流体格点向边界方向迁移的分布函数为，对应的动量为；经过反弹后离开固壁边界点的分布函数为，对应的动量为；由动量定理和力的相互作用原理可知，固壁边界点受到的作用力大小为；根据反弹的规则，，在 LB模型中Dt＝1时，固壁边界点所受作用力大小为．

1.3 大涡模拟在LBM中的实现

大涡模拟(large eddy simulation，LES)方法是解决高雷诺数流动模拟的常用方法之一，其主要思想是直接模拟大尺度的紊动，而小尺度紊动的影响通过亚格子模型反映，既可以得到比雷诺平均方法更多的大尺度涡结构的信息，又可以比直接数值模拟节省大量的计算量[26]．在 LES模型中通过过滤尺度区分直接求解的大涡尺度和待模化的小涡尺度，在LB模型中过滤尺度常选为格子长度．LB模型中实现大涡模拟需要引入紊动黏度，以反映小尺度涡对大尺度涡的影响，并通过将松弛时间变为考虑了紊动黏度影响的总松弛时间以增大模型中总的黏度.总的黏度由和相加而得

紊动黏度通常由速度特征尺度与长度特征尺度的乘积确定．假设在亚格子尺度动能方程中能量的产生和耗散作用平衡，速度尺度为，长度尺度为为LES模型算子，紊动黏度为

式中CX为 LES模型的常数．加入了紊动黏度之后，总松弛时间为

将式(10)和(11)代入式(12)中可得

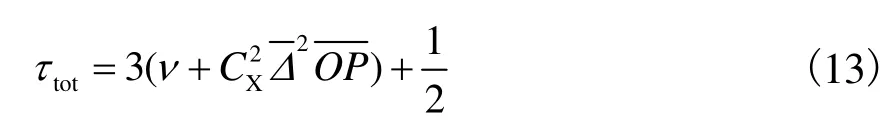
不同的LES模型所选取的模型算子不同，其中最易于实现的是 Smagorinsky模型．其模型算子由速度张量的对称部分．

式中Cs为 Smagorinsky常数；为可解尺度流动的应变率张量；为网格滤波算符．

然而 Smagorinsky模型具有一些天然的缺陷，如模型参数Cs需要先验确定，以及在层流区紊动黏度仍不为0，不符合物理实际等．

WALE模型是一种新的壁面自适应局部涡黏模型，可以更好地反映近壁紊动特性[16]．该模型算子在引入速度梯度张量的对称部分，即变形率张量的基础上，又引入了速度梯度张量的不对称部分，即转动张量，其模型算子为

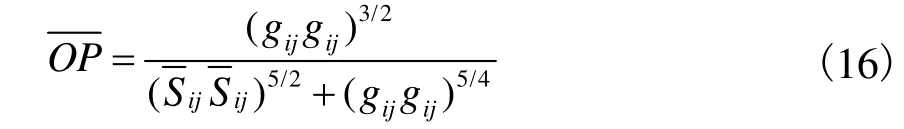
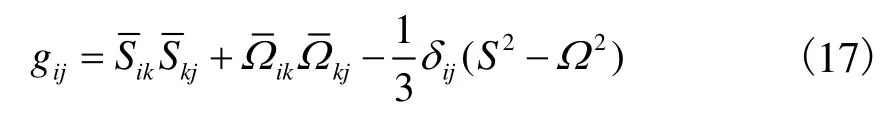
式中转动张量为

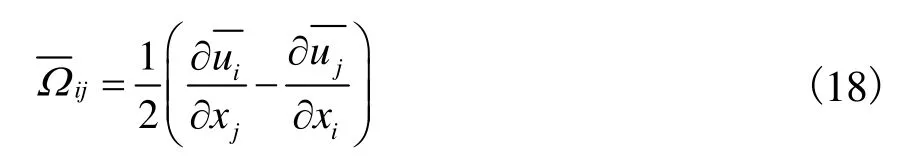
模型常数.WALE模型的准确性和精度已经过大量研究验证[16-17,27]，在基于 TRT模型[22]的计算程序中分别加入 Smagorinsky模型和 WALE大涡模拟模型，对沙纹床面振荡流边界层的紊动流场进行模拟，对结果进行比较．

2 模型设置

选取Fredsøe等[1]固定沙纹波浪水槽实验数据进行模拟．模型参数按照实验参数设置，以水质点轨道运动幅值a为特征长度，振荡流水质点运动速度幅值U0为特征速度，无量纲化的沙纹长度/a＝2.2，沙纹坡度为沙纹波高，振幅雷诺数Rea＝23,163．计算区域顺流向长度Lx=4.4a，即区域内包含两个完整沙纹，可以保证计算区域宽度足以包括较大尺度涡旋结构．计算区域顶边界设为自由滑移边界，与顺流向垂直的两个边界和两个侧边界均设置为周期对称边界，底边界即沙纹床面表面设置为无滑移的固壁边界．沙纹表面由圆弧组成，沙纹顶峰尖锐，谷底平坦．计算区域示意图见图 2．模型各方向的格子数Nx、Ny和Nz分别为 432、412和 432．振荡流流动采用周期性的压力梯度驱动．算例共模拟 25个振荡周期，其中前 10个周期用来获得稳定的流场，后面15个周期用于结果分析．算例在天河1号超算中心运行，使用72个CPU，每个算例运行约77h．

/＝0.159，h

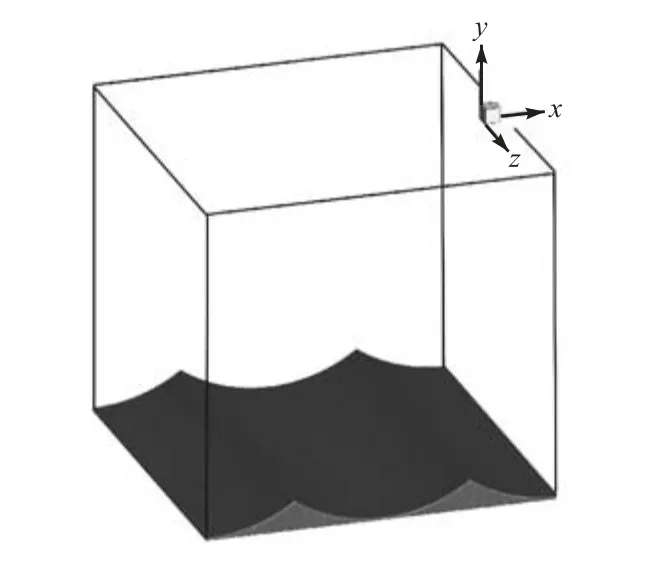
图2 计算区域示意Fig.2 Computational domain

3 结果和分析

3.1 平均流速分布

对瞬时水平流速的垂向分布进行系综平均和空间平均，得到图3所示4个特征位置处的平均流速分布．图 4显示了不同沙纹位置处平均流速的垂向分布与实验结果的比较，其中模拟值包括WALE模型和Smagorinsky模型的结果．图中纵坐标的起点为计算底边界，即沙纹谷底位置．实线为WALE模型结果，虚线为 Smagorinsky模型结果，圆圈为实验结果．受沙纹形状的影响，在各沙纹位置处的流速分布呈现出明显的区别．两种大涡模拟模型的结果存在较明显的差别，Smagorinsky模型在各沙纹表面位置的多个相位结果偏大，而 WALE模型的平均流速分布更接近实验结果．

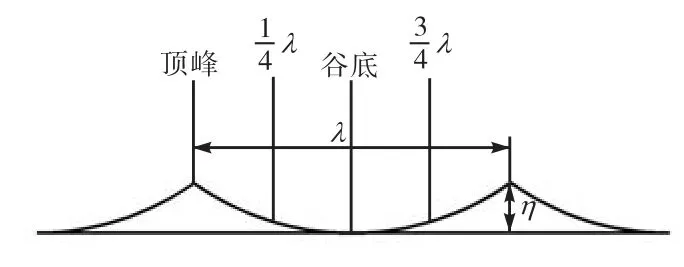
图3 沙纹位置示意Fig.3 Locations of sand ripple

3.2 紊动强度

图5为采用WALE模型和Smagorinsky模型得到的沙纹各位置顺流向平均紊动强度的垂向分布与实验结果的比较．图中纵坐标的起点为计算底边界，即沙纹谷底位置．在沙纹 1/4位置，如图5(a)中°时刻，Smagorinsky模型结果中紊动强度大值出现的范围明显大于实验结果，而 WALE模型的结果与实验结果更加接近．在沙纹谷底位置，如图5(d)中时刻，紊动强度分布具有双峰的特征[1,9]，其中下方的峰值产生于边界层，上方的峰值由沙纹顶峰处的剪切层分离造成．WALE模型结果尽管幅值大于实验结果，但很好地反映了该位置处的这一特征，而 Smagorinsky模型结果不仅明显偏小，且没有能够反映双峰特征．简单的 Smagorinsky模型在应用于沙纹床面的边界层流动模拟时，沙纹背流侧坡面和谷底位置的平均流速分布和紊动强度结果均与实验结果存在较明显的差异．相比Smagorinsky模型，WALE模型不仅考虑了应变率张量，而且包含了转动张量的影响，更适用于复杂边界流动的模拟，较好地反映了边界层内，特别是沙纹背流侧流动分离区域的紊动特征．根据 WALE模型和Smagorinsky模型的比较结果，在沙纹床面振荡流边界层的模拟中，WALE模型可以更好地反映沙纹这种尺度更大的粗糙单元上方边界层的流动特性和紊动特性．下文结果来自于WALE模型的模拟．

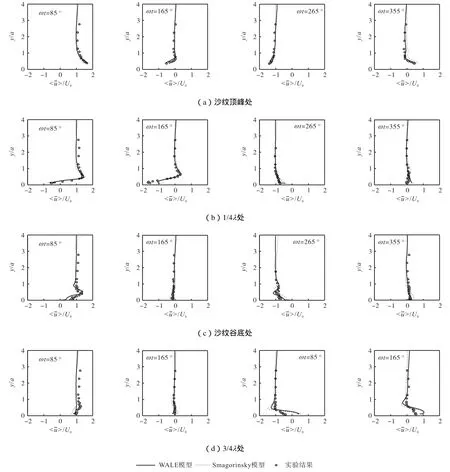
图4 沙纹各位置处平均流速分布Fig.4 Average velocity distributions at different locations of sand ripple

3.3 压力分布和形状摩阻系数

沙纹的存在使边界层在沙纹顶峰背后产生流动分离，形成涡旋，而涡旋在沙纹背流侧的形成和发展使沙纹背流面受到负压作用．沙纹床面所受的形状拖曳力Fp就是由沙纹两侧坡面所受的压力差产生，可以通过沙纹表面各处正向压力水平分量的积分来计算．无量纲的形状摩阻系数定义为

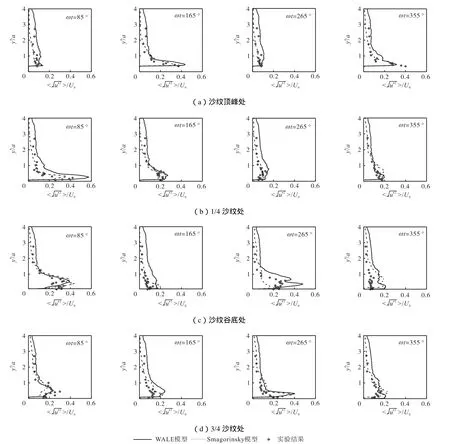
图5 沙纹各位置处平均紊动强度分布Fig.5 Average turbulent intensity distributions at different locations of sand ripple

式中A为沙纹床面的水平面积．图 6为形状摩阻系数的历时曲线，图7显示了振荡周期中各相位时刻沙纹附近无量纲压力的分布云图．将图 7中由左向右方向记为振荡流的正向流动方向，由右向左为反向．在自由流向正向转向时刻，如图 7(a)，沙纹背流侧上方存在较大的负压区，该负压区是由脱离沙纹表面的涡旋运动至该位置造成的．由于该涡旋已经不与床面接触，因此基本没有对床面压力产生影响.在自由流向正向加速阶段，如图 7(b)，沙纹所受正向压力的范围从沙纹顶峰到前一个沙纹背流侧坡面底部，而从顶峰到背流侧坡面中部，流动分离产生的涡旋对该段沙纹表面造成负压作用，沙纹所受压力的水平合力，即形状拖曳力符号为正．在自由流流速达到幅值的时刻，如图 7(c)，沙纹迎流侧坡面所受正压的范围和大小均有所减少．在自由流速减速时刻，如图 7(d)，受涡旋影响的负压区已经脱离沙纹表面，没有对床面产生作用，同时由于底部流速已经提前于自由流流速接近为 0，在沙纹迎流侧坡面没有造成正压作用，因此tw=135°时刻沙纹两侧压力差接近为0．由于流动分离、涡旋发展，导致沙纹两侧存在随相位变化的压力差，这是产生床面形状拖曳力的直接原因，也是影响床面总拖曳力的重要因素之一．

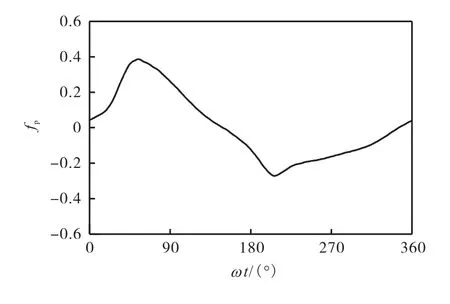
图6 形状摩阻系数历时曲线Fig.6 Time serials of form friction factor

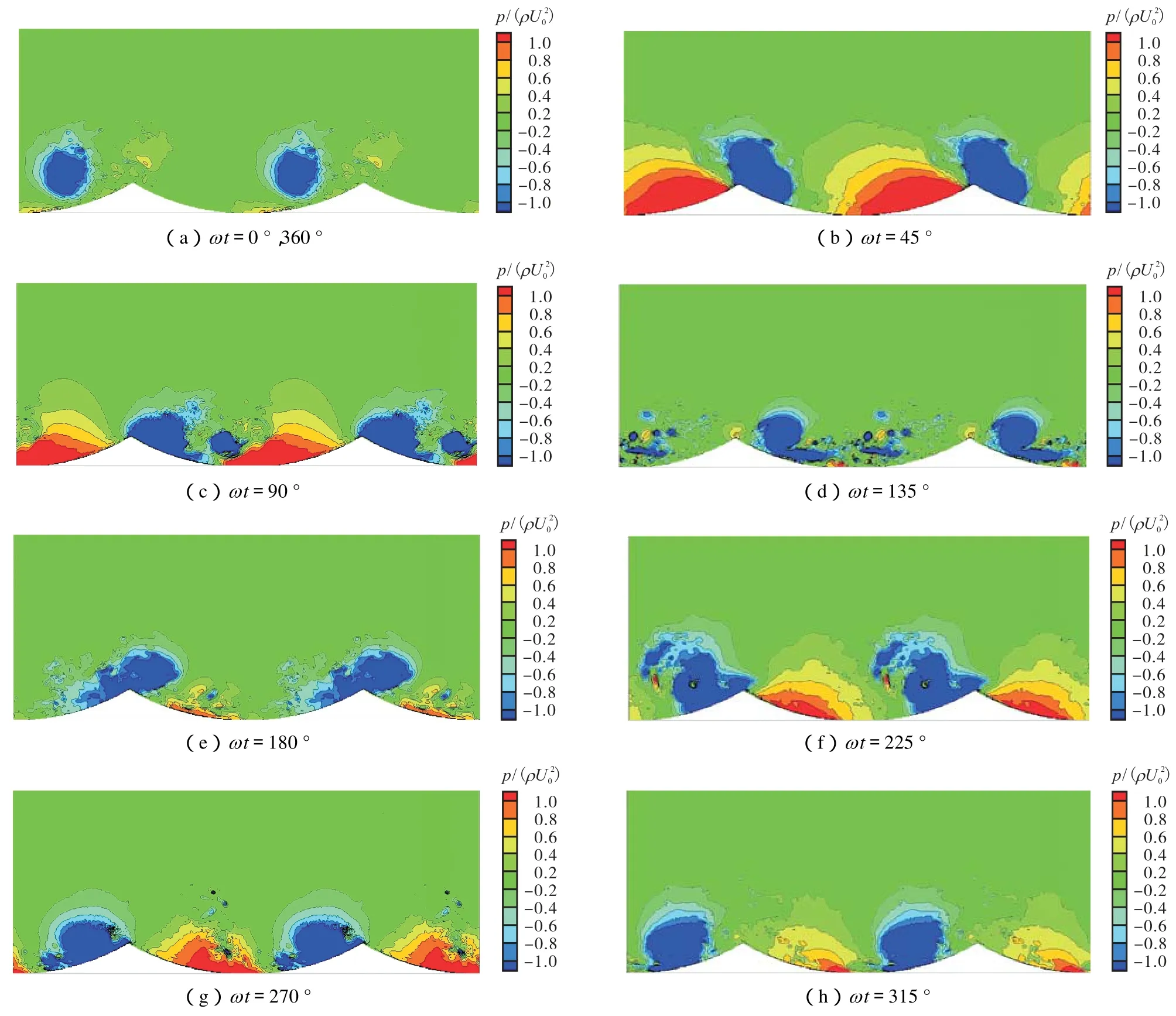
图7 各时刻压力场云图Fig.7 Pressure contour at different time series

3.4 沙纹床面受力

沙纹床面受到水平方向的总摩阻力FD包括两部分作用，分别是肤面摩阻力fF和形状摩阻力Fp．其中肤面摩阻力fF为沙纹表面肤面摩阻的水平方向分量的积分，常用无量纲的肤面摩阻系数衡量fF的大小，表达式为

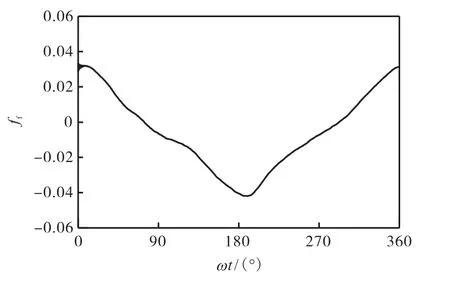
图8 肤面摩阻系数历时曲线Fig.8 Time serials of skin friction factor

图 8为肤面摩阻系数的历时曲线．表1中列出了本节验证算例和 Dimas等[28]算例的参数和作用力系数的结果．需要说明的是，DK算例沙纹坡度为0.14°，略小于本文的 0.159．从结果可见，本文与 DK的肤面摩阻系数ff分别为 0.04和 0.03，较为接近．本文形状摩阻系数的最大值fp,m为 0.39，略大于DK结果 0.34，可能的原因是本文算例的沙纹坡度为0.159，大于 DK 算例的 0.140，文献曾指出形状摩阻会随沙纹坡度增大而增大[29]，因此结果较合理．本文与 DK算例形状摩阻系数与肤面摩阻系数之比分别为9.8和11.3，证明在该条件下形状摩阻的作用远大于肤面摩阻，与文献中的结论相符[30]．由上述比较可知，通过本文的三维LB模拟可以得到比较合理的沙纹床面形状摩阻和肤面摩阻结果．

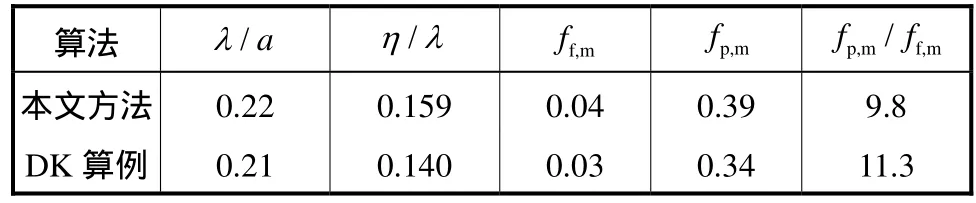
表1 摩阻系数与前人数模结果的比较Tab.1 Fiction factor result compared with numerical simulation result from literature

3.5 三维涡动力特性

图 9展示了振荡周期内时刻沙纹上的涡结构．图中的涡旋结构采用等值面识别[31]．在时刻，即图 9(a)、(b)所示，自由流流速处于正向加速阶段，沙纹顶峰背后已经发生流动分离，在顶峰背后形成沿z轴方向接近二维的滚动涡旋，并向下游运动．在时刻，即图 9(c)、(d)所示，自由流流速达到幅值，床面上的涡旋结构经过相互作用和与床面的作用，横向滚动涡已经分裂成大量小尺度的涡旋结构，在沙纹谷底上方，存在尺度相对较大的纵向涡结构，而此时涡旋还没有运动至下一个沙纹的迎流侧坡面．横向滚动涡出现在沙纹顶峰之后，沿着背浪面发展，一般存在于周期中加速相位的前期．横向滚动涡旋的出现，使靠近沙纹顶峰位置的床面切应力增大．图 10所示为在沙纹顶峰下游方向位置肤面摩阻系数的历时曲线．在时刻出现切应力幅值，与横向滚动涡出现的空间和时间对应．纵向涡主要出现在沙纹背流侧坡面和谷底上方，一般存在于加速阶段的后期一直到流动转向．图11所示为距离沙纹顶峰位置处肤面摩阻系数的历时曲线．可以看到在区间肤面摩阻系数从0.03变到－0.05，负向的肤面摩阻系数幅值一直持续到左右时刻，该段变化与纵向涡出现的空间和时间对应．

图9 沙纹床面上的典型涡结构Fig.9 Typical vortex structure over rippled bed

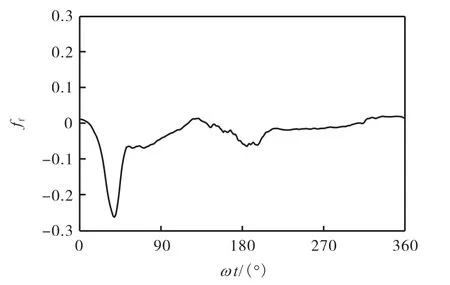
图10 /12位置肤面摩阻系数历时曲线Fig.10 Time series of skin friction factor at/12

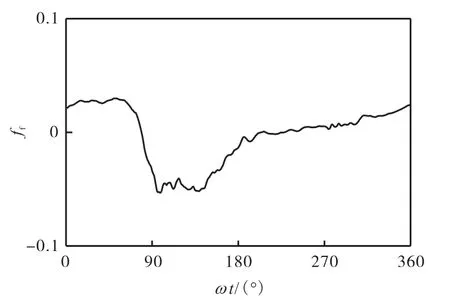
图11 /3位置肤面摩阻系数历时曲线Fig.11 Time series of skin friction factor at/3

4 结 语

将 WALE模型引入三维 LB模型，对沙纹床面上的振荡紊流流边界层进行了模拟，得到了与实验符合较好的水动力特性结果．比较Smagorinsky模型和WALE模型的模拟结果可知，在沙纹床面的模拟中，WALE模型可以更好地反映振荡流作用下的紊动强度等粗糙紊流特性．WALE模型与LB模型相结合计算得到的床面形状摩阻系数和肤面摩阻系数结果也与前人数模结果符合较好．计算结果还表明，在沙纹床面的情况下，床面总摩阻力中形状摩阻相对肤面摩阻占主要部分，与以往的结论一致．三维模拟还得到了沙纹上不同时刻出现的横向滚动涡和纵向涡结构及与肤面摩阻系数变化的关系．以上结果表明，所建立的结合 WALE大涡模拟模型的三维LB模型可以获得合理的沙纹床面振荡流边界层水动力和床面受力结果，可以利用该模型对沙纹床面振荡流粗糙紊流边界层运动特性进行系统研究，并进一步获得有关沙纹表观粗糙度和摩阻系数等的变化规,．

[1] Fredsøe J，Andersen K H，Sumer B M.Wave plus current over a ripple-covered bed[J].Coastal Engineering，1999，38(4)：177-221.

[2] Hare J，Hay A E，Zedel L，et al.Observations of the space-time structure of flow，turbulence，and stress over orbital-scale ripples[J].Journal of Geophysical Research，2014，119(3)：1876-1898.

[3] van der Werf J J，Magar V，Malarkey J，et al.2DV modelling of sediment transport processes over full-scale ripples in regular asymmetric oscillatory flow[J].Continental Shelf Research，2008，28(8)：1040-1056.

[4] 蒋昌波，白玉川，赵子丹，等.波浪作用下沙纹床面底层流动特性研究[J].水科学进展，2003，14(3)：333-340.

Jiang Changbo，Bai Yuchuan，Zhao Zidan，et al.Study on wave bottom boundary layers over a rippled bed[J].Advances in Water Science，2003，14(3)：333-340(in Chinese).

[5] 蒋昌波，白玉川，赵子丹，等.波浪作用下涡动沙纹床面的悬沙运动数值研究[J].水利学报，2003(3)：93-97.

Jiang Changbo，Bai Yuchuan，Zhao Zidan，et al.Numerical study on suspended sediment movement in wave boundary layers over rippled bed[J].Journal of Hydraulic Engineering，2003(3)：93-97(in Chinese).

[6] 蒋昌波，白玉川，赵子丹，等.沙纹床面上波流共同作用的数值模拟[J].水利学报，2005，36(1)：62-68.

Jiang Changbo，Bai Yuchuan，Zhao Zidan，et al.Numerical simulation for joint action of wave and current on rippled sea bed[J].Journal of Hydraulic Engineering，2005，36(1)：62-68(in Chinese).

[7] 程永舟，王永学，蒋昌波.非线性波作用下非对称沙纹床面流场特性数值分析[J].大连理工大学学报，2008，48(3)：423-429.

Cheng Yongzhou，Wang Yongxue，Jiang Changbo.Numerical analysis of characteristics of fluid field over asymmetric rippled bed under nonlinear wave[J].Journal of Dalian University of Technology，2008，48(3)：423-429(in Chinese).

[8] Barr B C，Slinn D N，Pierro T，et al.Numerical simulation of turbulent，oscillatory flow over sand ripples[J].Journal of Geophysical Research，2004，109：C09009-1-19.

[9] Grigoriadis D G E，Balaras E，Dimas A A.Coherent structures in oscillating turbulent boundary layers over a fixed rippled bed[J].Flow，Turbulence and Combustion，2013，91(3)：565-585.

[10] Zhang Q H，Sun Y B，Zhang J F.Simulation of oscillatory laminar boundary layer flow via the lattice Boltzmann method[C]// Proceedings of 3rd Internatioal Conference on Asian and Pacific Coasts.Jeju，Korea，2005：271-274.

[11] 孙亚斌，张庆河，张金凤.振荡层流边界层运动的格子Boltzmann模拟[J].水动力学研究与进展，2006，21(3)：347-353.

Sun Yabin，Zhang Qinghe，Zhang Jinfeng.Simulation of oscillatory laminar boundary layer flow based on lattice Boltzmann method[J].Journal of Hydrodynamics，2006，21(3)：347-353(in Chinese).

[12] Cappietti L，Chopard B.A lattice Boltzmann study of the 2D boundary layer created by an oscillating plate[J].International Journal of Modern Physics C，2006，17(1)：39-52.

[13] 丁 磊，张庆河.振荡流边界层中颗粒受力的三维格子玻耳兹曼模拟[J].水动力学研究与进展，2010，25(3)：391-397.

Ding Lei，Zhang Qinghe.3D lattice Boltzmann simulation of forces on a fixed spherical[J].Journal of Hydrodynamics，2010，25(3)：391-397(in Chinese).

[14] Ding L，Zhang Q H.Lattice Boltzmann simulation to characterize roughness effects of oscillatory boundary layer flow over a rough bed[C]//Proceedings of 32nd Conference on Coastal Engineering.Shanghai，China，2010：1397-1407.

[15] 周志博，张庆河.粗糙床面振荡紊流边界层运动的三维格子玻尔兹曼模拟[J].水动力学研究与进展，2016，31(4)：463-471.

Zhou Zhibo，Zhang Qinghe.3-D lattice Boltzmann simulation of turbulent oscillatory boundary layer flow over rough beds[J].Chinese Journal of Hydrodynamics，2016，31(4)：463-471(in Chinese).

[16] Nicoud F，Ducros F.Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J].Flow，Turbulence and Combustion，1999，62(3)：183-200.

[17] Weickert M，Teike G，Schmidt O，et al.Investigation of the LES WALE turbulence model within the lattice Boltzmann framework[J].Computers & Mathematics with Applications，2010，59(7)：2200-2214.

[18] Qian Y H，d'Humières D，Lallemand P.Lattice BGK models for navier-stokes equation[J].Europhysics Letters，1992，17(6)：479-484.

[19] Bhatnagar P L，Gross E P，Krook M.A model for collision processes in gases[J].Physical Review，1954，94：511-524.

[20] d'Humieres D.Generalized lattice-Boltzmann equations[C]//Rarefied Gas Dynamics：Theory and Simulations.Washington，USA，1992：450-458.

[21] Lallemand P，Luo L S.Theory of the lattice Boltzmann method：Dispersion，dissipation，isotropy，Galilean invariance，and stability[J].Physical Review E，2000，61(6)：6546-6562.

[22] Ladd A J C，Verberg R.Lattice-Boltzmann simulations of particle-fluid suspensions[J].Journal of Statistical Physics，2001，104(5/6)：1191-1251.

[23] He X，Zou Q，Luo L S，et al.Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model[J].Journal of Statistical Physics，1997，87(1/2)：115-136.

[24] Nguyen N Q，Ladd A J C.Sedimentation of hard-sphere suspensions at low Reynolds number[J].Journal of Fluid Mechanics，2005，525：73-104.

[25] Ladd A J C.Numerical simulations of particulate suspensions via a discretized Boltzmann equation(Part 1)：Theoretical foundation[J].Journal of Fluid Mechanics，1994，271：285-309.

[26] 崔桂香，许春晓，张兆顺.湍流大涡数值模拟进展[J].空气动力学学报，2004，22(2)：121-129.

Cui Guixiang，Xu Chunxiao，Zhang Zhaoshun.Progress in large eddy simulation of turbulent flows[J].Acta Aerodynamica Sinica，2004，22(2)：121-129(in Chinese).

[27] Temmerman L，Leschziner M A，Mellen C P，et al.Investigation of wall-function approximations and subgrid-scale models in large eddy simulation of separated flow in a channel with streamwise periodic constrictions[J].International Journal of Heat and Fluid Flow，2003，24(2)：157-180.

[28] Dimas A A，Kolokythas G A.Flow dynamics and bed resistance of wave propagation over bed ripples[J].Journal of Waterway，Port，Coastal，and Ocean Engineering，2011，137(2)：64-74.

[29] Kim H.Effective form roughness of ripples for waves[J].Journal of Coastal Research，2004，20(3)：731-738.

[30] Wikramanayake P N，Madsen O S.Calculation of Movable Bed Friction Factors[M].McNair E C，Russell K T.Dredging Research Program.Vicksburg：Army Corps of Engineers：1994：1-104.

[31] Jeong J，Hussain F.On the identification of a vortex[J].Journal of Fluid Mechanics，1995，285：69-94.