不规则细砂的统计特性及二维/三维数值模拟
2019-02-13王华昆余建星谭玉娜李修波冯志强
王华昆 ,余建星 ,余 杨 ,谭玉娜 ,李修波 ,冯志强
(1.水利工程仿真与安全国家重点实验室(天津大学),天津 300072;2.高新船舶与深海开发装备协同创新中心,上海 200240;3.钦州学院机械与船舶海洋工程学院,钦州 535011)
管道结构是深海油气运输的主要方式.由于油气开采中往往混杂大量的酸性气体(CO2,H2S)和水,形成腐蚀性环境,此外还夹杂沥青和固体砂粒,属于多相流动[1],在此条件下往往造成严重的冲刷腐蚀.冲刷腐蚀过程中,固体颗粒的侵蚀是造成损伤的主要原因.
在含固体颗粒的油气运输过程中管道弯管处的冲刷腐蚀尤为严重.目前,国外研究结构冲刷腐蚀或侵蚀的主要有 Tulsa大学的 Vieira等[2-3]、Arabnejad等[4]、Tian 等[5]和 Cheng 等[6]、Takaffoli 等[7-8]及Hadavi等[9-10].通过将回流式的全管冲刷腐蚀试验与计算流体动力学 CFD 相结合,Shirazi等[4]研究了颗粒属性、流动状态、流动介质等参数对弯管冲刷腐蚀的影响.在数值模拟过程中,假定颗粒为球形颗粒,通过单向或双向耦合的方式考虑颗粒与流体之间的相互作用.并结合由试验得到的经验或半经验侵蚀公式预测弯管侵蚀损伤及其损伤分布.Tian等[5]和Cheng等[6]采用旋转圆盘电极技术(RDE)定性研究多相流对冲刷腐蚀的影响.研究表明:油的存在会使钢表面形成一层油膜,促进了氧的阴极还原并阻碍了钢的溶解.随着溶液含砂量和砂粒大小的增大,钢的腐蚀增强[5],但文中并未给出砂粒的统计参数和形貌特征.而 Takaffoli等[7-8]和Hadavi等[9]结合试验和数值模拟重点研究颗粒侵蚀机理和侵蚀过程中靶材的响应以及颗粒形貌分析及有限元模拟方法.其中颗粒被简化为具有均匀厚度的六面体,该数值模型有明显的锐角,且不能模拟向内凹陷的曲面,与实际不符.Hadavi等[10]根据试验结果考虑了更真实的颗粒形状对撞击过程中颗粒破碎的影响.但颗粒轮廓需要通过试验参数导入,且模型依然采用等厚度假设.De Pellegrin等[11]开发了一种模拟具有随机凸多面体的磨料颗粒方法.这些随机多面体由平面切割一个立方体得到,平面的方向和位置分布是随机的.需要指出的是该模型无法模拟含有凹面的多面体,也未将模拟颗粒的统计参数与实际颗粒统计参数做对比.
目前,国内研究冲刷腐蚀的文献相对较少.刘海笑等[12-13]采用数值模拟方法分析不同侵蚀公式对弯管侵蚀损伤预测的适用性,研究表明 Tabakoff 的侵蚀公式具有较高的精度和较好的适用范围.卢宇辉等[14-15]则采用CFD模拟研究了通海截止阀的冲刷腐蚀行为.张政等[16]同样采用数值模拟方法,考虑了侵蚀过程中的流固双向耦合作用,分析了突扩圆管在固液两相流中的冲刷腐蚀.但以上研究均未分析实际的颗粒侵蚀过程,颗粒形状参数对侵蚀过程的影响仅采用形状因子等效考虑.
尽管 Papini等[7-9]对颗粒侵蚀做了较为详细的微观统计分析,但用四边形以及等厚度的板状三维实体模型模拟 SiC颗粒过于简化[7-8],此外管道多相流中携带的颗粒多为天然砂粒(SiO2),其材料属性与碳化硅(SiC)有较大差异.对于颗粒在侵蚀过程中的损伤分析,Papini等[10]基于试验测量得到SiC颗粒形貌数据,通过拉伸生成厚度均匀的板状数值模型,对实际做极大简化.此外,其他考虑流体作用的冲刷腐蚀研究[2-6,12-16]则几乎全采用宏观的侵蚀方程进行损伤分布和损伤大小预测,并用形状因子描述颗粒尖锐程度对侵蚀影响,而未考虑实际颗粒形貌和侵蚀过程.
针对已有砂粒数值模型过于简化及在只有砂粒分布参数条件下如何快速建立符合实际的砂粒有限元模型,本文提出新的二维、三维砂粒模型的构建方法.基于天然石英砂(SiO2)微粒 SEM 检测结果,结合图像处理技术,通过统计分析方法获取石英砂颗粒特征参数的分布类型及分布参数.并通过编程实现简化颗粒模型的数值重构.通过增加控制点数量,实现几何形状更复杂的颗粒模拟.此外,新模型考虑了颗粒分布参数之间的内在联系.将重构模型的特征参数与试验数据对比验证模型准确性后,结合用户自定义的 Python程序,将不规则砂粒模型嵌入通用有限元软件 ABAQUS,实现了不同类型砂粒的有限元模型重构,为砂粒冲刷腐蚀数值模拟研究提供依据.
1 试 验
试样为 6号(40~80目,0.2~0.5mm)天然石英砂颗粒.为建立合理的不规则石英砂颗粒的有限元模型,首先需获取颗粒的特征参数统计分布.将石英砂颗粒表面喷金处理后,采用 SEM 进行检测,检测结果如图1(a)所示.
为便于对石英砂颗粒进行形貌分析,首先将SEM 扫描图片转化为二值图,如图 1(b)所示,并用Photoshop提取颗粒轮廓(仅提取轮廓清晰的图像).根据 SEM 扫描图对应的标尺,将所有样本处理成1mm×1mm的黑底图片,每个图片包含一个颗粒,共 418个样本.通过 Matlab编程逐个提取颗粒形貌信息并存储,最后汇总进行统计分析.其中面积参数采用“regionprops”函数提取,等效直径(D)和颗粒纵横比(aspect ratio,AR)定义为

式中:A为石英砂颗粒平面投影面积;Lmaj为等效椭圆主轴长;Lmin为等效椭圆短轴长.等效椭圆定义为与颗粒平面投影形状具有相同二阶矩的椭圆.

图1 SEM检测结果及相应二值图Fig.1 Testing result of SEM and the corresponding binary image
颗粒特征参数统计分布及对应的不同分布函数拟合优度对比结果如图 2所示.结果表明:对数正态(lognormal)和广义极值(GEV)分布都能较准确地描述砂粒周长p、平面投影面积A、等效直径D、等效椭圆主轴长Lmaj和短轴长Lmin的分布类型,而纵横比(AR)则服从GEV分布.该结果与Papini等[9]给出的SiC颗粒检测结果有略微不同,后者表明粒子的面积服从 Gaussian分布,而D服从 Weibull分布[7-9].实际上 Weibull分布是 GEV分布的特殊情况,因此D也服从GEV分布.采用Gaussian分布描述颗粒面积的主要不足是:在蒙特卡洛(MCM)模拟过程中,模拟参数可能会出现负值,这与实际不符.因此,在模拟过程中往往需要对模拟值符号进行判断与限界,而采用对数正态分布可避免该问题.对数正态分布的概率密度函数为

其分布均值m和方差v可通过分布参数μ和σ得到.

由于GEV分布有3个分布参数,因此适用于分析复杂分布类型.GEV分布概率密度函数可表示为

式中:µ为位置参数;σ为尺度参数;k为形状参数.
对于,当k>0,对应Ⅱ型广义极值分布;当k<0,对应Ⅲ型广义极值分布;当k=0,对应Ⅰ型分布,即极值分布,此时对应概率密度函数为

由于GEV分布具有广泛适用性,因此采用GEV分布对各分布参数的试验统计数据进行拟合.对应的分布参数如表1所示.
实际上颗粒分布参数之间并非相互独立,面积A和周长p都依赖于颗粒的长、短轴.根据试验检测结果,通过非线性回归分析得到A和p与颗粒的长、短轴之间的关系如式(6)所示.解析函数与试验对比结果及对应的拟合优度参数见图3.图4给出了解析公式预测值与试验结果对比的误差分布及采用GEV分布拟合得到的回归参数.结果表明:该经验公式预测值与试验结果吻合良好,大部分误差均在±5%以内,且GEV分布可准确拟合误差分布.图5给出了考虑拟合误差和不考虑拟合误差的模拟结果对比.结果表明二者预测值差异很小.


图2 SiO2颗粒特征参数统计分布Fig.2 Statistical distribution of particle characteristic parameters of SiO2particles

表1 石英砂颗粒特征分布参数Tab.1 Characteristic distribution parameters of the silica sand particles

图3 SiO2颗粒特征参数相关性Fig.3 Inherent relationship between the distribution parameters of SiO2particles
在 Takaffoli等[7]的研究中,并未考虑颗粒面积、周长与颗粒长短轴之间的内在联系,也未考虑颗粒纵横比应满足的关系.仅通过球度参数(S=4πA/p2)考虑面积、面积与周长之间的关系,这种约束是偏弱的.实际上纵横比是颗粒的主要特征,该参数决定了颗粒是条状还是近似为方形.针对以上不足,本文模型通过考虑分布参数之间的内在联系,使得颗粒形状更加合理.并通过增加控制点数量实现更复杂几何形状的模拟.数值模拟方法见第2节.

图4 回归分析误差分布Fig.4 Error distribution of regression analyis

图5 考虑和不考虑拟合误差的模拟结果对比Fig.5 Comparison of the simulation results with and without the consideration of regression error
2 二维数值模拟与验证
根据第1节试验统计分析结果,采用Matlab编程实现平面颗粒模型二维重构.采用8顶点模型模拟颗粒平面投影形状,并根据颗粒厚度分布随机数控制三维简化模型(见第 3节).二维数值模型模拟过程如下.
步骤 1 根据表 1主轴长和纵横比满足的分布类型及对应的分布参数,采用 MCM 随机生成样本Lmaj、AR,从而确定短轴长Lmin=Lmaj/AR;
步骤 2 结合式(6)的回归分析结果,根据主轴、短轴长确定颗粒面积(A0),考虑回归分析的误差分布(图 4(a)),采用 MCM 得到面积预测误差样本ErrorA,从而确定实际用于模拟的颗粒面积Ac=A0(1+ErrorA);
步骤 3 假设极径Ri和极角θi均满足均匀分布,采用MCM随机生成样本Ri和θi(图6(a)),从而确定象限Ⅰ~Ⅳ4个顶点的X、Y坐标(Pi表示顶点P编号,见图 6(b)),各参数计算方法及对应参数范围如式(7)所示.4个顶点坐标信息均在象限Ⅰ中生成,然后变换至其他象限.θmin表示控制点P与原点O构成的直线与横轴之间夹角的最小容许值.
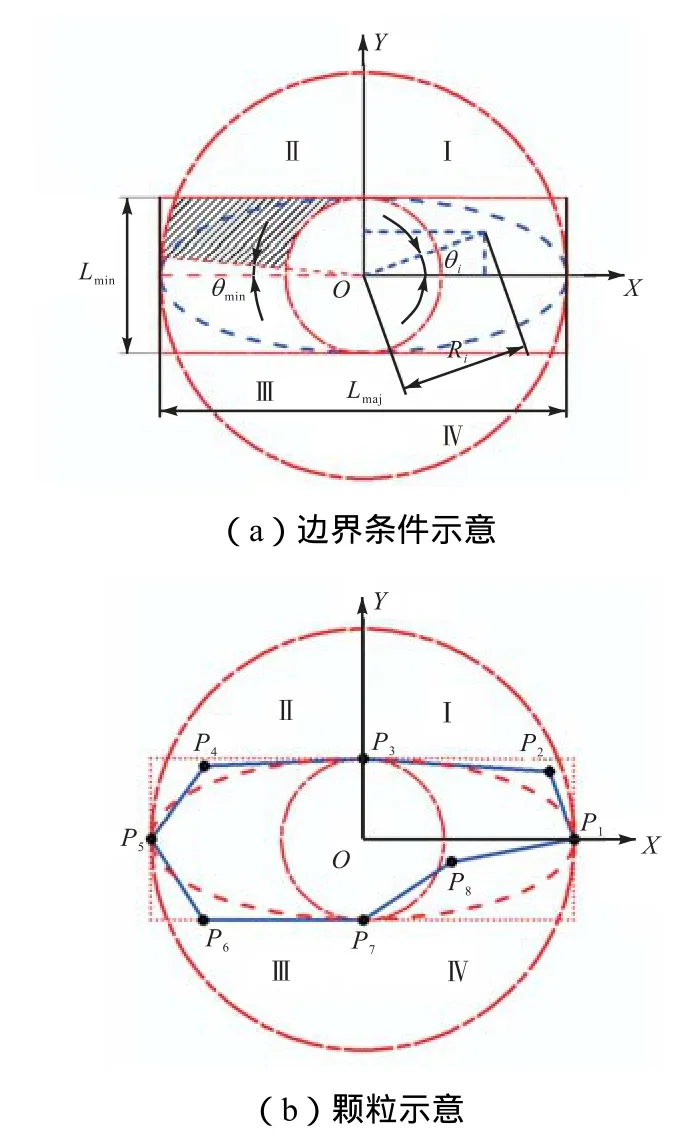
图6 数值模型示意Fig.6 Schematic of the numerical model

步骤 4 根据颗粒面积Ac、8个顶点(P1~P8)的X坐标以及前7个顶点(P1~P7)的Y坐标,重置第8个顶点的Y坐标.
步骤5 计算颗粒顶点3-8间距(L38)、4-8(L48)、5-8(L58)及颗粒周长,判断实际周长与回归函数预测值(图 3(b))之间的误差是否落在周长误差范围内,若不满足则返回步骤3.根据所要模拟的颗粒数N重复步骤1~5.
图 7为生成数值模型的模拟流程.注意:顶点P1、P3、P5和P8在步骤 1确定等效椭圆长、短轴时已完全确定.图 6(a)中的阴影区域为顶点控制域(用于象限Ⅰ、Ⅱ、Ⅲ),象限Ⅳ施加的边界条件为顶点 3-8、4-8、5-8之间的距离小于主轴长,从而保证颗粒的纵横比不变.极角,以保证颗粒不出现极其尖锐的顶点(本文取).试验检测结果表明:石英砂颗粒并无特别尖锐的角点,在第 3节有限元模型中将通过增加圆角进一步改进.
ABAQUS 的内核语言是 Python语言,由于Python中没有可生成满足 GEV分布的内置随机函数,因此,通过求累积分布函数F(x)的逆函数得到纵横比样本x.此外,也可直接将Matlab生成的几何参数直接写入.py文件,进行参数化建模.给定频率y的GEV分布逆函数可表示为

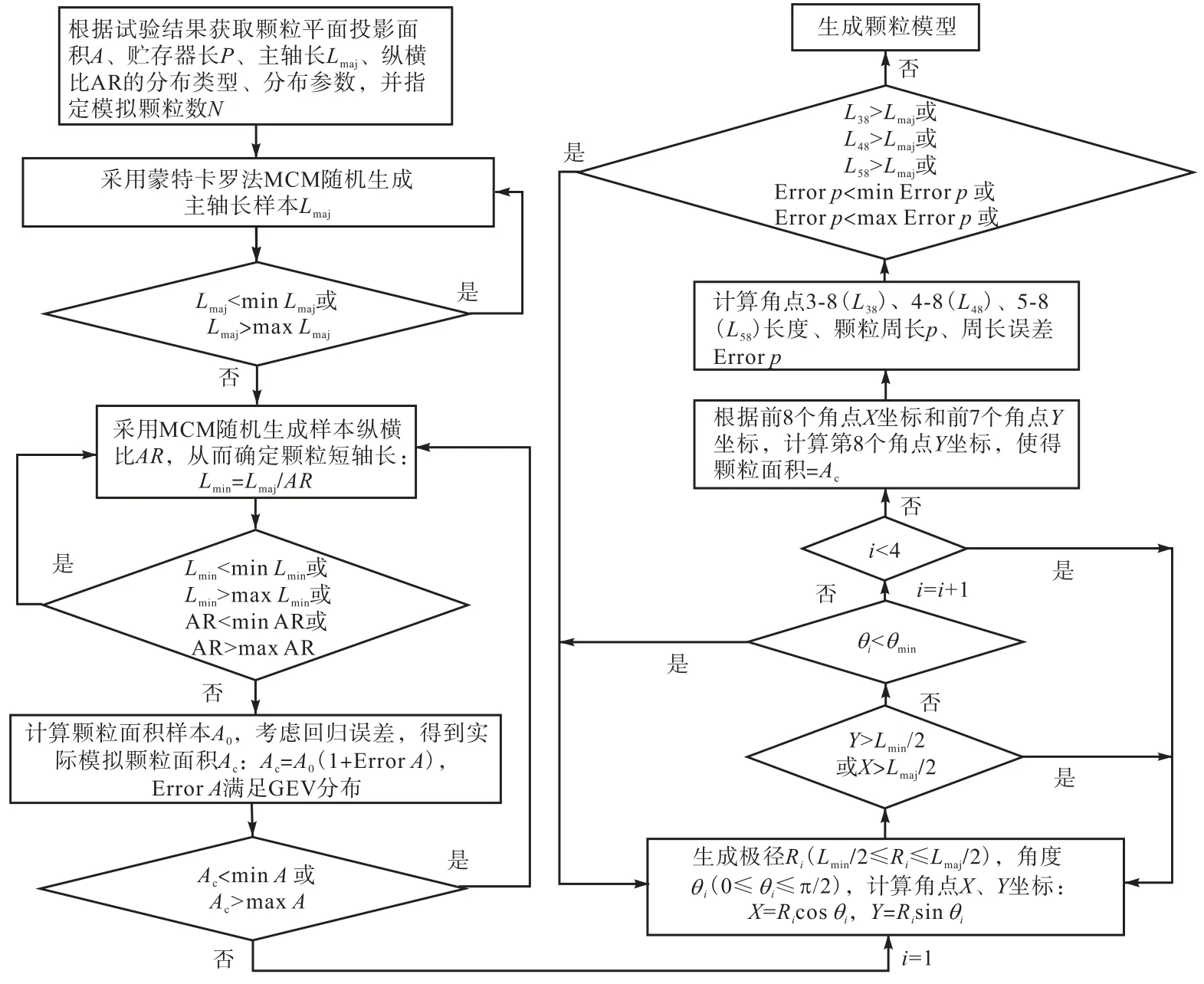
图7 二维模型数值模拟流程Fig.7 Flow chart of the numerical simulation of two-dimensional particle
图8为试验结果与数值模型特征参数的对比,相应的典型二维数值模拟结果如图 9所示.研究表明:数值模型不仅保证颗粒的纵横比一致,其颗粒面积、颗粒周长对应的分布与试验结果吻合良好,表明该数值算法是可靠的.第 3节将基于该二维平面模型建立三维有限元模型.

图8 2D模型验证Fig.8 Validation of two-dimensional model

图9 数值模拟二维粒子几何形状Fig.9 Simulation results of the two-dimensional particles
3 三维模型有限元模拟
二维模型常常作为三维模型的简化,第2节通过数值模拟已得到合理的不规则砂粒平面投影二维模型.颗粒形状是影响侵蚀过程的主要因素之一,不同的颗粒形状引起的侵蚀机理也不同:对于尖锐粒子来说,主要观察到韧性侵蚀,而在球状颗粒中观察到脆性侵蚀.此外,有角颗粒会嵌入基体材料,而球形粒子一般不会[17].由于砂粒形状会影响侵蚀机理从而影响侵蚀过程,因此,建立砂粒的三维随机模型对砂粒侵蚀机理研究具有重要的意义.
图1的颗粒形貌SEM检测结果表明:石英砂颗粒包含片状、单向平面状和一般不规则形状.假定SiO2颗粒的厚度和 SiC颗粒厚度一样均服从对数正态分布[9].根据实际检测结果,将砂粒分为以下 3种简化模型:Model Ⅰ:等厚度片状模型;ModelⅡ:单向变壁厚模型;Model Ⅲ:双向变壁厚模型.Model Ⅱ和Model Ⅲ的构建是基于Model Ⅰ通过布尔切割运算实现的.根据第 2节的数值模拟算法,采用MCM模拟得到满足对数正态分布的颗粒厚度样本,通过自定义的 Python程序,采用“自顶向下”的方法通过布尔运算将随机颗粒模型在ABAQUS中重构,实现厚度不均颗粒的有限元模型构建.三维模型数值模拟流程如图10所示.其中:切割部件与某一边平行,夹角θj(θmin≤θj≤θmax)定义为切割面与竖轴之间的夹角,如图 11所示,图中阴影区为切割区域.

图10 三维模型数值模拟流程Fig.10 Flow chart of the numerical simulation of three-dimensional model
根据类型索引号(图9中i的值)按图10流程图生成不同类型的三维微粒模型.其中θmax不宜过大,否则会改变颗粒模型的最大厚度,导致砂粒厚度分布不满足既定分布,而θmin可不做限制,θmin=0表示不切割.切割深度h1和h2是随机确定的,计算方式为

式中:h为颗粒厚度且满足对数正态分布分布;Llow和Lup分别表示随机数下限和上限,一般取0和1.

图11 布尔切割运算示意Fig.11 Schematic of Boolean cutting operation
图 12(a)~(c)分别给出了 3种简化模型的几何模型和有限元模型.从左至右依次为一般模型、圆角模型和有限元模型.图 12(d)中给出的为全部施加圆角后的模型,在模拟过程中可根据模型几何边索引号(随机确定)对任意几何边进行不同圆角半径过渡,使数值模型更贴近实际.图 12(b)为单向变壁厚模型,图 12(c)为双向变壁厚模型,图 12(d)为典型的不同类型颗粒有限元模型.从图 12中可以看出该方法可得到任意几何形状的颗粒,后续将基于该颗粒模型展开深入的颗粒侵蚀机理分析.

图12 细砂颗粒三维数值模型Fig.12 Three-dimensional numerical model of fine sand particle
4 结 论
本文基于试验检测结果得到天然石英砂微粒(40~80目)特征参数的分布类型和对应的分布参数.根据试验结果提出一种新的二维、三维不规则颗粒模型模拟方法,得到如下结论.
(1) 砂粒周长p、平面投影面积A、等效直径D、等效椭圆主轴长Lmaj和短轴长Lmin服从 Lognormal或GEV分布,而纵横比AR则服从GEV分布.GEV分布具有最广泛的适用性,适用于描述复杂分布.
(2) 新数值方法通过考虑颗粒长短轴之间的比例关系以及面积、周长与长短轴之间的内在联系,使得数值模型更贴近实际.
(3) 基于二维模型建立的三维模型既保证平面特征参数的统计特性,又考虑了颗粒厚度分布.通过不同的简化模型,编程实现了不同类型石英砂微粒三维数值重构,通过圆角功能避免了不切实际的锐角,为管道的颗粒侵蚀损伤机理研究提供必要的信息.
[1] Ige O O,Umoru L E.Effects of shear stress on the erosion-corrosion behaviour of X-65 carbon steel:A combined mass-loss and profilometry study[J].Tribology International,2016,94(2):155-164.
[2] Vieira R E,Parsi Mazdak,Zahedi Peyman,et al.Sand erosion measurements under multiphase annular flow conditions in a horizontal-horizontal elbow[J].Powder Technology,2017,320:625-636.
[3] Vieira R E,Mansouri A,Mclaury B S,et al.Experimental and computational study of erosion in elbows due to sand particles in air flow[J].Powder Technology,2016,288:339-353.
[4] Arabnejad H,Shirazi S A,Mclaury B S,et al.The effect of erodent particle hardness on the erosion of stainless steel[J].Wear,2015,332/333:1098-1103.
[5] Tian B R,Cheng Y F.Electrochemical corrosion behavior of X-65 steel in the simulated oil sand slurry.Part I:Effects of hydrodynamic condition[J].Corrosion Science,2008,50(3):773-779.
[6] Tang X,Xu L Y,Cheng Y F.Electrochemical corrosion behavior of X-65 steel in the simulated oil-sand slurry.PartⅡ:Synergism of erosion and corrosion[J].Corrosion Science,2008,50(5):1469-1474.
[7] Takaffoli M,Papini M.Numerical simulation of solid particle impacts on Al6061-T6,Part I:Threedimensional representation of angular particles[J].Wear,2012,292/293(29):100-110.
[8] Takaffoli M,Papini M.Numerical simulation of solid particle impacts on Al6061-T6,Part Ⅱ:Materials removal mechanisms for impact of multiple angular particles[J].Wear,2012,296(1/2):648-655.
[9] Hadavi V,Michaelsen B,Papini M.Measurements and modeling of instantaneous particle orientation within abrasive air jets and implications for particle embedding[J].Wear,2015(336/337):9-20.
[10] Hadavi V,Moreno C E,Papini M.Numerical and experimental analysis of particle fracture during solid particle erosion,Part I:Modeling and experimental verification[J].Wear,2016(356/357):135-145.
[11] De Pellegrin D V,Stachowiak G W.Simulation of threedimensional abrasive particles[J].Wear,2005,258:208-216.
[12] 王思邈,刘海笑,张 日,等.海底管道沙粒侵蚀的数值模拟及侵蚀公式评价[J].海洋工程,2014,32(1):49-59.
Wang Simiao,Liu Haixiao,Zhang Ri,et al.Numerical simulations of sand erosion in pipelines and evaluations of solid particle erosion equations[J].The Ocean Engineering,2014,32(1):49-59(in Chinese).
[13] 张 日,刘海笑.流动保障中管道的颗粒侵蚀分析[J].海洋工程,2012,30(4):10-20.
Zhang Ri,Liu Haixiao.Solid particle erosion analysis of pipelines in flow assurance[J].The Ocean Engineering,2012,30(4):10-20(in Chinese).
[14] 卢宇辉,卢锐新,程千驹,等.影响通海截止阀冲刷腐蚀的重要参数数值模拟分析[J].应用科技,2016,43(4):70-75,80.
Lu Yuhui,Lu Ruixin,Cheng Qianju,et al.Numerical simulation and analysis of key parameters influencing the scouring corrosion of the deep diving cutoff valve[J].Applied Science and Technology.2016,43(4):70-75,80(in Chinese).
[15] 卢宇辉,卢锐新,刘少刚.通海截止阀冲刷腐蚀的数值模拟及优化[J].应用科技,2016,43(1):61-66.
Lu Yuhui,Lu Ruixin,Liu Shaogang.Numerical simulation and optimization for erosion corrosion of the cutoff valve[J].Applied Science and Technology,2016,43(1):61-66(in Chinese).
[16] 张 政,程学文,郑玉贵,等.突扩圆管内液固两相流冲刷腐蚀过程的数值模拟[J].腐蚀科学与防护技术,2001(2):89-95.
Zhang Zheng,Cheng Xuewen,Zheng Yugui,et al.Numerical simulation of errosion-corrosion in liquidsolid two-phase flow[J].Corrosion Science and Protection Technology,2001(2):89-95(in Chinese).
[17] Roy M,Tirupataiah Y,Sundararajan G.Effect of particle shape on the erosion of Cu and its alloys[J].Materials Science and Engineering:A,1993,165(1):51-63.
