石英纤维复合材料的磨削加工性能研究

王玉果，徐靖宇，林 彬

(天津大学先进陶瓷与加工技术教育部重点实验室，天津 300350)

复合材料是由两种或两种以上不同性质的材料，通过物理或化学的方法，在宏观和微观上组成具有新的物理或者化学性能的材料．陶瓷基机织复合材料因为其整体性好、可设计性强、强度高、耐高温、抗损伤性好、成本相对较低等优异特性，在国防科技和航空航天等高新技术领域中具有很大的发展潜力．

对于机织复合材料的细观结构和力学性能，国内外学者已有较多研究，陈凡军等[1]分析了三维角联锁机织复合材料的细观几何结构，将建立的几何模型导入有限元分析软件中对弹性模量进行了预测；董伟锋等[2]提出了一个新的2.5维机织物复合材料有限元模型，该模型较为真实地模拟了织物内纤维束的轮廓结构和走向，以机织结构和纤维束排列密度为参数，详细研究了对 2.5维机织复合材料弹性性能的影响情况；姚瑶等[3]研究了一种层层接结三维角联锁机织复合材料在三点弯曲交变循环载荷下的疲劳破坏与失效模式，破坏主要集中于经纱屈曲起伏的最大曲率区域．国外学者 Ko等[4]提出力学分析模型，假定细观结构中纱线为折线波纹状，经角度转换后得到组合的力学模型；Pochiraju等[5]通过建立几何模型描述机织结构中纤维分布情况，该模型将厚度方向上排列的纱线根数和纱线的几何尺寸作为结构参数，用正弦曲线来描述接结经轴线的几何形状，用直线表示纬纱和填充纱的轴线形状．

复合材料特殊的结构使实现复合材料的精密高效加工成为制造领域的难题．随着有限元技术的不断成熟，部分学者通过有限元的方法对复合材料的加工进行模拟研究，Wang等[6]对复合材料的磨削过程进行了有限元模拟分析，并进行了验证实验，发现经纱与纬纱间的界面破坏严重，在磨削过程中沿经纱向外延伸与实验结果吻合较好；路冬等[7]则将重点放在切削过程中基体破坏、基体损伤演化及亚表面损伤机制；高汉卿等[8]则是通过建立纤维、基体、界面等各个组成相独自的材料本构模型从而建立了多相态细观仿真切削模型；伯明翰大学的Abena等[9]对于切削正交碳纤维增强复合材料提出了一种新的界面模型；Solani等[10]则通过建立基于 Hashin强度准则的损伤演化模型，讨论了网格形状、数目等对所建立模型的损伤演化的影响；Rao等[11]建立了三维微观单向纤维增强复合材料有限元模型，其切屑仿真结果与实验结果很接近；Mahdi等[12]通过建立二维有限元切削模型研究了切削力随切削条件和材料各向异性的变化规律；李巾锭等[13]建立了单个磨粒磨削的模型，同时利用有限元手段可以对不同磨削条件下的情况进行仿真分析．

声发射(AE)技术因其能够动态检测损伤的发生、扩展及断裂过程得到广泛应用，通过对 AE信号的振铃计数、振幅、能量等进行分析，可以得到材料内部变化的相关信息[14].基体开裂产生的 AE信号具有低幅值、中等上升时间及中等持续时间，纤维断裂则产生高幅度、高能量和长持续时间的 AE信号[15]．AE信号的峰值频率与复合材料的损伤模式有对应关系，基体开裂对应低频率范围，纤维断裂对应高频率范围[16].

本文以浅交弯联机织复合材料为例建立了三维细观模型，利用有限元方法，首先从宏观的角度对材料进行单磨粒磨削仿真，再分别从微观的角度对不同的磨削方向进行模拟仿真，结合实验通过观察材料表面加工形貌以及通过声发射技术辨别材料损伤模式来对材料在不同磨削角度下的磨削性能进行了研究分析．

1 机织复合材料细观模型建模

1.1 机织复合材料结构

图1为浅交弯联机织复合材料实物图．如图所示，纬纱的纱线呈直线状态，经纱的纱线具有规律弯曲状态，在纬纱的长度方向上每两层经纱与纬纱交织一次，构成2.5维浅交弯联机织物．

图1 浅交弯联机织物实物图Fig.1 Shallow interlocking and intersecting woven composites

1.2 基于简化假设的几何模型建立

在建立机织复合材料模型前，针对复合材料进行适当简化假设[17]．

(1) 图2中的经纱横截面为矩形，纬纱横截面为双凸透镜形，纬纱轴线为直线，经纱轴线为曲线．

(2) 织物结构均匀，经纬纱排列规则、紧密，纱线截面积不变．

(3) 材料复合过程在理想条件下进行，纤维与树脂间的界面(由基体和增强相通过化学反应生成的一层结构复杂的物质)性能良好，树脂中没有裂痕、缺陷和气泡．

细观模型中对复合材料的各个组分(纤维、基体、界面层)单独建模，如图2所示．

图2 复合材料细观几何模型Fig.2 Meso-geometric model of composite materials

2 有限元模型及实验方案

2.1 材料参数

复合材料由黏结层、纤维束(经纱、纬纱)以及基体组成，其中纤维束为横观各向同性材料．纤维由石英纤维构成，基体由 SiO2基体构成，材料参数如表 1所示[18]．

表1 石英纤维和基体材料参数Tab.1 Material parameters of quartz fiber and matrix

2.2 材料本构模型及有限元设置

本文采用细观组分级的失效判据来模拟复合材料渐进损伤/失效的过程．对于纤维损伤，采用Hashin失效准则中纤维组分的失效判据，失效准则如下所述．

纤维拉伸失效，时：

纤维压缩失效，时：

纤维横向剪切损伤，时：

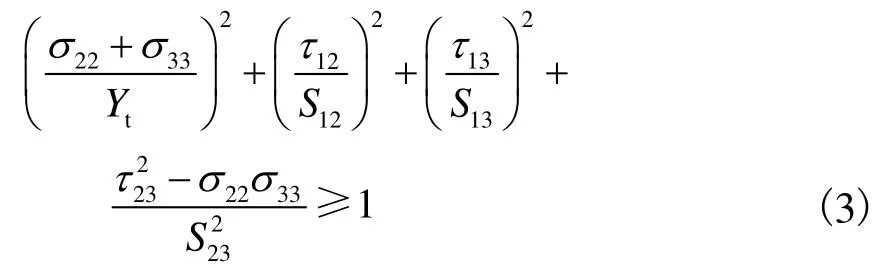
纤维横向剪切损伤，时：

基体采用最大应力准则．界面层采用基于牵引力-位移本构模型的 cohesive内聚力单元，采用二次应力失效作为损伤的起始准则，即

式中：t1、t2为面内剪应力；t3为法向拉伸应力；S、T、N分别为对应的损伤起始值．损伤起始后，界面损伤的扩展根据单元能量释放率来决定，采用损伤扩展准则(B-K准则)表征界面损伤扩展，即

在三维有限元模型中，选用六面体结构分网技术，单元类型选取C3D8R，即六结点线性六面体减缩积分单元，二维模型中，选用四边形自由进阶算法划分网格，单元类型选取 CPS4R，即四结点双线性平面应力四边形单元，用内聚力单元来模拟纤维基体间的界面层(cohesive)．磨粒进给速度为 8m/min，磨削深度为0.015mm．

2.3 磨削加工实验

为了验证上述仿真分析结果的准确性，通过数控光学曲线磨床MK9025来对石英纤维增强SiO2基机织复合材料进行磨削加工，磨削参数如表 2所示．通过扫描电镜来观察不同夹角的磨削加工的表面形貌特征，应用声发射(AE)技术实时监测材料损伤，并与仿真结果进行对比．

表2 实验参数Tab.2 Experimental parameters

3 结果分析与讨论

本文首先从整体上对石英纤维复合材料的磨削加工过程进行细观尺度模拟仿真，再分别从微观尺度建立三相(纤维-界面-基体)的几何模型，探究不同纤维方向角对复合材料磨削性能的影响，从材料细观尺度上的整体失效来推测材料微观尺度上的局部破坏，从微观尺度上通过实验与仿真结合讨论出材料磨削机理并与材料细观尺度上的整体失效相对应，进而能够更详实地讨论材料的磨削力、局部残余应力及磨削机理，为石英纤维复合材料的磨削机理研究提供一种新思路．

磨削加工其本质上仍属于切削加工，只不过是通过砂轮的磨粒、磨刃实现对工件表面进行加工的．在磨削过程中参加切削的磨粒数很多，但砂轮表面上磨粒的形状极不规则，参加切削工作的磨刃形状也是不确定的．砂轮中的磨料磨粒是不规则的多面体，磨粒在砂轮表面上的分布也是随机的，同时，由于磨粒在砂轮外圆周面上并不是等高地分布在同一外圆周上，因而砂轮表面上同时参加切削的有效磨粒数也是不确定的．为便于认识磨削过程与揭示磨削机制，本文利用SolidWorks中二次开发的Rnd函数生成多个随机平面，将磨粒切割成多面体，如图 3所示，对复合材料进行单磨粒磨削仿真．图 4为对所建的复合材料细观几何模型进行单磨粒磨削的仿真结果，在磨削过程中材料不断受到磨粒挤压、拉伸、弯曲、剪切的综合作用，切屑的形成为基体破坏和纤维断裂的结果，纤维周围的界面发生破坏并形成沟壑．

图3 磨粒几何模型Fig.3 Geometric model of abrasive particle

图4 复合材料细观几何模型的单磨粒仿真Fig.4 Single-abrasive particle simulation of composite microscopic geometric model

由于纤维增强复合材料是由两种不同的成分材料组成的，物理、力学性能相差较大，其磨削过程中的各种问题，如纤维拔出、折断等在很大程度上取决于磨削方向与纤维方向之间的关系．为探究纤维角度对磨削性能的影响规律，本文基于纤维-界面-基体的三相微观结构[19]，建立了二维微观有限元动态磨削模型，以 45°为增量，选取不同夹角q(0°、45°、90°、135°)对仿真结果进行分析，预测材料磨削过程中发生的损伤．

3.1 沿着纤维端面磨削

图 5所示为纤维端面的磨削仿真结果，其中 M代表基体，F代表纤维．图 6所示为通过实验获得的沿纤维端面磨削的表面形貌．图7所示为端面的声发射频谱及小波能量分布．

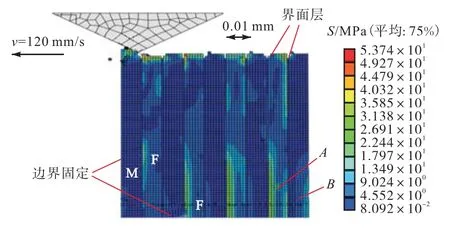
图5 沿着纤维端面的磨削仿真结果Fig.5 Grinding simulation results along the end of fiber

从图5可以看出，当磨削方向沿着纤维的端面磨削时，材料受到磨粒的挤压和剪切作用，当压缩应力超过基体的抗压强度时，基体发生破坏，引起基体和界面的碎裂和滑移，产生松散的切屑．当磨粒接触到纤维时，由于受到磨粒的挤压与剪切作用，在纤维内部产生垂直于纤维轴线的应力，从应力图中可看出端部纤维存在残余应力，当剪切应力超过纤维的剪切强度时，纤维被切断．界面的裂纹沿着纤维长度方向向下延伸，加工的表面较为平整，亚表面损伤的程度较轻，通过与实验获得的材料破坏形貌(如图6所示)比较可知，该方向的复合材料破坏模拟结果与实验结果吻合较好．

图6 沿纤维端面的磨削表面电镜图像Fig.6 Grinding surface SEM image along the end of fiber

从图 6中可以看出，沿着纤维断面磨削时，纤维断头主要受到砂轮磨粒的剪切作用，受剪切作用而断裂的断头端面呈平整型，有个别的纤维拔出现象发生．对应的AE信号如图7所示，AE信号集中在5～15kHz，材料在该频率段内主要发生基体破碎和界面剥离[20]，从声发射能量分布并不能看出有大量纤维断裂的迹象，其主要因为纤维受到剪切的作用，而纤维剪切模量较小，产生的AE信号在低频率段内与其他损伤模式混淆．在30～35Hz频率段内能看到纤维受拉而发生纤维拔出的断裂现象．

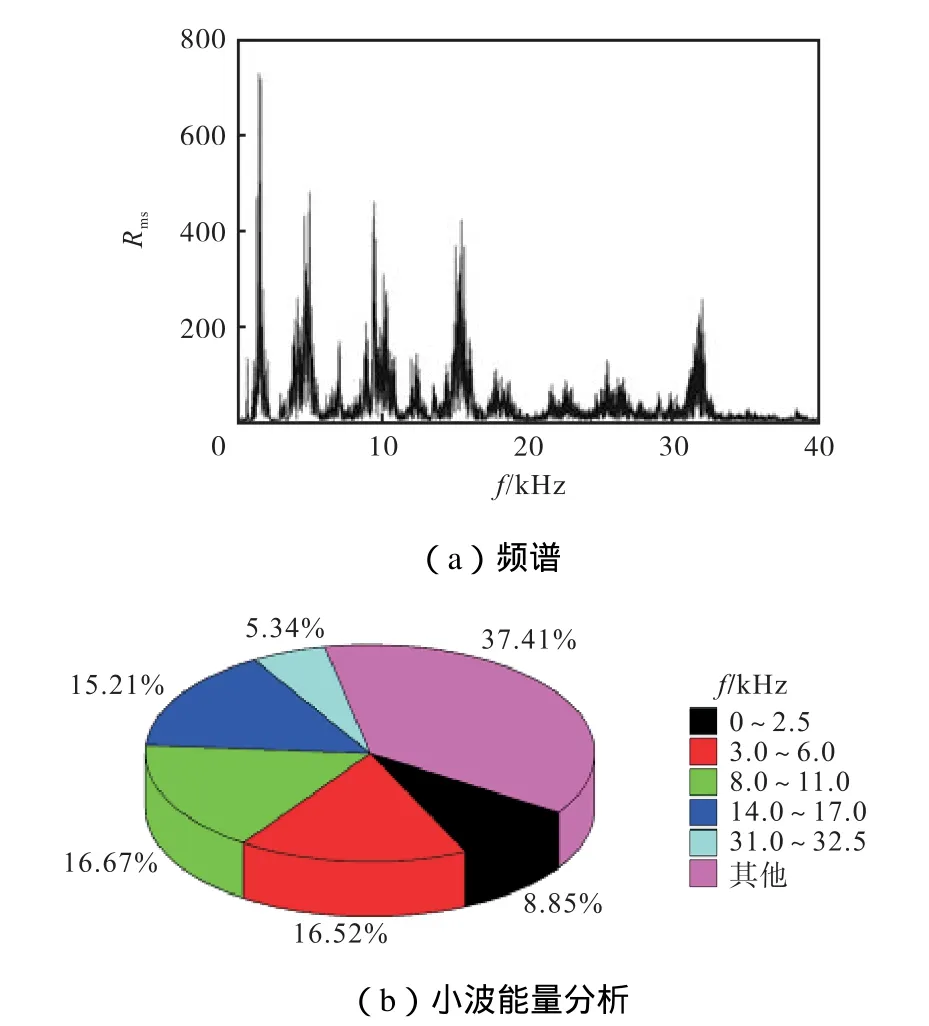
图7 声发射频谱及小波能量分布(端面)Fig.7 Spectrum and wavelet energy distribution map ofacoustic emission signal(end of filer)

3.2 磨削方向与纤维的夹角为0°

从图8可以看出，当磨削方向与纤维夹角为0°，即磨粒磨削方向平行于纤维方向时，随着刀具的进给，处于磨削部分的基体不断承受磨粒的挤压，基体由于受到磨粒的挤压作用发生断裂，界面失效产生裂纹，造成纤维基体间界面脱黏，纤维受到磨粒不断耕犁、挤压作用发生类似悬臂梁的弯曲变形，当纤维的弯曲应力到达抗弯强度时，纤维断裂．被加工的纤维表面凹凸不平；磨削加工的表面加工质量较差，处于亚表面的基体和界面发生损伤，亚表面的损伤程度较轻．

如图 9所示，加工后结果与仿真结果吻合较好，磨削表面出现了长度不一、参差不齐的纤维断头．这是由于纤维受到磨粒的挤压、弯曲的复合作用，纤维断裂随机分布．大部分基体破碎，产生的裂纹沿着基体与界面进行扩展，导致界面脱黏现象，部分纤维拔出，部分基体由于黏结剂的作用黏附于纤维周围．图10为该方向的声发射信号，信号在低频率段的能量值较大，材料主要发生纤维基体界面破坏以及基体破碎，纤维断裂的信号能量分布较少．

图8 磨削方向与纤维成0°时的磨削仿真结果Fig.8 Grinding simulation results when the angle between the grinding and fiber direction is 0°

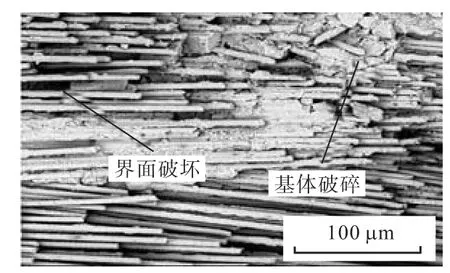
图9 磨削表面电镜图像(＝0°)Fig.9 SEM image of grinding surface(＝0°)

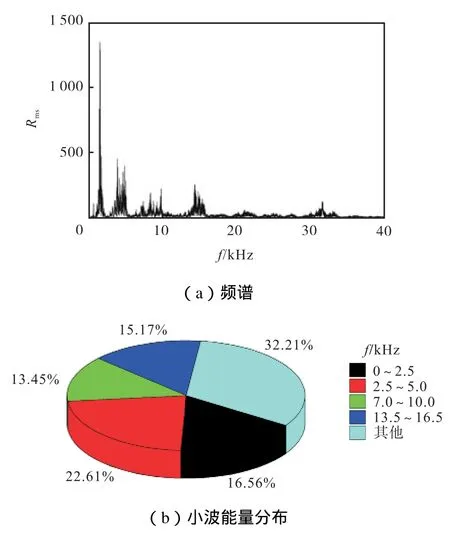
图10 声发射频谱及小波能量分布(＝0°)Fig.10 Spectrum and wavelet energy distribution map of acoustic emission signal(＝0°)

3.3 磨削方向与纤维的夹角为45°

如图 11所示，DMICRTMAX为一无量纲，用来表征材料发生的损伤，当磨削方向与纤维的夹角为45°时，与磨粒接触的材料达到压缩强度后，材料被压溃；在磨粒不断耕犁作用下，基体破碎，纤维发生断裂，形成非连续块状切屑；沿纤维长度方向界面脱黏的现象比较严重；亚表面损伤的程度并没有随着加工的进行而得到缓解．

材料加工后表面形貌如图 12所示，纤维受到挤压、弯曲的复合作用发生断裂、拔出，断头呈阶梯形，表面平整度一般．图 13是夹角为 45°时对应的 AE信号，AE信号能量值分布在25～35kHz频率段内较多，材料主要发生纤维断裂．通过磨削实验得到材料加工后的表面形貌和声发射结果与仿真有较好的对应关系．

图11 磨削方向与纤维成45°时的磨削仿真结果Fig.11 Grinding simulation results when the angle between the grinding and fiber direction is 45°

图12 磨削表面电镜图像(＝45°)Fig.12 SEM image of grinding surface(＝45°)

图13 声发射频谱及小波能量分布(＝45°)Fig.13 Spectrum and wavelet energy distribution map of acoustic emission signal(＝45°)

3.4 磨削方向与纤维的夹角为135°

从图 14可以看出，磨削加工后的复合材料表面同样凹凸不平，纤维在磨粒作用下先被掀起然后折断，断面并不齐整，并引起周围的界面开裂和基体破碎，形成凹坑；材料在磨粒挤压作用下沿界面开裂，裂纹沿着纤维长度方向向下延伸，并造成纤维、基体界面严重脱黏；亚表面损伤的程度较重，加工表面呈锯齿状．

图14 磨削方向与纤维成135°的磨削仿真结果Fig.14 Grinding simulation results when the angle between the grinding and fiber direction is 135°

如图 15所示，夹角为 135°时，纤维束在刀具的推动作用下，发生弯曲和折断，纤维束之间有裂纹出现，缺陷扩展到工件内部，纤维断裂长度参差不齐，表面有部分凹坑，表面质量较差．磨削实验与仿真分析结果吻合较好．对应的 AE信号(图 16)大多为纤维断裂的声发射信号，与仿真结果保持一致．

图15 磨削表面电镜图像(＝135°)Fig.15 SEM image of grinding surface(＝135°)

3.5 磨削力分析

由图 17可见，磨削力随时间变化上下波动，这是由于石英纤维复合材料是由纤维、基体和界面三相构成，具有各向异性．因为纤维的剪切强度比拉压强度小，故沿着纤维端面磨削的磨削力要小于其他方向，趋于稳定阶段的 0°和 135°方向的磨削力要大于另外两个方向．在磨削过程中，基体的磨屑呈碎末状，纤维大多断成或长或短的条状．当沿着纤维端面磨削时，纤维受到剪切作用，由于纤维的剪切强度相比拉压强度较小，磨削力要小于其他方向，故纤维的端面较为平整；当沿着纤维方向磨削时，纤维主要受到磨粒的挤压、耕犁，纤维拉压强度高，故不易断裂，加工过程磨削力较大，导致加工表面参差不齐，由于界面强度低，易形成层间剥离；当夹角为 45°、135°时，纤维受到磨粒的剪切和挤压共同作用，由于界面强度更低，处于亚表面的材料由于界面的失效发生损伤，夹角为 135°时，属逆向磨削，纤维易被掀起发生断裂，并留下凹坑，加工表面质量较差．

图16 声发射频谱及小波能量分布(＝135°)Fig.16 Spectrum and wavelet energy distribution map of acoustic emission signal(＝135°)

图17 主磨削力随时间的变化Fig.17 Change of main grinding force with time

3.6 材料磨削机理分析

在石英纤维机织复合材料加工过程中，由于在复合材料磨削过程中，基体失效应力较小且其破坏能量低于纤维，导致基体先于纤维达到损伤起始准则而发生破坏，结合仿真与实验中复合材料磨削过程可以看到，基体发生压溃和拉伸断裂，由于刀具与工件之间的相互接触导致在磨粒周围形成一个应力集中区，当应力达到起始判据后，损伤开始发生，基体发生破坏，材料发生破坏，损伤发生以后，基体会沿着界面层失效而开裂．

纤维束在磨削过程中不断受到磨粒挤压、拉伸、弯曲、剪切的综合作用而发生不同的失效，磨削纤维束端面时纤维断头主要受到磨粒的剪切作用而呈平整型，而 45°和 135°时的纤维束断头受到磨粒的剪切、弯曲、挤压的复合作用发生断裂、拔出而呈阶梯型，沿着纤维长度方向磨削时纤维主要发生弯曲变形，达到抗弯强度时发生断裂，断裂长度随机分布，长短不一．

结合仿真和SEM图像可知，当纤维方向角为0°时，大量基体破碎和界面失效发生，基体由于到达最大主应力而发生碎裂，界面由于受到弯曲作用产生裂纹，材料此时的裂纹起始是由于基体最大主应力水平和界面抗弯和抗压强度主导的，裂纹扩展沿着界面开裂．沿着纤维端面磨削时，由于界面剪切强度较低，所以裂纹沿着裂纹开裂并发生扩展．当磨削方向与纤维方向夹角为 45°和 135°时，磨削表面的基体破碎比较严重，从仿真图像可以看出，处于亚表面的界面损伤较严重，界面脱黏被基体裂纹连接起来形成一条贯穿裂纹，裂纹的起始主要受基体最大主应力水平和界面剪切强度影响，裂纹扩展沿着纤维和基体间的界面开裂．

磨削过程中，机械应力可分为挤压应力和切削应力．磨粒向前移动，使表面沿切削运动方向受到压缩作用，而在其垂直方向受到拉伸作用，从而导致切削运动方向产生残余拉应力，而在其垂直方向产生残余压应力．这是假设磨粒尖端绝对锋利下的分析结果．实际上，由于磨粒存在磨损和崩刃的情况，使磨粒刃前方和下方的材料受压，切削引起的残余应力存在拉、压应力两种可能，其数值小于挤压作用引起的残余应力．

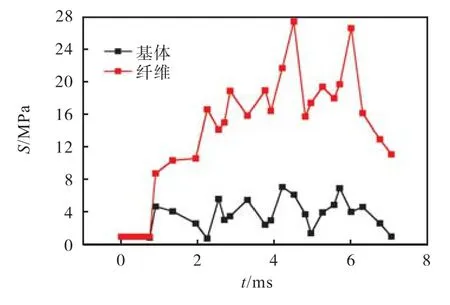
图18 纤维和基体代表节点的应力-时间曲线Fig.18 Stress-time curve of representative nodes of fiber and matrix

图 18所示为沿着纤维端面磨削的代表点A、B(如图 5所示)的应力随加工时间的变化，与纤维相比基体始终处于一个较高的正压力值，表明残余应力的作用使纤维受到压缩．从图 5应力云图中可以看出，纤维端部相比其他位置应力值最大，尤其在纤维与基体的交界面处．结合应力云图和节点应力曲线，基体的应力值是一个低平值并出现负值，表面残余应力在一部分时间里使基体受到拉伸作用，加工过后基体的残余应力处于一个较小值．

4 结 论

本文主要的内容是对石英纤维复合材料磨削过程进行仿真分析，基于简化假设的条件下建立了与实际较相符的几何模型．利用商业有限元软件进行材料的磨削仿真，力学模型中，纤维采用部分Hashin失效准则，基体是各向同性材料采用最大应力准则．最后通过磨削实验与仿真结果相对比，进行经验总结而得出以下结论．

(1) 在磨削过程中，复合材料会发生纤维断裂、纤维拔出、基体破碎以及界面脱黏等，断裂起始主要是由基体最大主应力和界面强度主导的，产生的裂纹沿着界面扩展．

(2) 纤维方向是影响复合材料磨削加工质量的重要因素，沿着纤维端面的加工质量较好，夹角为 0°和 45°时次之，135°时最差，纤维受剪切时的加工表面质量相比纤维受拉压发生断裂后的表面质量好．

(3) 实验与仿真结果基本相符，验证了细观模型中纤维组分借鉴部分 Hashin准则、基体组分采用最大应力准则、界面层采用二次应力准则及 B-K准则的本构模型是适用的．

(4) 纤维束材料在不同磨削方向时由于受到不同磨粒的剪切、弯曲、挤压和耕犁的综合作用，断头分别呈现平整形、阶梯形、随机性分布的状态．

(5) 加工后纤维的残余应力相比基体的残余应力大，在端面磨削中，残余应力使纤维受到压缩作用且纤维端部应力值最大．

[1] 陈凡军，罗 军，陈 革.三维角联锁机织复合材料有限元分析[J].东华大学学报：自然科学版，2015，41(1)：28-31.

Chen Fanjun，Luo Jun，Chen Ge.Finite element analysis on 3D angle interlock woven composite[J].Journal of Donghua University：Natural Science，2015，41(1)：28-31(in Chinese).

[2] 董伟锋，张建钟，肖 军.2.5D机织复合材料弹性性能的有限元分析[J].材料工程，2009(增2)：9-14.

Dong Weifeng，Zhang Jianzhong，Xiao Jun.Finite element analysis of the elastic properties of 2.5D woven composites[J].Journal of Materials Engineering，2009(Suppl 2)：9-14(in Chinese).

[3] 姚 瑶，金利民.层层接结三维角联锁机织复合材料的三点弯曲疲劳破坏[J].纤维复合材料，2014(2)：41-44.

Yao Yao，Jin Limin.Fatigue damage of layer-to-layer three-dimensional angle-interlock woven composite undergoing three-point bending loading[J].Fiber Composites，2014(2)：41-44(in Chinese).

[4] Ko F，Du G W.Processing of textile performs[C]//Advanced Composites Manufacturing.New York：New York John Wiley & Sons，Inc，1997：187-189.

[5] Pochiraju K，Chou T W.Three-dimensionally woven and braided composites-1：A model for anisotropic stiffness prediction[J].Polymer Composites，1999，20(4)：565-580.

[6] Wang Yuguo，Ding Chao，Lin Bin.FEM simulation of single-grit grinding on a 2.5D woven composite[J].Transactions of Tianjin University，2017，23(1)：1-9.

[7] 路 冬，李志凯，融亦鸣，等.基于宏观各向异性碳纤维增强树脂基复合材料的切削仿真[J].复合材料学报，2014，31(3)：584-590.

Lu Dong，Li Zhikai，Rong Yiming，et al.Cutting simulation of carbon fiber reinforced resin matrix composite material based on macroscopic anisotropy[J].Acta Materiae Compositae Sinica，2014，31(3)：584-590(in Chinese).

[8] 高汉卿，贾振元，王福吉，等.基于细观仿真建模的CFRP细观破坏[J].复合材料学报，2016，33(4)：758-767.

Gao Hanqing，Jia Zhenyuan，Wang Fuji，et al.Mesoscopic failure of CFRP based on mesoscopic simulation modeling[J].Acta Materiae Compositae Sinica，2016，33(4)：758-767(in Chinese).

[9] Abena A，Soo S L，Essa K.Modelling the orthogonal cutting of UD-CFRP composites：Development of a novel cohesive zone model[J].Composite Structures，2017，168：65-83.

[10] Solani X，Santinuste C.Influence of tool geometry and numerical parameters when modeling orthogonal cutting of LERP composites[J].Composites，2011，42：1205-1216.

[11] Rao G，Mahajan P，Bhatnagar N.Three-dimensional macro-mechanical finite element model for machining of unidirectional-fiber reinforced polymer composites[J].Materials Science and Engineering A，2008，498：142-149.

[12] Mahdi M，Zhang L C.An adaptive three dimensional finite element algorithm for the orthogonal cutting of composite materials[J].Journal of Materials Processing Technology，2001，113(1)：368-372.

[13] 李巾锭，任成祖，吕 哲，等.单颗粒金刚石平面磨削C/SiC复合材料的有限元仿真[J].材料科学与工程学报，2014，32(5)：686-689.

Li Jinding，Ren Chengzu，Lü Ze，et al.Finite element simulation of single diamond abrasive surface grinding C/SiC[J].Journal of Materials Science & Engineering，2014，32(5)：686-689(in Chinese).

[14] Woo Sung-Choong，Kim Tae-Won.High strain-rate failure in carbon/Kevlar hybrid woven composites via a novel SHPB-AE coupled test[J].Composites Part B，2016，97：317-328.

[15] Ely T M，Hill E.Longitudinal splitting and fiber breakage characterization in graphite epoxy using acoustic emission data[J].Materials Evaluation，1995，53(2)：288-294.

[16] Gutkin R，Green C J，Vangrattanachai S，et al.On acoustic emission for failure investigation in CFRP：Pattern recognition and peak frequency analyses[J].Mechanical System and Signal Processing，2011，25(4)：1393-1407.

[17] 冯古雨，曹海建，周红涛，等.三维机织复合材料单胞模型各向异性的有限元分析[J].玻璃钢/复合材料，2017(8)：48-52.

Feng Guyu，Cao Haijian，Zhou Hongtao，et al.Finite element analysis on anisotropy of 3D composite unit-cell model[J].Fiber Reinforced Plastic/Composites，2017(8)：48-52(in Chinese).

[18] 关天茹.2.5D编织石英/SiO2陶瓷基复合材料细观模型构建与实验验证[D].南京：南京航空航天大学，2012.

Guan Tianru.Microgeometry and Mechanical Model and Experimental Study of 2.5D Braided Quartz/SiO2Ceramic Matrix Composites[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2012(in Chinese).

[19] 郭芳芳，肖建章.基于三相微观结构的纤维复合材料切削仿真研究[J].工具技术，2017，51(6)：26-30.

Guo Fangfang，Xiao Jianzhang.Study on cutting simulation of fiber reinforced composite materials based on three phase microstructure[J].Tool Engineering，2017，51(6)：26-30(in Chinese).

[20] 韩文钦.复合材料层合板损伤演化的实验和数值分析[D].镇江：江苏大学，2017.

Han Wenqin.Experimental and Numerical Analysis on Damage Evolution of Composite Laminates[D].Zhenjiang：Jiangsu University，2017(in Chinese).